# Seznam známek
znamky = [1, 2, 1, 3, 2, 1]
print(znamky)[1, 2, 1, 3, 2, 1]V této kapitole se naučíte:
V matematice často pracujeme s více čísly najednou. V Pythonu k tomu slouží seznamy (anglicky lists).
# Seznam známek
znamky = [1, 2, 1, 3, 2, 1]
print(znamky)[1, 2, 1, 3, 2, 1]# Seznam teplot v týdnu
teploty = [15.2, 17.8, 16.5, 14.0, 13.2, 18.4, 20.1]
print(teploty)[15.2, 17.8, 16.5, 14.0, 13.2, 18.4, 20.1]Každý prvek má svůj index (pozici). Pozor: indexujeme od nuly!
ovoce = ["jablko", "hruška", "banán", "pomeranč"]
print(ovoce[0]) # První prvek
print(ovoce[1]) # Druhý prvek
print(ovoce[-1]) # Poslední prvekjablko
hruška
pomeranč# Můžeme měnit hodnoty
ovoce[1] = "třešeň"
print(ovoce)['jablko', 'třešeň', 'banán', 'pomeranč']cisla = [1, 2, 3, 4, 5]
# Délka seznamu
print("Délka:", len(cisla))
# Součet všech prvků
print("Součet:", sum(cisla))
# Minimum a maximum
print("Minimum:", min(cisla))
print("Maximum:", max(cisla))Délka: 5
Součet: 15
Minimum: 1
Maximum: 5# Přidání prvku na konec
cisla.append(6)
print(cisla)[1, 2, 3, 4, 5, 6]# Spojení dvou seznamů
seznam1 = [1, 2, 3]
seznam2 = [4, 5, 6]
spojeny = seznam1 + seznam2
print(spojeny)[1, 2, 3, 4, 5, 6]Průměr seznamu čísel vypočítáme jako sum(seznam) / len(seznam).
Cykly nám umožňují opakovat kód pro každý prvek seznamu nebo určitý počet opakování.
# Projdeme každý prvek seznamu
barvy = ["červená", "zelená", "modrá"]
for barva in barvy:
print("Moje oblíbená barva je:", barva)Moje oblíbená barva je: červená
Moje oblíbená barva je: zelená
Moje oblíbená barva je: modráV Pythonu se bloky kódu označují odsazením (4 mezery nebo 1 tabulátor). Vše, co je odsazené za for, patří do cyklu.
# Výpočet průměru pomocí cyklu
znamky = [1, 2, 1, 3, 2, 1, 2]
soucet = 0
for znamka in znamky:
soucet = soucet + znamka
prumer = soucet / len(znamky)
print("Průměrná známka:", round(prumer, 2))Průměrná známka: 1.71Když chceme opakovat něco určitý počet krát, použijeme range():
# Vytiskne čísla 0 až 4
for i in range(5):
print(i)0
1
2
3
4# range(start, stop) - od start do stop-1
for i in range(1, 6):
print(i)1
2
3
4
5# Výpočet 5! (faktoriál)
faktorial = 1
for i in range(1, 6):
faktorial = faktorial * i
print(f"{i}! = {faktorial}")1! = 1
2! = 2
3! = 6
4! = 24
5! = 120Zápis f"text {proměnná}" je tzv. f-string – umožňuje vkládat proměnné přímo do textu.
Podmínky umožňují programu dělat různé věci v závislosti na situaci.
vek = 16
if vek >= 18:
print("Jste plnoletý/á")
else:
print("Jste nezletilý/á")Jste nezletilý/á| Operátor | Význam |
|---|---|
== |
rovná se |
!= |
nerovná se |
< |
menší než |
> |
větší než |
<= |
menší nebo rovno |
>= |
větší nebo rovno |
cislo = 7
if cislo > 0:
print("Číslo je kladné")
elif cislo < 0:
print("Číslo je záporné")
else:
print("Číslo je nula")Číslo je kladnévek = 25
ma_ridicak = True
# AND - obě podmínky musí platit
if vek >= 18 and ma_ridicak:
print("Může řídit auto")
# OR - stačí jedna podmínka
teplota = 35
if teplota < 0 or teplota > 30:
print("Extrémní teplota!")
# NOT - negace
je_dest = False
if not je_dest:
print("Neprší, můžeme ven!")Může řídit auto
Extrémní teplota!
Neprší, můžeme ven!# Najdeme všechna sudá čísla
cisla = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print("Sudá čísla:")
for cislo in cisla:
if cislo % 2 == 0: # Zbytek po dělení 2 je 0
print(cislo)Sudá čísla:
2
4
6
8
10Funkce jsou pojmenované bloky kódu, které můžeme opakovaně používat.
# Definice funkce
def pozdrav(jmeno):
print(f"Ahoj, {jmeno}!")
# Volání funkce
pozdrav("Anna")
pozdrav("Petr")Ahoj, Anna!
Ahoj, Petr!def druha_mocnina(x):
return x ** 2
vysledek = druha_mocnina(5)
print("5² =", vysledek)5² = 25# Funkce pro výpočet obsahu kruhu
def obsah_kruhu(polomer):
pi = 3.14159
return pi * polomer ** 2
print("Obsah kruhu s r=3:", round(obsah_kruhu(3), 2))
print("Obsah kruhu s r=5:", round(obsah_kruhu(5), 2))Obsah kruhu s r=3: 28.27
Obsah kruhu s r=5: 78.54def objem_kvadru(delka, sirka, vyska):
return delka * sirka * vyska
print("Objem:", objem_kvadru(2, 3, 4))Objem: 24def mocnina(zaklad, exponent=2):
return zaklad ** exponent
print("3² =", mocnina(3)) # Použije výchozí exponent 2
print("3³ =", mocnina(3, 3)) # Přepíše výchozí hodnotu3² = 9
3³ = 27NumPy (Numerical Python) je knihovna pro efektivní práci s čísly a poli. Je základem pro vědecké výpočty v Pythonu.
# Instalace (v terminálu)
pip install numpyimport numpy as np # Importujeme a zkrátíme název na "np"# Python seznam
import numpy as np
python_seznam = [1, 2, 3, 4, 5]
# NumPy pole
numpy_pole = np.array([1, 2, 3, 4, 5])
print("Python seznam:", python_seznam)
print("NumPy pole:", numpy_pole)Python seznam: [1, 2, 3, 4, 5]
NumPy pole: [1 2 3 4 5]Hlavní výhoda NumPy: operace se aplikují na všechny prvky najednou!
import numpy as np
cisla = np.array([1, 2, 3, 4, 5])
# Přičtení ke každému prvku
print("+ 10:", cisla + 10)
# Vynásobení každého prvku
print("× 2:", cisla * 2)
# Druhá mocnina každého prvku
print("²:", cisla ** 2)+ 10: [11 12 13 14 15]
× 2: [ 2 4 6 8 10]
²: [ 1 4 9 16 25]# Porovnejte s Python seznamem
python_seznam = [1, 2, 3, 4, 5]
# python_seznam + 10 # Toto by způsobilo chybu!
# python_seznam * 2 # Toto by zdvojilo seznam, ne hodnoty!
print("Python seznam * 2:", python_seznam * 2)Python seznam * 2: [1, 2, 3, 4, 5, 1, 2, 3, 4, 5]import numpy as np
data = np.array([23, 45, 12, 67, 34, 89, 21])
print("Součet:", np.sum(data))
print("Průměr:", np.mean(data))
print("Minimum:", np.min(data))
print("Maximum:", np.max(data))
print("Směrodatná odchylka:", round(np.std(data), 2))Součet: 291
Průměr: 41.57142857142857
Minimum: 12
Maximum: 89
Směrodatná odchylka: 25.66# Pole nul
import numpy as np
nuly = np.zeros(5)
print("Nuly:", nuly)
# Pole jedniček
jednicky = np.ones(5)
print("Jedničky:", jednicky)
# Rovnoměrně rozložená čísla
rozsah = np.linspace(0, 10, 5) # 5 čísel od 0 do 10
print("Linspace:", rozsah)
# Celá čísla
cela = np.arange(0, 10, 2) # Od 0 do 10, krok 2
print("Arange:", cela)Nuly: [0. 0. 0. 0. 0.]
Jedničky: [1. 1. 1. 1. 1.]
Linspace: [ 0. 2.5 5. 7.5 10. ]
Arange: [0 2 4 6 8]Matplotlib je knihovna pro vytváření grafů a vizualizací.
# Instalace (v terminálu)
pip install matplotlibimport matplotlib.pyplot as plt# Data
import matplotlib.pyplot as plt
x = [1, 2, 3, 4, 5]
y = [1, 4, 9, 16, 25]
# Vytvoření grafu
plt.figure(figsize=(8, 5))
plt.plot(x, y)
plt.xlabel("x")
plt.ylabel("y = x²")
plt.title("Graf funkce y = x²")
plt.grid(True)
plt.show()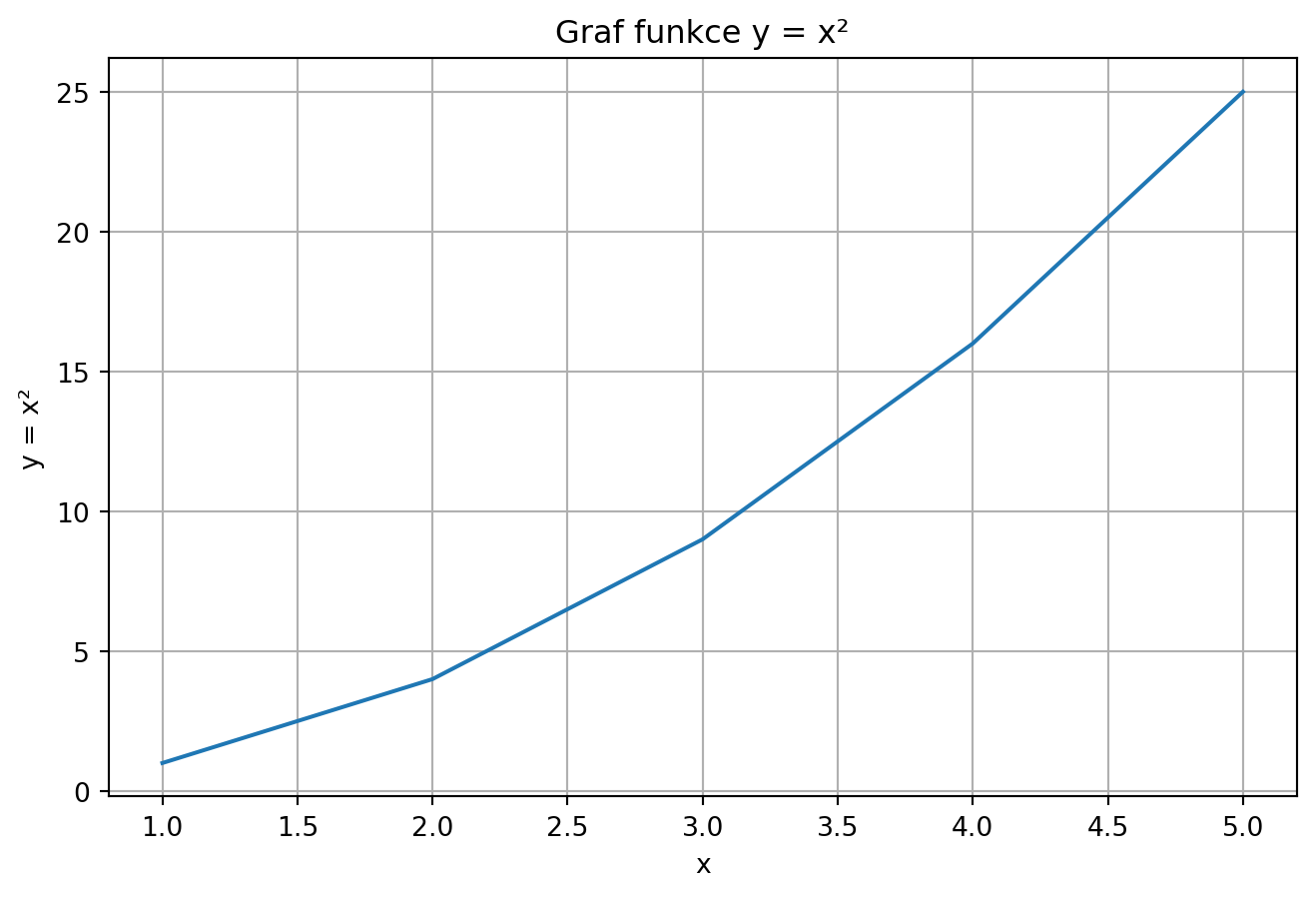
# Vytvoříme 100 bodů od 0 do 2π
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2 * np.pi, 100)
# Vypočítáme sinus a kosinus
y_sin = np.sin(x)
y_cos = np.cos(x)
# Nakreslíme
plt.figure(figsize=(10, 5))
plt.plot(x, y_sin, label="sin(x)")
plt.plot(x, y_cos, label="cos(x)")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Goniometrické funkce")
plt.legend() # Zobrazí legendu
plt.grid(True)
plt.show()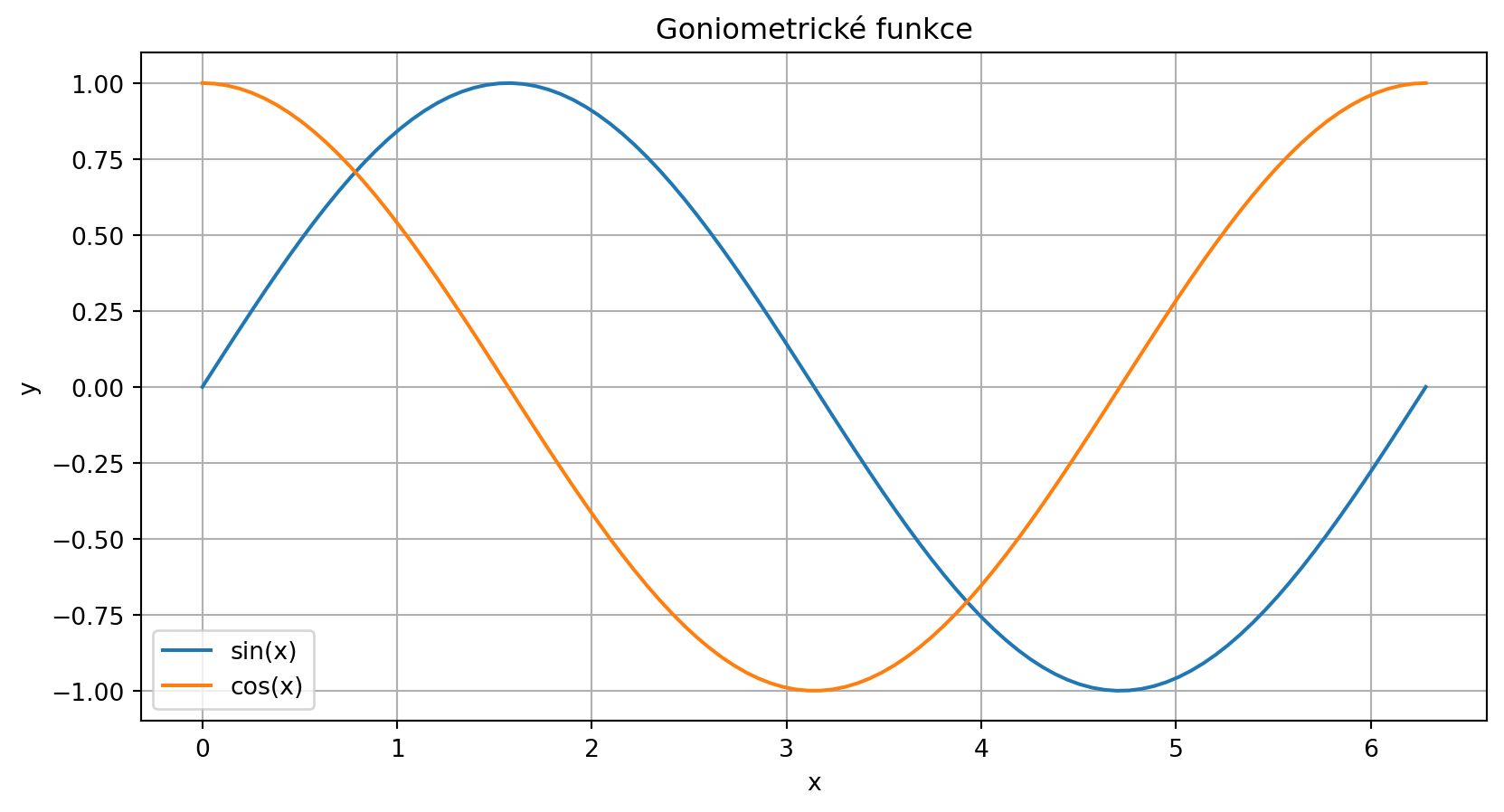
# Náhodná data
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42) # Pro reprodukovatelnost
x = np.random.randn(50) # 50 náhodných čísel
y = x + np.random.randn(50) * 0.5 # y závisí na x + šum
plt.figure(figsize=(8, 5))
plt.scatter(x, y, alpha=0.7)
plt.xlabel("x")
plt.ylabel("y")
plt.title("Bodový graf")
plt.grid(True)
plt.show()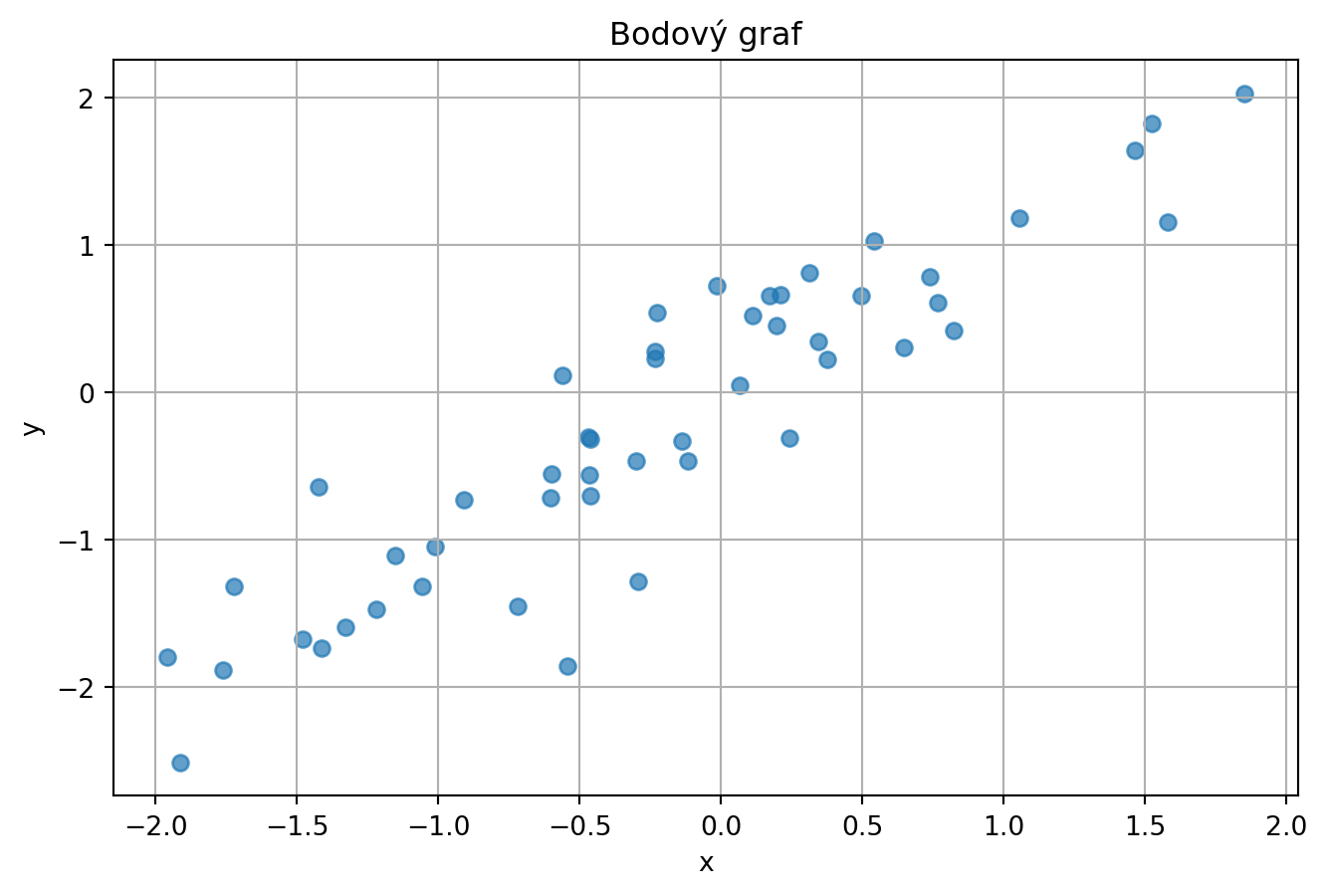
# Data - známky ve třídě
import matplotlib.pyplot as plt
znamky = [1, 1, 2, 1, 3, 2, 2, 1, 4, 2, 3, 1, 2, 2, 1, 3, 2, 1, 2, 5]
plt.figure(figsize=(8, 5))
plt.hist(znamky, bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5],
edgecolor='black', alpha=0.7)
plt.xlabel("Známka")
plt.ylabel("Počet")
plt.title("Rozložení známek ve třídě")
plt.xticks([1, 2, 3, 4, 5])
plt.grid(True, alpha=0.3)
plt.show()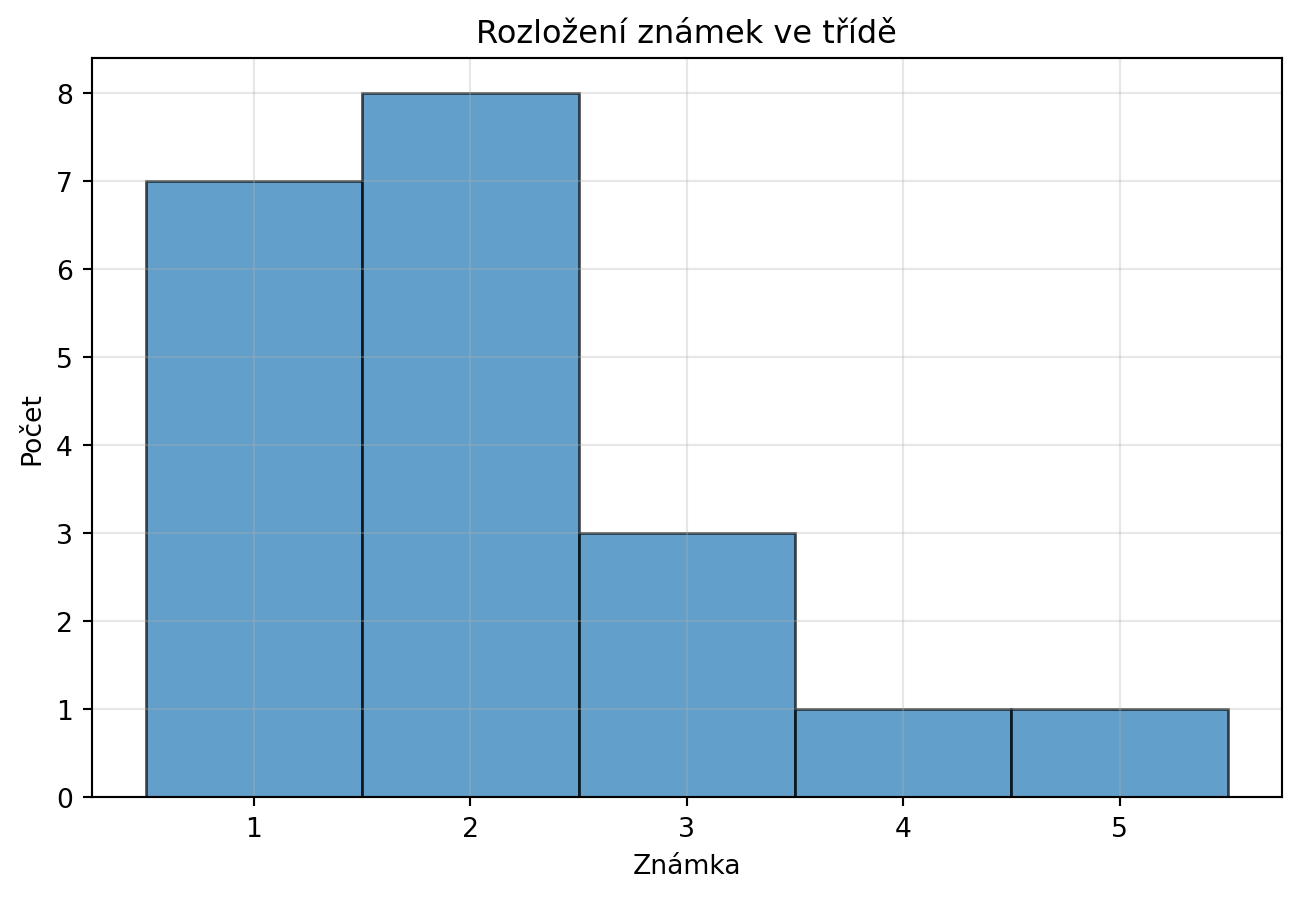
def vypocti_prumer(seznam):
"""Vypočítá průměr hodnot v seznamu."""
return sum(seznam) / len(seznam)
znamky_matematika = [1, 2, 1, 3, 2]
znamky_fyzika = [2, 2, 3, 2, 1]
print("Průměr z matematiky:", round(vypocti_prumer(znamky_matematika), 2))
print("Průměr z fyziky:", round(vypocti_prumer(znamky_fyzika), 2))Průměr z matematiky: 1.8
Průměr z fyziky: 2.0def najdi_maximum(cisla):
"""Najde největší číslo v seznamu."""
maximum = cisla[0] # Začneme s prvním číslem
for cislo in cisla:
if cislo > maximum:
maximum = cislo
return maximum
teploty = [15, 18, 22, 19, 25, 23, 20]
print("Nejvyšší teplota:", najdi_maximum(teploty), "°C")Nejvyšší teplota: 25 °Cdef faktorial(n):
"""Vypočítá n! = 1 × 2 × 3 × ... × n"""
vysledek = 1
for i in range(1, n + 1):
vysledek = vysledek * i
return vysledek
for n in range(1, 8):
print(f"{n}! = {faktorial(n)}")1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040def fibonacci(n):
"""Vrátí prvních n členů Fibonacciho posloupnosti."""
if n <= 0:
return []
elif n == 1:
return [0]
fib = [0, 1]
for i in range(2, n):
dalsi = fib[i-1] + fib[i-2]
fib.append(dalsi)
return fib
print("Prvních 10 Fibonacciho čísel:")
print(fibonacci(10))Prvních 10 Fibonacciho čísel:
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**2 - 4*x + 3
x = np.linspace(-1, 5, 100)
y = f(x)
plt.figure(figsize=(8, 5))
plt.plot(x, y, 'b-', linewidth=2)
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.xlabel("x")
plt.ylabel("y")
plt.title("f(x) = x² - 4x + 3")
plt.grid(True, alpha=0.3)
plt.show()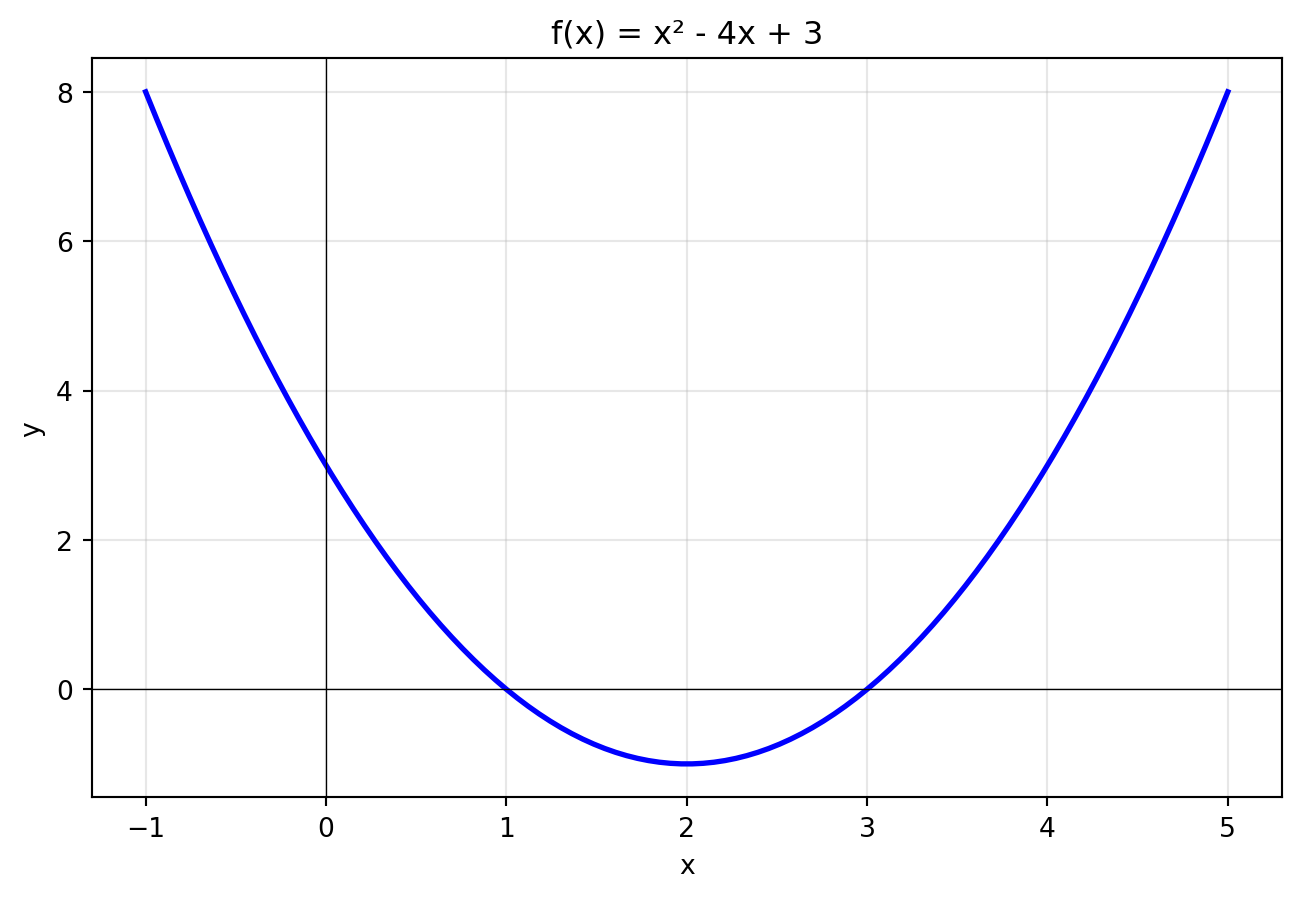
Napište funkci soucet(seznam), která vrátí součet všech prvků seznamu bez použití funkce sum().
Test: soucet([1, 2, 3, 4, 5]) by mělo vrátit 15
def soucet(seznam):
vysledek = 0
for prvek in seznam:
vysledek = vysledek + prvek
return vysledekNapište funkci pocet_sudych(cisla), která vrátí počet sudých čísel v seznamu.
Test: pocet_sudych([1, 2, 3, 4, 5, 6]) by mělo vrátit 3
def pocet_sudych(cisla):
pocet = 0
for cislo in cisla:
if cislo % 2 == 0:
pocet = pocet + 1
return pocetNapište funkci fahrenheit_na_celsius(f) a použijte ji pro převod seznamu teplot [32, 68, 86, 104] °F na °C.
Vzorec: C = (F - 32) × 5/9
def fahrenheit_na_celsius(f):
return (f - 32) * 5/9
teploty_f = [32, 68, 86, 104]
for f in teploty_f:
c = fahrenheit_na_celsius(f)
print(f"{f}°F = {round(c, 1)}°C")Nakreslete do jednoho grafu funkce y = x, y = x² a y = x³ pro x od -2 do 2.
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 2, 100)
plt.figure(figsize=(8, 6))
plt.plot(x, x, label="y = x")
plt.plot(x, x**2, label="y = x²")
plt.plot(x, x**3, label="y = x³")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Porovnání funkcí")
plt.legend()
plt.grid(True)
plt.show()Vytvořte funkci statistika(data), která pro zadaný NumPy pole vrátí slovník s klíči min, max, prumer, suma.
import numpy as np
def statistika(data):
return {
'min': np.min(data),
'max': np.max(data),
'prumer': np.mean(data),
'suma': np.sum(data)
}
cisla = np.array([10, 20, 30, 40, 50])
vysledek = statistika(cisla)
print(vysledek)[1, 2, 3]) ukládají více hodnot, indexujeme od 0for x in seznam:if, elif, else) umožňují rozhodovánídef nazev():) vytváří znovupoužitelné bloky kóduimport numpy as npimport matplotlib.pyplot as pltNyní máte všechny základní nástroje Pythonu, které budeme potřebovat. V další části se ponoříme do matematiky – začneme souřadnicovým systémem a funkcemi!