# Hledání minima {#sec-hledani-minima}
## Motivace: Proč hledáme minimum?
Trénování neuronové sítě je v jádru **optimalizační problém**. Máme:
1. **Model** s parametry (váhy, biasy)
2. **Loss funkci**, která měří, jak špatně model predikuje
3. **Cíl**: najít parametry, které minimalizují loss
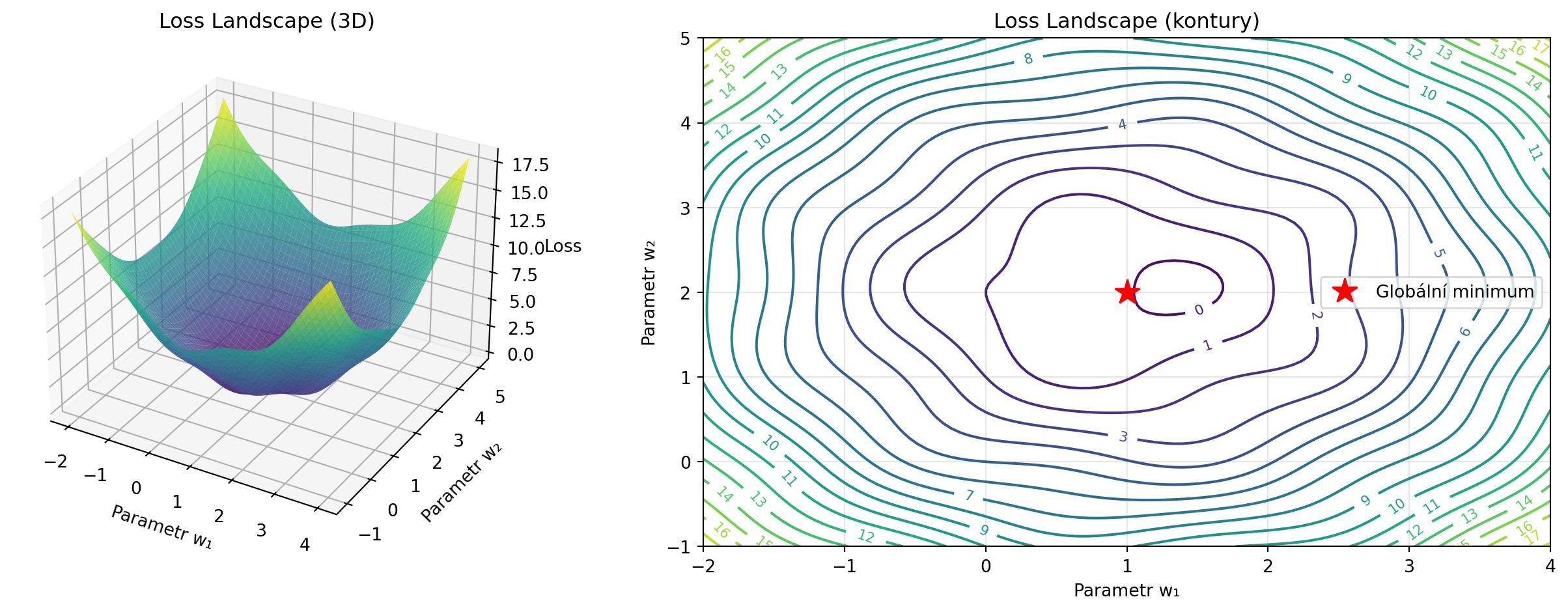
Představte si loss funkci jako krajinu - hory a údolí. Chceme najít nejnižší bod (globální minimum). Tato kapitola vysvětlí základní koncepty optimalizace, které jsou klíčové pro pochopení, jak se neuronové sítě učí.
```{python}
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Vizualizace loss landscape
def loss_landscape(x, y):
return (x - 1)**2 + (y - 2)**2 + 0.5 * np.sin(3*x) * np.cos(3*y)
x = np.linspace(-2, 4, 100)
y = np.linspace(-1, 5, 100)
X, Y = np.meshgrid(x, y)
Z = loss_landscape(X, Y)
fig = plt.figure(figsize=(14, 5))
# 3D pohled
ax1 = fig.add_subplot(121, projection='3d')
ax1.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
ax1.set_xlabel('Parametr w₁')
ax1.set_ylabel('Parametr w₂')
ax1.set_zlabel('Loss')
ax1.set_title('Loss Landscape (3D)')
# Kontury
ax2 = fig.add_subplot(122)
contour = ax2.contour(X, Y, Z, levels=20, cmap='viridis')
ax2.clabel(contour, inline=True, fontsize=8)
ax2.plot(1, 2, 'r*', markersize=15, label='Globální minimum')
ax2.set_xlabel('Parametr w₁')
ax2.set_ylabel('Parametr w₂')
ax2.set_title('Loss Landscape (kontury)')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
## Co je optimalizace?
::: {.callout-note}
## Definice: Optimalizační problém
**Minimalizace**: Najít $\mathbf{x}^*$ takové, že:
$$\mathbf{x}^* = \arg\min_{\mathbf{x}} f(\mathbf{x})$$
kde $f$ je **účelová funkce** (objective function), v ML typicky loss funkce.
:::
V kontextu neuronových sítí:
- $\mathbf{x}$ = všechny váhy a biasy sítě (může jich být miliony!)
- $f(\mathbf{x})$ = průměrná loss na trénovacích datech
```{python}
# Jednoduchý příklad: Kvadratická funkce
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return (x - 3)**2 + 1
x = np.linspace(-2, 8, 100)
plt.figure(figsize=(10, 5))
plt.plot(x, f(x), 'b-', lw=2, label='f(x) = (x-3)² + 1')
plt.axvline(x=3, color='red', linestyle='--', label='Minimum při x=3')
plt.scatter([3], [1], color='red', s=100, zorder=5)
plt.xlabel('x')
plt.ylabel('f(x)')
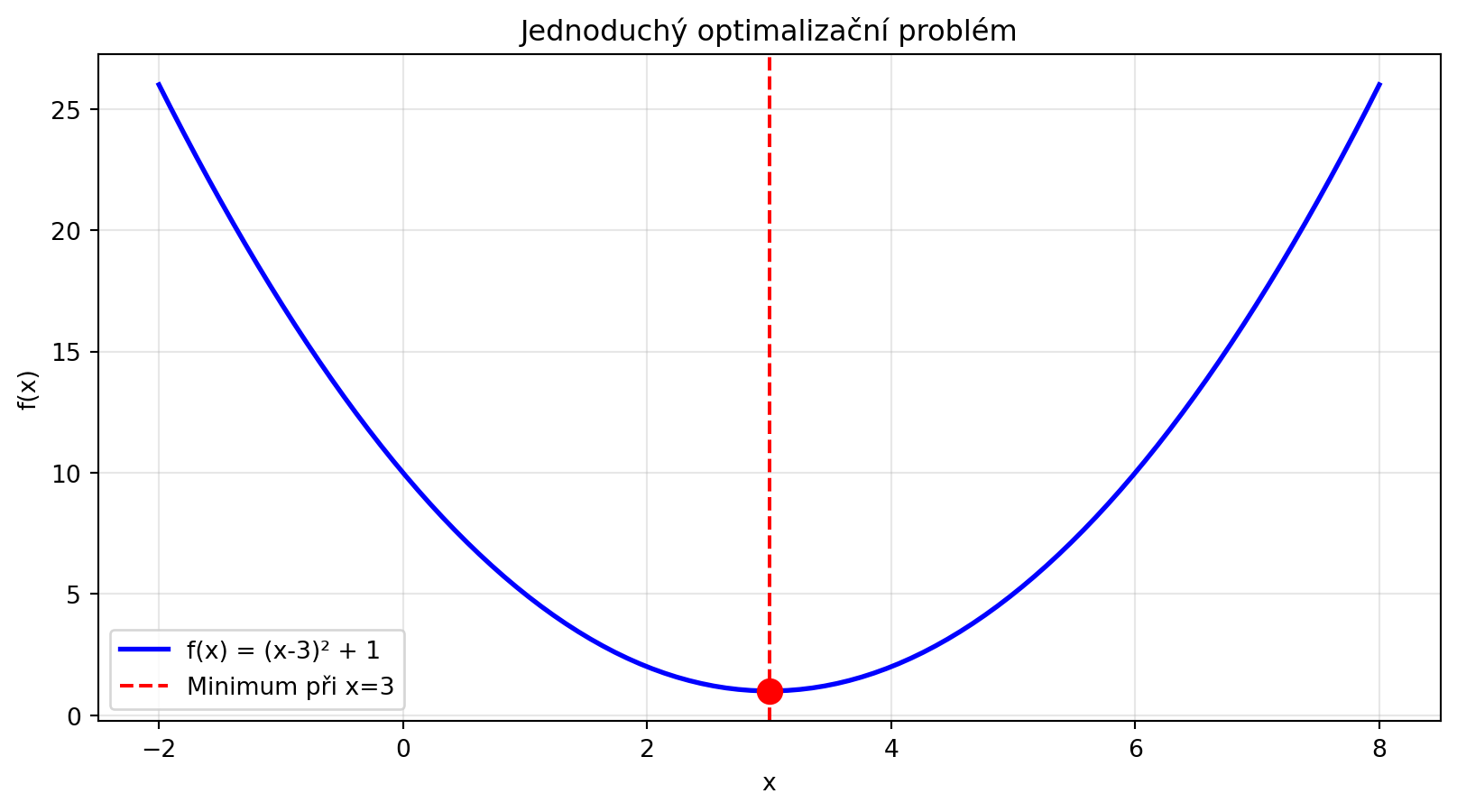
plt.title('Jednoduchý optimalizační problém')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
print("Minimum funkce f(x) = (x-3)² + 1:")
print(f" x* = 3")
print(f" f(x*) = 1")
```
## Lokální vs globální minimum
::: {.callout-warning}
## Důležitý rozdíl
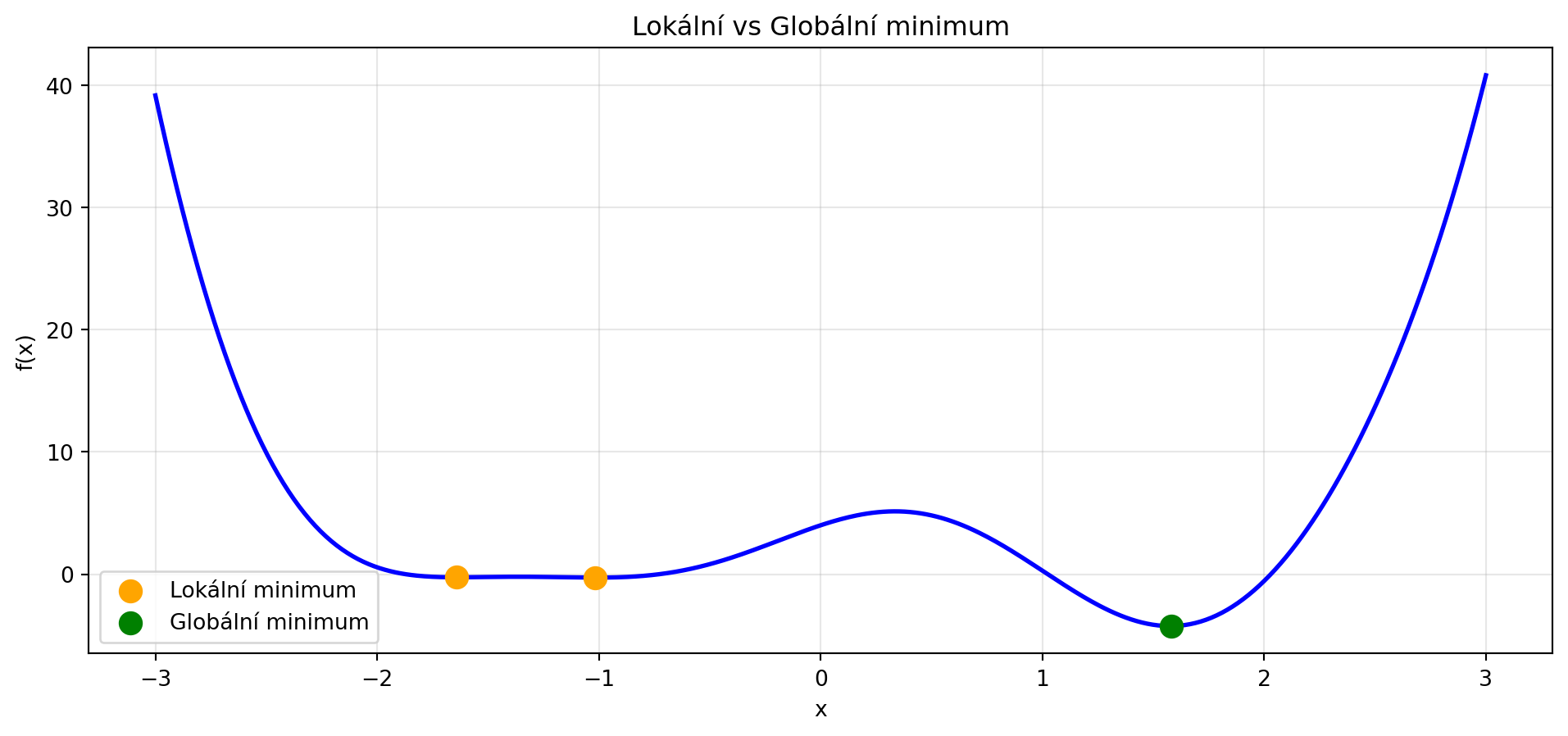
- **Globální minimum**: Nejnižší bod celé funkce
- **Lokální minimum**: Nejnižší bod v okolí (ale ne nutně celkově nejnižší)
V hlubokém učení často končíme v lokálním minimu, ale to může být dostatečně dobré!
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
def f_complex(x):
return x**4 - 5*x**2 + 4 + 2*np.sin(3*x)
x = np.linspace(-3, 3, 500)
plt.figure(figsize=(12, 5))
plt.plot(x, f_complex(x), 'b-', lw=2)
# Najdeme lokální minima numericky (bez scipy)
def find_local_minima(y, order=10):
"""Najde indexy lokálních minim."""
minima = []
for i in range(order, len(y) - order):
if all(y[i] <= y[i-j] for j in range(1, order+1)) and \
all(y[i] <= y[i+j] for j in range(1, order+1)):
minima.append(i)
return np.array(minima)
y = f_complex(x)
local_min_idx = find_local_minima(y, order=10)
for i, idx in enumerate(local_min_idx):
color = 'green' if y[idx] == min(y[local_min_idx]) else 'orange'
label = 'Globální minimum' if color == 'green' else 'Lokální minimum'
if i > 0 and color == 'orange':
label = None
plt.scatter([x[idx]], [y[idx]], color=color, s=100, zorder=5, label=label)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Lokální vs Globální minimum')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
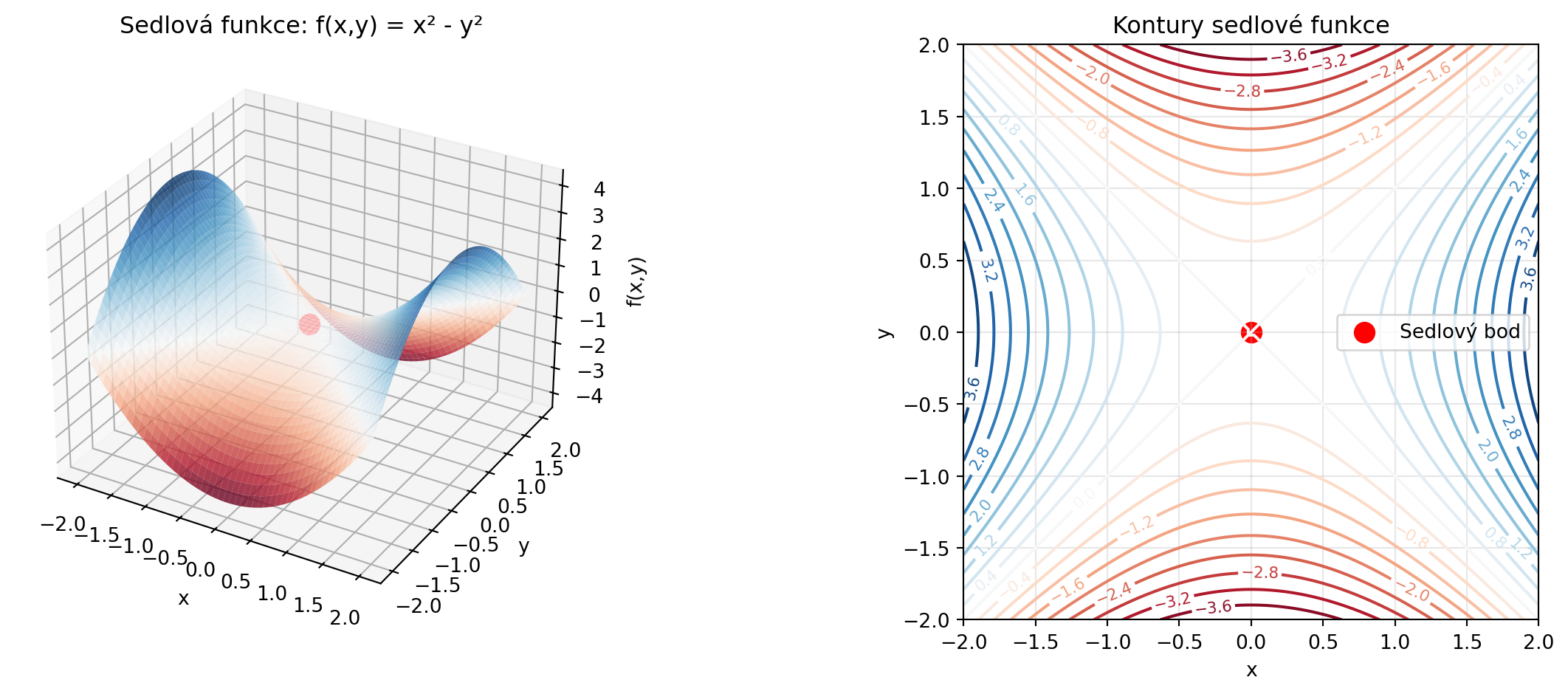
### Sedlové body
V mnoha dimenzích existují také **sedlové body** - místa, kde je gradient nulový, ale nejsou to minima:
```{python}
import numpy as np
import matplotlib.pyplot as plt
def sedlova_funkce(x, y):
return x**2 - y**2
x = np.linspace(-2, 2, 100)
y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x, y)
Z = sedlova_funkce(X, Y)
fig = plt.figure(figsize=(14, 5))
# 3D
ax1 = fig.add_subplot(121, projection='3d')
ax1.plot_surface(X, Y, Z, cmap='RdBu', alpha=0.8)
ax1.scatter([0], [0], [0], color='red', s=100, label='Sedlový bod')
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.set_zlabel('f(x,y)')
ax1.set_title('Sedlová funkce: f(x,y) = x² - y²')
# Kontury
ax2 = fig.add_subplot(122)
contour = ax2.contour(X, Y, Z, levels=20, cmap='RdBu')
ax2.clabel(contour, inline=True, fontsize=8)
ax2.scatter([0], [0], color='red', s=100, label='Sedlový bod')
ax2.set_xlabel('x')
ax2.set_ylabel('y')
ax2.set_title('Kontury sedlové funkce')
ax2.legend()
ax2.set_aspect('equal')
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("V sedlovém bodě (0, 0):")
print(" Gradient = (0, 0) - vypadá jako minimum")
print(" Ale ve směru y funkce klesá!")
```
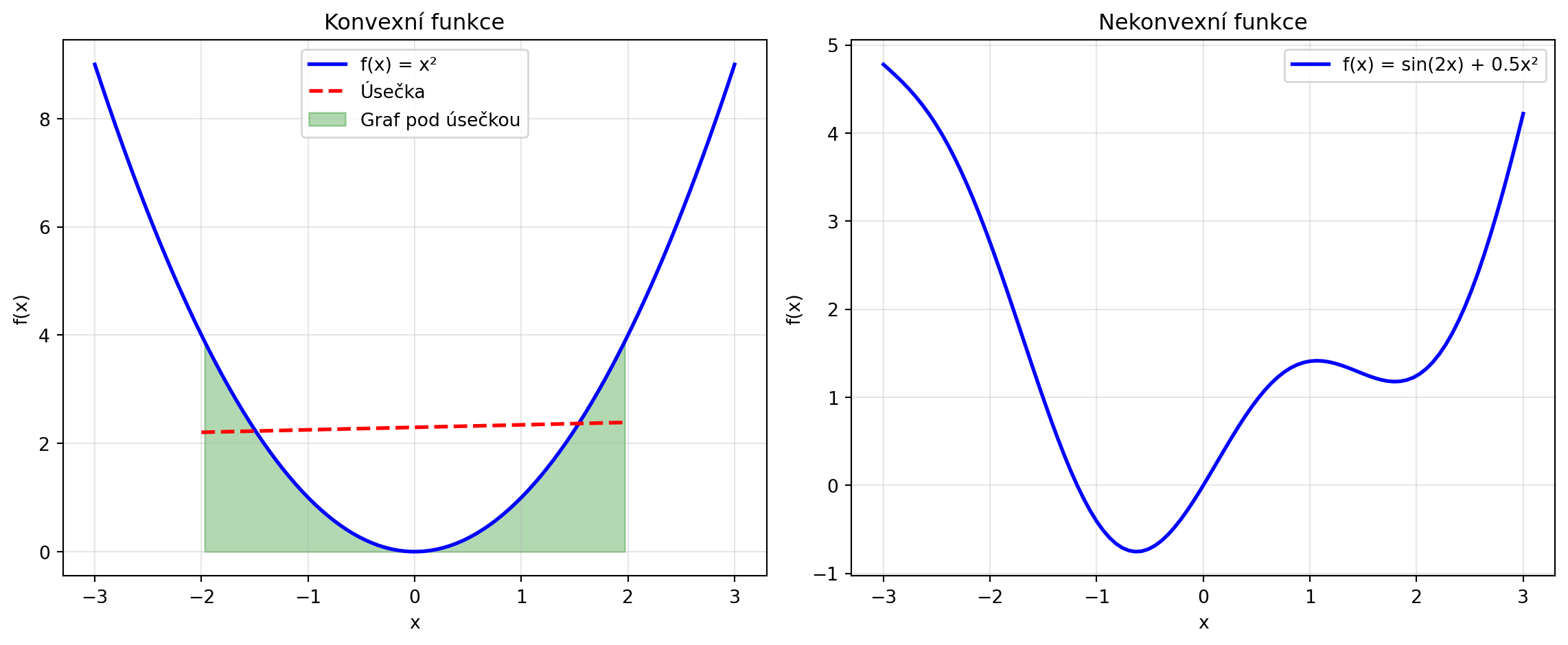
## Konvexní funkce
Některé funkce mají speciální vlastnost - jsou **konvexní**. Pro konvexní funkce platí:
- Každé lokální minimum je zároveň globální
- Optimalizace je "snadná" - gradient descent vždy konverguje
::: {.callout-note}
## Definice: Konvexní funkce
Funkce $f$ je **konvexní**, pokud pro libovolné body $x_1, x_2$ a $\lambda \in [0, 1]$:
$$f(\lambda x_1 + (1-\lambda) x_2) \leq \lambda f(x_1) + (1-\lambda) f(x_2)$$
Geometricky: úsečka mezi dvěma body na grafu leží nad grafem.
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# Konvexní funkce
x = np.linspace(-3, 3, 100)
f_convex = x**2
ax1.plot(x, f_convex, 'b-', lw=2, label='f(x) = x²')
# Úsečka mezi dvěma body
x1, x2 = -2, 2
ax1.plot([x1, x2], [f_convex[25], f_convex[75]], 'r--', lw=2, label='Úsečka')
ax1.fill_between(x[(x >= x1) & (x <= x2)],
f_convex[(x >= x1) & (x <= x2)],
alpha=0.3, color='green', label='Graf pod úsečkou')
ax1.set_xlabel('x')
ax1.set_ylabel('f(x)')
ax1.set_title('Konvexní funkce')
ax1.legend()
ax1.grid(True, alpha=0.3)
# Nekonvexní funkce
f_nonconvex = np.sin(2*x) + 0.5*x**2
ax2.plot(x, f_nonconvex, 'b-', lw=2, label='f(x) = sin(2x) + 0.5x²')
ax2.set_xlabel('x')
ax2.set_ylabel('f(x)')
ax2.set_title('Nekonvexní funkce')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("Konvexní: x², ||x||², logistická regrese loss")
print("Nekonvexní: loss funkce neuronových sítí!")
```
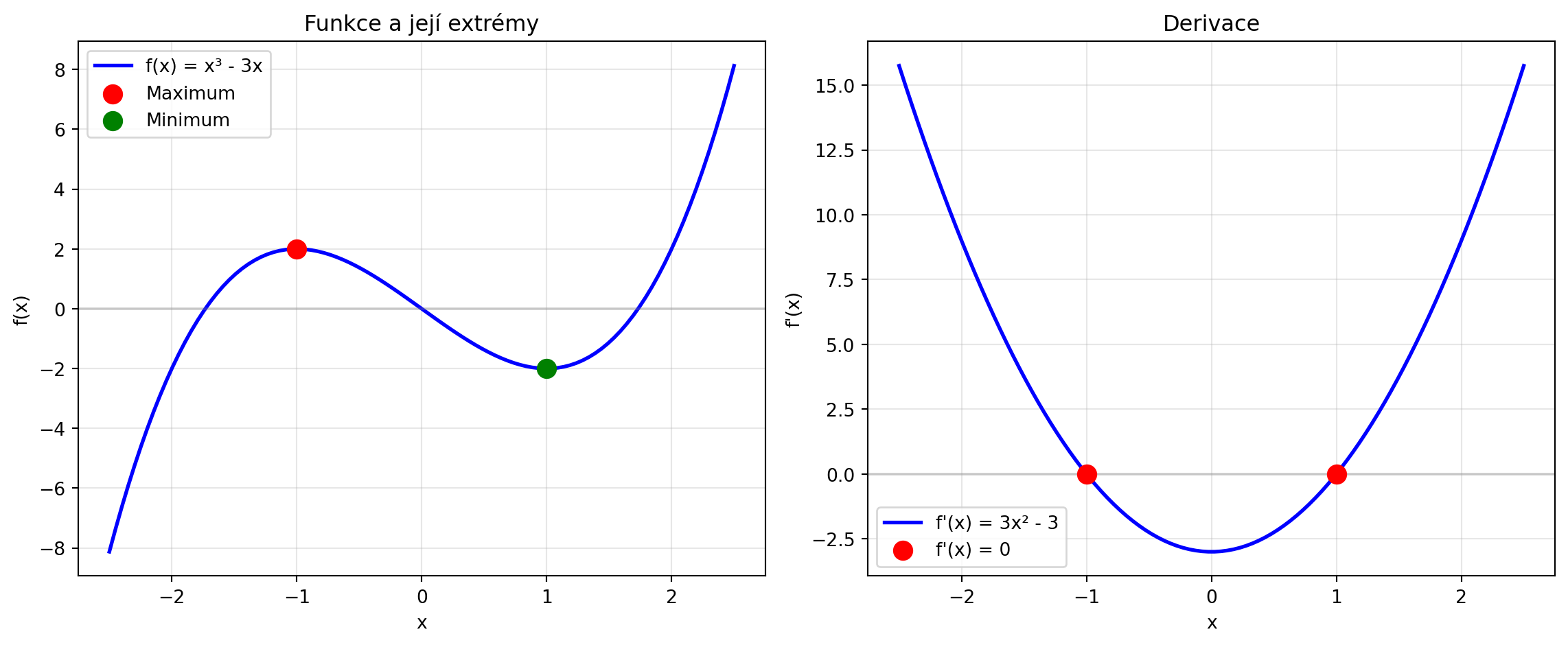
## Podmínky optima
Jak poznáme, že jsme v minimu? Derivace nám pomůže:
::: {.callout-note}
## Nutné podmínky pro minimum
**1D funkce** $f(x)$:
- Nutná podmínka: $f'(x^*) = 0$
- Postačující: $f''(x^*) > 0$
**Více proměnných** $f(\mathbf{x})$:
- Nutná podmínka: $\nabla f(\mathbf{x}^*) = \mathbf{0}$ (gradient je nulový)
- Postačující: Hessova matice je pozitivně definitní
:::
```{python}
# Příklad: f(x) = x³ - 3x
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**3 - 3*x
def f_deriv(x):
return 3*x**2 - 3
def f_deriv2(x):
return 6*x
x = np.linspace(-2.5, 2.5, 100)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# Funkce
ax1.plot(x, f(x), 'b-', lw=2, label='f(x) = x³ - 3x')
ax1.axhline(y=0, color='gray', linestyle='-', alpha=0.3)
# Stacionární body kde f'(x) = 0
stat_points = [-1, 1]
for sp in stat_points:
color = 'green' if f_deriv2(sp) > 0 else 'red'
label = 'Minimum' if f_deriv2(sp) > 0 else 'Maximum'
ax1.scatter([sp], [f(sp)], color=color, s=100, zorder=5, label=label)
ax1.set_xlabel('x')
ax1.set_ylabel('f(x)')
ax1.set_title('Funkce a její extrémy')
ax1.legend()
ax1.grid(True, alpha=0.3)
# Derivace
ax2.plot(x, f_deriv(x), 'b-', lw=2, label="f'(x) = 3x² - 3")
ax2.axhline(y=0, color='gray', linestyle='-', alpha=0.3)
ax2.scatter(stat_points, [0, 0], color='red', s=100, zorder=5, label="f'(x) = 0")
ax2.set_xlabel('x')
ax2.set_ylabel("f'(x)")
ax2.set_title('Derivace')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("Stacionární body (f'(x) = 0):")
for sp in stat_points:
typ = "minimum" if f_deriv2(sp) > 0 else "maximum"
print(f" x = {sp}: f''({sp}) = {f_deriv2(sp)} → {typ}")
```
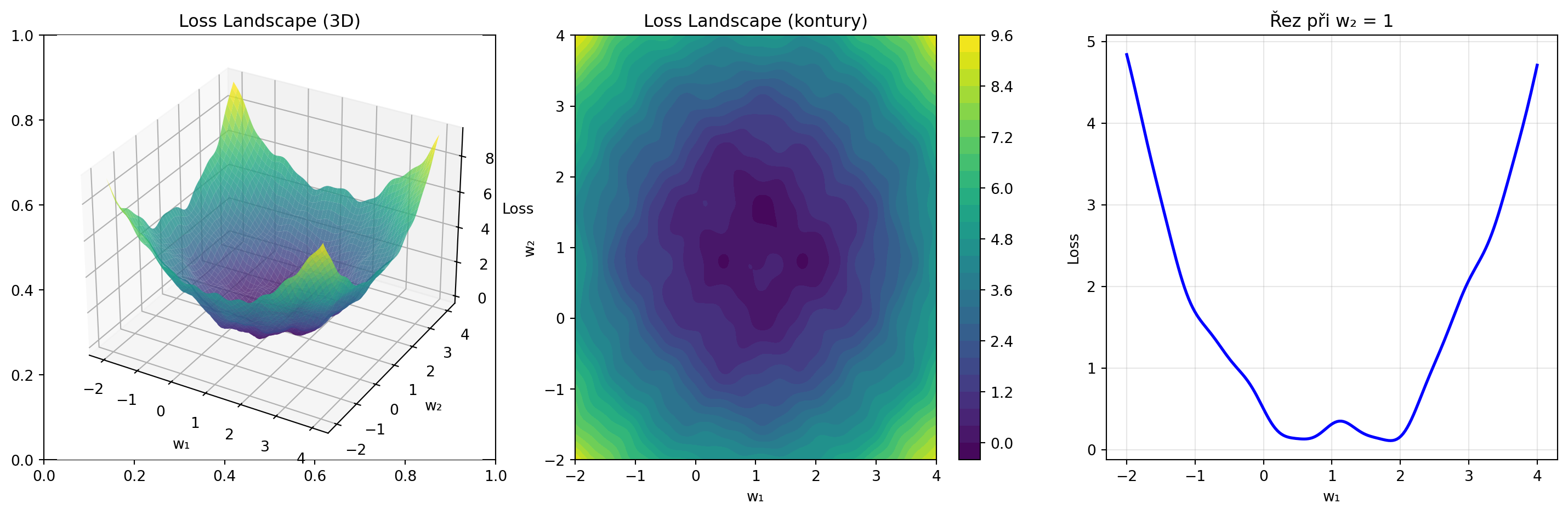
## Loss landscape neuronových sítí
Loss landscape skutečných neuronových sítí je velmi složitý:
```{python}
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
def realistic_loss(x, y):
"""Simulace realistického loss landscape."""
# Hlavní "údolí"
base = 0.5 * ((x - 1)**2 + (y - 1)**2)
# Lokální minima
local = 0.3 * np.sin(4*x) * np.cos(4*y)
# Sedlové body
saddle = 0.2 * np.sin(2*x) * np.sin(2*y)
# Náhodný šum
noise = 0.1 * np.sin(10*x) * np.cos(8*y)
return base + local + saddle + noise
x = np.linspace(-2, 4, 200)
y = np.linspace(-2, 4, 200)
X, Y = np.meshgrid(x, y)
Z = realistic_loss(X, Y)
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# 3D pohled
ax1 = fig.add_subplot(131, projection='3d')
ax1.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
ax1.set_xlabel('w₁')
ax1.set_ylabel('w₂')
ax1.set_zlabel('Loss')
ax1.set_title('Loss Landscape (3D)')
# Kontury
ax2 = axes[1]
contour = ax2.contourf(X, Y, Z, levels=30, cmap='viridis')
plt.colorbar(contour, ax=ax2)
ax2.set_xlabel('w₁')
ax2.set_ylabel('w₂')
ax2.set_title('Loss Landscape (kontury)')
# Řez
ax3 = axes[2]
mid_y = len(y) // 2
ax3.plot(x, Z[mid_y, :], 'b-', lw=2)
ax3.set_xlabel('w₁')
ax3.set_ylabel('Loss')
ax3.set_title('Řez při w₂ = 1')
ax3.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
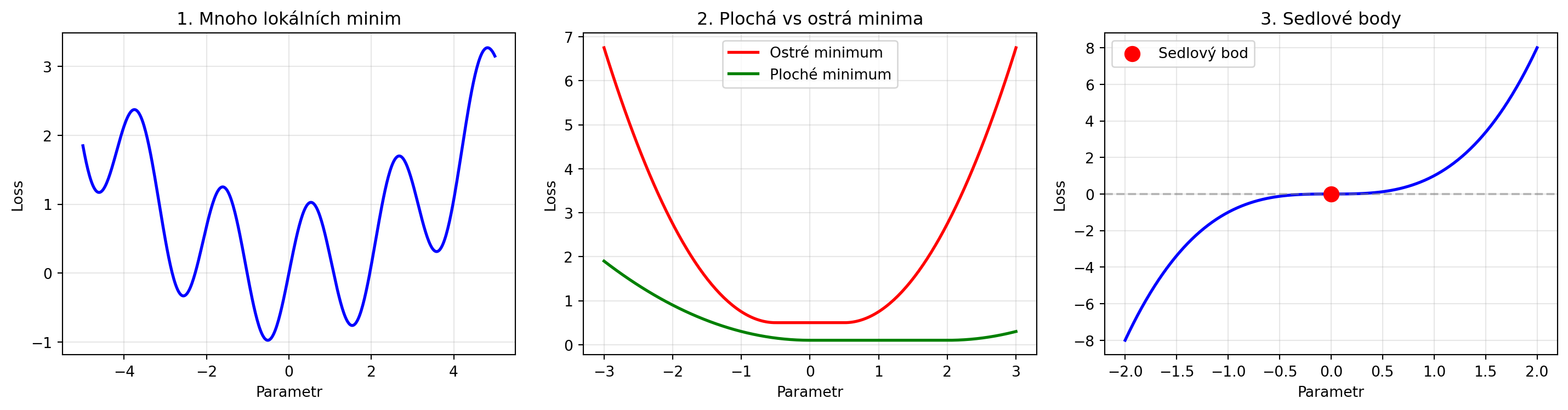
### Vlastnosti loss landscape v deep learning
```{python}
import numpy as np
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# 1. Mnoho lokálních minim
ax1 = axes[0]
x = np.linspace(-5, 5, 500)
y1 = np.sin(3*x) + 0.1*x**2
ax1.plot(x, y1, 'b-', lw=2)
ax1.set_title('1. Mnoho lokálních minim')
ax1.set_xlabel('Parametr')
ax1.set_ylabel('Loss')
ax1.grid(True, alpha=0.3)
# 2. Plochá minima vs ostrá minima
ax2 = axes[1]
x = np.linspace(-3, 3, 200)
# Ostré minimum
sharp = np.where(np.abs(x) < 0.5, 0, (np.abs(x) - 0.5)**2)
# Ploché minimum
flat = np.where(np.abs(x - 1) < 1, 0.1, 0.1 + (np.abs(x - 1) - 1)**2 * 0.2)
ax2.plot(x, sharp + 0.5, 'r-', lw=2, label='Ostré minimum')
ax2.plot(x, flat, 'g-', lw=2, label='Ploché minimum')
ax2.set_title('2. Plochá vs ostrá minima')
ax2.set_xlabel('Parametr')
ax2.set_ylabel('Loss')
ax2.legend()
ax2.grid(True, alpha=0.3)
# 3. Sedlové body
ax3 = axes[2]
x = np.linspace(-2, 2, 100)
y = x**3
ax3.plot(x, y, 'b-', lw=2)
ax3.scatter([0], [0], color='red', s=100, zorder=5, label='Sedlový bod')
ax3.axhline(y=0, color='gray', linestyle='--', alpha=0.5)
ax3.set_title('3. Sedlové body')
ax3.set_xlabel('Parametr')
ax3.set_ylabel('Loss')
ax3.legend()
ax3.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("Zajímavý fakt: Plochá minima často generalizují lépe!")
print("Ostrá minima mohou vést k přetrénování.")
```
## Metody optimalizace
Existuje mnoho metod pro hledání minima:
### 1. Analytické řešení (vzácné)
Pro jednoduché případy můžeme minimum najít analyticky:
```{python}
import sympy as sp
x = sp.Symbol('x')
f = (x - 3)**2 + 2*x + 5
# Derivace
f_prime = sp.diff(f, x)
print(f"f(x) = {f}")
print(f"f'(x) = {f_prime}")
# Řešení f'(x) = 0
kriticke_body = sp.solve(f_prime, x)
print(f"Kritické body: {kriticke_body}")
# Druhá derivace pro ověření
f_double_prime = sp.diff(f_prime, x)
print(f"f''(x) = {f_double_prime} > 0 → minimum")
```
### 2. Grid Search (hrubá síla)
Vyhodnotíme funkci na mřížce bodů:
```{python}
import numpy as np
def f_2d(x, y):
return (x - 1)**2 + (y + 0.5)**2
# Grid search
x_grid = np.linspace(-3, 5, 50)
y_grid = np.linspace(-4, 3, 50)
best_x, best_y = None, None
best_loss = float('inf')
for x in x_grid:
for y in y_grid:
loss = f_2d(x, y)
if loss < best_loss:
best_loss = loss
best_x, best_y = x, y
print(f"Grid Search výsledek:")
print(f" Nejlepší bod: ({best_x:.3f}, {best_y:.3f})")
print(f" Loss: {best_loss:.6f}")
print(f"\nSkutečné minimum: (1.0, -0.5) s loss = 0")
```
### 3. Náhodné hledání
```{python}
import numpy as np
np.random.seed(42)
n_samples = 1000
x_random = np.random.uniform(-3, 5, n_samples)
y_random = np.random.uniform(-4, 3, n_samples)
losses = [f_2d(x, y) for x, y in zip(x_random, y_random)]
best_idx = np.argmin(losses)
print(f"Náhodné hledání ({n_samples} vzorků):")
print(f" Nejlepší bod: ({x_random[best_idx]:.3f}, {y_random[best_idx]:.3f})")
print(f" Loss: {losses[best_idx]:.6f}")
```
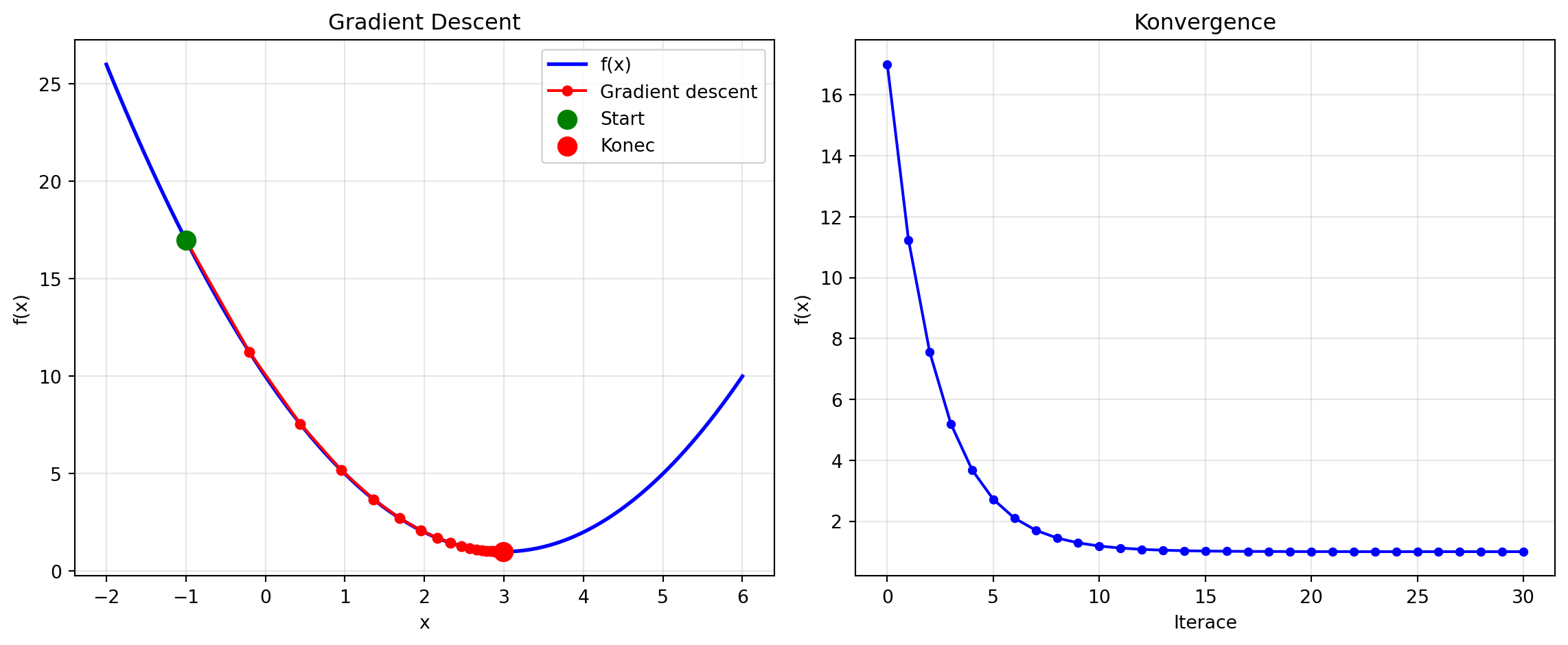
### 4. Gradient Descent (nejdůležitější!)
Klíčová metoda pro strojové učení - využívá gradient k "sestupu" do minima:
```{python}
import numpy as np
import matplotlib.pyplot as plt
def gradient_descent_demo(f, grad_f, x0, learning_rate=0.1, n_steps=50):
"""Demonstrace gradient descent."""
path = [x0]
x = x0
for _ in range(n_steps):
grad = grad_f(x)
x = x - learning_rate * grad
path.append(x)
return np.array(path)
# Funkce a její gradient
def f(x):
return (x - 3)**2 + 1
def grad_f(x):
return 2 * (x - 3)
# Gradient descent
x0 = -1
path = gradient_descent_demo(f, grad_f, x0, learning_rate=0.1, n_steps=30)
# Vizualizace
x = np.linspace(-2, 6, 100)
plt.figure(figsize=(12, 5))
# Funkce a cesta
plt.subplot(1, 2, 1)
plt.plot(x, f(x), 'b-', lw=2, label='f(x)')
plt.plot(path, f(path), 'ro-', markersize=5, label='Gradient descent')
plt.scatter([path[0]], [f(path[0])], color='green', s=100, zorder=5, label='Start')
plt.scatter([path[-1]], [f(path[-1])], color='red', s=100, zorder=5, label='Konec')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Gradient Descent')
plt.legend()
plt.grid(True, alpha=0.3)
# Konvergence
plt.subplot(1, 2, 2)
plt.plot(f(path), 'b.-', markersize=8)
plt.xlabel('Iterace')
plt.ylabel('f(x)')
plt.title('Konvergence')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print(f"Start: x = {path[0]:.4f}, f(x) = {f(path[0]):.4f}")
print(f"Konec: x = {path[-1]:.4f}, f(x) = {f(path[-1]):.4f}")
print(f"Optimum: x = 3.0, f(x) = 1.0")
```
## Řešené příklady
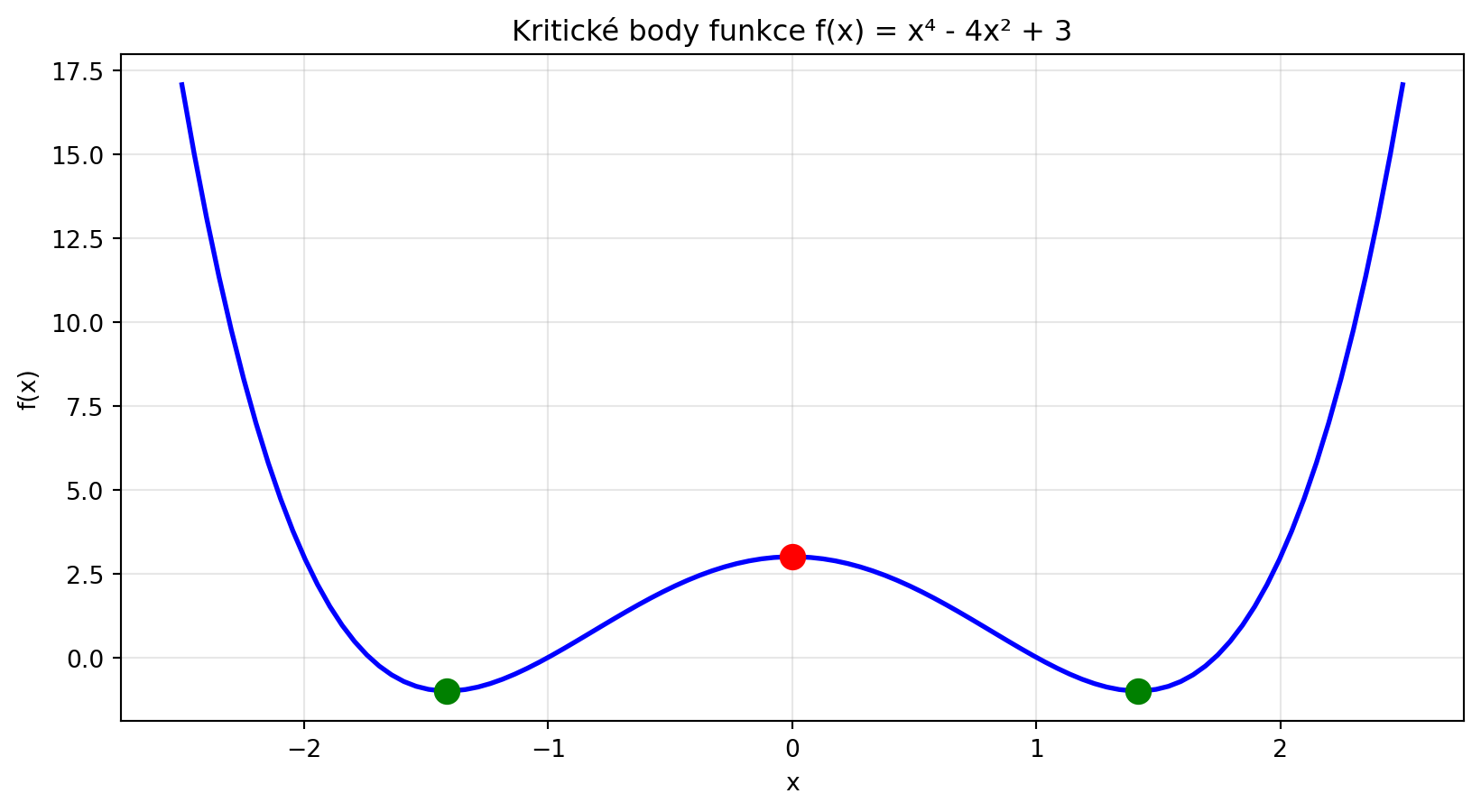
### Příklad 1: Klasifikace typu kritického bodu
**Zadání**: Pro funkci $f(x) = x^4 - 4x^2 + 3$ najděte všechny kritické body a určete jejich typ.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
x = sp.Symbol('x')
f = x**4 - 4*x**2 + 3
f_prime = sp.diff(f, x)
f_double_prime = sp.diff(f_prime, x)
print(f"f(x) = {f}")
print(f"f'(x) = {f_prime}")
print(f"f''(x) = {f_double_prime}")
kriticke_body = sp.solve(f_prime, x)
print(f"\nKritické body: {kriticke_body}")
for kb in kriticke_body:
hodnota_f = f.subs(x, kb)
hodnota_f2 = f_double_prime.subs(x, kb)
if hodnota_f2 > 0:
typ = "lokální minimum"
elif hodnota_f2 < 0:
typ = "lokální maximum"
else:
typ = "inflexní bod"
print(f" x = {kb}: f''({kb}) = {hodnota_f2} → {typ}, f({kb}) = {hodnota_f}")
# Vizualizace
x_num = np.linspace(-2.5, 2.5, 100)
f_num = x_num**4 - 4*x_num**2 + 3
plt.figure(figsize=(10, 5))
plt.plot(x_num, f_num, 'b-', lw=2)
for kb in kriticke_body:
kb_float = float(kb)
f_val = float(f.subs(x, kb))
f2_val = float(f_double_prime.subs(x, kb))
color = 'green' if f2_val > 0 else 'red'
plt.scatter([kb_float], [f_val], color=color, s=100, zorder=5)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Kritické body funkce f(x) = x⁴ - 4x² + 3')
plt.grid(True, alpha=0.3)
plt.show()
```
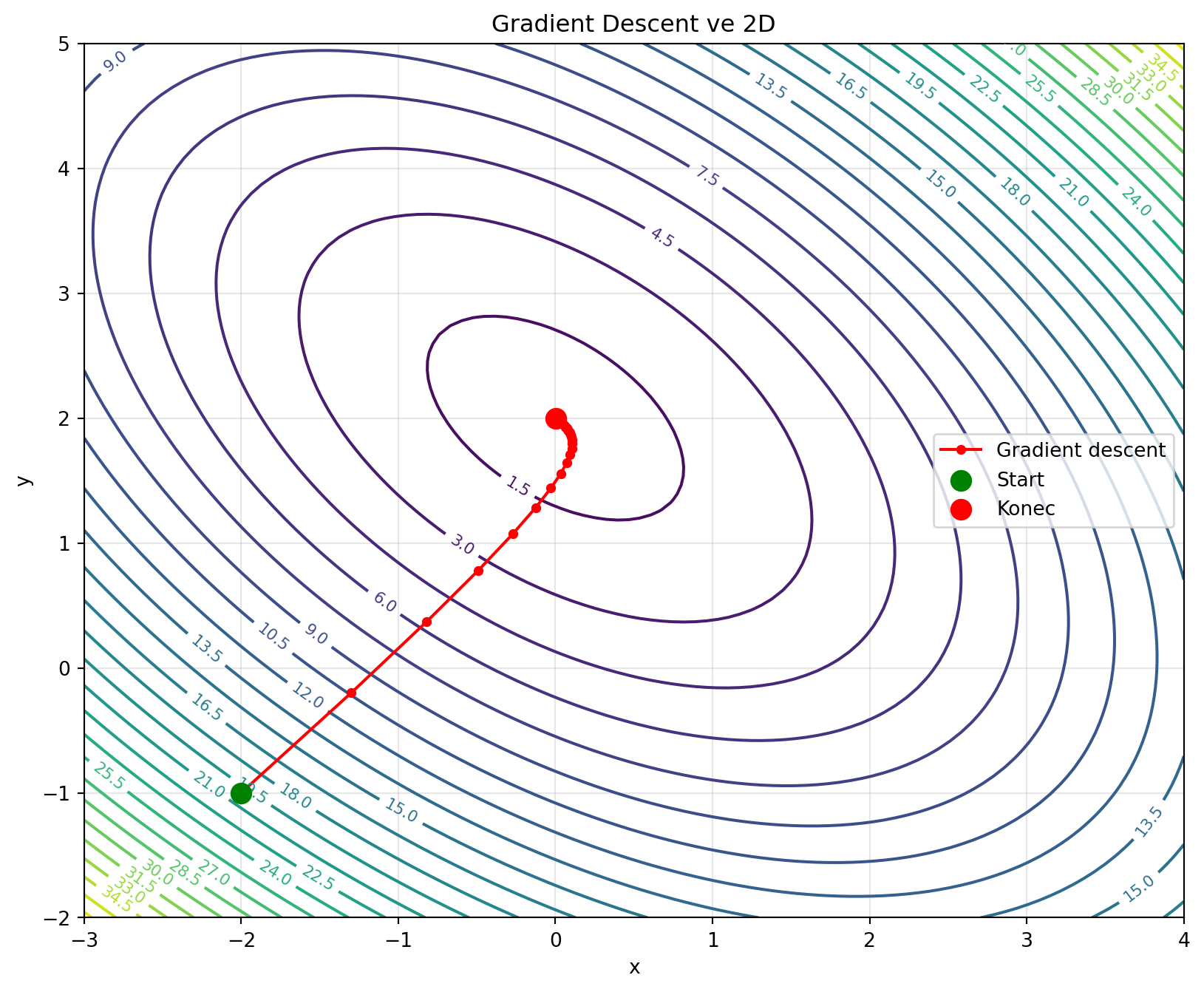
### Příklad 2: Optimalizace ve 2D
**Zadání**: Najděte minimum funkce $f(x, y) = (x-1)^2 + (y-2)^2 + xy$ pomocí gradient descent.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
def f_2d(x, y):
return (x - 1)**2 + (y - 2)**2 + x*y
def grad_f_2d(x, y):
df_dx = 2*(x - 1) + y
df_dy = 2*(y - 2) + x
return np.array([df_dx, df_dy])
# Gradient descent
pos = np.array([-2.0, -1.0]) # Start
learning_rate = 0.1
path = [pos.copy()]
for _ in range(50):
grad = grad_f_2d(pos[0], pos[1])
pos = pos - learning_rate * grad
path.append(pos.copy())
path = np.array(path)
# Vizualizace
x = np.linspace(-3, 4, 100)
y = np.linspace(-2, 5, 100)
X, Y = np.meshgrid(x, y)
Z = f_2d(X, Y)
plt.figure(figsize=(10, 8))
contour = plt.contour(X, Y, Z, levels=30, cmap='viridis')
plt.clabel(contour, inline=True, fontsize=8)
plt.plot(path[:, 0], path[:, 1], 'ro-', markersize=4, label='Gradient descent')
plt.scatter([path[0, 0]], [path[0, 1]], color='green', s=100, zorder=5, label='Start')
plt.scatter([path[-1, 0]], [path[-1, 1]], color='red', s=100, zorder=5, label='Konec')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Gradient Descent ve 2D')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
print(f"Start: ({path[0, 0]:.4f}, {path[0, 1]:.4f})")
print(f"Konec: ({path[-1, 0]:.4f}, {path[-1, 1]:.4f})")
print(f"Finální loss: {f_2d(path[-1, 0], path[-1, 1]):.6f}")
```
### Příklad 3: Porovnání learning rate
**Zadání**: Ukažte vliv learning rate na konvergenci gradient descent.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return (x - 2)**2
def grad_f(x):
return 2 * (x - 2)
learning_rates = [0.01, 0.1, 0.5, 0.9, 1.1]
x0 = -3
fig, axes = plt.subplots(1, len(learning_rates), figsize=(20, 4))
for ax, lr in zip(axes, learning_rates):
x = x0
path = [x]
for _ in range(30):
x = x - lr * grad_f(x)
path.append(x)
if abs(x) > 100: # Divergence
break
path = np.array(path)
x_range = np.linspace(-5, 8, 100)
ax.plot(x_range, f(x_range), 'b-', lw=2)
if len(path) > 1 and not np.any(np.isnan(path)) and np.max(np.abs(path)) < 100:
ax.plot(path, f(path), 'ro-', markersize=4)
ax.set_title(f'lr = {lr}')
ax.set_xlabel('x')
ax.set_ylabel('f(x)')
ax.set_ylim(-1, 30)
ax.grid(True, alpha=0.3)
status = "OK" if np.abs(path[-1] - 2) < 0.1 else ("Pomalé" if np.abs(path[-1] - 2) < 1 else "Diverguje!")
ax.text(0.5, 0.95, status, transform=ax.transAxes, ha='center', fontsize=12,
color='green' if status == "OK" else 'orange' if status == "Pomalé" else 'red')
plt.tight_layout()
plt.show()
```
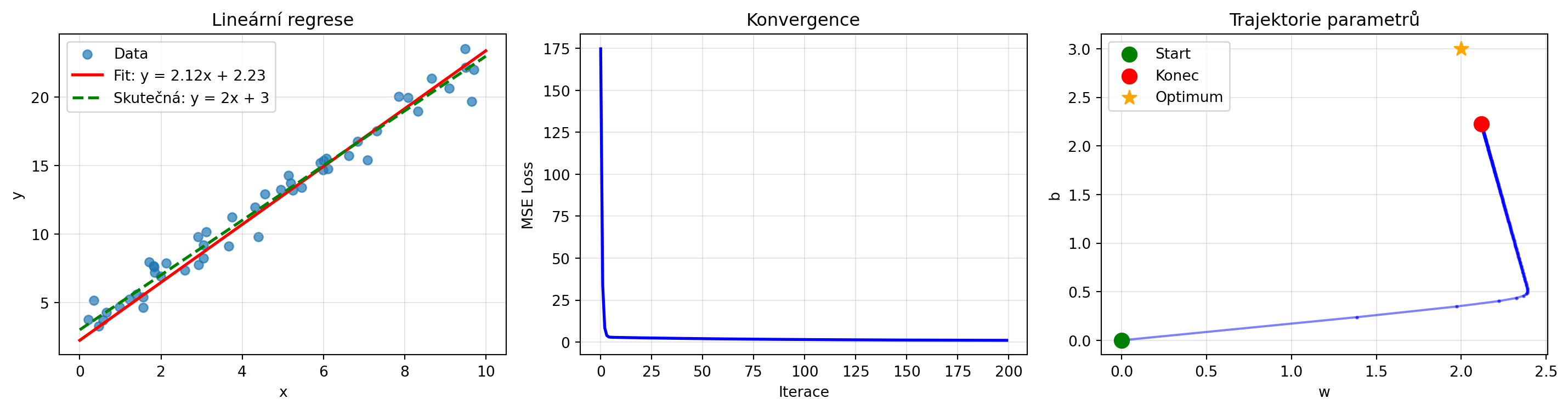
### Příklad 4: Lineární regrese jako optimalizace
**Zadání**: Formulujte lineární regresi jako optimalizační problém a řešte gradient descent.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
# Generování dat
n = 50
X = np.random.uniform(0, 10, n)
y_true = 2 * X + 3 + np.random.normal(0, 1, n)
# Loss funkce: MSE
def mse_loss(w, b, X, y):
predictions = w * X + b
return np.mean((predictions - y)**2)
# Gradient MSE
def mse_gradient(w, b, X, y):
predictions = w * X + b
errors = predictions - y
dw = 2 * np.mean(errors * X)
db = 2 * np.mean(errors)
return dw, db
# Gradient descent
w, b = 0.0, 0.0
learning_rate = 0.01
losses = []
params = [(w, b)]
for _ in range(200):
loss = mse_loss(w, b, X, y_true)
losses.append(loss)
dw, db = mse_gradient(w, b, X, y_true)
w -= learning_rate * dw
b -= learning_rate * db
params.append((w, b))
# Vizualizace
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# Data a fit
ax1 = axes[0]
ax1.scatter(X, y_true, alpha=0.7, label='Data')
x_line = np.linspace(0, 10, 100)
ax1.plot(x_line, w * x_line + b, 'r-', lw=2, label=f'Fit: y = {w:.2f}x + {b:.2f}')
ax1.plot(x_line, 2 * x_line + 3, 'g--', lw=2, label='Skutečná: y = 2x + 3')
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.set_title('Lineární regrese')
ax1.legend()
ax1.grid(True, alpha=0.3)
# Loss
ax2 = axes[1]
ax2.plot(losses, 'b-', lw=2)
ax2.set_xlabel('Iterace')
ax2.set_ylabel('MSE Loss')
ax2.set_title('Konvergence')
ax2.grid(True, alpha=0.3)
# Trajektorie parametrů
ax3 = axes[2]
params = np.array(params)
ax3.plot(params[:, 0], params[:, 1], 'b.-', markersize=3, alpha=0.5)
ax3.scatter([0], [0], color='green', s=100, zorder=5, label='Start')
ax3.scatter([w], [b], color='red', s=100, zorder=5, label='Konec')
ax3.scatter([2], [3], color='orange', s=100, marker='*', zorder=5, label='Optimum')
ax3.set_xlabel('w')
ax3.set_ylabel('b')
ax3.set_title('Trajektorie parametrů')
ax3.legend()
ax3.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print(f"Naučené parametry: w = {w:.4f}, b = {b:.4f}")
print(f"Skutečné parametry: w = 2.0, b = 3.0")
print(f"Finální MSE: {losses[-1]:.4f}")
```
## Python v praxi: Gradient Descent optimalizace
```{python}
# 1D optimalizace pomocí gradient descent
import numpy as np
def f_1d(x):
return (x - 3)**2 + np.sin(2*x)
def grad_f_1d(x):
return 2*(x - 3) + 2*np.cos(2*x)
def optimize_1d(f, grad_f, x0, lr=0.1, n_iter=100):
x = x0
for _ in range(n_iter):
x = x - lr * grad_f(x)
return x, f(x)
x_min, f_min = optimize_1d(f_1d, grad_f_1d, x0=0.0)
print("1D optimalizace (gradient descent):")
print(f" Minimum při x = {x_min:.4f}")
print(f" f(x) = {f_min:.4f}")
# 2D optimalizace
def f_2d(params):
x, y = params
return (x - 1)**2 + (y - 2)**2 + 0.5*x*y
def grad_f_2d(params):
x, y = params
dx = 2*(x - 1) + 0.5*y
dy = 2*(y - 2) + 0.5*x
return np.array([dx, dy])
def optimize_2d(f, grad_f, x0, lr=0.1, n_iter=100):
x = np.array(x0, dtype=float)
for i in range(n_iter):
x = x - lr * grad_f(x)
return x, f(x), i+1
x_min, f_min, n_iter = optimize_2d(f_2d, grad_f_2d, x0=[0.0, 0.0])
print(f"\n2D optimalizace (gradient descent):")
print(f" Minimum při (x, y) = ({x_min[0]:.4f}, {x_min[1]:.4f})")
print(f" f(x, y) = {f_min:.4f}")
print(f" Počet iterací: {n_iter}")
```
## Cvičení
::: {.callout-note icon=false}
## Cvičení 1: Kritické body
Najděte všechny kritické body funkce $f(x) = x^3 - 6x^2 + 9x + 1$ a určete, které jsou lokální minima, maxima nebo inflexní body.
:::
::: {.callout-note icon=false}
## Cvičení 2: Konvexnost
Dokažte, že funkce $f(x) = e^x$ je konvexní. Hint: Spočítejte druhou derivaci.
:::
::: {.callout-note icon=false}
## Cvičení 3: Grid search vs random search
Porovnejte grid search a random search pro funkci $f(x, y) = (x-\pi)^2 + (y-e)^2$ na oblasti $[0, 5] \times [0, 5]$. Kolik evaluací potřebuje každá metoda k nalezení minima s přesností 0.1?
:::
::: {.callout-note icon=false}
## Cvičení 4: Sedlové body
Pro funkci $f(x, y) = x^2 - y^2 + 2xy$ najděte všechny stacionární body a klasifikujte je pomocí Hessovy matice.
:::
::: {.callout-note icon=false}
## Cvičení 5: Polynomiální regrese
Rozšiřte příklad lineární regrese na polynomiální regresi stupně 2: $y = w_2 x^2 + w_1 x + w_0$. Implementujte gradient descent pro nalezení optimálních koeficientů.
:::
## Shrnutí
::: {.callout-tip}
## Co jsme se naučili
1. **Optimalizace** je hledání parametrů minimalizujících loss funkci
2. **Lokální minimum** ≠ **globální minimum** - ale v deep learning to často nevadí
3. **Konvexní funkce** mají jediné globální minimum
4. **Sedlové body** jsou místa s nulovým gradientem, která nejsou extrémy
5. **Nutná podmínka** pro minimum: $\nabla f = 0$
6. **Gradient descent** je klíčová metoda - následuje záporný gradient
7. **Learning rate** určuje velikost kroků a ovlivňuje konvergenci
:::
::: {.callout-important}
## Klíčové pojmy
- **Loss funkce**: Měří kvalitu modelu
- **Globální/lokální minimum**: Nejnižší bod celkově/v okolí
- **Sedlový bod**: Stacionární bod, který není extrém
- **Konvexní funkce**: Každé lokální minimum je globální
- **Gradient descent**: Iterativní metoda sledující záporný gradient
- **Learning rate**: Velikost kroku v gradient descent
:::
V další kapitole se podrobně podíváme na gradient descent - nejdůležitější optimalizační algoritmus v strojovém učení.