# Vícevrstvé sítě {#sec-mlp}
## Motivace: Překonání limitů perceptronu
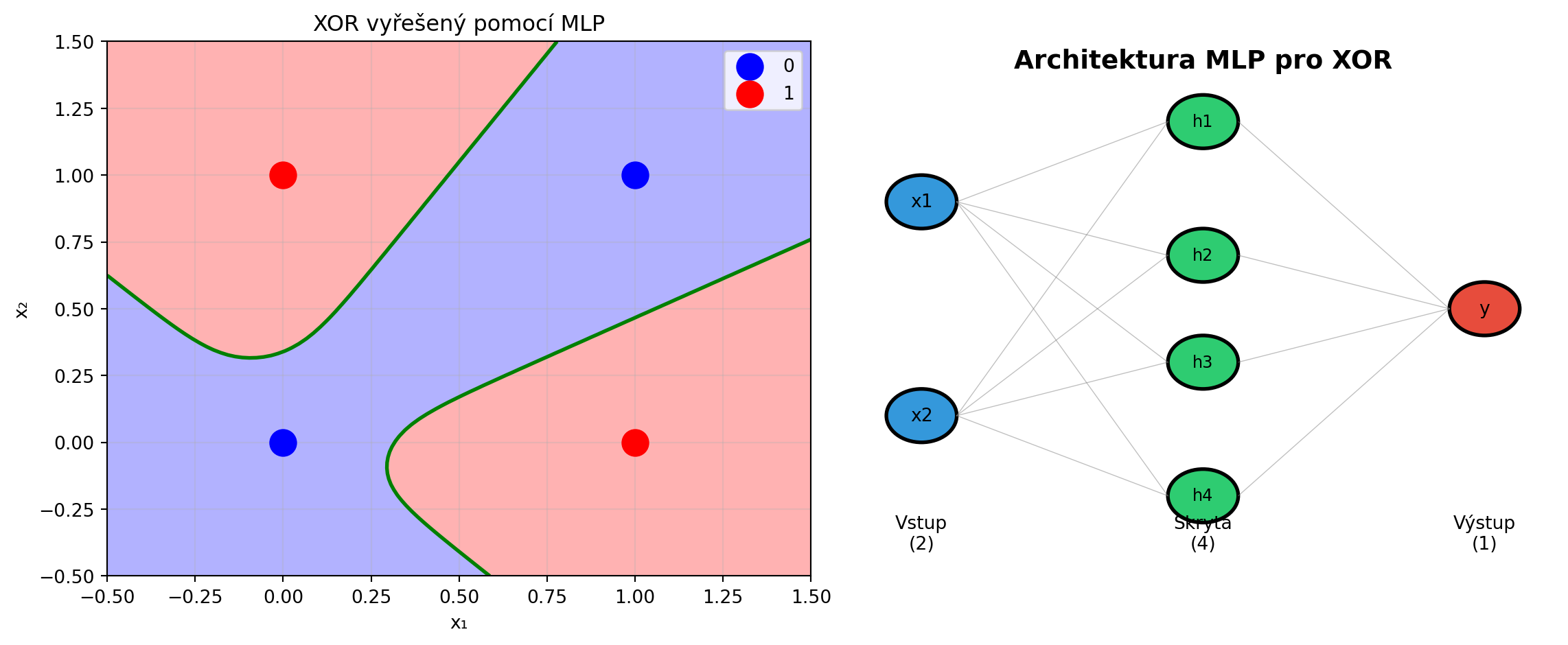
V minulé kapitole jsme viděli, že jeden perceptron nezvládne problém XOR - nedokáže klasifikovat data, která nejsou lineárně separabilní. Řešením je **skládat více vrstev** neuronů.
**Vícevrstvý perceptron** (Multi-Layer Perceptron, MLP) dokáže aproximovat libovolnou spojitou funkci - je to **univerzální aproximátor**.
```{python}
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
# XOR problém - řešený MLP
X_xor = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y_xor = np.array([0, 1, 1, 0])
# Vizualizace nelineární rozhodovací hranice
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# XOR data
ax1.scatter(X_xor[y_xor==0, 0], X_xor[y_xor==0, 1], c='blue', s=200, label='0', zorder=5)
ax1.scatter(X_xor[y_xor==1, 0], X_xor[y_xor==1, 1], c='red', s=200, label='1', zorder=5)
# Natrénovaná MLP rozhodovací hranice
torch.manual_seed(42)
model = nn.Sequential(
nn.Linear(2, 4),
nn.Tanh(),
nn.Linear(4, 1),
nn.Sigmoid()
)
X_tensor = torch.FloatTensor(X_xor)
y_tensor = torch.FloatTensor(y_xor).unsqueeze(1)
optimizer = torch.optim.Adam(model.parameters(), lr=0.1)
criterion = nn.BCELoss()
for _ in range(1000):
optimizer.zero_grad()
loss = criterion(model(X_tensor), y_tensor)
loss.backward()
optimizer.step()
# Rozhodovací hranice
xx, yy = np.meshgrid(np.linspace(-0.5, 1.5, 100), np.linspace(-0.5, 1.5, 100))
grid = torch.FloatTensor(np.c_[xx.ravel(), yy.ravel()])
with torch.no_grad():
Z = model(grid).numpy().reshape(xx.shape)
ax1.contourf(xx, yy, Z, levels=[0, 0.5, 1], colors=['blue', 'red'], alpha=0.3)
ax1.contour(xx, yy, Z, levels=[0.5], colors='green', linewidths=2)
ax1.set_xlabel('x₁')
ax1.set_ylabel('x₂')
ax1.set_title('XOR vyřešený pomocí MLP')
ax1.legend()
ax1.grid(True, alpha=0.3)
# Architektura sítě
ax2.text(0.5, 0.95, 'Architektura MLP pro XOR', ha='center', fontsize=14, fontweight='bold', transform=ax2.transAxes)
# Vstupní vrstva
for i, y in enumerate([0.7, 0.3]):
circle = plt.Circle((0.1, y), 0.05, color='#3498db', ec='black', lw=2)
ax2.add_patch(circle)
ax2.text(0.1, y, f'x{i+1}', ha='center', va='center', fontsize=10)
# Skrytá vrstva
for i, y in enumerate([0.85, 0.6, 0.4, 0.15]):
circle = plt.Circle((0.5, y), 0.05, color='#2ecc71', ec='black', lw=2)
ax2.add_patch(circle)
ax2.text(0.5, y, f'h{i+1}', ha='center', va='center', fontsize=9)
# Výstupní vrstva
circle = plt.Circle((0.9, 0.5), 0.05, color='#e74c3c', ec='black', lw=2)
ax2.add_patch(circle)
ax2.text(0.9, 0.5, 'y', ha='center', va='center', fontsize=10)
# Spojení
for y_in in [0.7, 0.3]:
for y_h in [0.85, 0.6, 0.4, 0.15]:
ax2.plot([0.15, 0.45], [y_in, y_h], 'gray', lw=0.5, alpha=0.5)
for y_h in [0.85, 0.6, 0.4, 0.15]:
ax2.plot([0.55, 0.85], [y_h, 0.5], 'gray', lw=0.5, alpha=0.5)
ax2.set_xlim(0, 1)
ax2.set_ylim(0, 1)
ax2.axis('off')
# Popisky vrstev
ax2.text(0.1, 0.05, 'Vstup\n(2)', ha='center', fontsize=10)
ax2.text(0.5, 0.05, 'Skrytá\n(4)', ha='center', fontsize=10)
ax2.text(0.9, 0.05, 'Výstup\n(1)', ha='center', fontsize=10)
plt.tight_layout()
plt.show()
print("MLP dokáže vytvořit nelineární rozhodovací hranici!")
```
## Architektura MLP
::: {.callout-note}
## Struktura vícevrstvé sítě
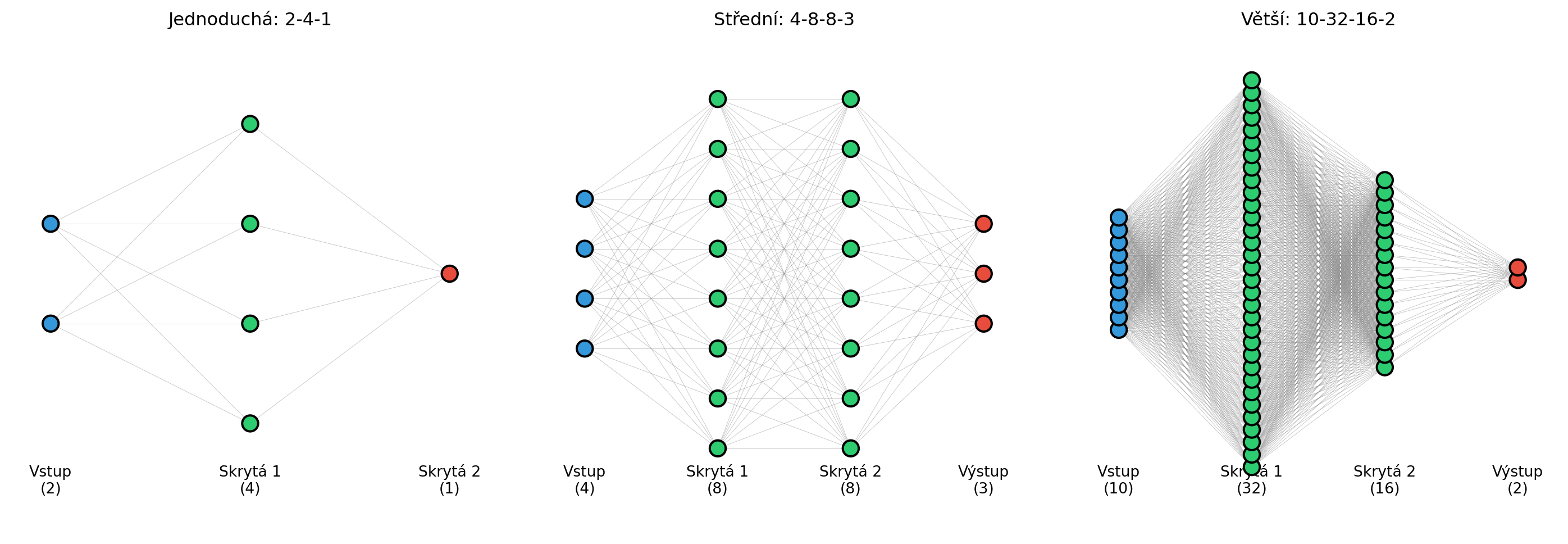
MLP se skládá z:
1. **Vstupní vrstva**: Přijímá data (není to "vrstva" v pravém slova smyslu)
2. **Skryté vrstvy**: Jedna nebo více vrstev neuronů
3. **Výstupní vrstva**: Produkuje finální predikci
Každý neuron v jedné vrstvě je propojen se všemi neurony v následující vrstvě - proto **"fully connected"** nebo **"dense"** vrstvy.
:::
```{python}
import matplotlib.pyplot as plt
def visualize_mlp(layer_sizes, ax=None):
"""Vizualizace architektury MLP."""
if ax is None:
fig, ax = plt.subplots(figsize=(12, 8))
n_layers = len(layer_sizes)
max_neurons = max(layer_sizes)
# Pozice neuronů
positions = []
for l, n_neurons in enumerate(layer_sizes):
x = l / (n_layers - 1)
y_offset = (max_neurons - n_neurons) / 2 / max_neurons
layer_pos = []
for n in range(n_neurons):
y = (n + 0.5) / max_neurons + y_offset
layer_pos.append((x, y))
positions.append(layer_pos)
# Spojení mezi vrstvami
for l in range(n_layers - 1):
for pos1 in positions[l]:
for pos2 in positions[l + 1]:
ax.plot([pos1[0], pos2[0]], [pos1[1], pos2[1]],
'gray', lw=0.3, alpha=0.5)
# Neurony
colors = ['#3498db', '#2ecc71', '#2ecc71', '#e74c3c']
layer_names = ['Vstup', 'Skrytá 1', 'Skrytá 2', 'Výstup']
for l, (layer_pos, n_neurons) in enumerate(zip(positions, layer_sizes)):
color = colors[min(l, len(colors)-1)]
if l == n_layers - 1:
color = '#e74c3c'
for pos in layer_pos:
circle = plt.Circle(pos, 0.02, color=color, ec='black', lw=1.5, zorder=5)
ax.add_patch(circle)
# Popisek
ax.text(l / (n_layers - 1), -0.05, f'{layer_names[min(l, len(layer_names)-1)]}\n({n_neurons})',
ha='center', fontsize=10)
ax.set_xlim(-0.1, 1.1)
ax.set_ylim(-0.15, 1.1)
ax.set_aspect('equal')
ax.axis('off')
return ax
# Příklady architektur
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
architectures = [
[2, 4, 1], # Jednoduchá
[4, 8, 8, 3], # Střední
[10, 32, 16, 2] # Větší
]
titles = ['Jednoduchá: 2-4-1', 'Střední: 4-8-8-3', 'Větší: 10-32-16-2']
for ax, arch, title in zip(axes, architectures, titles):
visualize_mlp(arch, ax)
ax.set_title(title, fontsize=12)
plt.tight_layout()
plt.show()
```
## Matematický popis
Pro MLP s $L$ vrstvami označíme:
- $\mathbf{a}^{(0)} = \mathbf{x}$ je vstup
- $\mathbf{W}^{(l)}$ je matice vah vrstvy $l$
- $\mathbf{b}^{(l)}$ je vektor biasů vrstvy $l$
- $\sigma^{(l)}$ je aktivační funkce vrstvy $l$
::: {.callout-note}
## Forward Pass
Pro každou vrstvu $l = 1, \ldots, L$:
$$\mathbf{z}^{(l)} = \mathbf{W}^{(l)} \mathbf{a}^{(l-1)} + \mathbf{b}^{(l)}$$
$$\mathbf{a}^{(l)} = \sigma^{(l)}(\mathbf{z}^{(l)})$$
Výstup sítě: $\hat{\mathbf{y}} = \mathbf{a}^{(L)}$
:::
```{python}
import numpy as np
def forward_pass(X, weights, biases, activations):
"""
Ruční implementace forward pass.
Args:
X: Vstupní data (batch_size, input_dim)
weights: Seznam matic vah pro každou vrstvu
biases: Seznam vektorů biasů
activations: Seznam aktivačních funkcí
"""
a = X
layer_outputs = [a]
for W, b, activation in zip(weights, biases, activations):
z = a @ W.T + b
if activation == 'relu':
a = np.maximum(0, z)
elif activation == 'sigmoid':
a = 1 / (1 + np.exp(-z))
elif activation == 'tanh':
a = np.tanh(z)
elif activation == 'softmax':
exp_z = np.exp(z - np.max(z, axis=1, keepdims=True))
a = exp_z / np.sum(exp_z, axis=1, keepdims=True)
layer_outputs.append(a)
return a, layer_outputs
# Příklad: MLP 2 -> 3 -> 1
np.random.seed(42)
# Váhy a biasy
W1 = np.random.randn(3, 2) * 0.5
b1 = np.zeros(3)
W2 = np.random.randn(1, 3) * 0.5
b2 = np.zeros(1)
# Vstup
X = np.array([[1.0, 0.5]])
# Forward pass
output, layers = forward_pass(X, [W1, W2], [b1, b2], ['relu', 'sigmoid'])
print("Forward Pass příklad:")
print(f"Vstup: {X}")
print(f"\nVrstva 1 (ReLU):")
print(f" z1 = X @ W1.T + b1 = {(X @ W1.T + b1)}")
print(f" a1 = ReLU(z1) = {layers[1]}")
print(f"\nVrstva 2 (Sigmoid):")
print(f" z2 = a1 @ W2.T + b2 = {(layers[1] @ W2.T + b2)}")
print(f" a2 = Sigmoid(z2) = {layers[2]}")
print(f"\nVýstup: {output[0, 0]:.4f}")
```
## Reprezentace jako maticové násobení
Celou síť můžeme efektivně implementovat pomocí maticových operací:
```{python}
# Batch processing - více vstupů najednou
import numpy as np
batch_size = 4
X_batch = np.random.randn(batch_size, 2)
print("Batch processing:")
print(f"Vstup: {X_batch.shape} = (batch_size, input_dim)")
# Vrstva 1
z1 = X_batch @ W1.T + b1 # (4, 2) @ (2, 3).T = (4, 3)
a1 = np.maximum(0, z1)
print(f"Po vrstvě 1: {a1.shape}")
# Vrstva 2
z2 = a1 @ W2.T + b2 # (4, 3) @ (3, 1).T = (4, 1)
a2 = 1 / (1 + np.exp(-z2))
print(f"Po vrstvě 2: {a2.shape}")
print(f"\nVšechny 4 vzorky zpracovány najednou!")
```
## MLP v PyTorch
```{python}
import torch
import torch.nn as nn
# Definice MLP
class MLP(nn.Module):
def __init__(self, input_size, hidden_sizes, output_size):
super().__init__()
layers = []
prev_size = input_size
for hidden_size in hidden_sizes:
layers.append(nn.Linear(prev_size, hidden_size))
layers.append(nn.ReLU())
prev_size = hidden_size
layers.append(nn.Linear(prev_size, output_size))
self.network = nn.Sequential(*layers)
def forward(self, x):
return self.network(x)
# Vytvoření sítě
model = MLP(input_size=2, hidden_sizes=[8, 4], output_size=1)
print("Architektura MLP v PyTorch:")
print(model)
# Počet parametrů
total_params = sum(p.numel() for p in model.parameters())
print(f"\nCelkem parametrů: {total_params}")
# Forward pass
x = torch.randn(5, 2)
output = model(x)
print(f"\nVstup: {x.shape}")
print(f"Výstup: {output.shape}")
```
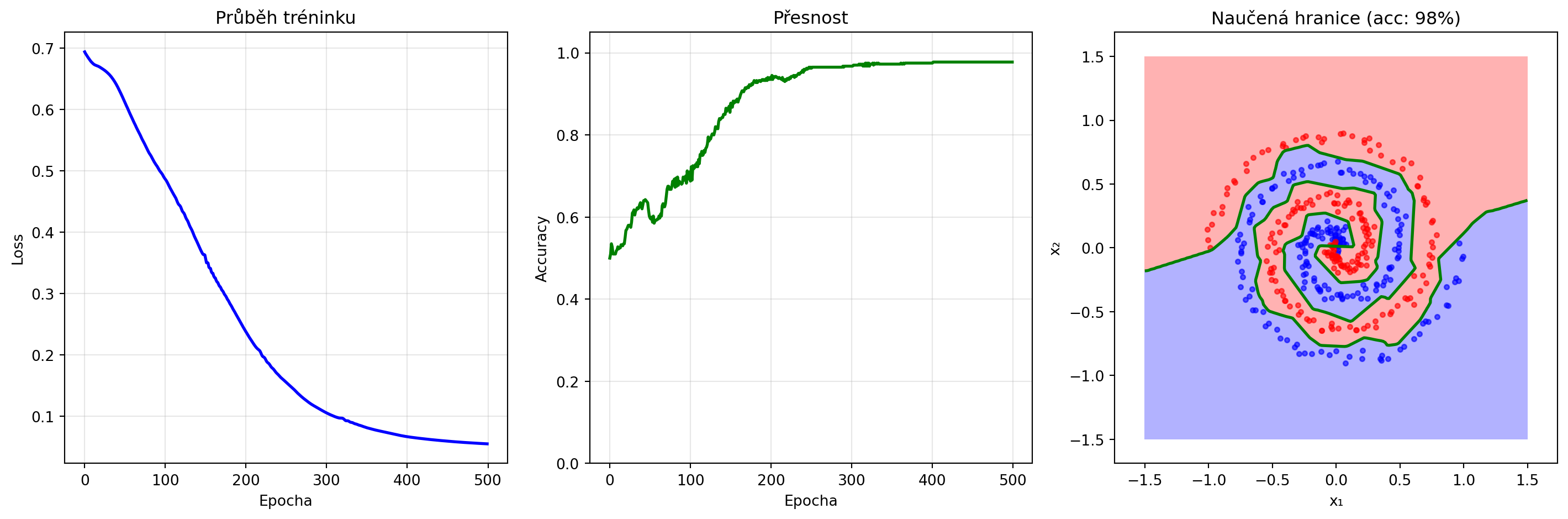
## Trénování MLP na nelineárních datech
```{python}
# Generování nelineárních dat (spirály)
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
def generate_spirals(n_points, noise=0.5):
n = n_points // 2
# Spirála 1
theta1 = np.linspace(0, 4*np.pi, n)
r1 = theta1 / (4*np.pi)
x1 = r1 * np.cos(theta1) + np.random.randn(n) * noise * 0.1
y1 = r1 * np.sin(theta1) + np.random.randn(n) * noise * 0.1
# Spirála 2 (otočená o 180°)
theta2 = np.linspace(0, 4*np.pi, n)
r2 = theta2 / (4*np.pi)
x2 = -r2 * np.cos(theta2) + np.random.randn(n) * noise * 0.1
y2 = -r2 * np.sin(theta2) + np.random.randn(n) * noise * 0.1
X = np.vstack([np.column_stack([x1, y1]), np.column_stack([x2, y2])])
y = np.array([0]*n + [1]*n)
return X, y
X_spiral, y_spiral = generate_spirals(400, noise=0.3)
# Vizualizace
plt.figure(figsize=(8, 8))
plt.scatter(X_spiral[y_spiral==0, 0], X_spiral[y_spiral==0, 1], c='blue', alpha=0.6, label='Třída 0')
plt.scatter(X_spiral[y_spiral==1, 0], X_spiral[y_spiral==1, 1], c='red', alpha=0.6, label='Třída 1')
plt.xlabel('x₁')
plt.ylabel('x₂')
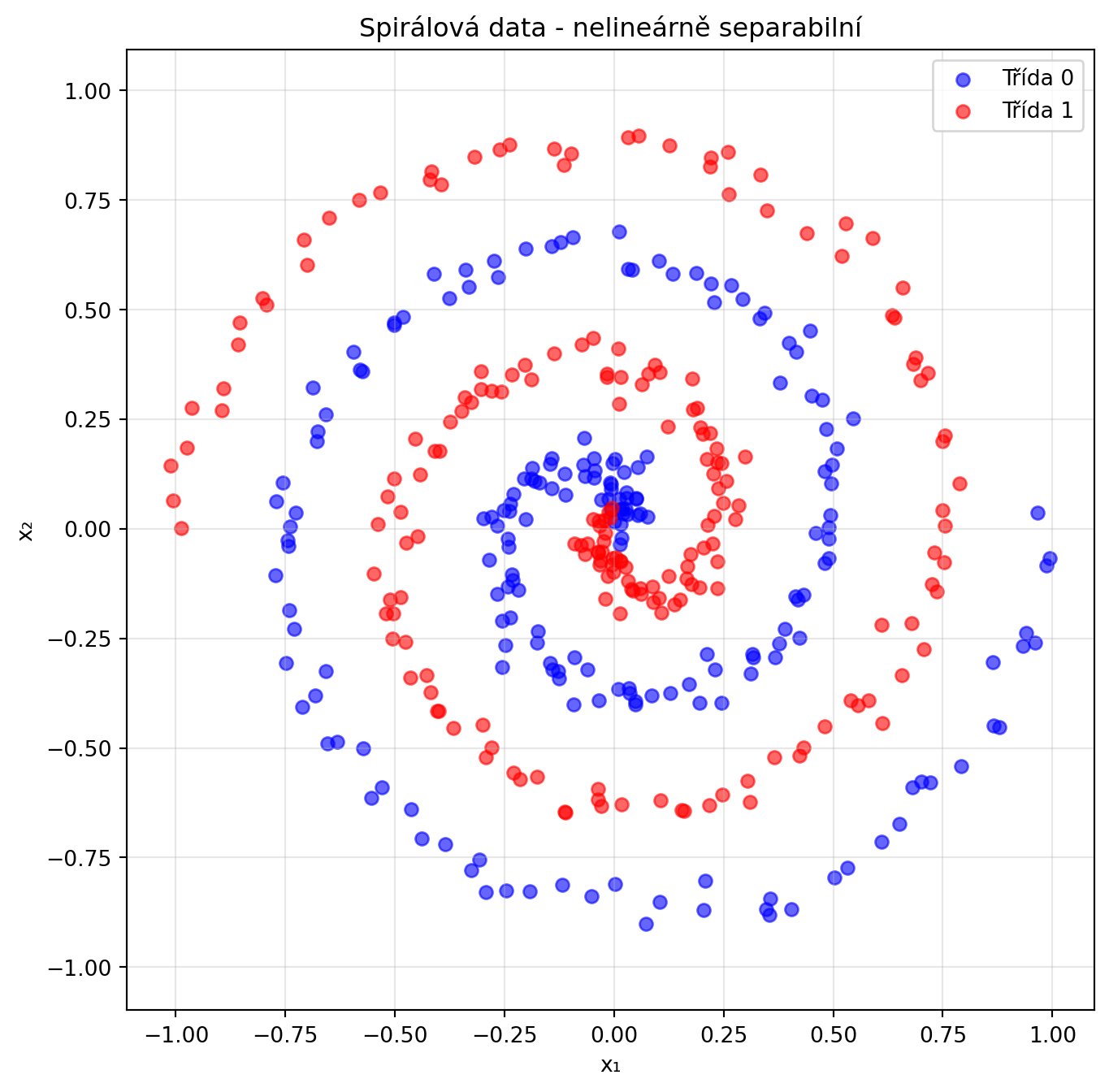
plt.title('Spirálová data - nelineárně separabilní')
plt.legend()
plt.axis('equal')
plt.grid(True, alpha=0.3)
plt.show()
```
```{python}
# Trénování MLP
import numpy as np
import matplotlib.pyplot as plt
torch.manual_seed(42)
X_tensor = torch.FloatTensor(X_spiral)
y_tensor = torch.FloatTensor(y_spiral).unsqueeze(1)
# Model
model = nn.Sequential(
nn.Linear(2, 32),
nn.ReLU(),
nn.Linear(32, 16),
nn.ReLU(),
nn.Linear(16, 1),
nn.Sigmoid()
)
criterion = nn.BCELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
# Trénink
losses = []
accuracies = []
for epoch in range(500):
# Forward
y_pred = model(X_tensor)
loss = criterion(y_pred, y_tensor)
# Backward
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Metriky
with torch.no_grad():
acc = ((y_pred > 0.5) == y_tensor).float().mean()
losses.append(loss.item())
accuracies.append(acc.item())
if (epoch + 1) % 100 == 0:
print(f"Epocha {epoch+1}: Loss = {loss.item():.4f}, Accuracy = {acc.item():.2%}")
# Vizualizace výsledků
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# Trénink
axes[0].plot(losses, 'b-', lw=2)
axes[0].set_xlabel('Epocha')
axes[0].set_ylabel('Loss')
axes[0].set_title('Průběh tréninku')
axes[0].grid(True, alpha=0.3)
axes[1].plot(accuracies, 'g-', lw=2)
axes[1].set_xlabel('Epocha')
axes[1].set_ylabel('Accuracy')
axes[1].set_title('Přesnost')
axes[1].set_ylim(0, 1.05)
axes[1].grid(True, alpha=0.3)
# Rozhodovací hranice
xx, yy = np.meshgrid(np.linspace(-1.5, 1.5, 200), np.linspace(-1.5, 1.5, 200))
grid = torch.FloatTensor(np.c_[xx.ravel(), yy.ravel()])
with torch.no_grad():
Z = model(grid).numpy().reshape(xx.shape)
axes[2].contourf(xx, yy, Z, levels=[0, 0.5, 1], colors=['blue', 'red'], alpha=0.3)
axes[2].contour(xx, yy, Z, levels=[0.5], colors='green', linewidths=2)
axes[2].scatter(X_spiral[y_spiral==0, 0], X_spiral[y_spiral==0, 1], c='blue', alpha=0.6, s=10)
axes[2].scatter(X_spiral[y_spiral==1, 0], X_spiral[y_spiral==1, 1], c='red', alpha=0.6, s=10)
axes[2].set_xlabel('x₁')
axes[2].set_ylabel('x₂')
axes[2].set_title(f'Naučená hranice (acc: {accuracies[-1]:.0%})')
axes[2].axis('equal')
plt.tight_layout()
plt.show()
```
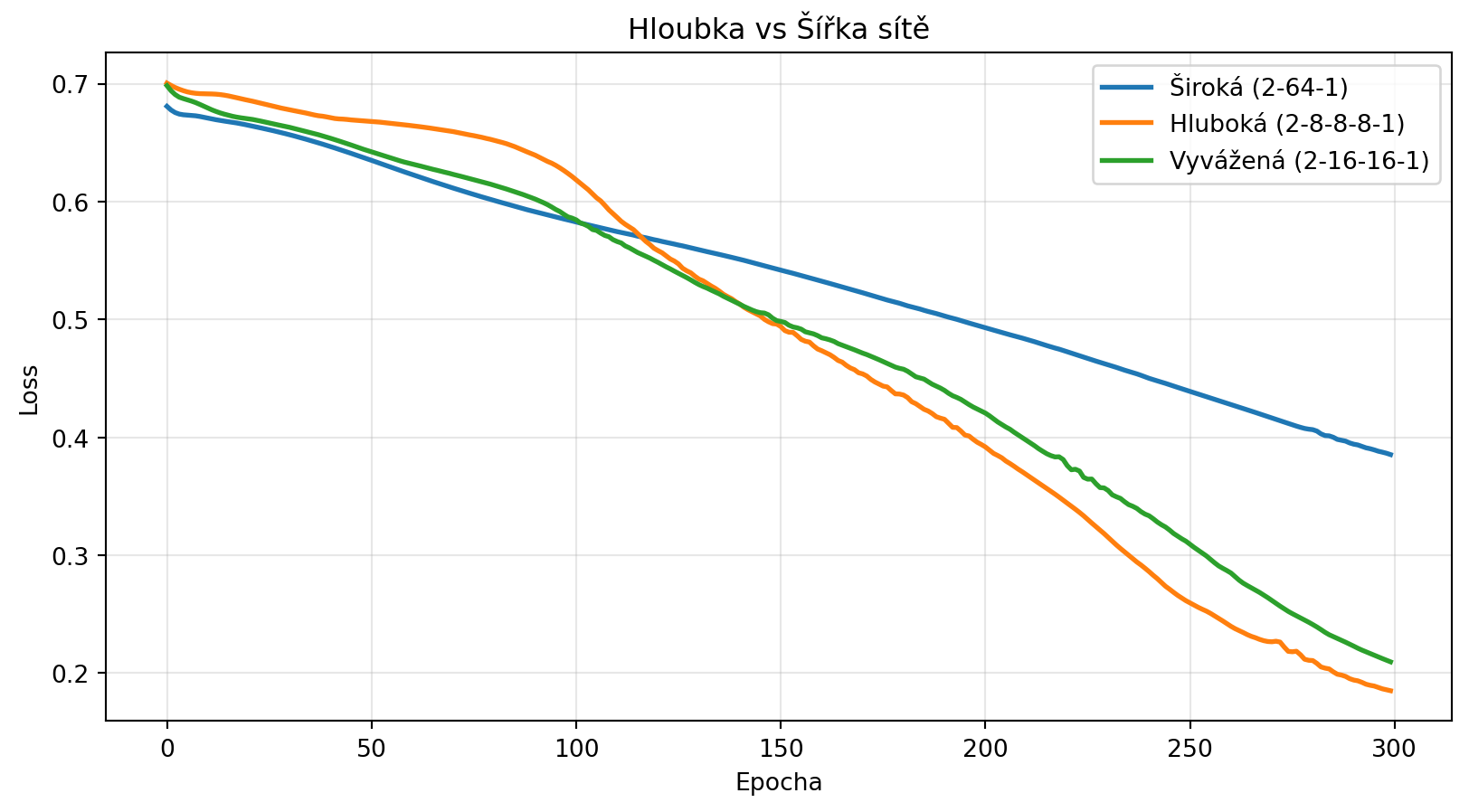
## Hloubka vs šířka
Jaká architektura je lepší - více neuronů v jedné vrstvě, nebo více vrstev?
```{python}
# Porovnání architektur se stejným počtem parametrů
import matplotlib.pyplot as plt
def count_params(layer_sizes):
total = 0
for i in range(len(layer_sizes) - 1):
total += layer_sizes[i] * layer_sizes[i+1] + layer_sizes[i+1]
return total
architectures = {
'Široká (2-64-1)': [2, 64, 1],
'Hluboká (2-8-8-8-1)': [2, 8, 8, 8, 1],
'Vyvážená (2-16-16-1)': [2, 16, 16, 1],
}
print("Porovnání architektur:")
print("-" * 50)
for name, arch in architectures.items():
params = count_params(arch)
print(f"{name}: {params} parametrů")
# Trénování a porovnání
results = {}
for name, arch in architectures.items():
torch.manual_seed(42)
# Vytvoření modelu
layers = []
for i in range(len(arch) - 1):
layers.append(nn.Linear(arch[i], arch[i+1]))
if i < len(arch) - 2:
layers.append(nn.ReLU())
layers.append(nn.Sigmoid())
model = nn.Sequential(*layers)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
losses = []
for epoch in range(300):
y_pred = model(X_tensor)
loss = criterion(y_pred, y_tensor)
optimizer.zero_grad()
loss.backward()
optimizer.step()
losses.append(loss.item())
results[name] = losses
# Vizualizace
plt.figure(figsize=(10, 5))
for name, losses in results.items():
plt.plot(losses, label=name, lw=2)
plt.xlabel('Epocha')
plt.ylabel('Loss')
plt.title('Hloubka vs Šířka sítě')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
## Regularizace: Prevence přetrénování
MLP může snadno přetrénovat (overfit) na trénovací data. Používáme různé techniky regularizace:
### Dropout
```{python}
# MLP s Dropout
class MLPWithDropout(nn.Module):
def __init__(self, dropout_rate=0.5):
super().__init__()
self.network = nn.Sequential(
nn.Linear(2, 32),
nn.ReLU(),
nn.Dropout(dropout_rate), # Náhodně "vypíná" neurony
nn.Linear(32, 16),
nn.ReLU(),
nn.Dropout(dropout_rate),
nn.Linear(16, 1),
nn.Sigmoid()
)
def forward(self, x):
return self.network(x)
# Demonstrace Dropout
model = MLPWithDropout(dropout_rate=0.5)
x = torch.randn(1, 2)
print("Dropout demonstrace:")
model.train() # Dropout aktivní
outputs_train = [model(x).item() for _ in range(5)]
print(f"Trénink (různé výstupy): {[f'{o:.4f}' for o in outputs_train]}")
model.eval() # Dropout neaktivní
outputs_eval = [model(x).item() for _ in range(5)]
print(f"Evaluace (stejné výstupy): {[f'{o:.4f}' for o in outputs_eval]}")
```
### Batch Normalization
```{python}
class MLPWithBatchNorm(nn.Module):
def __init__(self):
super().__init__()
self.network = nn.Sequential(
nn.Linear(2, 32),
nn.BatchNorm1d(32), # Normalizuje aktivace
nn.ReLU(),
nn.Linear(32, 16),
nn.BatchNorm1d(16),
nn.ReLU(),
nn.Linear(16, 1),
nn.Sigmoid()
)
def forward(self, x):
return self.network(x)
print("Batch Normalization:")
print("- Normalizuje aktivace na průměr 0 a variance 1")
print("- Stabilizuje trénink")
print("- Umožňuje větší learning rate")
print("- Má mírný regularizační efekt")
```
## Řešené příklady
### Příklad 1: Ruční výpočet forward pass
**Zadání**: Pro síť 2→2→1 s vahami $W^{(1)} = \begin{bmatrix} 0.5 & -0.3 \\ 0.2 & 0.8 \end{bmatrix}$, $b^{(1)} = [0.1, -0.1]$, $W^{(2)} = [0.6, -0.4]$, $b^{(2)} = 0.2$ a vstupem $x = [1, 2]$ spočítejte výstup (ReLU, pak sigmoid).
**Řešení**:
```{python}
# Definice sítě
import numpy as np
W1 = np.array([[0.5, -0.3],
[0.2, 0.8]])
b1 = np.array([0.1, -0.1])
W2 = np.array([[0.6, -0.4]])
b2 = np.array([0.2])
x = np.array([1, 2])
# Vrstva 1
print("Vrstva 1 (ReLU):")
z1 = W1 @ x + b1
print(f" z₁ = W₁·x + b₁ = {W1} @ {x} + {b1}")
print(f" = {z1}")
a1 = np.maximum(0, z1)
print(f" a₁ = ReLU(z₁) = {a1}")
# Vrstva 2
print("\nVrstva 2 (Sigmoid):")
z2 = W2 @ a1 + b2
print(f" z₂ = W₂·a₁ + b₂ = {W2} @ {a1} + {b2}")
print(f" = {z2}")
a2 = 1 / (1 + np.exp(-z2))
print(f" a₂ = σ(z₂) = {a2[0]:.4f}")
print(f"\nVýstup sítě: {a2[0]:.4f}")
```
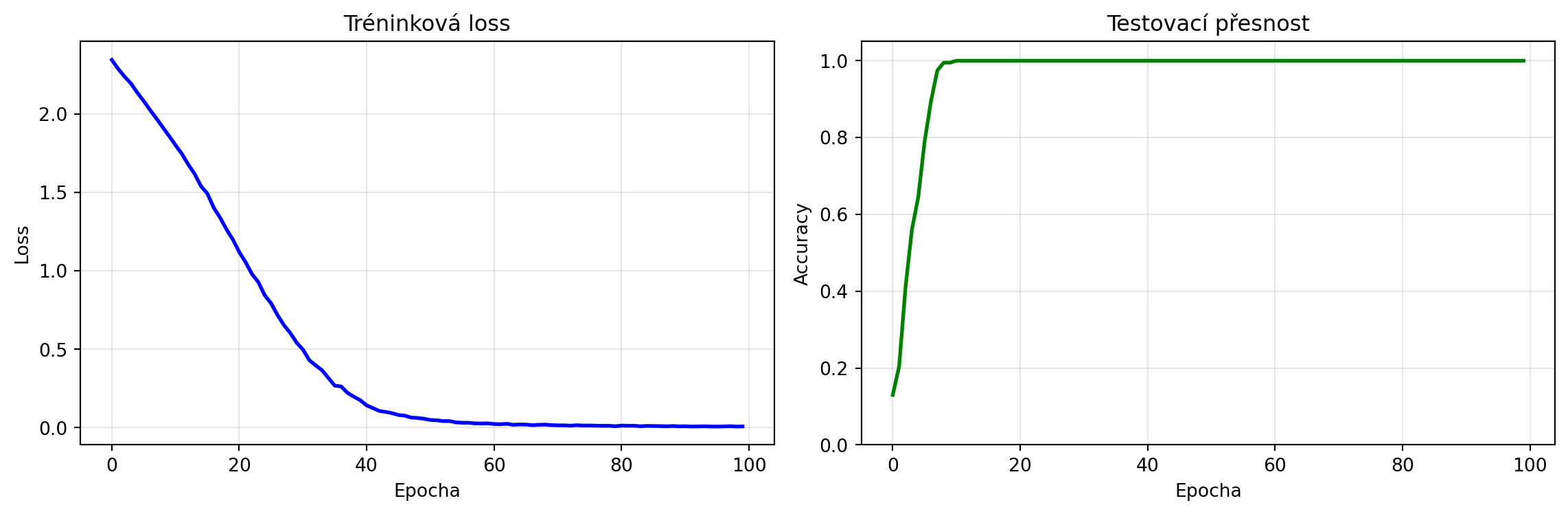
### Příklad 2: Klasifikace MNIST číslic
**Zadání**: Natrénujte MLP pro klasifikaci ručně psaných číslic.
**Řešení**:
```{python}
# Vytvoříme syntetická data pro klasifikaci (simulace číslic)
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
n_samples = 1000
n_features = 64
n_classes = 10
# Generujeme data - každá třída má jiný centroid
X_all = []
y_all = []
for c in range(n_classes):
# Náhodný centroid pro třídu
centroid = np.random.randn(n_features) * 2
# Vzorky kolem centroidu
X_class = centroid + np.random.randn(n_samples // n_classes, n_features) * 0.5
X_all.append(X_class)
y_all.extend([c] * (n_samples // n_classes))
X = np.vstack(X_all)
y = np.array(y_all)
# Promíchání dat
indices = np.random.permutation(len(X))
X, y = X[indices], y[indices]
# Rozdělení na train/test
split = int(0.8 * len(X))
X_train, X_test = X[:split], X[split:]
y_train, y_test = y[:split], y[split:]
# Normalizace (bez sklearn)
mean = X_train.mean(axis=0)
std = X_train.std(axis=0) + 1e-8
X_train = (X_train - mean) / std
X_test = (X_test - mean) / std
# Převod na tensory
X_train_t = torch.FloatTensor(X_train)
y_train_t = torch.LongTensor(y_train)
X_test_t = torch.FloatTensor(X_test)
y_test_t = torch.LongTensor(y_test)
# Model
class DigitClassifier(nn.Module):
def __init__(self):
super().__init__()
self.network = nn.Sequential(
nn.Linear(64, 128),
nn.ReLU(),
nn.Dropout(0.3),
nn.Linear(128, 64),
nn.ReLU(),
nn.Dropout(0.3),
nn.Linear(64, 10) # 10 tříd
)
def forward(self, x):
return self.network(x)
torch.manual_seed(42)
model = DigitClassifier()
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
# Trénink
train_losses = []
test_accs = []
for epoch in range(100):
model.train()
optimizer.zero_grad()
output = model(X_train_t)
loss = criterion(output, y_train_t)
loss.backward()
optimizer.step()
train_losses.append(loss.item())
# Evaluace
model.eval()
with torch.no_grad():
test_output = model(X_test_t)
test_pred = test_output.argmax(dim=1)
test_acc = (test_pred == y_test_t).float().mean()
test_accs.append(test_acc.item())
print(f"Finální přesnost na test datech: {test_accs[-1]:.2%}")
# Vizualizace
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.plot(train_losses, 'b-', lw=2)
ax1.set_xlabel('Epocha')
ax1.set_ylabel('Loss')
ax1.set_title('Tréninková loss')
ax1.grid(True, alpha=0.3)
ax2.plot(test_accs, 'g-', lw=2)
ax2.set_xlabel('Epocha')
ax2.set_ylabel('Accuracy')
ax2.set_title('Testovací přesnost')
ax2.set_ylim(0, 1.05)
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
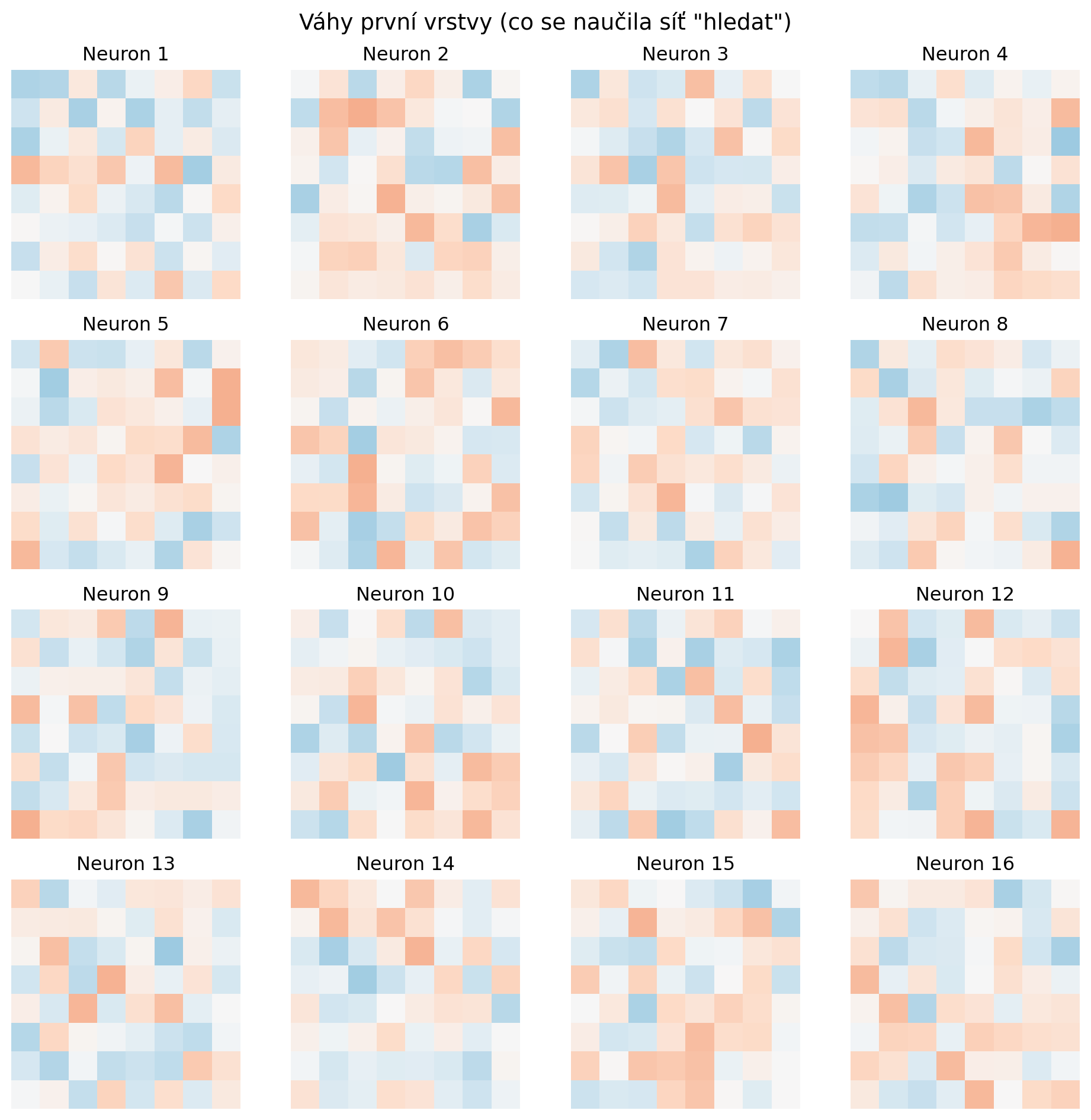
### Příklad 3: Vizualizace naučených features
**Zadání**: Vizualizujte, co se naučila první vrstva sítě.
**Řešení**:
```{python}
# Váhy první vrstvy
import matplotlib.pyplot as plt
weights = model.network[0].weight.data.numpy() # (128, 64)
# Vybereme prvních 16 neuronů
fig, axes = plt.subplots(4, 4, figsize=(10, 10))
for i, ax in enumerate(axes.flatten()):
if i < 16:
# Každý neuron má 64 vah (8x8 obrázek)
w = weights[i].reshape(8, 8)
ax.imshow(w, cmap='RdBu', vmin=-0.5, vmax=0.5)
ax.axis('off')
ax.set_title(f'Neuron {i+1}')
plt.suptitle('Váhy první vrstvy (co se naučila síť "hledat")', fontsize=14)
plt.tight_layout()
plt.show()
```
## Cvičení
::: {.callout-note icon=false}
## Cvičení 1: XOR
Natrénujte MLP pro XOR s minimálním počtem neuronů ve skryté vrstvě. Kolik jich stačí?
:::
::: {.callout-note icon=false}
## Cvičení 2: Regrese
Použijte MLP pro regresní úlohu - aproximaci funkce $y = \sin(x)$ na intervalu $[0, 2\pi]$.
:::
::: {.callout-note icon=false}
## Cvičení 3: Hyperparametr tuning
Experimentujte s různými kombinacemi:
- Počet vrstev (1-4)
- Počet neuronů (8, 16, 32, 64)
- Aktivační funkce (ReLU, Tanh, LeakyReLU)
Najděte nejlepší architekturu pro spirálová data.
:::
::: {.callout-note icon=false}
## Cvičení 4: Regularizace
Porovnejte trénink s a bez Dropout na komplexních datech. Ukažte, že Dropout pomáhá proti přetrénování.
:::
::: {.callout-note icon=false}
## Cvičení 5: Inicializace vah
Porovnejte různé inicializace vah (Xavier, He, normální rozdělení). Která vede k nejrychlejší konvergenci?
:::
## Shrnutí
::: {.callout-tip}
## Co jsme se naučili
1. **MLP** skládá více vrstev neuronů pro řešení nelineárních problémů
2. **Forward pass**: postupné aplikování vrstev $\mathbf{a}^{(l)} = \sigma(\mathbf{W}^{(l)} \mathbf{a}^{(l-1)} + \mathbf{b}^{(l)})$
3. **Hloubka vs šířka**: hlubší sítě mohou být efektivnější, ale jsou těžší na trénování
4. **Regularizace**: Dropout a Batch Normalization pomáhají proti přetrénování
5. **PyTorch**: `nn.Sequential` a `nn.Linear` pro snadnou definici sítí
6. MLP je **univerzální aproximátor** - může aproximovat libovolnou spojitou funkci
:::
::: {.callout-important}
## Klíčové pojmy
- **Fully connected / Dense vrstva**: Každý neuron je spojen se všemi v předchozí vrstvě
- **Skrytá vrstva**: Vrstvy mezi vstupem a výstupem
- **Aktivační funkce**: ReLU, Sigmoid, Tanh - vnáší nelinearitu
- **Dropout**: Regularizace náhodným "vypínáním" neuronů
- **Batch Normalization**: Normalizace aktivací pro stabilnější trénink
:::
V další kapitole se podíváme na **backpropagation** - klíčový algoritmus pro výpočet gradientů a trénování neuronových sítí.