import sympy as sp
x = sp.Symbol('x')
f = x**3 + 2*x**2 - 5*x + 3
derivace = sp.diff(f, x)
print(f"f(x) = {f}")
print(f"f'(x) = {derivace}")f(x) = x**3 + 2*x**2 - 5*x + 3
f'(x) = 3*x**2 + 4*x - 5V minulých kapitolách jsme se naučili derivovat ručně pomocí pravidel. Také jsme viděli, že derivace můžeme aproximovat numericky pomocí malého \(h\):
\[f'(x) \approx \frac{f(x+h) - f(x)}{h}\]
Neuronové sítě ale můžou mít miliony parametrů a potřebujeme spočítat parciální derivace podle každého z nich. Ruční derivování je nemožné a numerická aproximace je příliš pomalá a nepřesná.
Řešením je automatická derivace (automatic differentiation, zkráceně autodiff nebo autograd). Tato technika:
Pochopení automatické derivace je klíčové pro pochopení, jak se neuronové sítě učí. V této kapitole se podíváme pod kapotu PyTorche a dalších frameworků pro strojové učení.
To je to, co jsme dělali ručně - aplikujeme pravidla jako “derivace \(x^n\) je \(nx^{n-1}\)”:
import sympy as sp
x = sp.Symbol('x')
f = x**3 + 2*x**2 - 5*x + 3
derivace = sp.diff(f, x)
print(f"f(x) = {f}")
print(f"f'(x) = {derivace}")f(x) = x**3 + 2*x**2 - 5*x + 3
f'(x) = 3*x**2 + 4*x - 5Výhody: Přesný analytický výsledek.
Nevýhody: Výraz může explodovat do obrovských formulí. Pro složité funkce je to neefektivní.
Aproximace pomocí malého kroku:
def numericka_derivace(f, x, h=1e-7):
return (f(x + h) - f(x)) / h
def f(x):
return x**3 + 2*x**2 - 5*x + 3
# Přesná derivace v bodě x=2 je 3*4 + 4*2 - 5 = 15
print(f"Numerická derivace v x=2: {numericka_derivace(f, 2):.10f}")
print(f"Přesná hodnota: 15.0")Numerická derivace v x=2: 15.0000007793
Přesná hodnota: 15.0Výhody: Funguje pro jakoukoli funkci.
Nevýhody: Pouze aproximace, může být nepřesné nebo numericky nestabilní.
Automatická derivace kombinuje nejlepší z obou světů:
Automatická derivace není symbolická ani numerická derivace. Je to samostatná technika, která sleduje výpočet a aplikuje řetízkové pravidlo na jednotlivé kroky.
Klíčem k pochopení autodiff je výpočetní graf (computational graph). Každý matematický výraz můžeme rozložit na posloupnost jednoduchých operací.
Vezměme funkci \(f(x, y) = (x + y) \cdot (x - y)\).
Můžeme ji rozložit na kroky:
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import numpy as np
fig, ax = plt.subplots(figsize=(10, 6))
# Uzly grafu
nodes = {
'x': (0, 2),
'y': (0, 0),
'a': (2, 2.5),
'b': (2, -0.5),
'f': (4, 1)
}
# Kreslení uzlů
for name, (px, py) in nodes.items():
if name in ['x', 'y']:
color = '#3498db'
label = name
elif name == 'f':
color = '#e74c3c'
label = f"f = a·b"
elif name == 'a':
color = '#2ecc71'
label = "a = x+y"
else:
color = '#2ecc71'
label = "b = x-y"
circle = plt.Circle((px, py), 0.4, color=color, ec='black', lw=2)
ax.add_patch(circle)
ax.annotate(label, (px, py), ha='center', va='center', fontsize=11, fontweight='bold')
# Hrany
edges = [
('x', 'a'), ('y', 'a'),
('x', 'b'), ('y', 'b'),
('a', 'f'), ('b', 'f')
]
for start, end in edges:
x1, y1 = nodes[start]
x2, y2 = nodes[end]
# Zkrátíme šipku, aby nezasahovala do kruhu
dx, dy = x2 - x1, y2 - y1
length = np.sqrt(dx**2 + dy**2)
dx, dy = dx/length, dy/length
ax.annotate('', xy=(x2 - 0.45*dx, y2 - 0.45*dy),
xytext=(x1 + 0.45*dx, y1 + 0.45*dy),
arrowprops=dict(arrowstyle='->', color='black', lw=1.5))
ax.set_xlim(-1, 5.5)
ax.set_ylim(-1.5, 3.5)
ax.set_aspect('equal')
ax.axis('off')
ax.set_title('Výpočetní graf pro f(x,y) = (x+y)(x-y)', fontsize=14)
plt.tight_layout()
plt.show()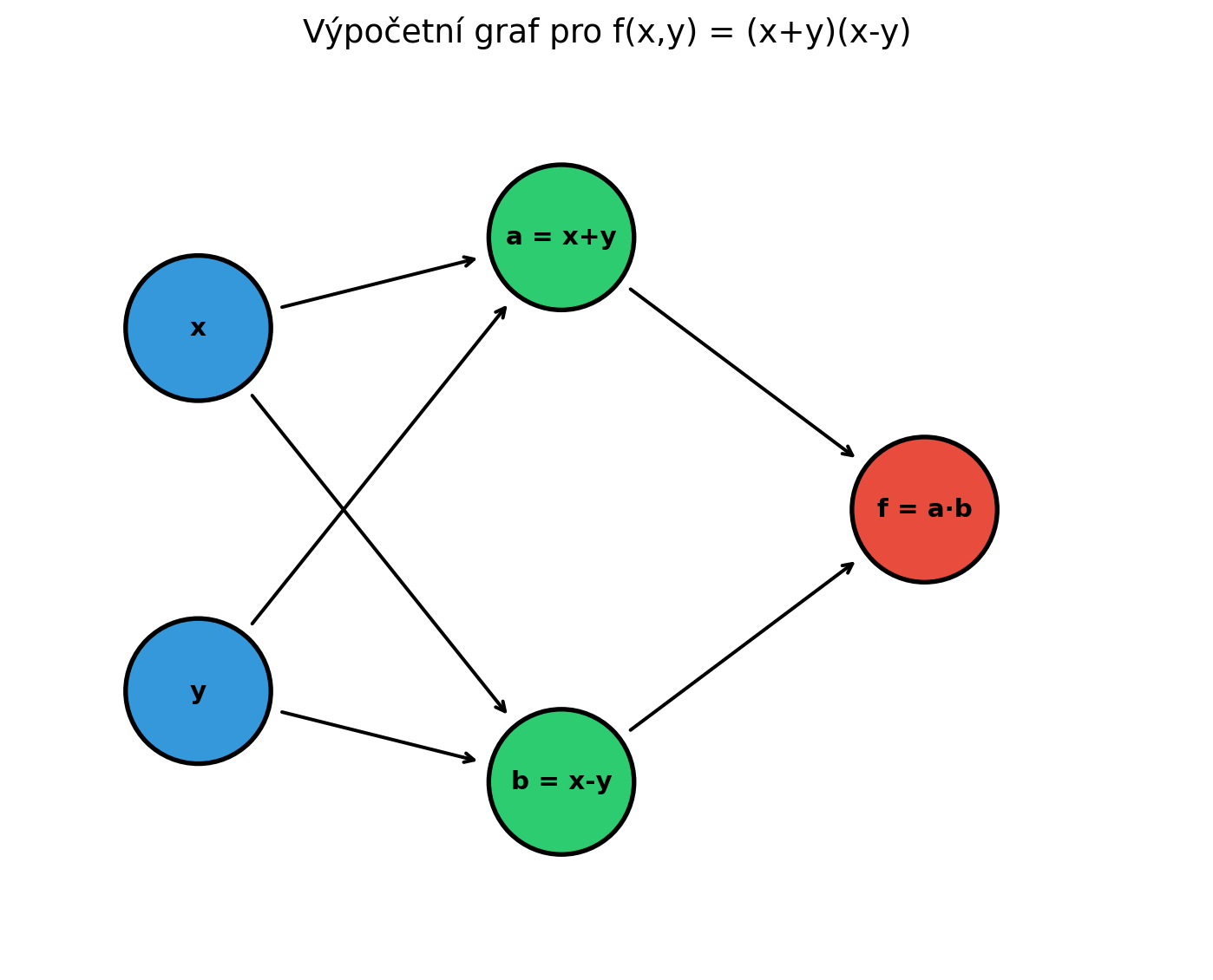
Při výpočtu hodnoty funkce procházíme graf zleva doprava:
# Konkrétní hodnoty
x = 3
y = 2
# Dopředný průchod
a = x + y # a = 5
b = x - y # b = 1
f = a * b # f = 5
print(f"Vstup: x = {x}, y = {y}")
print(f"Krok 1: a = x + y = {a}")
print(f"Krok 2: b = x - y = {b}")
print(f"Krok 3: f = a * b = {f}")
print(f"\nVýsledek: f(3, 2) = {f}")Vstup: x = 3, y = 2
Krok 1: a = x + y = 5
Krok 2: b = x - y = 1
Krok 3: f = a * b = 5
Výsledek: f(3, 2) = 5Teď přichází kouzlo automatické derivace. Chceme spočítat \(\frac{\partial f}{\partial x}\) a \(\frac{\partial f}{\partial y}\).
Pro každý uzel spočítáme, jak změna tohoto uzlu ovlivní výstup. Postupujeme zprava doleva - od výstupu ke vstupům.
# Hodnoty z dopředného průchodu
x, y = 3, 2
a = x + y # = 5
b = x - y # = 1
f = a * b # = 5
# Zpětný průchod
# Začínáme s df/df = 1
df_df = 1
# Derivace f = a * b
df_da = b * df_df # = 1 * 1 = 1
df_db = a * df_df # = 5 * 1 = 5
# Derivace a = x + y
da_dx = 1
da_dy = 1
# Derivace b = x - y
db_dx = 1
db_dy = -1
# Celkové derivace (řetízkové pravidlo)
df_dx = df_da * da_dx + df_db * db_dx # = 1*1 + 5*1 = 6
df_dy = df_da * da_dy + df_db * db_dy # = 1*1 + 5*(-1) = -4
print("Zpětný průchod:")
print(f"df/df = {df_df}")
print(f"df/da = b = {df_da}")
print(f"df/db = a = {df_db}")
print(f"\nCelkové gradienty:")
print(f"∂f/∂x = {df_dx}")
print(f"∂f/∂y = {df_dy}")Zpětný průchod:
df/df = 1
df/da = b = 1
df/db = a = 5
Celkové gradienty:
∂f/∂x = 6
∂f/∂y = -4Můžeme ověřit analyticky. Pro \(f(x,y) = (x+y)(x-y) = x^2 - y^2\):
Při zpětném průchodu (backward mode) spočítáme gradienty podle všech vstupů najednou v jednom průchodu. To je ideální pro neuronové sítě, které mají miliony parametrů ale jen jeden skalární výstup (loss).
Existují dva způsoby, jak automaticky derivovat:
Počítáme derivaci jednoho vstupu současně s hodnotou funkce:
def forward_mode(x, y, derive_by='x'):
"""Forward mode autodiff - sleduje derivaci podle jedné proměnné."""
if derive_by == 'x':
# x = x, dx/dx = 1
# y = y, dy/dx = 0
val_x, grad_x = x, 1
val_y, grad_y = y, 0
else:
val_x, grad_x = x, 0
val_y, grad_y = y, 1
# a = x + y
val_a = val_x + val_y
grad_a = grad_x + grad_y
# b = x - y
val_b = val_x - val_y
grad_b = grad_x - grad_y
# f = a * b
val_f = val_a * val_b
grad_f = grad_a * val_b + val_a * grad_b # Pravidlo pro součin
return val_f, grad_f
x, y = 3, 2
val, df_dx = forward_mode(x, y, derive_by='x')
_, df_dy = forward_mode(x, y, derive_by='y')
print(f"f({x}, {y}) = {val}")
print(f"∂f/∂x = {df_dx}")
print(f"∂f/∂y = {df_dy}")f(3, 2) = 5
∂f/∂x = 6
∂f/∂y = -4Nevýhoda: Pro každý vstup musíme projít celý graf znovu.
Spočítáme hodnotu dopředu, pak gradienty všech vstupů v jednom zpětném průchodu:
def backward_mode(x, y):
"""Backward mode autodiff - jeden průchod pro všechny gradienty."""
# Forward pass - uložíme mezivýsledky
a = x + y
b = x - y
f = a * b
# Backward pass - od výstupu ke vstupům
df = 1 # df/df
# f = a * b -> df/da = b, df/db = a
da = b * df
db = a * df
# a = x + y -> da/dx = 1, da/dy = 1
# b = x - y -> db/dx = 1, db/dy = -1
dx = da * 1 + db * 1
dy = da * 1 + db * (-1)
return f, dx, dy
x, y = 3, 2
f, df_dx, df_dy = backward_mode(x, y)
print(f"f({x}, {y}) = {f}")
print(f"∂f/∂x = {df_dx}")
print(f"∂f/∂y = {df_dy}")f(3, 2) = 5
∂f/∂x = 6
∂f/∂y = -4Neuronové sítě mají miliony parametrů (vstupů) a jeden loss (výstup), proto se používá backward mode - tedy backpropagation.
PyTorch implementuje backward mode autodiff velmi elegantně. Stačí nastavit requires_grad=True a PyTorch bude sledovat všechny operace.
import torch
# Vytvoříme tensory se sledováním gradientů
x = torch.tensor(3.0, requires_grad=True)
y = torch.tensor(2.0, requires_grad=True)
# Dopředný průchod - PyTorch si pamatuje operace
a = x + y
b = x - y
f = a * b
print(f"f = {f.item()}")
# Zpětný průchod - jeden příkaz!
f.backward()
# Gradienty jsou automaticky spočítány
print(f"∂f/∂x = {x.grad.item()}")
print(f"∂f/∂y = {y.grad.item()}")f = 5.0
∂f/∂x = 6.0
∂f/∂y = -4.0# Reset gradientů
import numpy as np
x = torch.tensor(2.0, requires_grad=True)
# Složená funkce: f(x) = sin(x^2) * exp(-x)
f = torch.sin(x**2) * torch.exp(-x)
print(f"x = {x.item()}")
print(f"f(x) = {f.item():.6f}")
# Spočítáme derivaci
f.backward()
print(f"f'(x) = {x.grad.item():.6f}")
# Ověření analyticky: f'(x) = 2x*cos(x^2)*exp(-x) - sin(x^2)*exp(-x)
analyticka = (2*2*np.cos(4)*np.exp(-2) - np.sin(4)*np.exp(-2))
print(f"Analyticky: {analyticka:.6f}")x = 2.0
f(x) = -0.102422
f'(x) = -0.251422
Analyticky: -0.251422# Matice vah
W = torch.tensor([[1.0, 2.0],
[3.0, 4.0]], requires_grad=True)
# Vstupní vektor
x = torch.tensor([1.0, 1.0])
# Dopředný průchod: y = Wx, pak součet prvků
y = W @ x
loss = y.sum() # Skalár pro backward
print(f"W:\n{W}")
print(f"x: {x}")
print(f"y = Wx: {y}")
print(f"loss = sum(y): {loss.item()}")
# Zpětný průchod
loss.backward()
print(f"\n∂loss/∂W:\n{W.grad}")W:
tensor([[1., 2.],
[3., 4.]], requires_grad=True)
x: tensor([1., 1.])
y = Wx: tensor([3., 7.], grad_fn=<MvBackward0>)
loss = sum(y): 10.0
∂loss/∂W:
tensor([[1., 1.],
[1., 1.]])PyTorch vytváří výpočetní graf dynamicky během dopředného průchodu:
x = torch.tensor(2.0, requires_grad=True)
y = torch.tensor(3.0, requires_grad=True)
# Každá operace vytvoří uzel v grafu
z = x * y
w = z + x
result = w ** 2
# Můžeme vidět funkci, která vytvořila tensor
print(f"z = x * y, grad_fn: {z.grad_fn}")
print(f"w = z + x, grad_fn: {w.grad_fn}")
print(f"result = w^2, grad_fn: {result.grad_fn}")
# Backward projde graf zpětně
result.backward()
print(f"\n∂result/∂x = {x.grad.item()}")
print(f"∂result/∂y = {y.grad.item()}")z = x * y, grad_fn: <MulBackward0 object at 0xeb89e56b0af0>
w = z + x, grad_fn: <AddBackward0 object at 0xeb89e56b06d0>
result = w^2, grad_fn: <PowBackward0 object at 0xeb89e56b0af0>
∂result/∂x = 64.0
∂result/∂y = 32.0PyTorch přičítá gradienty k existujícím hodnotám. Před novým backward() je nutné gradienty vynulovat:
x.grad.zero_() # Vynuluje gradientToto je důležité při trénování v cyklech!
Spojme automatickou derivaci s optimalizací:
import torch
import matplotlib.pyplot as plt
# Chceme najít minimum funkce f(x) = (x-3)^2 + 1
# Minimum je v x = 3
x = torch.tensor(0.0, requires_grad=True) # Začínáme v x=0
learning_rate = 0.1
historie = [x.item()]
for krok in range(20):
# Dopředný průchod
f = (x - 3)**2 + 1
# Zpětný průchod
f.backward()
# Gradient descent krok (bez sledování gradientů)
with torch.no_grad():
x -= learning_rate * x.grad
# Vynulování gradientu pro další iteraci
x.grad.zero_()
historie.append(x.item())
# Vizualizace
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
# Graf funkce s trajektorií
x_range = torch.linspace(-1, 5, 100)
y_range = (x_range - 3)**2 + 1
ax1.plot(x_range, y_range, 'b-', lw=2, label='f(x) = (x-3)² + 1')
ax1.plot(historie, [(h-3)**2 + 1 for h in historie], 'ro-', markersize=8, label='Gradient descent')
ax1.axvline(x=3, color='g', linestyle='--', alpha=0.5, label='Minimum (x=3)')
ax1.set_xlabel('x')
ax1.set_ylabel('f(x)')
ax1.legend()
ax1.set_title('Gradient Descent s PyTorch Autograd')
ax1.grid(True, alpha=0.3)
# Konvergence x
ax2.plot(historie, 'b.-', markersize=10)
ax2.axhline(y=3, color='g', linestyle='--', label='Optimum x=3')
ax2.set_xlabel('Iterace')
ax2.set_ylabel('x')
ax2.set_title('Konvergence k optimu')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print(f"Počáteční x: {historie[0]:.4f}")
print(f"Konečné x: {historie[-1]:.4f}")
print(f"Optimum: 3.0000")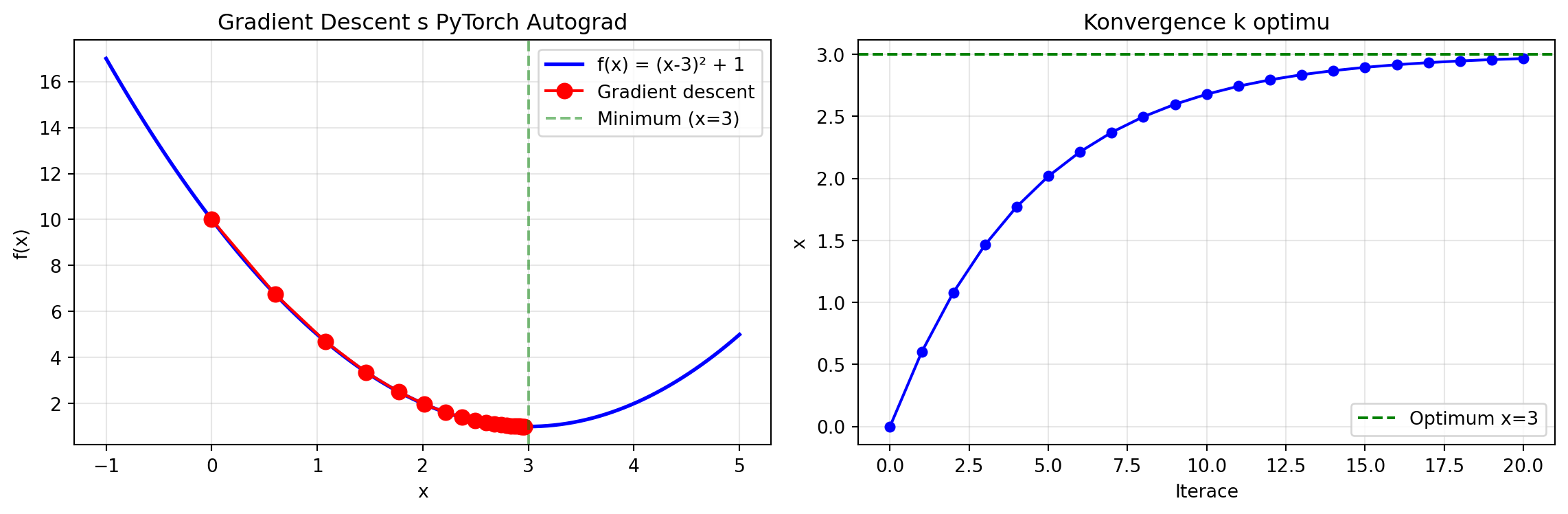
Počáteční x: 0.0000
Konečné x: 2.9654
Optimum: 3.0000Automatická derivace je srdcem tréninku neuronových sítí. Podívejme se na jednoduchý příklad:
import torch
import torch.nn as nn
# Jednoduchá síť: vstup (2) -> skrytá vrstva (3) -> výstup (1)
class JednoduchaSit(nn.Module):
def __init__(self):
super().__init__()
self.vrstva1 = nn.Linear(2, 3) # 2 vstupy, 3 neurony
self.vrstva2 = nn.Linear(3, 1) # 3 vstupy, 1 výstup
self.aktivace = nn.ReLU()
def forward(self, x):
x = self.vrstva1(x)
x = self.aktivace(x)
x = self.vrstva2(x)
return x
# Vytvoříme síť
sit = JednoduchaSit()
# Vstupní data
X = torch.tensor([[1.0, 2.0]]) # Jeden vzorek, 2 features
y_true = torch.tensor([[1.0]]) # Cílová hodnota
# Dopředný průchod
y_pred = sit(X)
print(f"Predikce: {y_pred.item():.4f}")
# Loss funkce
loss = (y_pred - y_true)**2
print(f"Loss: {loss.item():.4f}")
# Zpětný průchod - automaticky spočítá gradienty všech vah!
loss.backward()
# Podívejme se na gradienty
print("\nGradienty vah:")
for name, param in sit.named_parameters():
print(f"{name}: shape {param.grad.shape}")
print(f" grad = {param.grad}")Predikce: -0.3811
Loss: 1.9074
Gradienty vah:
vrstva1.weight: shape torch.Size([3, 2])
grad = tensor([[0.9438, 1.8877],
[0.0000, 0.0000],
[0.0327, 0.0653]])
vrstva1.bias: shape torch.Size([3])
grad = tensor([0.9438, 0.0000, 0.0327])
vrstva2.weight: shape torch.Size([1, 3])
grad = tensor([[-1.3765, 0.0000, -2.6923]])
vrstva2.bias: shape torch.Size([1])
grad = tensor([-2.7622])import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12, 8))
# Uzly sítě
layers = {
'input': [(0, 2), (0, 0)], # 2 vstupní neurony
'hidden': [(2, 3), (2, 1.5), (2, 0)], # 3 skryté neurony
'output': [(4, 1.5)] # 1 výstupní neuron
}
# Kreslení neuronů
for layer_name, positions in layers.items():
for i, (x, y) in enumerate(positions):
if layer_name == 'input':
color = '#3498db'
label = f'$x_{i+1}$'
elif layer_name == 'hidden':
color = '#2ecc71'
label = f'$h_{i+1}$'
else:
color = '#e74c3c'
label = '$\\hat{y}$'
circle = plt.Circle((x, y), 0.3, color=color, ec='black', lw=2)
ax.add_patch(circle)
ax.annotate(label, (x, y), ha='center', va='center', fontsize=14)
# Kreslení spojení
for x1, y1 in layers['input']:
for x2, y2 in layers['hidden']:
ax.plot([x1+0.3, x2-0.3], [y1, y2], 'gray', lw=0.5, alpha=0.5)
for x1, y1 in layers['hidden']:
for x2, y2 in layers['output']:
ax.plot([x1+0.3, x2-0.3], [y1, y2], 'gray', lw=0.5, alpha=0.5)
# Loss
ax.annotate('Loss', (5.5, 1.5), ha='center', va='center', fontsize=14,
bbox=dict(boxstyle='round', facecolor='#f39c12', edgecolor='black'))
ax.annotate('', xy=(5.1, 1.5), xytext=(4.35, 1.5),
arrowprops=dict(arrowstyle='->', color='black', lw=2))
# Šipky pro backprop
ax.annotate('', xy=(4.3, 0.5), xytext=(5.1, 0.5),
arrowprops=dict(arrowstyle='->', color='#e74c3c', lw=2))
ax.text(4.7, 0.2, 'Backprop', fontsize=10, color='#e74c3c', ha='center')
ax.set_xlim(-1, 7)
ax.set_ylim(-1, 4)
ax.set_aspect('equal')
ax.axis('off')
ax.set_title('Neuronová síť: Forward Pass → Loss → Backward Pass', fontsize=14)
# Legenda
ax.plot([], [], 'o', color='#3498db', markersize=15, label='Vstup')
ax.plot([], [], 'o', color='#2ecc71', markersize=15, label='Skrytá vrstva')
ax.plot([], [], 'o', color='#e74c3c', markersize=15, label='Výstup')
ax.legend(loc='upper right')
plt.tight_layout()
plt.show()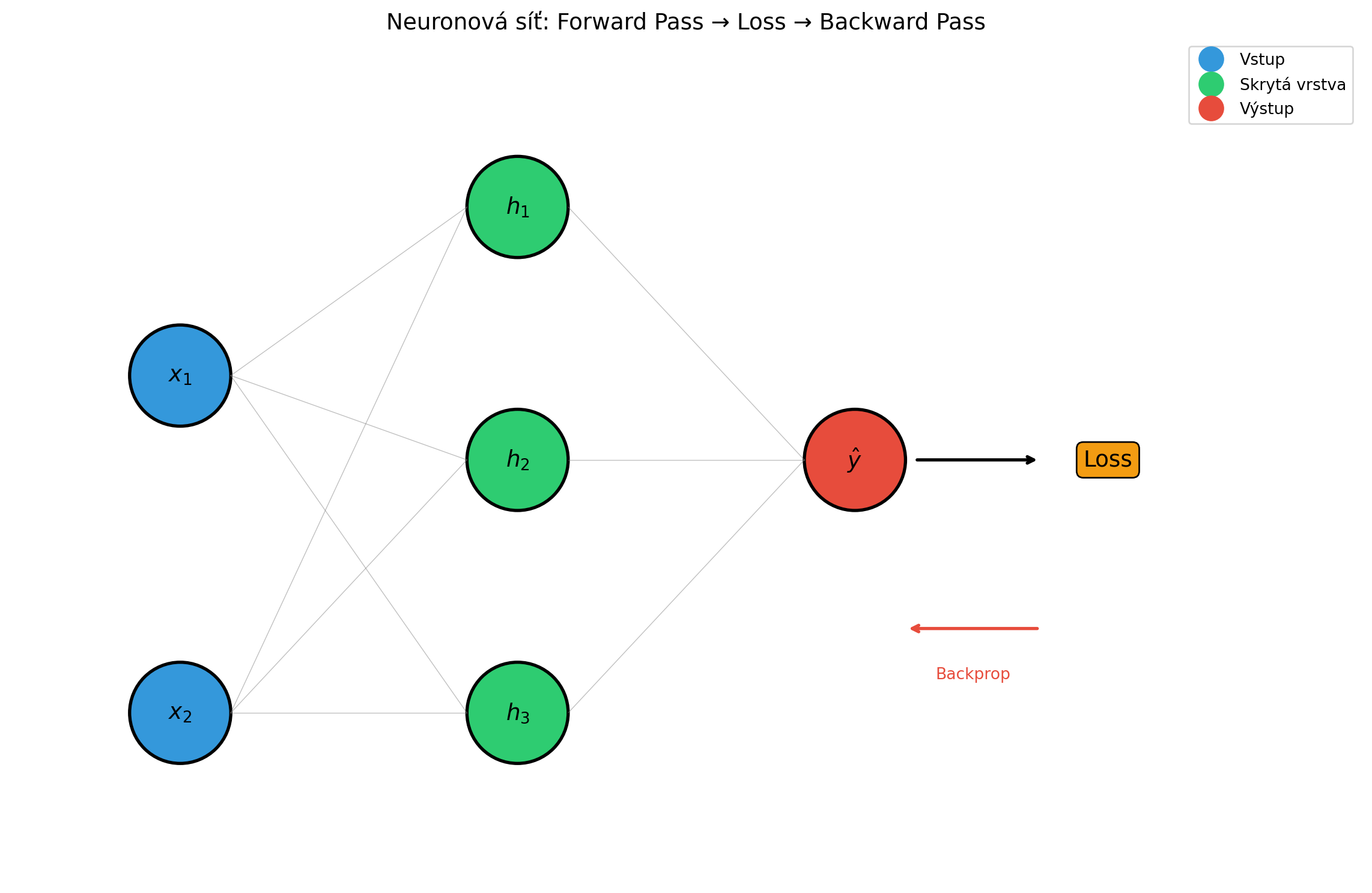
Zadání: Pro funkci \(f(x) = (x^2 + 1)^3\) spočítejte \(f'(2)\) pomocí výpočetního grafu.
Řešení:
Rozložíme na kroky: 1. \(a = x^2\) 2. \(b = a + 1\) 3. \(f = b^3\)
x = 2
# Forward pass
a = x**2 # a = 4
b = a + 1 # b = 5
f = b**3 # f = 125
print("Forward pass:")
print(f"a = x² = {a}")
print(f"b = a + 1 = {b}")
print(f"f = b³ = {f}")
# Backward pass
df_df = 1
df_db = 3 * b**2 * df_df # derivace b³ je 3b²
df_da = 1 * df_db # derivace a+1 podle a je 1
df_dx = 2 * x * df_da # derivace x² je 2x
print("\nBackward pass:")
print(f"df/df = {df_df}")
print(f"df/db = 3b² = {df_db}")
print(f"df/da = df/db * 1 = {df_da}")
print(f"df/dx = df/da * 2x = {df_dx}")
# Ověření analyticky: f'(x) = 3(x²+1)² * 2x = 6x(x²+1)²
analyticka = 6 * 2 * (4+1)**2
print(f"\nOvěření: 6x(x²+1)² = {analyticka}")Forward pass:
a = x² = 4
b = a + 1 = 5
f = b³ = 125
Backward pass:
df/df = 1
df/db = 3b² = 75
df/da = df/db * 1 = 75
df/dx = df/da * 2x = 300
Ověření: 6x(x²+1)² = 300Zadání: Spočítejte gradient funkce \(f(x, y, z) = xy + yz^2\) v bodě \((1, 2, 3)\).
Řešení:
x = torch.tensor(1.0, requires_grad=True)
y = torch.tensor(2.0, requires_grad=True)
z = torch.tensor(3.0, requires_grad=True)
f = x*y + y*z**2
print(f"f(1, 2, 3) = 1·2 + 2·3² = 2 + 18 = {f.item()}")
f.backward()
print(f"\n∂f/∂x = y = {x.grad.item()}") # y = 2
print(f"∂f/∂y = x + z² = {y.grad.item()}") # 1 + 9 = 10
print(f"∂f/∂z = 2yz = {z.grad.item()}") # 2·2·3 = 12f(1, 2, 3) = 1·2 + 2·3² = 2 + 18 = 20.0
∂f/∂x = y = 2.0
∂f/∂y = x + z² = 10.0
∂f/∂z = 2yz = 12.0Zadání: Najděte minimum funkce \(f(x, y) = (x-1)^2 + (y-2)^2\) pomocí gradient descent.
Řešení:
import numpy as np
import matplotlib.pyplot as plt
x = torch.tensor(0.0, requires_grad=True)
y = torch.tensor(0.0, requires_grad=True)
learning_rate = 0.1
historie_x = [x.item()]
historie_y = [y.item()]
for _ in range(50):
f = (x - 1)**2 + (y - 2)**2
f.backward()
with torch.no_grad():
x -= learning_rate * x.grad
y -= learning_rate * y.grad
x.grad.zero_()
y.grad.zero_()
historie_x.append(x.item())
historie_y.append(y.item())
print(f"Počátek: ({historie_x[0]:.4f}, {historie_y[0]:.4f})")
print(f"Konec: ({historie_x[-1]:.4f}, {historie_y[-1]:.4f})")
print(f"Optimum: (1.0000, 2.0000)")
# Vizualizace
fig, ax = plt.subplots(figsize=(8, 6))
# Kontury funkce
x_grid = np.linspace(-0.5, 2, 100)
y_grid = np.linspace(-0.5, 3, 100)
X, Y = np.meshgrid(x_grid, y_grid)
Z = (X - 1)**2 + (Y - 2)**2
contour = ax.contour(X, Y, Z, levels=20, cmap='viridis')
ax.clabel(contour, inline=True, fontsize=8)
# Trajektorie
ax.plot(historie_x, historie_y, 'r.-', markersize=8, label='Gradient descent')
ax.plot(1, 2, 'g*', markersize=20, label='Optimum')
ax.plot(historie_x[0], historie_y[0], 'bo', markersize=12, label='Start')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Gradient Descent pro f(x,y) = (x-1)² + (y-2)²')
ax.legend()
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()Počátek: (0.0000, 0.0000)
Konec: (1.0000, 2.0000)
Optimum: (1.0000, 2.0000)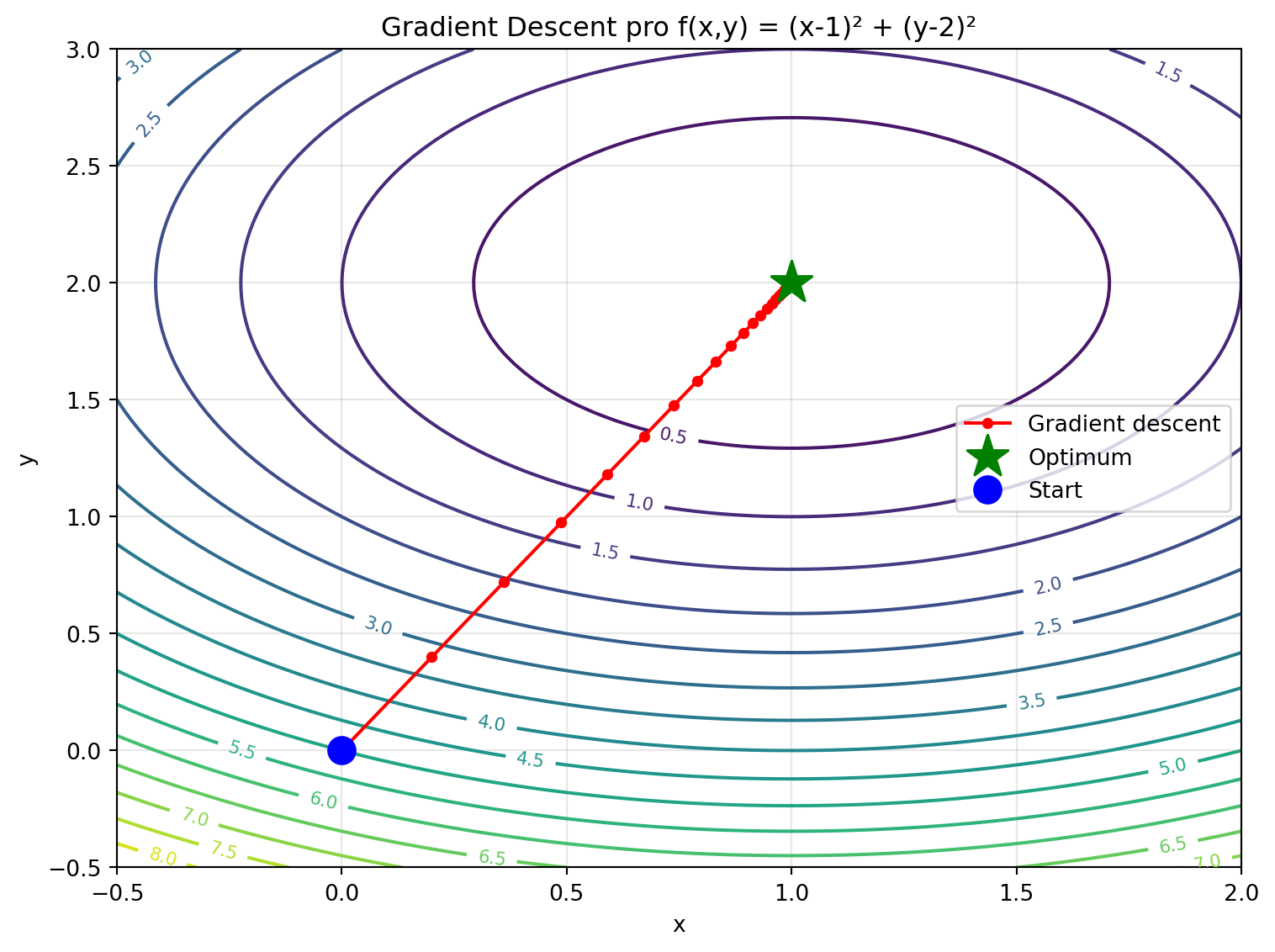
Zadání: Natrénujte lineární model \(y = wx + b\) na datech.
Řešení:
# Generujeme data: y = 2x + 1 + šum
import matplotlib.pyplot as plt
torch.manual_seed(42)
X = torch.linspace(0, 5, 20)
y_true = 2 * X + 1 + torch.randn(20) * 0.5
# Parametry modelu
w = torch.tensor(0.0, requires_grad=True)
b = torch.tensor(0.0, requires_grad=True)
learning_rate = 0.01
losses = []
for epoch in range(200):
# Forward pass
y_pred = w * X + b
# MSE loss
loss = ((y_pred - y_true)**2).mean()
losses.append(loss.item())
# Backward pass
loss.backward()
# Update parametrů
with torch.no_grad():
w -= learning_rate * w.grad
b -= learning_rate * b.grad
w.grad.zero_()
b.grad.zero_()
print(f"Naučené parametry:")
print(f"w = {w.item():.4f} (skutečné: 2.0)")
print(f"b = {b.item():.4f} (skutečné: 1.0)")
# Vizualizace
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
# Data a model
ax1.scatter(X, y_true, label='Data', alpha=0.7)
X_line = torch.linspace(0, 5, 100)
y_line = w.detach() * X_line + b.detach()
ax1.plot(X_line, y_line, 'r-', lw=2, label=f'Model: y = {w.item():.2f}x + {b.item():.2f}')
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.legend()
ax1.set_title('Lineární regrese s PyTorch')
ax1.grid(True, alpha=0.3)
# Loss
ax2.plot(losses)
ax2.set_xlabel('Epocha')
ax2.set_ylabel('Loss (MSE)')
ax2.set_title('Průběh tréninku')
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()Naučené parametry:
w = 1.9852 (skutečné: 2.0)
b = 1.0806 (skutečné: 1.0)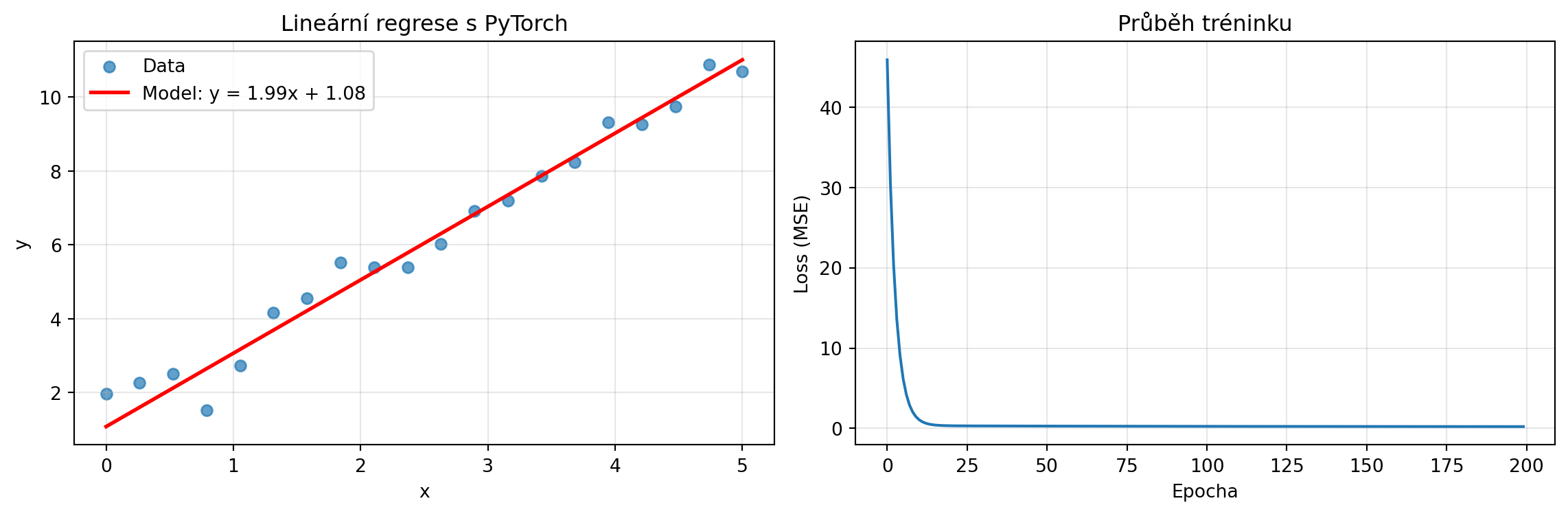
Pro hlubší pochopení si implementujeme zjednodušenou verzi autograd:
class Hodnota:
"""Třída pro automatické derivování."""
def __init__(self, data, potomci=(), operace=''):
self.data = data
self.grad = 0
self._backward = lambda: None
self._potomci = set(potomci)
self._operace = operace
def __repr__(self):
return f"Hodnota({self.data:.4f})"
def __add__(self, other):
other = other if isinstance(other, Hodnota) else Hodnota(other)
vysledek = Hodnota(self.data + other.data, (self, other), '+')
def _backward():
self.grad += vysledek.grad
other.grad += vysledek.grad
vysledek._backward = _backward
return vysledek
def __mul__(self, other):
other = other if isinstance(other, Hodnota) else Hodnota(other)
vysledek = Hodnota(self.data * other.data, (self, other), '*')
def _backward():
self.grad += other.data * vysledek.grad
other.grad += self.data * vysledek.grad
vysledek._backward = _backward
return vysledek
def __pow__(self, n):
vysledek = Hodnota(self.data ** n, (self,), f'^{n}')
def _backward():
self.grad += n * self.data**(n-1) * vysledek.grad
vysledek._backward = _backward
return vysledek
def backward(self):
"""Zpětný průchod pomocí topologického řazení."""
topo = []
navstivene = set()
def buduj_topo(v):
if v not in navstivene:
navstivene.add(v)
for potomek in v._potomci:
buduj_topo(potomek)
topo.append(v)
buduj_topo(self)
self.grad = 1
for v in reversed(topo):
v._backward()
# Test naší implementace
x = Hodnota(3)
y = Hodnota(2)
# f = (x + y) * (x - y) = x² - y²
f = (x + y) * (x + (y * -1))
print(f"f = {f}")
# Zpětný průchod
f.backward()
print(f"∂f/∂x = {x.grad}") # Mělo by být 2x = 6
print(f"∂f/∂y = {y.grad}") # Mělo by být -2y = -4f = Hodnota(5.0000)
∂f/∂x = 6
∂f/∂y = -4backward() a máme gradientyAutomatická derivace je základem moderního strojového učení. Bez ní by trénink neuronových sítí s miliony parametrů nebyl prakticky možný. V dalších kapitolách budeme automatickou derivaci používat pro optimalizaci a trénink skutečných modelů.