# Náhodné veličiny {#sec-nahodne-veliciny}
## Motivace: Od událostí k číslům
V minulé kapitole jsme pracovali s událostmi jako "padne šestka" nebo "e-mail je spam". Ale v praxi často potřebujeme pracovat s **číselnými hodnotami**:
- Kolik padne na kostce?
- Jaká je dnešní teplota?
- Kolik slov má vygenerovaná věta?
- Jaká je ztráta (loss) neuronové sítě?
**Náhodná veličina** je způsob, jak přiřadit číselné hodnoty výsledkům náhodných pokusů. Díky tomu můžeme počítat průměry, rozptyly a další statistiky.
## Co je náhodná veličina?
::: {.callout-note}
## Definice: Náhodná veličina
**Náhodná veličina** $X$ je funkce, která přiřazuje každému možnému výsledku náhodného pokusu reálné číslo.
:::
Rozlišujeme dva typy:
1. **Diskrétní náhodná veličina**: Nabývá konečně nebo spočetně mnoha hodnot (např. 1, 2, 3, 4, 5, 6 na kostce)
2. **Spojitá náhodná veličina**: Může nabývat libovolné hodnoty z nějakého intervalu (např. teplota, hmotnost)
```{python}
import numpy as np
import matplotlib.pyplot as plt
# Příklad: Náhodná veličina X = "číslo na kostce"
# X může nabývat hodnot 1, 2, 3, 4, 5, 6
hodnoty = [1, 2, 3, 4, 5, 6]
pravdepodobnosti = [1/6] * 6
print("Náhodná veličina X = 'číslo na kostce'")
print("-" * 35)
for x, p in zip(hodnoty, pravdepodobnosti):
print(f"P(X = {x}) = {p:.4f}")
print(f"\nSoučet pravděpodobností: {sum(pravdepodobnosti):.4f}")
```
## Rozdělení pravděpodobnosti
Rozdělení pravděpodobnosti popisuje, jaké hodnoty může náhodná veličina nabývat a s jakou pravděpodobností.
### Diskrétní rozdělení
Pro diskrétní veličinu definujeme **pravděpodobnostní funkci** $P(X = x)$:
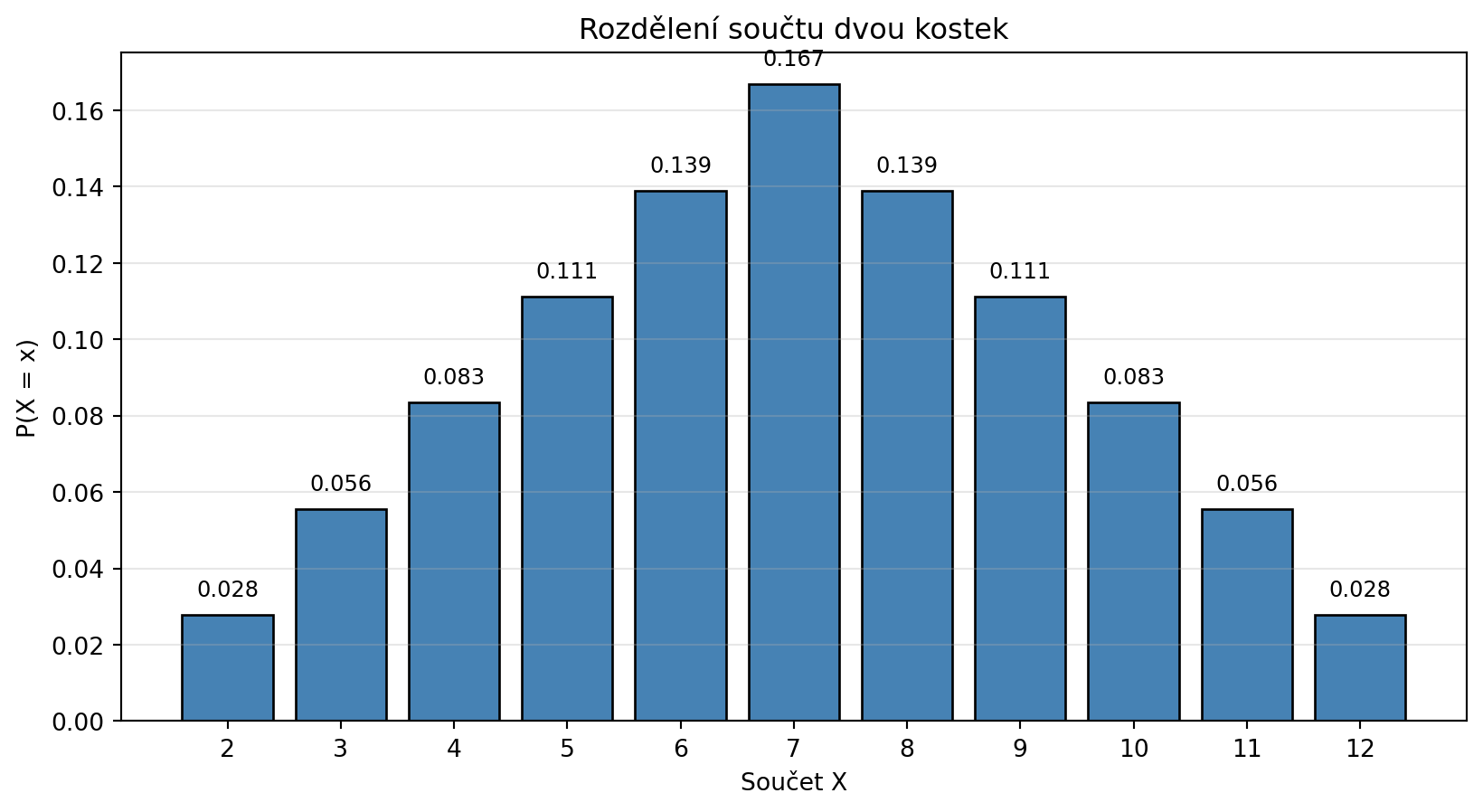
```{python}
# Příklad: Součet dvou kostek
# X = součet hodnot na dvou kostkách
import matplotlib.pyplot as plt
def soucet_kostek():
"""Vrátí rozdělení součtu dvou kostek."""
rozdeleni = {}
for k1 in range(1, 7):
for k2 in range(1, 7):
soucet = k1 + k2
rozdeleni[soucet] = rozdeleni.get(soucet, 0) + 1
# Převedeme na pravděpodobnosti
celkem = 36
for k in rozdeleni:
rozdeleni[k] /= celkem
return rozdeleni
rozdeleni = soucet_kostek()
plt.figure(figsize=(10, 5))
hodnoty = list(rozdeleni.keys())
probs = list(rozdeleni.values())
plt.bar(hodnoty, probs, color='steelblue', edgecolor='black')
plt.xlabel('Součet X')
plt.ylabel('P(X = x)')
plt.title('Rozdělení součtu dvou kostek')
plt.xticks(range(2, 13))
for x, p in zip(hodnoty, probs):
plt.text(x, p + 0.005, f'{p:.3f}', ha='center', fontsize=9)
plt.grid(axis='y', alpha=0.3)
plt.show()
print("Nejpravděpodobnější součet je 7")
print(f"P(X = 7) = {rozdeleni[7]:.4f} = 6/36")
```
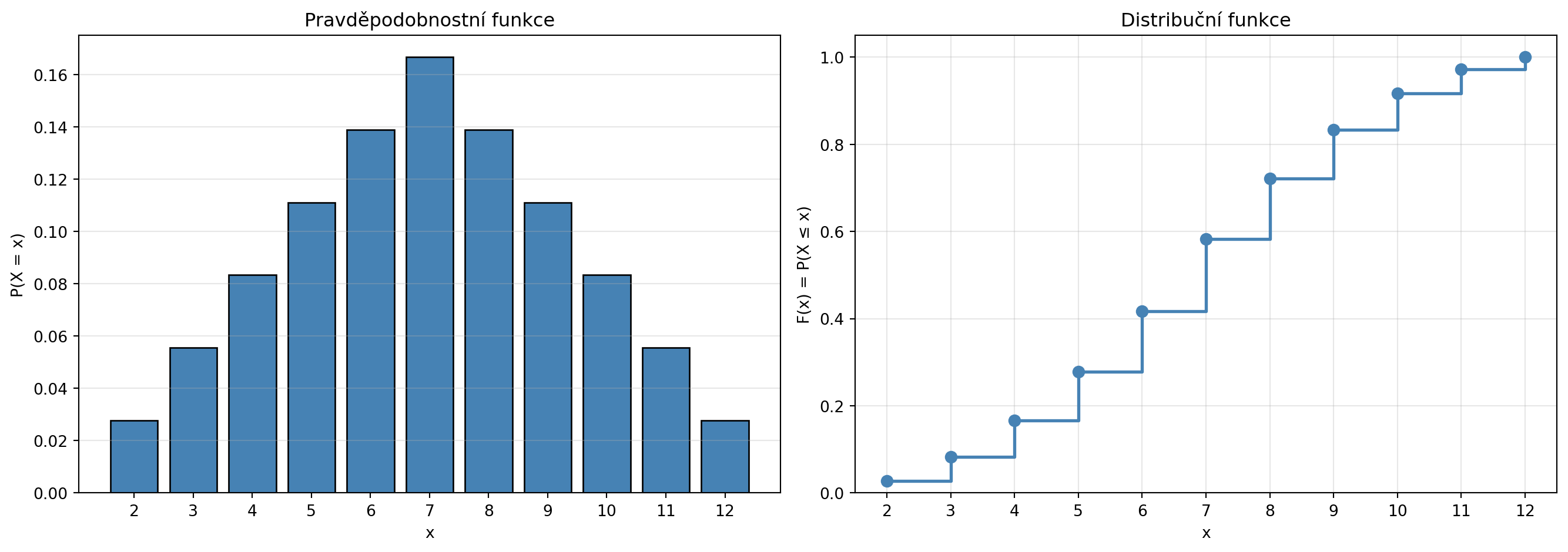
### Distribuční funkce
**Distribuční funkce** $F(x) = P(X \leq x)$ udává pravděpodobnost, že náhodná veličina nabude hodnoty menší nebo rovné $x$:
```{python}
# Distribuční funkce pro součet kostek
import matplotlib.pyplot as plt
def distribucni_funkce(rozdeleni):
F = {}
kumulativni = 0
for x in sorted(rozdeleni.keys()):
kumulativni += rozdeleni[x]
F[x] = kumulativni
return F
F = distribucni_funkce(rozdeleni)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))
# Pravděpodobnostní funkce
ax1.bar(hodnoty, probs, color='steelblue', edgecolor='black')
ax1.set_xlabel('x')
ax1.set_ylabel('P(X = x)')
ax1.set_title('Pravděpodobnostní funkce')
ax1.set_xticks(range(2, 13))
ax1.grid(axis='y', alpha=0.3)
# Distribuční funkce
x_vals = list(F.keys())
F_vals = list(F.values())
ax2.step(x_vals, F_vals, where='post', color='steelblue', lw=2)
ax2.scatter(x_vals, F_vals, color='steelblue', s=50, zorder=5)
ax2.set_xlabel('x')
ax2.set_ylabel('F(x) = P(X ≤ x)')
ax2.set_title('Distribuční funkce')
ax2.set_xticks(range(2, 13))
ax2.set_ylim(0, 1.05)
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("Příklad použití distribuční funkce:")
print(f"P(X ≤ 7) = F(7) = {F[7]:.4f}")
print(f"P(X > 7) = 1 - F(7) = {1 - F[7]:.4f}")
```
## Střední hodnota (Očekávaná hodnota)
Střední hodnota je "průměrná" hodnota náhodné veličiny, vážená pravděpodobnostmi:
::: {.callout-note}
## Definice: Střední hodnota
Pro diskrétní náhodnou veličinu $X$:
$$E[X] = \sum_x x \cdot P(X = x)$$
Střední hodnotu značíme také $\mu$ nebo $\langle X \rangle$.
:::
```{python}
# Střední hodnota kostky
def stredni_hodnota(hodnoty, pravdepodobnosti):
return sum(x * p for x, p in zip(hodnoty, pravdepodobnosti))
# Jedna kostka
kostka_hodnoty = [1, 2, 3, 4, 5, 6]
kostka_probs = [1/6] * 6
E_kostka = stredni_hodnota(kostka_hodnoty, kostka_probs)
print(f"E[jedna kostka] = {E_kostka:.4f}")
# Součet dvou kostek
E_soucet = stredni_hodnota(list(rozdeleni.keys()), list(rozdeleni.values()))
print(f"E[součet kostek] = {E_soucet:.4f}")
print(f"\nOvěření: E[X+Y] = E[X] + E[Y] = 3.5 + 3.5 = {3.5 + 3.5}")
```
### Vlastnosti střední hodnoty
```{python}
# E[aX + b] = a*E[X] + b
import numpy as np
a, b = 2, 3
E_X = 3.5 # střední hodnota kostky
E_aX_b = a * E_X + b
print(f"Pro X = kostka, a = {a}, b = {b}:")
print(f"E[{a}X + {b}] = {a} * E[X] + {b} = {a} * {E_X} + {b} = {E_aX_b}")
# Simulace pro ověření
np.random.seed(42)
kostky = np.random.randint(1, 7, size=100000)
transformovane = a * kostky + b
print(f"\nSimulace (100000 hodů):")
print(f"Průměr 2X + 3 = {np.mean(transformovane):.4f}")
```
## Rozptyl a směrodatná odchylka
Rozptyl měří, jak moc jsou hodnoty "rozptýlené" kolem střední hodnoty:
::: {.callout-note}
## Definice: Rozptyl
$$\text{Var}(X) = E[(X - \mu)^2] = E[X^2] - (E[X])^2$$
Značíme také $\sigma^2$.
**Směrodatná odchylka** je odmocnina z rozptylu:
$$\sigma = \sqrt{\text{Var}(X)}$$
:::
```{python}
import numpy as np
def rozptyl(hodnoty, pravdepodobnosti):
mu = stredni_hodnota(hodnoty, pravdepodobnosti)
return sum((x - mu)**2 * p for x, p in zip(hodnoty, pravdepodobnosti))
# Rozptyl kostky
var_kostka = rozptyl(kostka_hodnoty, kostka_probs)
std_kostka = np.sqrt(var_kostka)
print(f"Rozptyl kostky: Var(X) = {var_kostka:.4f}")
print(f"Směrodatná odchylka: σ = {std_kostka:.4f}")
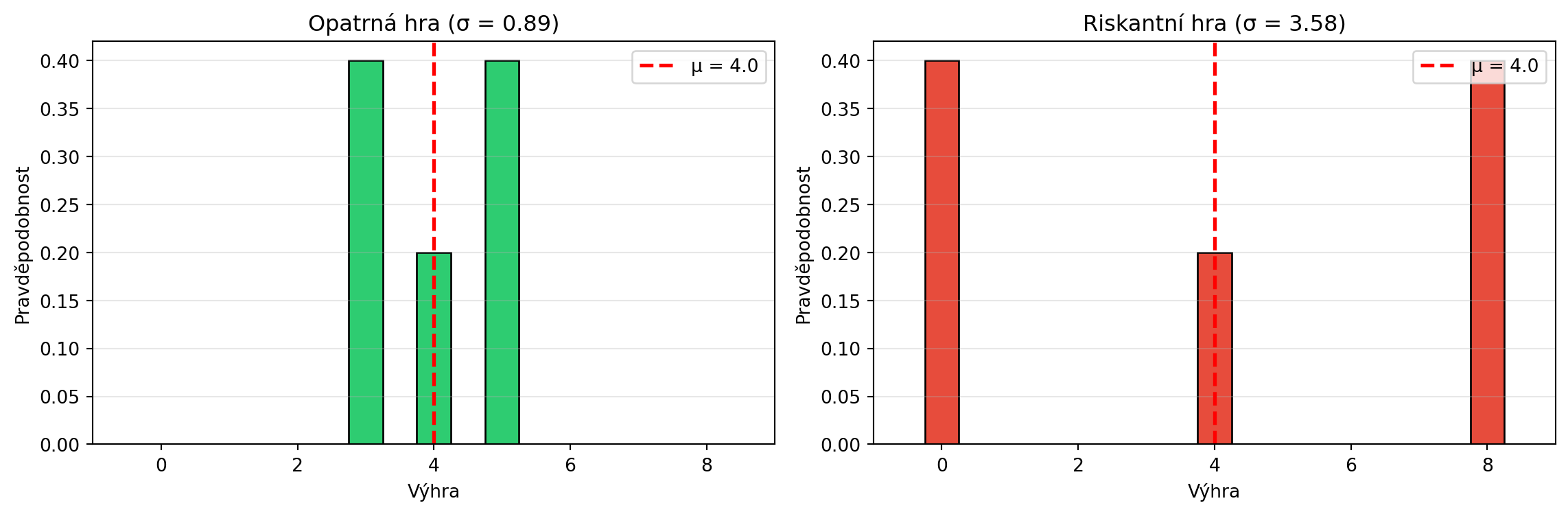
# Porovnání dvou různých rozdělení
# "Opatrná" vs "riskantní" hra
opatrna = {3: 0.4, 4: 0.2, 5: 0.4} # Střední hodnota ~4
riskantni = {0: 0.4, 4: 0.2, 8: 0.4} # Střední hodnota ~4
mu_o = sum(x*p for x, p in opatrna.items())
mu_r = sum(x*p for x, p in riskantni.items())
var_o = sum((x-mu_o)**2*p for x, p in opatrna.items())
var_r = sum((x-mu_r)**2*p for x, p in riskantni.items())
print(f"\nPorovnání dvou her:")
print(f"Opatrná: E[X] = {mu_o:.1f}, Var(X) = {var_o:.2f}, σ = {np.sqrt(var_o):.2f}")
print(f"Riskantní: E[X] = {mu_r:.1f}, Var(X) = {var_r:.2f}, σ = {np.sqrt(var_r):.2f}")
print(f"\nStejná střední hodnota, ale riskantní hra má větší rozptyl!")
```
### Vizualizace rozptylu
```{python}
import numpy as np
import matplotlib.pyplot as plt
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
# Opatrná hra
ax1.bar(list(opatrna.keys()), list(opatrna.values()), color='#2ecc71', edgecolor='black', width=0.5)
ax1.axvline(x=mu_o, color='red', linestyle='--', lw=2, label=f'μ = {mu_o:.1f}')
ax1.set_xlabel('Výhra')
ax1.set_ylabel('Pravděpodobnost')
ax1.set_title(f'Opatrná hra (σ = {np.sqrt(var_o):.2f})')
ax1.legend()
ax1.set_xlim(-1, 9)
ax1.grid(axis='y', alpha=0.3)
# Riskantní hra
ax2.bar(list(riskantni.keys()), list(riskantni.values()), color='#e74c3c', edgecolor='black', width=0.5)
ax2.axvline(x=mu_r, color='red', linestyle='--', lw=2, label=f'μ = {mu_r:.1f}')
ax2.set_xlabel('Výhra')
ax2.set_ylabel('Pravděpodobnost')
ax2.set_title(f'Riskantní hra (σ = {np.sqrt(var_r):.2f})')
ax2.legend()
ax2.set_xlim(-1, 9)
ax2.grid(axis='y', alpha=0.3)
plt.tight_layout()
plt.show()
```
## Důležitá diskrétní rozdělení
### Bernoulliho rozdělení
Popisuje jeden pokus s dvěma možnými výsledky (úspěch/neúspěch):
```{python}
# Bernoulliho rozdělení
# X = 1 s pravděpodobností p
# X = 0 s pravděpodobností 1-p
import numpy as np
p = 0.7 # Pravděpodobnost úspěchu
E_bernoulli = p
Var_bernoulli = p * (1 - p)
print(f"Bernoulliho rozdělení s p = {p}:")
print(f"E[X] = p = {E_bernoulli}")
print(f"Var(X) = p(1-p) = {Var_bernoulli}")
# Simulace
np.random.seed(42)
vzorky = np.random.binomial(1, p, size=10000)
print(f"\nSimulace 10000 pokusů:")
print(f"Průměr = {np.mean(vzorky):.4f}")
print(f"Rozptyl = {np.var(vzorky):.4f}")
```
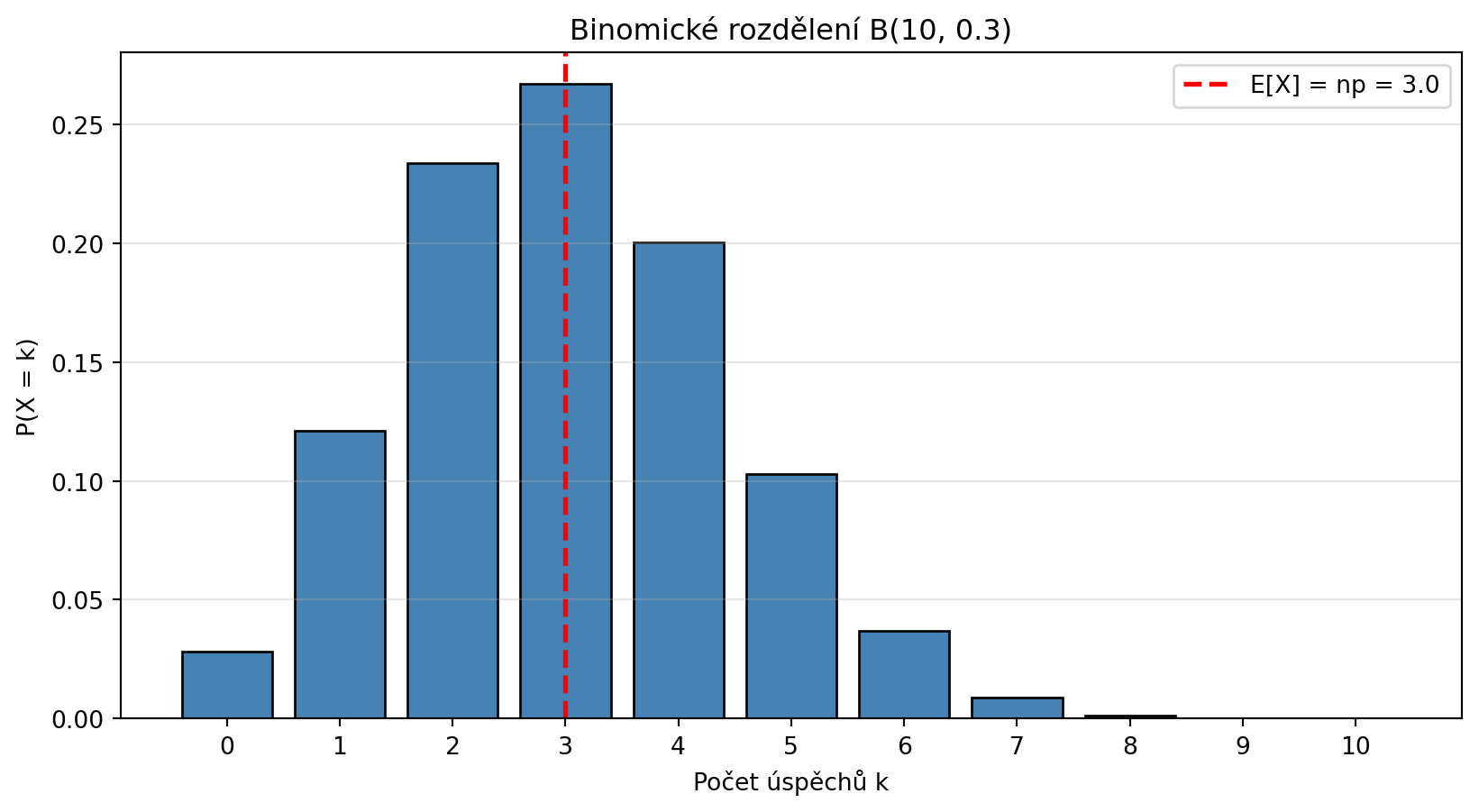
### Binomické rozdělení
Počet úspěchů v $n$ nezávislých Bernoulliho pokusech:
::: {.callout-note}
## Binomické rozdělení
$$P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}$$
kde $\binom{n}{k} = \frac{n!}{k!(n-k)!}$ je kombinační číslo.
- $E[X] = np$
- $\text{Var}(X) = np(1-p)$
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
from math import comb
n = 10 # počet pokusů
p = 0.3 # pravděpodobnost úspěchu
def binom_pmf(k, n, p):
"""Pravděpodobnostní funkce binomického rozdělení."""
return comb(n, k) * (p ** k) * ((1-p) ** (n-k))
k_values = np.arange(0, n+1)
probs = [binom_pmf(k, n, p) for k in k_values]
plt.figure(figsize=(10, 5))
plt.bar(k_values, probs, color='steelblue', edgecolor='black')
plt.xlabel('Počet úspěchů k')
plt.ylabel('P(X = k)')
plt.title(f'Binomické rozdělení B({n}, {p})')
plt.xticks(k_values)
# Vyznačení střední hodnoty
mu = n * p
plt.axvline(x=mu, color='red', linestyle='--', lw=2, label=f'E[X] = np = {mu}')
plt.legend()
plt.grid(axis='y', alpha=0.3)
plt.show()
print(f"E[X] = np = {n}×{p} = {mu}")
print(f"Var(X) = np(1-p) = {n*p*(1-p)}")
```
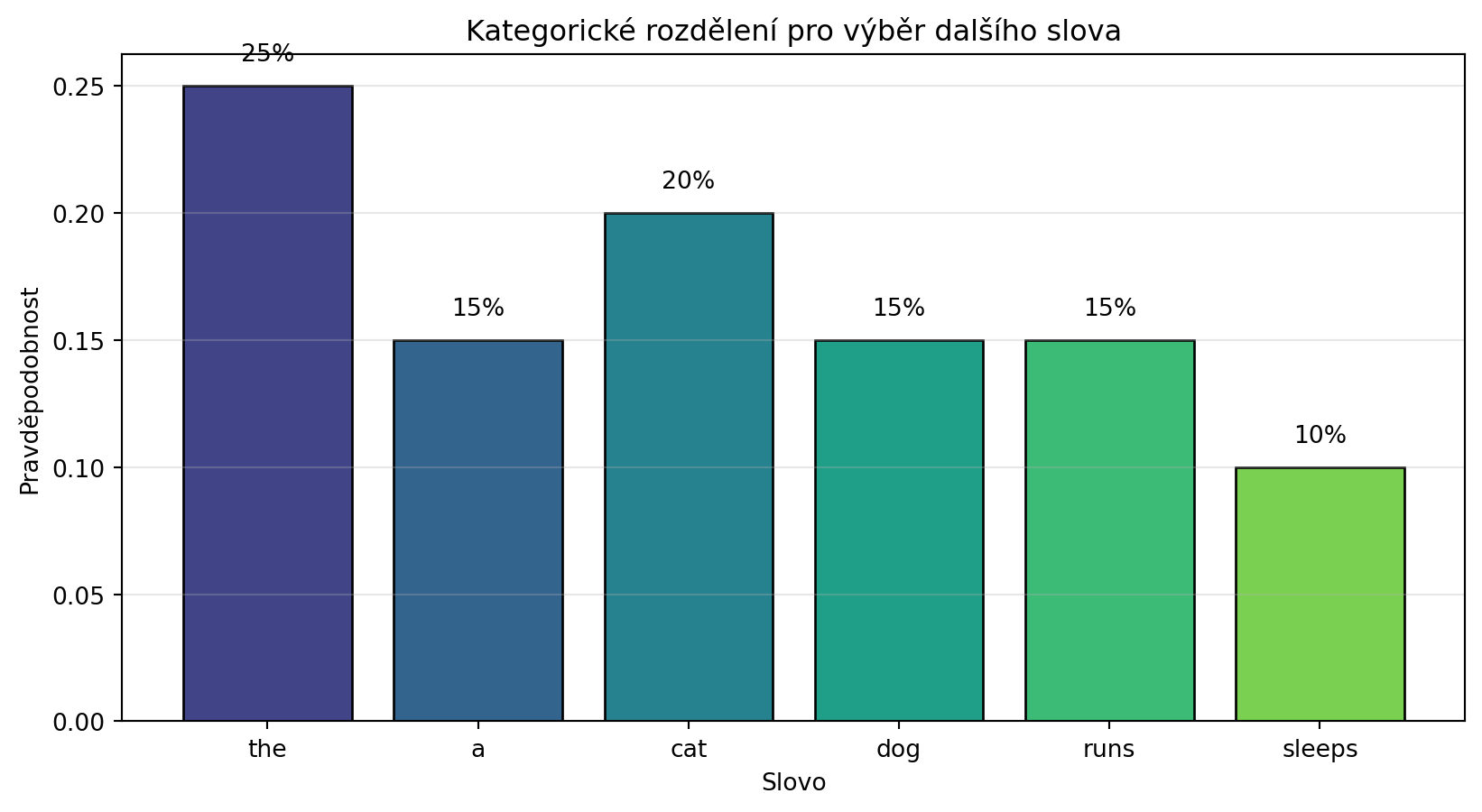
### Kategorické rozdělení (Multinomial)
Zobecnění Bernoulliho rozdělení na více než dva výsledky - přesně to, co potřebujeme pro **jazykové modely**:
```{python}
# Kategorické rozdělení pro výběr slova
import numpy as np
import matplotlib.pyplot as plt
slovnik = ['the', 'a', 'cat', 'dog', 'runs', 'sleeps']
pravdepodobnosti_slov = [0.25, 0.15, 0.2, 0.15, 0.15, 0.1]
print("Kategorické rozdělení pro jazykový model:")
print("-" * 40)
for slovo, p in zip(slovnik, pravdepodobnosti_slov):
print(f"P('{slovo}') = {p:.2f}")
# Vzorkování - takto jazykový model generuje slova
np.random.seed(42)
vygenerovana_slova = np.random.choice(slovnik, size=10, p=pravdepodobnosti_slov)
print(f"\nVygenerovaná slova: {list(vygenerovana_slova)}")
# Vizualizace
plt.figure(figsize=(10, 5))
colors = plt.cm.viridis(np.linspace(0.2, 0.8, len(slovnik)))
bars = plt.bar(slovnik, pravdepodobnosti_slov, color=colors, edgecolor='black')
plt.xlabel('Slovo')
plt.ylabel('Pravděpodobnost')
plt.title('Kategorické rozdělení pro výběr dalšího slova')
for bar, p in zip(bars, pravdepodobnosti_slov):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.01,
f'{p:.0%}', ha='center')
plt.grid(axis='y', alpha=0.3)
plt.show()
```
## Spojité náhodné veličiny
Pro spojité veličiny používáme **hustotu pravděpodobnosti** $f(x)$:
$$P(a \leq X \leq b) = \int_a^b f(x)\, dx$$
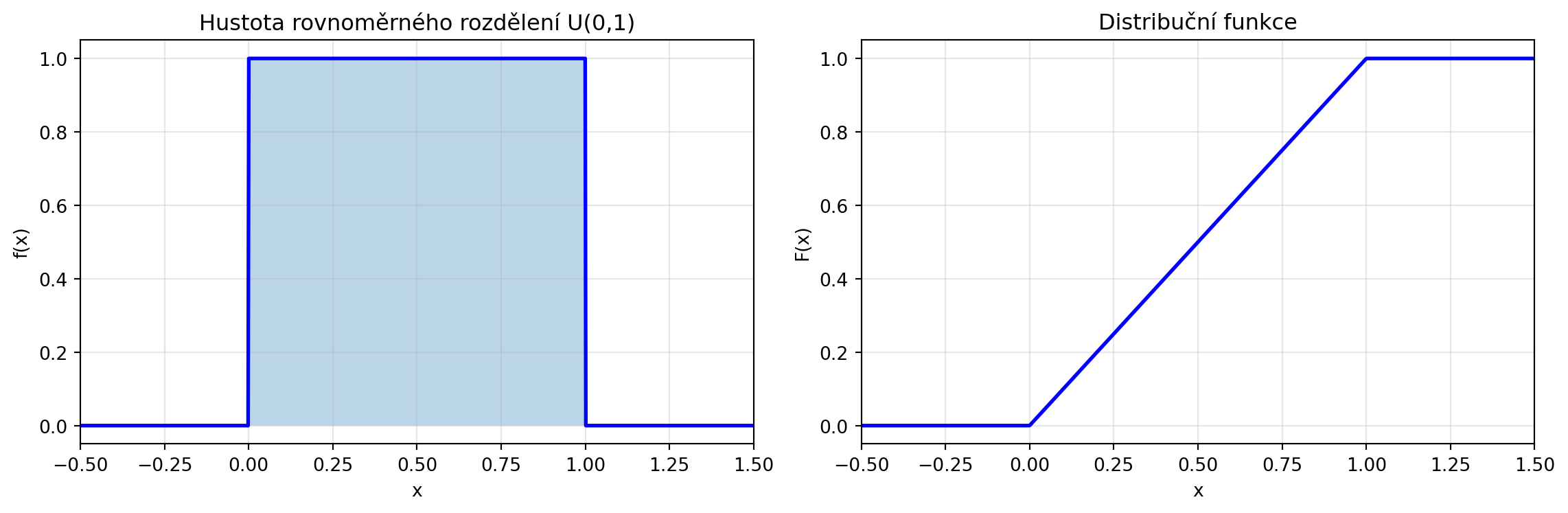
### Rovnoměrné rozdělení
Všechny hodnoty v intervalu jsou stejně pravděpodobné:
```{python}
# Rovnoměrné rozdělení na [0, 1]
import numpy as np
import matplotlib.pyplot as plt
def uniform_pdf(x, a=0, b=1):
"""Hustota rovnoměrného rozdělení."""
return np.where((x >= a) & (x <= b), 1/(b-a), 0)
def uniform_cdf(x, a=0, b=1):
"""Distribuční funkce rovnoměrného rozdělení."""
return np.clip((x - a) / (b - a), 0, 1)
x = np.linspace(-0.5, 1.5, 1000)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
# Hustota
ax1.plot(x, uniform_pdf(x), 'b-', lw=2)
ax1.fill_between(x, uniform_pdf(x), alpha=0.3)
ax1.set_xlabel('x')
ax1.set_ylabel('f(x)')
ax1.set_title('Hustota rovnoměrného rozdělení U(0,1)')
ax1.set_xlim(-0.5, 1.5)
ax1.grid(True, alpha=0.3)
# Distribuční funkce
ax2.plot(x, uniform_cdf(x), 'b-', lw=2)
ax2.set_xlabel('x')
ax2.set_ylabel('F(x)')
ax2.set_title('Distribuční funkce')
ax2.set_xlim(-0.5, 1.5)
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# E[X] = (a+b)/2 = 0.5, Var(X) = (b-a)^2/12 = 1/12
print(f"E[X] = 0.5")
print(f"Var(X) = {1/12:.4f}")
```
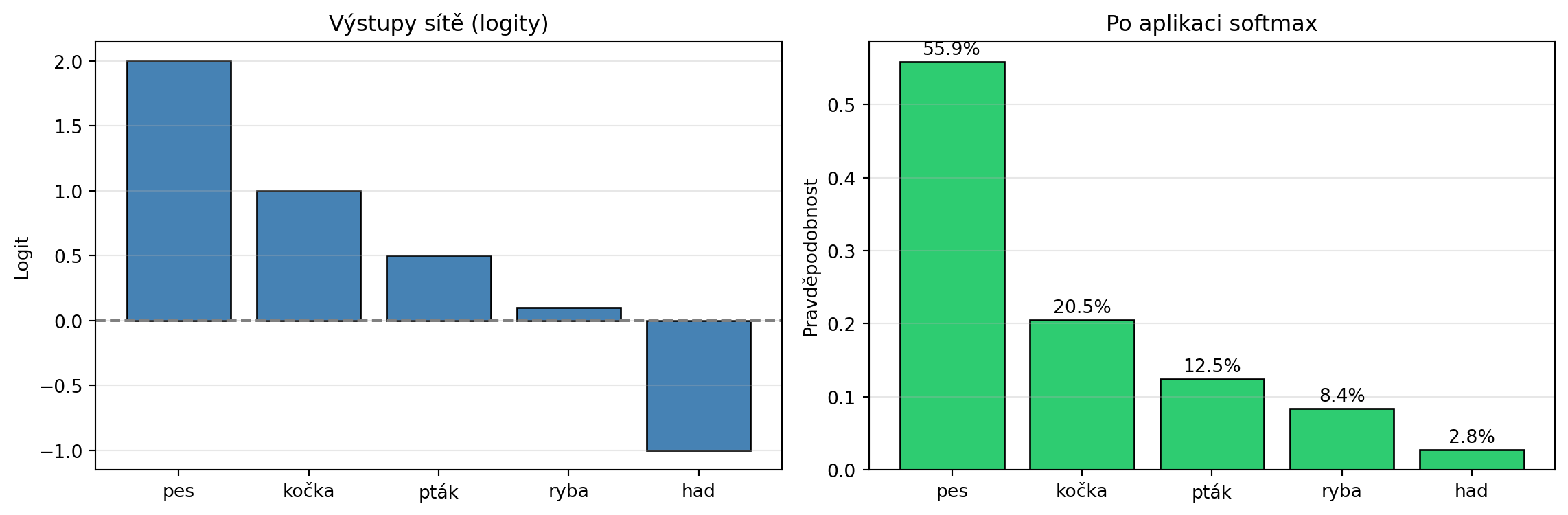
## Aplikace: Softmax a kategorické rozdělení
V neuronových sítích používáme **softmax** funkci k převodu libovolných čísel na pravděpodobnosti:
::: {.callout-note}
## Softmax funkce
Pro vektor $\mathbf{z} = (z_1, z_2, \ldots, z_K)$:
$$\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}}$$
Výstupem je vektor pravděpodobností - kategorické rozdělení.
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
def softmax(z):
"""Softmax funkce."""
exp_z = np.exp(z - np.max(z)) # numerická stabilita
return exp_z / np.sum(exp_z)
# Příklad: Výstupy neuronové sítě pro 5 slov
logits = np.array([2.0, 1.0, 0.5, 0.1, -1.0])
slova = ['pes', 'kočka', 'pták', 'ryba', 'had']
probs = softmax(logits)
print("Převod logitů na pravděpodobnosti pomocí softmax:")
print("-" * 50)
print(f"{'Slovo':<10} {'Logit':<10} {'Pravděpodobnost':<15}")
print("-" * 50)
for slovo, logit, prob in zip(slova, logits, probs):
print(f"{slovo:<10} {logit:<10.2f} {prob:<15.4f}")
print("-" * 50)
print(f"{'Součet':<10} {'':<10} {sum(probs):<15.4f}")
# Vizualizace
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.bar(slova, logits, color='steelblue', edgecolor='black')
ax1.set_ylabel('Logit')
ax1.set_title('Výstupy sítě (logity)')
ax1.axhline(y=0, color='gray', linestyle='--')
ax1.grid(axis='y', alpha=0.3)
ax2.bar(slova, probs, color='#2ecc71', edgecolor='black')
ax2.set_ylabel('Pravděpodobnost')
ax2.set_title('Po aplikaci softmax')
for i, p in enumerate(probs):
ax2.text(i, p + 0.01, f'{p:.1%}', ha='center')
ax2.grid(axis='y', alpha=0.3)
plt.tight_layout()
plt.show()
```
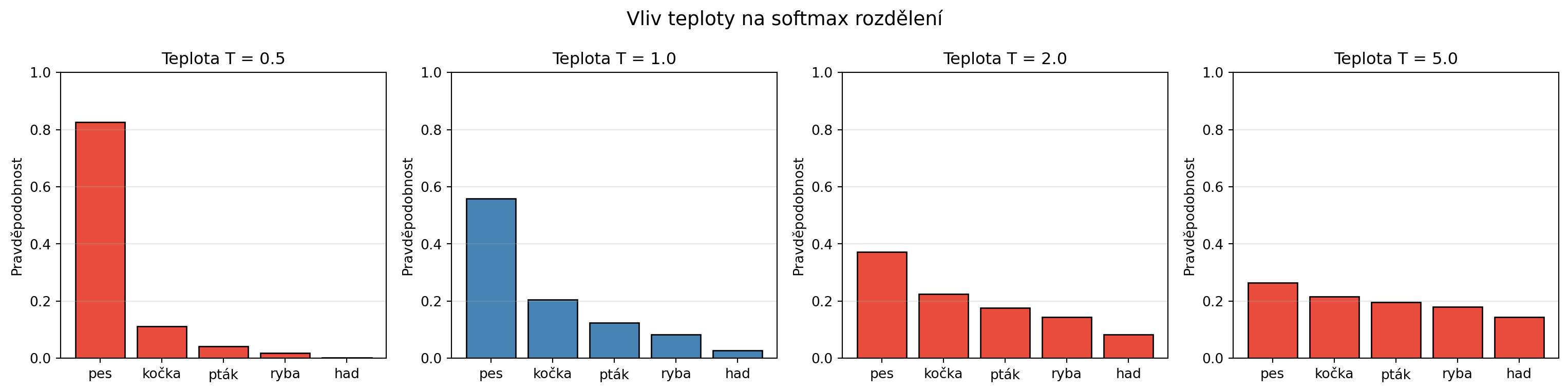
### Teplota v softmax
Parametr **teplota** ($T$) kontroluje "ostrost" rozdělení:
```{python}
import numpy as np
import matplotlib.pyplot as plt
def softmax_s_teplotou(z, T=1.0):
"""Softmax s teplotou."""
exp_z = np.exp((z - np.max(z)) / T)
return exp_z / np.sum(exp_z)
logits = np.array([2.0, 1.0, 0.5, 0.1, -1.0])
teploty = [0.5, 1.0, 2.0, 5.0]
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
for ax, T in zip(axes, teploty):
probs = softmax_s_teplotou(logits, T)
ax.bar(slova, probs, color='steelblue' if T == 1 else '#e74c3c', edgecolor='black')
ax.set_title(f'Teplota T = {T}')
ax.set_ylabel('Pravděpodobnost')
ax.set_ylim(0, 1)
ax.grid(axis='y', alpha=0.3)
plt.suptitle('Vliv teploty na softmax rozdělení', fontsize=14)
plt.tight_layout()
plt.show()
print("Nízká teplota → ostřejší rozdělení (model je jistější)")
print("Vysoká teplota → plošší rozdělení (model je méně jistý)")
```
## Řešené příklady
### Příklad 1: Střední hodnota a rozptyl
**Zadání**: Hrajete hru, kde s pravděpodobností 0.3 vyhrajete 10 Kč a s pravděpodobností 0.7 prohrajete 3 Kč. Jaká je střední hodnota zisku?
**Řešení**:
```{python}
import numpy as np
vyhra = 10
prohra = -3
p_vyhra = 0.3
p_prohra = 0.7
E_zisk = vyhra * p_vyhra + prohra * p_prohra
Var_zisk = (vyhra - E_zisk)**2 * p_vyhra + (prohra - E_zisk)**2 * p_prohra
print(f"E[zisk] = {vyhra}×{p_vyhra} + ({prohra})×{p_prohra}")
print(f" = {vyhra * p_vyhra} + {prohra * p_prohra}")
print(f" = {E_zisk} Kč")
print(f"\nVar(zisk) = {Var_zisk:.2f}")
print(f"σ = {np.sqrt(Var_zisk):.2f} Kč")
if E_zisk > 0:
print(f"\nHra je v průměru výhodná!")
else:
print(f"\nHra je v průměru nevýhodná!")
```
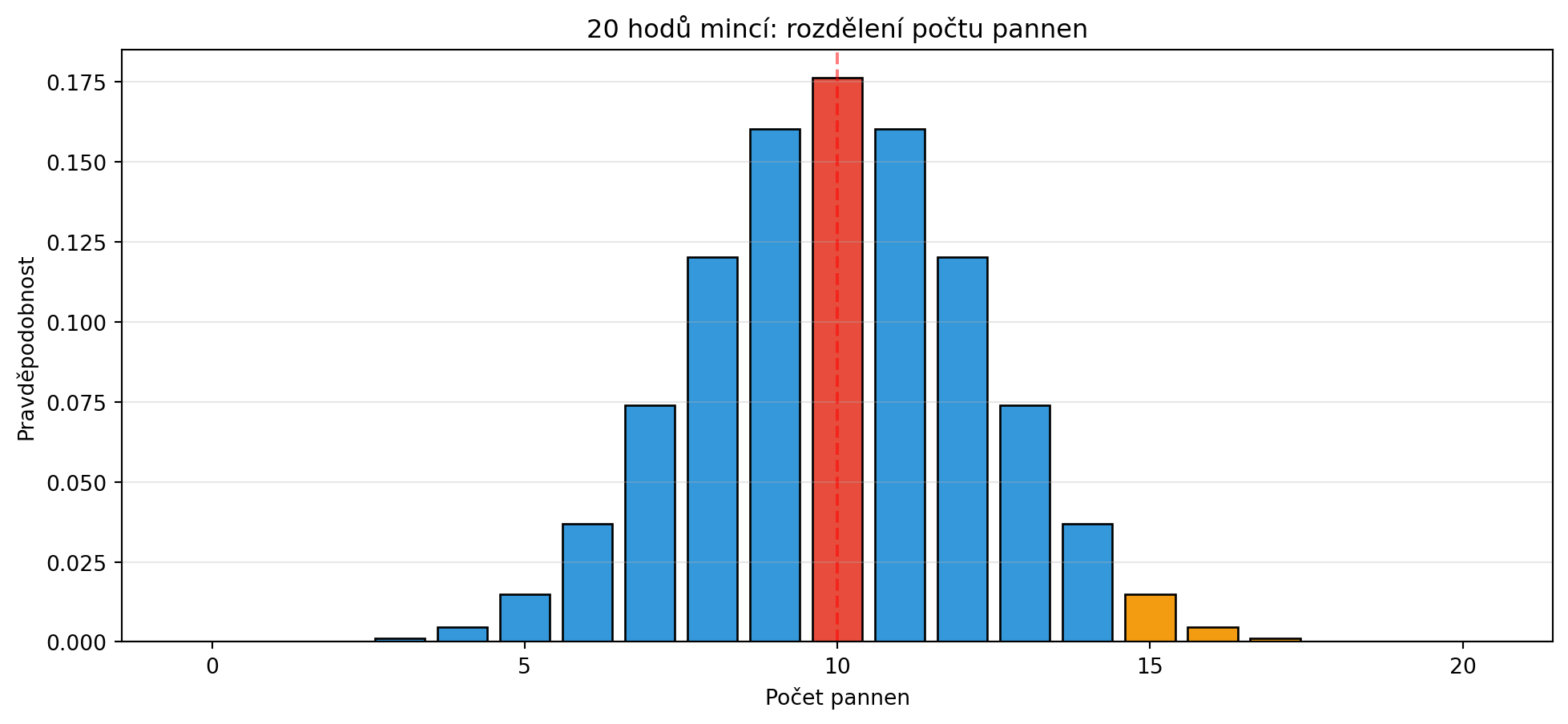
### Příklad 2: Binomické rozdělení
**Zadání**: Házíte mincí 20×. Jaká je pravděpodobnost, že padne přesně 10 pannen? A jaká je pravděpodobnost, že padne alespoň 15 pannen?
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
from math import comb
n = 20
p = 0.5
def binom_pmf(k, n, p):
"""Pravděpodobnostní funkce binomického rozdělení."""
return comb(n, k) * (p ** k) * ((1-p) ** (n-k))
def binom_cdf(x, n, p):
"""Distribuční funkce binomického rozdělení."""
return sum(binom_pmf(k, n, p) for k in range(int(x) + 1))
# Přesně 10 pannen
P_presne_10 = binom_pmf(10, n, p)
print(f"P(X = 10) = {P_presne_10:.4f}")
# Alespoň 15 pannen
P_alespon_15 = 1 - binom_cdf(14, n, p) # = P(X >= 15) = 1 - P(X <= 14)
print(f"P(X ≥ 15) = {P_alespon_15:.4f}")
# Vizualizace
k = np.arange(0, n+1)
probs = [binom_pmf(ki, n, p) for ki in k]
plt.figure(figsize=(12, 5))
colors = ['#e74c3c' if i == 10 else '#f39c12' if i >= 15 else '#3498db' for i in k]
plt.bar(k, probs, color=colors, edgecolor='black')
plt.xlabel('Počet pannen')
plt.ylabel('Pravděpodobnost')
plt.title('20 hodů mincí: rozdělení počtu pannen')
plt.axvline(x=10, color='red', linestyle='--', alpha=0.5)
plt.grid(axis='y', alpha=0.3)
plt.show()
```
### Příklad 3: Jazykový model - generování textu
**Zadání**: Implementujte jednoduché generování textu pomocí kategorického vzorkování.
**Řešení**:
```{python}
import numpy as np
np.random.seed(42)
# Jednoduchý bigramový model
model = {
'<start>': {'Dnes': 0.3, 'Včera': 0.2, 'Zítra': 0.2, 'Já': 0.15, 'On': 0.15},
'Dnes': {'je': 0.5, 'bude': 0.3, 'jsem': 0.2},
'Včera': {'bylo': 0.6, 'jsem': 0.4},
'Zítra': {'bude': 0.7, 'budu': 0.3},
'Já': {'jsem': 0.5, 'budu': 0.3, 'mám': 0.2},
'On': {'je': 0.4, 'byl': 0.3, 'bude': 0.3},
'je': {'krásně': 0.3, 'hezky': 0.25, 'doma': 0.25, '<end>': 0.2},
'bude': {'pršet': 0.3, 'hezky': 0.3, 'dobře': 0.2, '<end>': 0.2},
'bylo': {'hezky': 0.4, 'špatně': 0.3, '<end>': 0.3},
'jsem': {'šťastný': 0.3, 'doma': 0.3, 'unavený': 0.2, '<end>': 0.2},
'budu': {'pracovat': 0.4, 'odpočívat': 0.3, '<end>': 0.3},
'mám': {'hlad': 0.4, 'radost': 0.3, '<end>': 0.3},
'byl': {'doma': 0.4, 'v_práci': 0.3, '<end>': 0.3},
}
def generuj_vetu(model, max_delka=10):
"""Generuje větu vzorkováním z modelu."""
veta = []
aktualni = '<start>'
for _ in range(max_delka):
if aktualni not in model:
break
distribuce = model[aktualni]
slova = list(distribuce.keys())
probs = list(distribuce.values())
dalsi = np.random.choice(slova, p=probs)
if dalsi == '<end>':
break
veta.append(dalsi)
aktualni = dalsi
return ' '.join(veta)
print("Vygenerované věty:")
print("-" * 40)
for i in range(5):
veta = generuj_vetu(model)
print(f"{i+1}. {veta}")
```
### Příklad 4: Porovnání různých softmax teplot
**Zadání**: Ukažte, jak teplota ovlivňuje výběr slov při generování.
**Řešení**:
```{python}
import numpy as np
logits = np.array([3.0, 2.0, 1.5, 0.5, -0.5])
slova = ['pes', 'kočka', 'pták', 'ryba', 'had']
print("Počet výběrů každého slova (z 1000 vzorků):")
print("-" * 55)
print(f"{'Slovo':<10}", end='')
for T in [0.3, 1.0, 3.0]:
print(f"{'T='+str(T):<12}", end='')
print()
print("-" * 55)
np.random.seed(42)
for slovo in slova:
print(f"{slovo:<10}", end='')
for T in [0.3, 1.0, 3.0]:
probs = softmax_s_teplotou(logits, T)
vyber = np.random.choice(slova, size=1000, p=probs)
pocet = np.sum(vyber == slovo)
print(f"{pocet:<12}", end='')
print()
print("-" * 55)
print("\nNízká T → častěji se vybírá nejpravděpodobnější slovo")
print("Vysoká T → výběr je více náhodný (více diversity)")
```
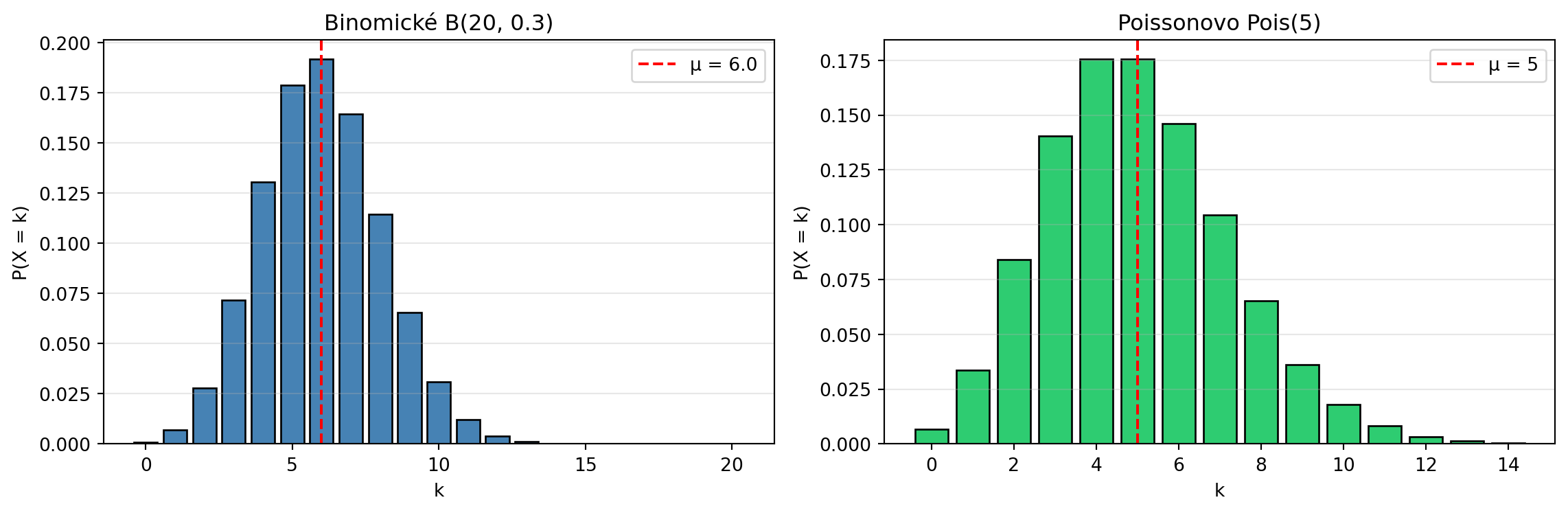
### Příklad 5: NumPy pro práci s rozděleními
**Zadání**: Ukažte, jak NumPy a SciPy pracují s náhodnými veličinami.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
from math import comb, factorial, exp
np.random.seed(42)
def binom_pmf(k, n, p):
"""Pravděpodobnostní funkce binomického rozdělení."""
return comb(n, k) * (p ** k) * ((1-p) ** (n-k))
def poisson_pmf(k, lam):
"""Pravděpodobnostní funkce Poissonova rozdělení."""
return (lam ** k) * exp(-lam) / factorial(k)
# Binomické rozdělení
n, p = 20, 0.3
mu_binom = n * p
var_binom = n * p * (1 - p)
print("Binomické rozdělení B(20, 0.3):")
print(f" Střední hodnota: {mu_binom}")
print(f" Rozptyl: {var_binom}")
# Vzorkování
vzorky = np.random.binomial(n, p, size=10)
print(f" 10 vzorků: {vzorky}")
# Poissonovo rozdělení (počet událostí za čas)
lam = 5
print(f"\nPoissonovo rozdělení Pois({lam}):")
print(f" Střední hodnota: {lam}")
print(f" Rozptyl: {lam}")
# Vizualizace
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
k_binom = np.arange(0, n+1)
probs_binom = [binom_pmf(k, n, p) for k in k_binom]
ax1.bar(k_binom, probs_binom, color='steelblue', edgecolor='black')
ax1.axvline(x=mu_binom, color='red', linestyle='--', label=f'μ = {mu_binom}')
ax1.set_xlabel('k')
ax1.set_ylabel('P(X = k)')
ax1.set_title(f'Binomické B({n}, {p})')
ax1.legend()
ax1.grid(axis='y', alpha=0.3)
k_pois = np.arange(0, 15)
probs_pois = [poisson_pmf(k, lam) for k in k_pois]
ax2.bar(k_pois, probs_pois, color='#2ecc71', edgecolor='black')
ax2.axvline(x=lam, color='red', linestyle='--', label=f'μ = {lam}')
ax2.set_xlabel('k')
ax2.set_ylabel('P(X = k)')
ax2.set_title(f'Poissonovo Pois({lam})')
ax2.legend()
ax2.grid(axis='y', alpha=0.3)
plt.tight_layout()
plt.show()
```
## Cvičení
::: {.callout-note icon=false}
## Cvičení 1: Kostky
Háčíte dvěma kostkami. Definujte náhodnou veličinu $X$ jako absolutní hodnotu rozdílu obou kostek. Najděte:
a) Rozdělení pravděpodobnosti
b) Střední hodnotu $E[X]$
c) Rozptyl $\text{Var}(X)$
:::
::: {.callout-note icon=false}
## Cvičení 2: Spravedlivá hra
Navrhněte hru, kde hází jedna kostka, taková, že střední hodnota výhry je 0 (férová hra). Kolik byste měli platit za vstup, pokud za každé hozené číslo dostanete tolik korun?
:::
::: {.callout-note icon=false}
## Cvičení 3: Binomické rozdělení
Test má 20 otázek, každá s 4 možnostmi. Pokud tipujete náhodně:
a) Jaká je pravděpodobnost, že správně odpovíte alespoň na 10 otázek?
b) Kolik otázek průměrně zodpovíte správně?
:::
::: {.callout-note icon=false}
## Cvičení 4: Softmax
Implementujte "top-k sampling" - místo vzorkování ze všech slov, vzorkujte jen z $k$ nejpravděpodobnějších. Porovnejte výsledky pro různá $k$.
:::
::: {.callout-note icon=false}
## Cvičení 5: Generátor textu
Rozšiřte bigramový model z příkladu 3 o další slova a přechody. Vygenerujte 10 vět a porovnejte s originálním modelem.
:::
::: {.callout-note icon=false}
## Cvičení 6: Zákon velkých čísel
Simulujte hod kostkou a sledujte, jak se průměr přibližuje střední hodnotě se zvyšujícím se počtem hodů. Vykreslete graf konvergence.
:::
## Shrnutí
::: {.callout-tip}
## Co jsme se naučili
1. **Náhodná veličina** přiřazuje číselné hodnoty náhodným výsledkům
2. **Diskrétní veličina** nabývá izolovaných hodnot, **spojitá** libovolných z intervalu
3. **Střední hodnota** $E[X] = \sum_x x \cdot P(X=x)$ je vážený průměr
4. **Rozptyl** $\text{Var}(X) = E[(X-\mu)^2]$ měří rozptýlenost hodnot
5. **Bernoulliho** rozdělení popisuje jeden pokus s dvěma výsledky
6. **Binomické** rozdělení počítá úspěchy v $n$ pokusech
7. **Kategorické** rozdělení zobecňuje na více výsledků (klíčové pro jazykové modely)
8. **Softmax** převádí čísla na pravděpodobnosti s parametrem teploty
:::
::: {.callout-important}
## Klíčové pojmy
- **Náhodná veličina**: $X: \Omega \to \mathbb{R}$
- **Střední hodnota**: $E[X] = \sum_x x \cdot P(X=x)$
- **Rozptyl**: $\text{Var}(X) = E[X^2] - (E[X])^2$
- **Směrodatná odchylka**: $\sigma = \sqrt{\text{Var}(X)}$
- **Softmax**: $\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_j e^{z_j}}$
:::
V další kapitole se podíváme na nejdůležitější spojité rozdělení - normální (Gaussovo) rozdělení, které hraje klíčovou roli v inicializaci neuronových sítí a mnoha dalších oblastech.