# Normální rozdělení {#sec-normalni-rozdeleni}
## Motivace: Proč je Gaussovka všude?
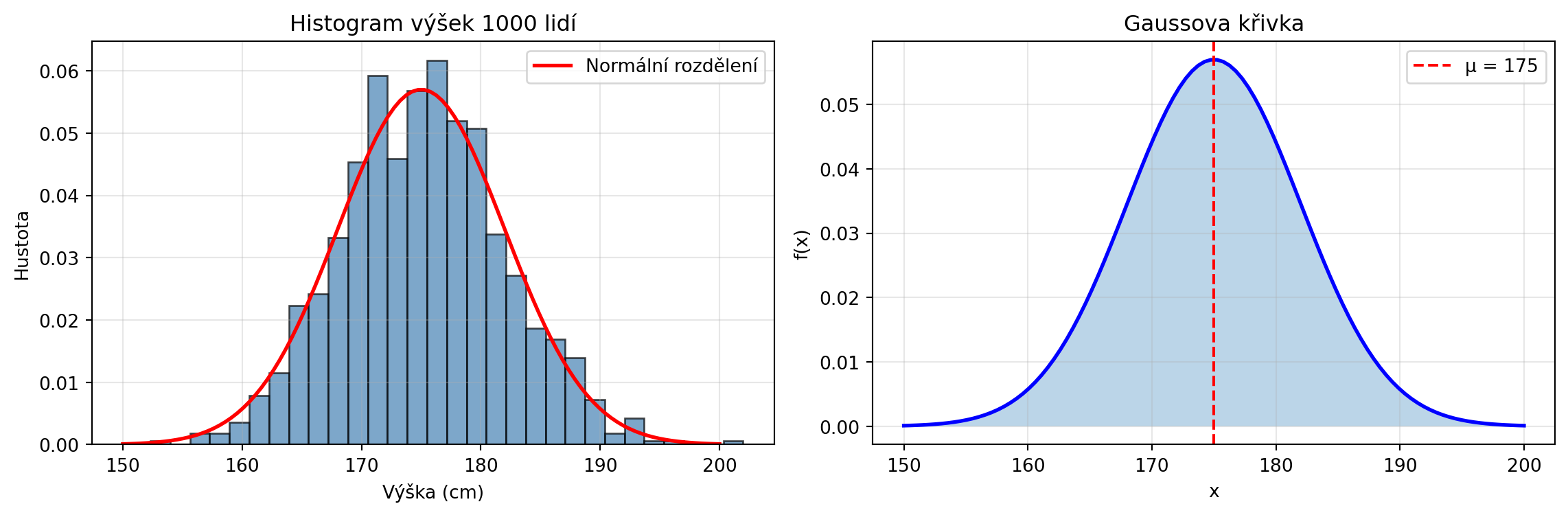
Když změříte výšku 1000 lidí a nakreslíte histogram, dostanete charakteristický tvar - zvon. Podobný tvar uvidíte u:
- Chyb měření
- IQ skóre
- Hmotnosti novorozenců
- Denních výnosů akcií
- **Vah neuronových sítí po inicializaci**
Tomuto "zvonovému" rozdělení říkáme **normální** nebo **Gaussovo** rozdělení. Je to nejdůležitější spojité rozdělení v celé statistice a strojovém učení.
```{python}
import numpy as np
import matplotlib.pyplot as plt
from math import sqrt, pi, exp, erf
# Pomocné funkce pro normální rozdělení (bez scipy)
def norm_pdf(x, mu=0, sigma=1):
"""Hustota normálního rozdělení."""
return (1 / (sigma * sqrt(2 * pi))) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)
def norm_cdf(x, mu=0, sigma=1):
"""Distribuční funkce normálního rozdělení."""
z = (x - mu) / (sigma * sqrt(2))
# Použijeme numpy pro vektorizaci
if isinstance(x, np.ndarray):
return 0.5 * (1 + np.array([erf(zi) for zi in z.flatten()]).reshape(x.shape))
return 0.5 * (1 + erf(z))
def norm_ppf(p, mu=0, sigma=1):
"""Kvantilová funkce (inverzní CDF) - aproximace."""
# Aproximace pomocí Abramowitz and Stegun
def inv_erf(x):
a = 0.147
ln_term = np.log(1 - x**2)
term1 = (2 / (np.pi * a)) + ln_term / 2
return np.sign(x) * np.sqrt(np.sqrt(term1**2 - ln_term / a) - term1)
return mu + sigma * sqrt(2) * inv_erf(2 * p - 1)
# Příklad: Simulace výšek
np.random.seed(42)
vysky = np.random.normal(175, 7, 1000) # μ=175cm, σ=7cm
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
# Histogram
ax1.hist(vysky, bins=30, density=True, alpha=0.7, color='steelblue', edgecolor='black')
x = np.linspace(150, 200, 100)
ax1.plot(x, norm_pdf(x, 175, 7), 'r-', lw=2, label='Normální rozdělení')
ax1.set_xlabel('Výška (cm)')
ax1.set_ylabel('Hustota')
ax1.set_title('Histogram výšek 1000 lidí')
ax1.legend()
ax1.grid(True, alpha=0.3)
# Klasická Gaussovka
ax2.plot(x, norm_pdf(x, 175, 7), 'b-', lw=2)
ax2.fill_between(x, norm_pdf(x, 175, 7), alpha=0.3)
ax2.axvline(x=175, color='red', linestyle='--', label='μ = 175')
ax2.set_xlabel('x')
ax2.set_ylabel('f(x)')
ax2.set_title('Gaussova křivka')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
## Definice normálního rozdělení
::: {.callout-note}
## Definice: Normální rozdělení
Náhodná veličina $X$ má **normální rozdělení** s parametry $\mu$ (střední hodnota) a $\sigma^2$ (rozptyl), píšeme $X \sim \mathcal{N}(\mu, \sigma^2)$, pokud má hustotu pravděpodobnosti:
$$f(x) = \frac{1}{\sigma\sqrt{2\pi}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$$
:::
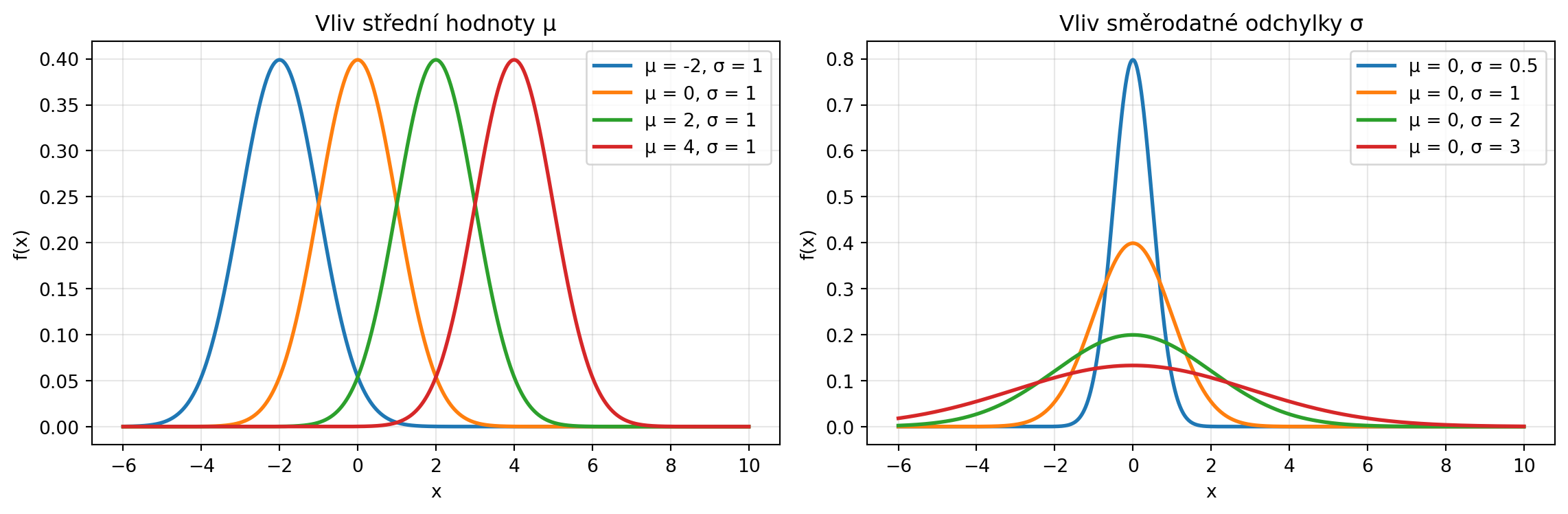
Parametry mají jasný význam:
- $\mu$ = střed (vrchol) křivky
- $\sigma$ = šířka křivky (směrodatná odchylka)
```{python}
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-6, 10, 1000)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
# Různé střední hodnoty
for mu in [-2, 0, 2, 4]:
ax1.plot(x, norm_pdf(x, mu, 1), lw=2, label=f'μ = {mu}, σ = 1')
ax1.set_xlabel('x')
ax1.set_ylabel('f(x)')
ax1.set_title('Vliv střední hodnoty μ')
ax1.legend()
ax1.grid(True, alpha=0.3)
# Různé rozptyly
for sigma in [0.5, 1, 2, 3]:
ax2.plot(x, norm_pdf(x, 0, sigma), lw=2, label=f'μ = 0, σ = {sigma}')
ax2.set_xlabel('x')
ax2.set_ylabel('f(x)')
ax2.set_title('Vliv směrodatné odchylky σ')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
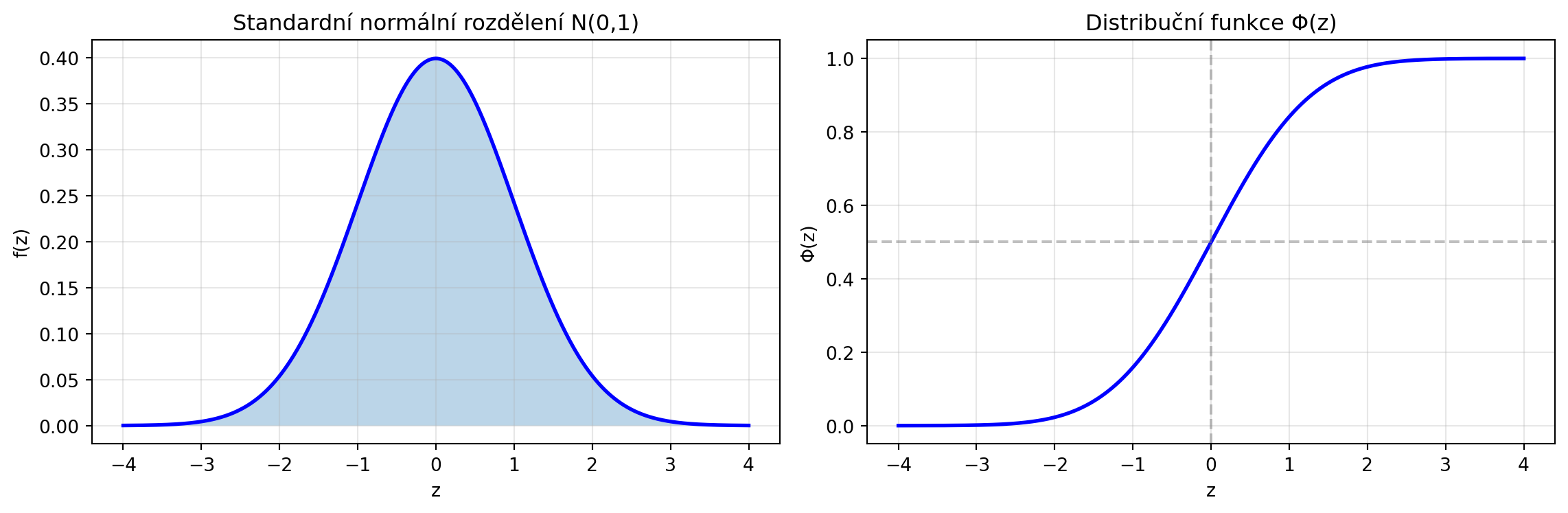
## Standardní normální rozdělení
Speciální případ s $\mu = 0$ a $\sigma = 1$ se nazývá **standardní normální rozdělení** a značí se $\mathcal{N}(0, 1)$:
$$f(z) = \frac{1}{\sqrt{2\pi}} e^{-z^2/2}$$
```{python}
import numpy as np
import matplotlib.pyplot as plt
z = np.linspace(-4, 4, 1000)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
# Hustota
ax1.plot(z, norm_pdf(z, 0, 1), 'b-', lw=2)
ax1.fill_between(z, norm_pdf(z, 0, 1), alpha=0.3)
ax1.set_xlabel('z')
ax1.set_ylabel('f(z)')
ax1.set_title('Standardní normální rozdělení N(0,1)')
ax1.grid(True, alpha=0.3)
# Distribuční funkce
ax2.plot(z, norm_cdf(z, 0, 1), 'b-', lw=2)
ax2.axhline(y=0.5, color='gray', linestyle='--', alpha=0.5)
ax2.axvline(x=0, color='gray', linestyle='--', alpha=0.5)
ax2.set_xlabel('z')
ax2.set_ylabel('Φ(z)')
ax2.set_title('Distribuční funkce Φ(z)')
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("Důležité hodnoty distribuční funkce:")
for z_val in [-2, -1, 0, 1, 2]:
print(f"Φ({z_val:2d}) = {norm_cdf(z_val, 0, 1):.4f}")
```
### Standardizace
Libovolnou normální veličinu můžeme převést na standardní pomocí **standardizace** (z-skóre):
::: {.callout-note}
## Z-skóre
Pokud $X \sim \mathcal{N}(\mu, \sigma^2)$, pak:
$$Z = \frac{X - \mu}{\sigma} \sim \mathcal{N}(0, 1)$$
Z-skóre říká, kolik směrodatných odchylek je hodnota od průměru.
:::
```{python}
# Příklad: IQ má μ=100, σ=15
mu, sigma = 100, 15
hodnota = 130
z_score = (hodnota - mu) / sigma
print(f"IQ = {hodnota}")
print(f"Z-skóre = ({hodnota} - {mu}) / {sigma} = {z_score:.2f}")
print(f"IQ {hodnota} je {z_score:.2f} směrodatných odchylek nad průměrem")
# Kolik procent má nižší IQ?
percentil = norm_cdf(z_score)
print(f"\nApproximativně {percentil:.1%} lidí má IQ nižší než {hodnota}")
```
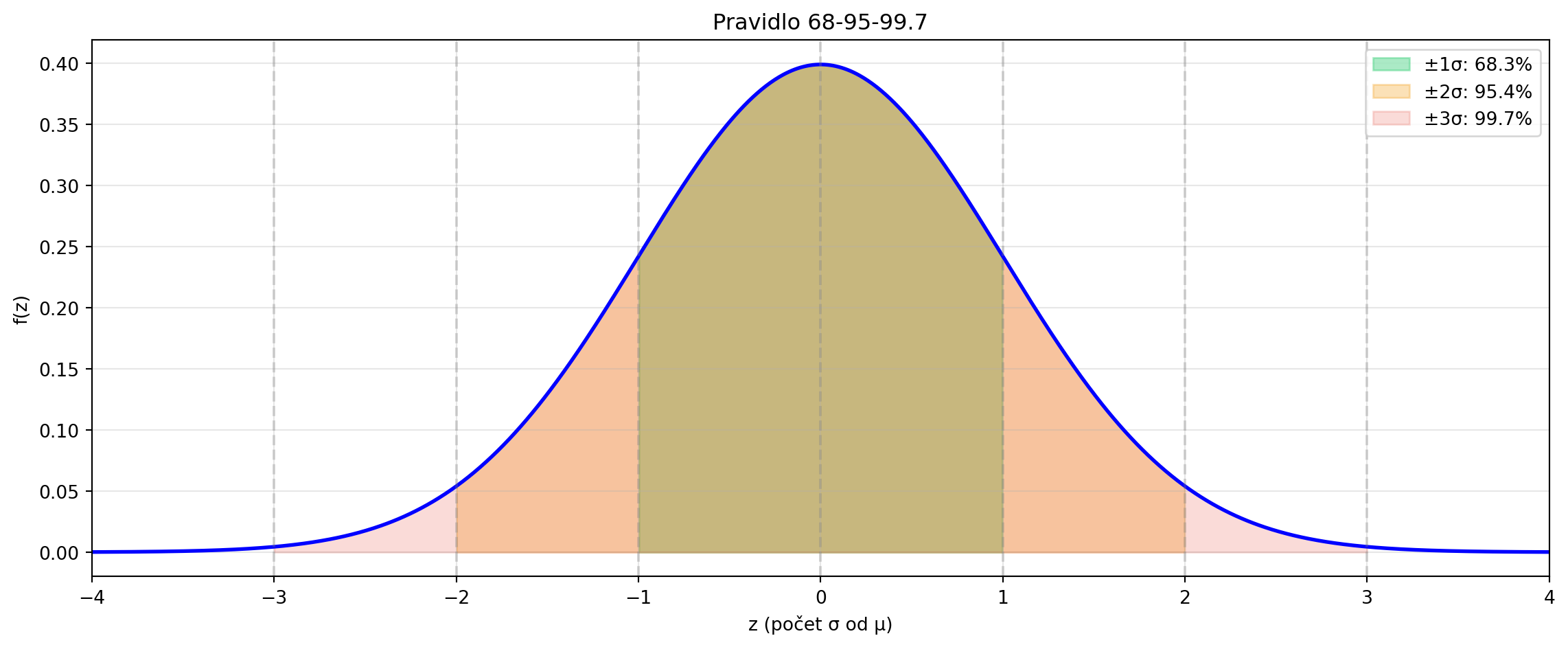
## Pravidlo 68-95-99.7
Normální rozdělení má důležitou vlastnost - většina hodnot leží blízko střední hodnoty:
```{python}
# Pravděpodobnosti pro intervaly
import numpy as np
import matplotlib.pyplot as plt
P_1sigma = norm_cdf(1) - norm_cdf(-1)
P_2sigma = norm_cdf(2) - norm_cdf(-2)
P_3sigma = norm_cdf(3) - norm_cdf(-3)
print("Pravidlo 68-95-99.7:")
print(f"P(μ - σ ≤ X ≤ μ + σ) = {P_1sigma:.4f} ≈ 68%")
print(f"P(μ - 2σ ≤ X ≤ μ + 2σ) = {P_2sigma:.4f} ≈ 95%")
print(f"P(μ - 3σ ≤ X ≤ μ + 3σ) = {P_3sigma:.4f} ≈ 99.7%")
# Vizualizace
fig, ax = plt.subplots(figsize=(12, 5))
z = np.linspace(-4, 4, 1000)
# Základní křivka
ax.plot(z, norm_pdf(z), 'b-', lw=2)
# Vyplnění oblastí
for sigma_range, color, alpha in [(1, '#2ecc71', 0.4), (2, '#f39c12', 0.3), (3, '#e74c3c', 0.2)]:
mask = (z >= -sigma_range) & (z <= sigma_range)
ax.fill_between(z[mask], norm_pdf(z[mask]), alpha=alpha, color=color,
label=f'±{sigma_range}σ: {norm_cdf(sigma_range) - norm_cdf(-sigma_range):.1%}')
ax.set_xlabel('z (počet σ od μ)')
ax.set_ylabel('f(z)')
ax.set_title('Pravidlo 68-95-99.7')
ax.legend(loc='upper right')
ax.set_xlim(-4, 4)
ax.grid(True, alpha=0.3)
# Popisky os
for i in range(-3, 4):
ax.axvline(x=i, color='gray', linestyle='--', alpha=0.3)
plt.tight_layout()
plt.show()
```
## Centrální limitní věta
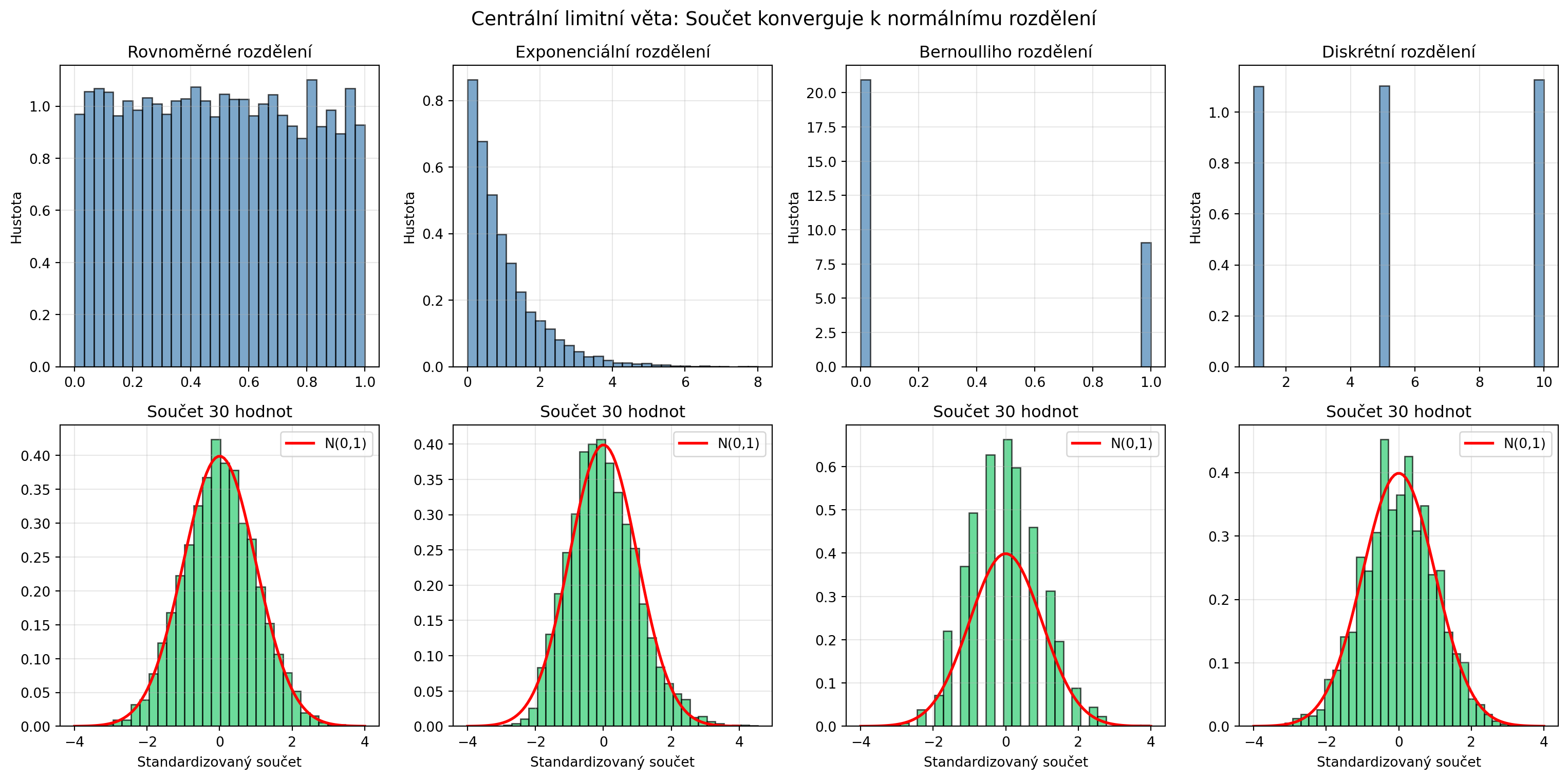
Proč je normální rozdělení tak všudypřítomné? Díky **centrální limitní větě**:
::: {.callout-important}
## Centrální limitní věta (CLV)
Součet (nebo průměr) velkého počtu nezávislých náhodných veličin má přibližně normální rozdělení, **bez ohledu na jejich původní rozdělení**.
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
fig, axes = plt.subplots(2, 4, figsize=(16, 8))
# Různá původní rozdělení
rozdeleni = [
('Rovnoměrné', lambda n: np.random.uniform(0, 1, n)),
('Exponenciální', lambda n: np.random.exponential(1, n)),
('Bernoulliho', lambda n: np.random.binomial(1, 0.3, n)),
('Diskrétní', lambda n: np.random.choice([1, 5, 10], n))
]
for col, (nazev, generator) in enumerate(rozdeleni):
# Původní rozdělení
vzorky = generator(10000)
axes[0, col].hist(vzorky, bins=30, density=True, alpha=0.7, color='steelblue', edgecolor='black')
axes[0, col].set_title(f'{nazev} rozdělení')
axes[0, col].set_ylabel('Hustota')
axes[0, col].grid(True, alpha=0.3)
# Součet 30 hodnot (mnoho opakování)
n_sum = 30
n_experiments = 5000
soucty = np.array([generator(n_sum).sum() for _ in range(n_experiments)])
# Standardizace
soucty_std = (soucty - soucty.mean()) / soucty.std()
axes[1, col].hist(soucty_std, bins=30, density=True, alpha=0.7, color='#2ecc71', edgecolor='black')
# Přidání normální křivky
x = np.linspace(-4, 4, 100)
axes[1, col].plot(x, norm_pdf(x), 'r-', lw=2, label='N(0,1)')
axes[1, col].set_title(f'Součet {n_sum} hodnot')
axes[1, col].set_xlabel('Standardizovaný součet')
axes[1, col].legend()
axes[1, col].grid(True, alpha=0.3)
plt.suptitle('Centrální limitní věta: Součet konverguje k normálnímu rozdělení', fontsize=14)
plt.tight_layout()
plt.show()
```
## Aplikace v strojovém učení
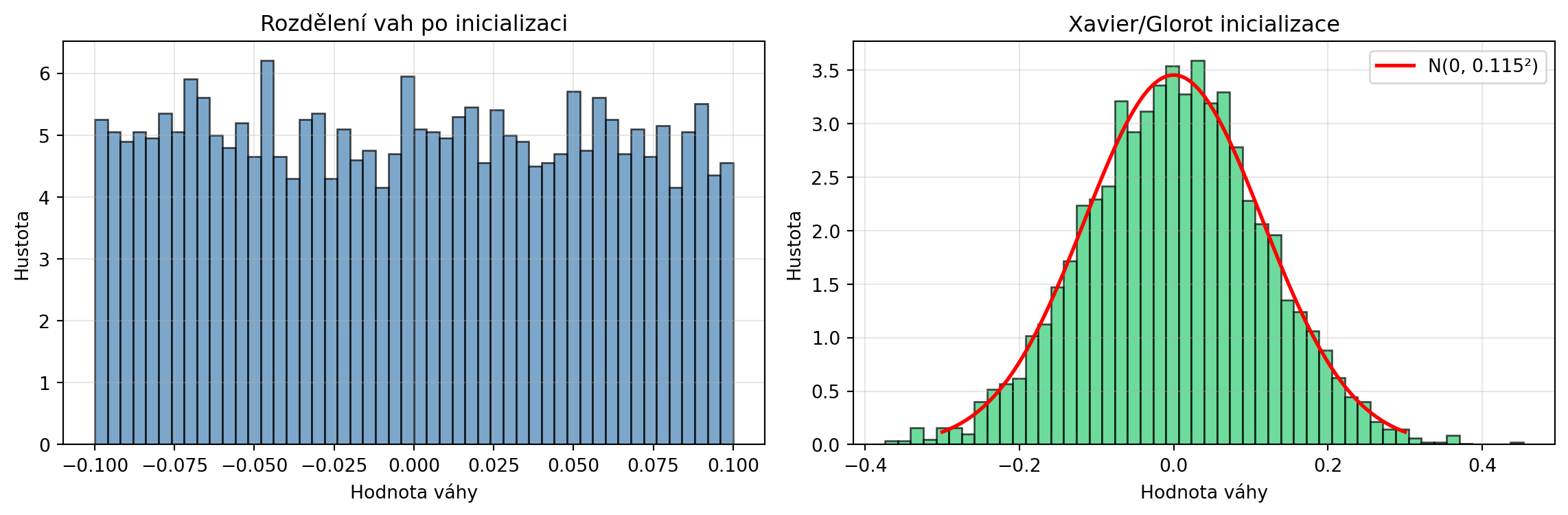
### Inicializace vah neuronových sítí
Váhy neuronových sítí se typicky inicializují z normálního rozdělení:
```{python}
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
# Lineární vrstva s výchozí inicializací
vrstva = nn.Linear(100, 50)
# Váhy jsou inicializovány z rovnoměrného rozdělení (Kaiming/He)
# ale můžeme použít normální rozdělení
vahy = vrstva.weight.detach().numpy().flatten()
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
# Histogram vah
ax1.hist(vahy, bins=50, density=True, alpha=0.7, color='steelblue', edgecolor='black')
ax1.set_xlabel('Hodnota váhy')
ax1.set_ylabel('Hustota')
ax1.set_title('Rozdělení vah po inicializaci')
ax1.grid(True, alpha=0.3)
# Normální inicializace (Xavier/Glorot)
np.random.seed(42)
n_in, n_out = 100, 50
std = np.sqrt(2.0 / (n_in + n_out)) # Xavier inicializace
vahy_xavier = np.random.normal(0, std, n_in * n_out)
ax2.hist(vahy_xavier, bins=50, density=True, alpha=0.7, color='#2ecc71', edgecolor='black')
x = np.linspace(-0.3, 0.3, 100)
ax2.plot(x, norm_pdf(x, 0, std), 'r-', lw=2, label=f'N(0, {std:.3f}²)')
ax2.set_xlabel('Hodnota váhy')
ax2.set_ylabel('Hustota')
ax2.set_title('Xavier/Glorot inicializace')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print(f"Xavier inicializace pro vrstvu {n_in}→{n_out}:")
print(f"σ = √(2/(n_in + n_out)) = √(2/{n_in + n_out}) = {std:.4f}")
```
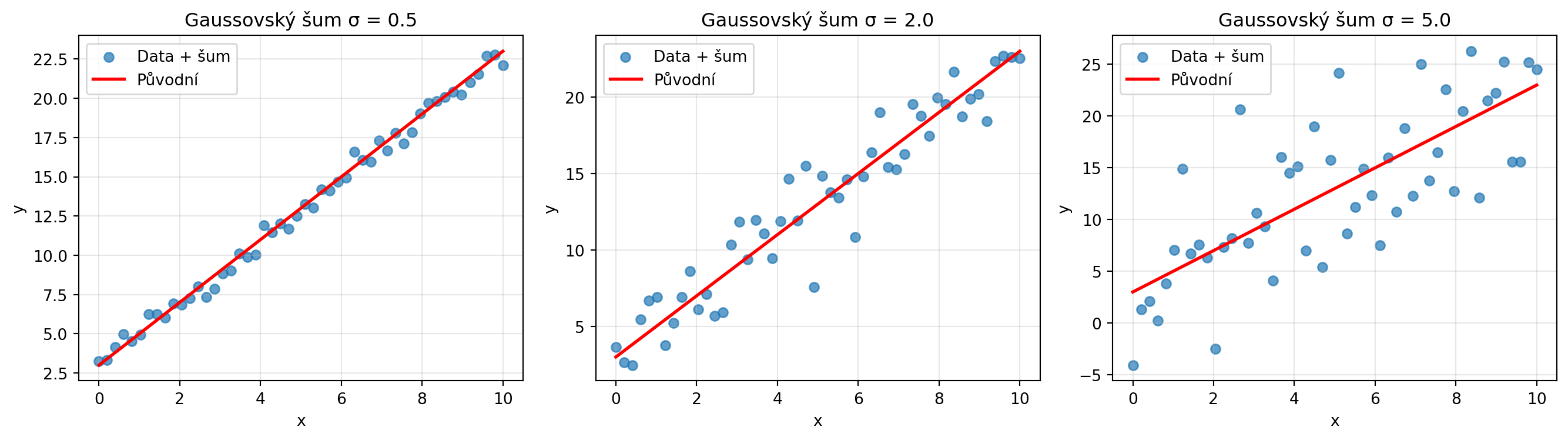
### Přidávání šumu
Normální šum se používá v mnoha technikách:
```{python}
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
# Příklad: Data augmentace přidáním šumu
x_original = np.linspace(0, 10, 50)
y_original = 2 * x_original + 3
# Různé úrovně šumu
fig, axes = plt.subplots(1, 3, figsize=(14, 4))
sigmy = [0.5, 2.0, 5.0]
for ax, sigma in zip(axes, sigmy):
sum = np.random.normal(0, sigma, len(y_original))
y_noisy = y_original + sum
ax.scatter(x_original, y_noisy, alpha=0.7, label='Data + šum')
ax.plot(x_original, y_original, 'r-', lw=2, label='Původní')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title(f'Gaussovský šum σ = {sigma}')
ax.legend()
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
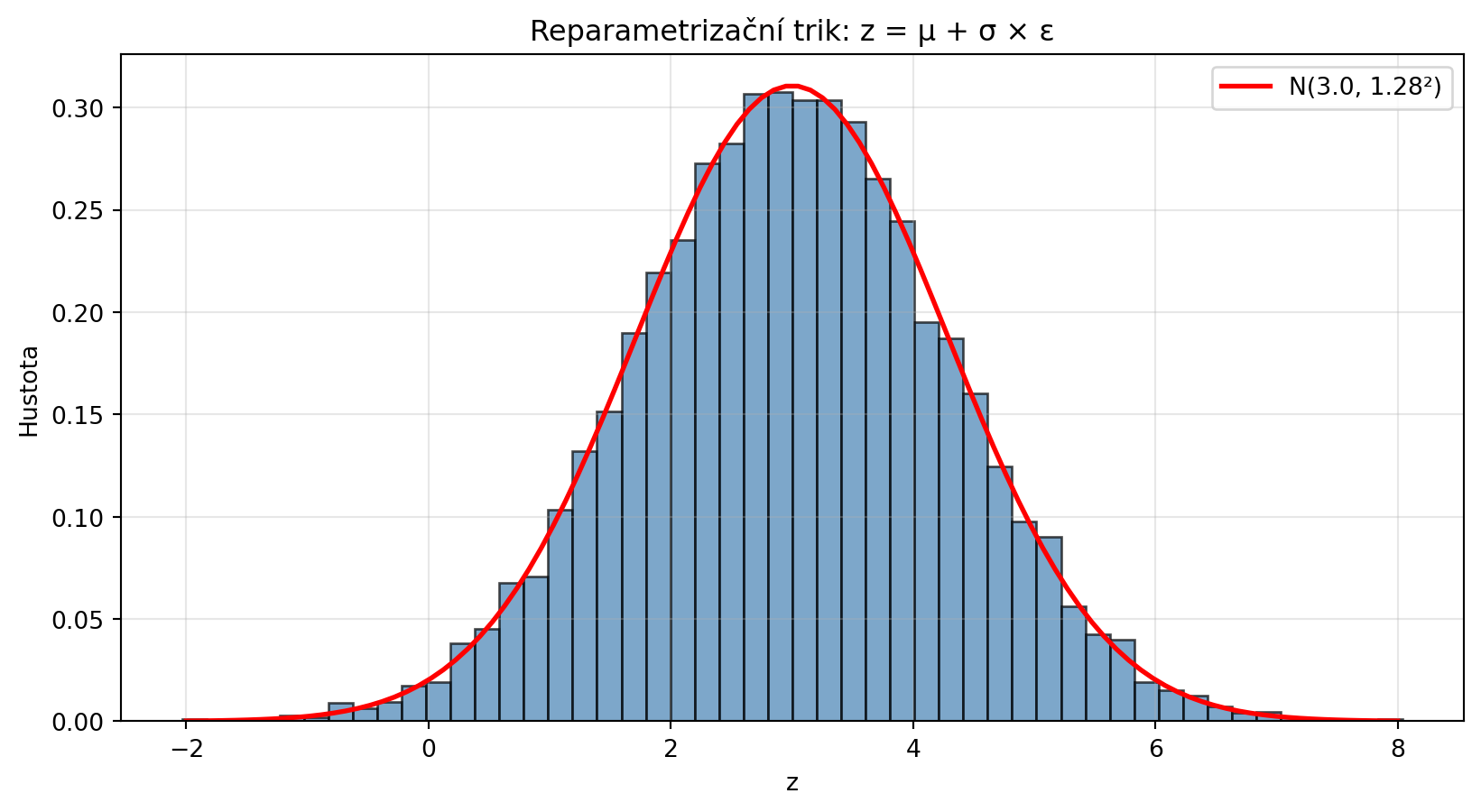
### Reparametrizační trik
V variačních autoencodérech se používá **reparametrizační trik** pro vzorkování z normálního rozdělení:
```{python}
import numpy as np
import matplotlib.pyplot as plt
def reparametrizace(mu, log_var, n_samples=1):
"""
Vzorkuje z N(μ, σ²) pomocí reparametrizačního triku.
z = μ + σ * ε, kde ε ~ N(0, 1)
"""
std = np.exp(0.5 * log_var) # σ = exp(log_var / 2)
epsilon = np.random.normal(0, 1, n_samples)
return mu + std * epsilon
# Příklad
mu = 3.0
log_var = 0.5 # log(σ²)
sigma = np.exp(0.5 * log_var)
vzorky = reparametrizace(mu, log_var, 10000)
plt.figure(figsize=(10, 5))
plt.hist(vzorky, bins=50, density=True, alpha=0.7, color='steelblue', edgecolor='black')
x = np.linspace(-2, 8, 100)
plt.plot(x, norm_pdf(x, mu, sigma), 'r-', lw=2, label=f'N({mu}, {sigma:.2f}²)')
plt.xlabel('z')
plt.ylabel('Hustota')
plt.title('Reparametrizační trik: z = μ + σ × ε')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
print(f"μ = {mu}, log(σ²) = {log_var}, σ = {sigma:.4f}")
print(f"Empirický průměr: {np.mean(vzorky):.4f}")
print(f"Empirická σ: {np.std(vzorky):.4f}")
```
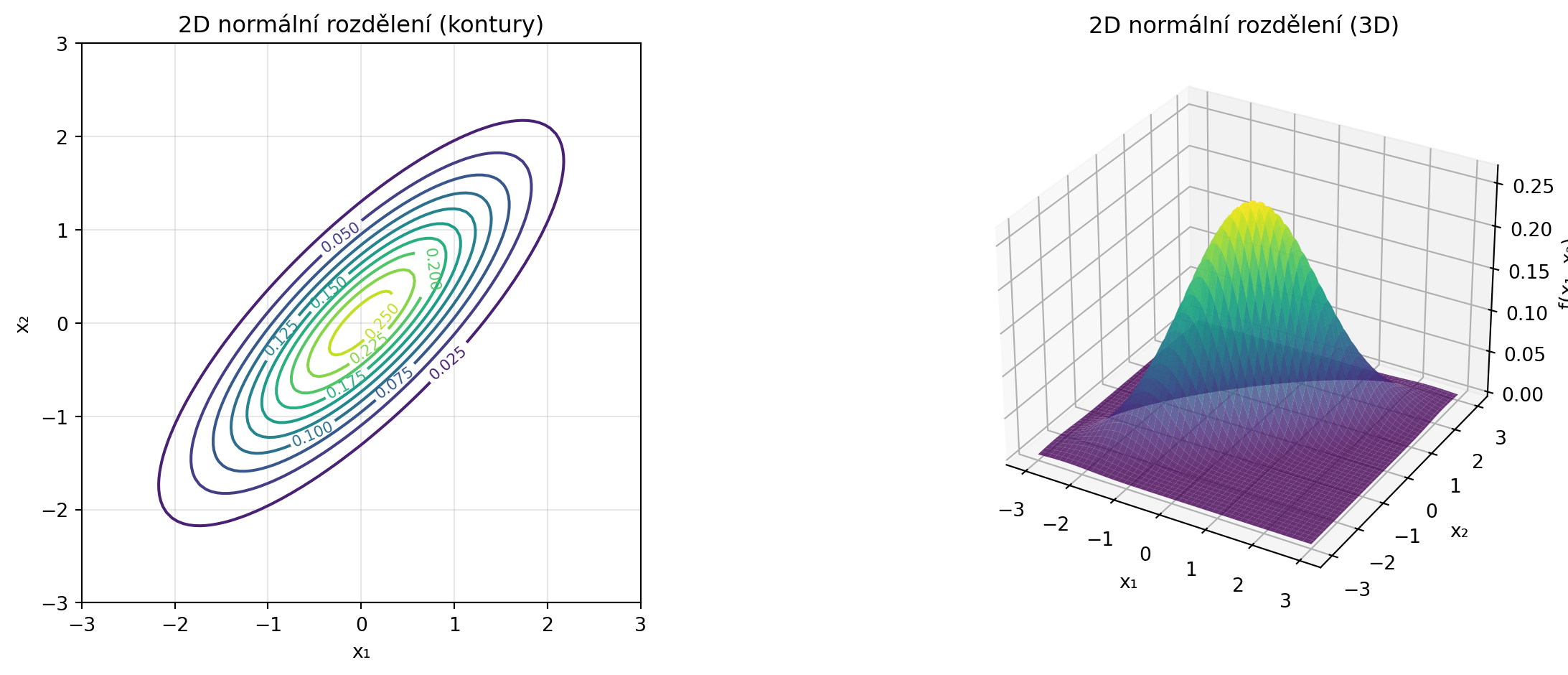
## Vícerozměrné normální rozdělení
V praxi často pracujeme s vektory, které mají normální rozdělení:
::: {.callout-note}
## Vícerozměrné normální rozdělení
Vektor $\mathbf{x} \in \mathbb{R}^n$ má vícerozměrné normální rozdělení $\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$, kde:
- $\boldsymbol{\mu}$ je vektor středních hodnot
- $\boldsymbol{\Sigma}$ je kovarianční matice
Hustota je:
$$f(\mathbf{x}) = \frac{1}{\sqrt{(2\pi)^n |\boldsymbol{\Sigma}|}} \exp\left(-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1}(\mathbf{x}-\boldsymbol{\mu})\right)$$
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
def multivariate_normal_pdf(pos, mu, sigma):
"""Hustota vícerozměrného normálního rozdělení."""
mu = np.array(mu)
sigma = np.array(sigma)
n = len(mu)
det = np.linalg.det(sigma)
inv = np.linalg.inv(sigma)
norm_const = 1.0 / (np.sqrt((2*np.pi)**n * det))
# Reshape pro vektorizovaný výpočet
diff = pos - mu
# Mahalanobisova vzdálenost
result = np.zeros(pos.shape[:-1])
for i in range(pos.shape[0]):
for j in range(pos.shape[1]):
d = diff[i, j]
result[i, j] = norm_const * np.exp(-0.5 * d @ inv @ d)
return result
# 2D normální rozdělení
mu = [0, 0]
sigma = [[1, 0.8],
[0.8, 1]] # Korelované proměnné
# Vytvoření mřížky
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
pos = np.dstack((X, Y))
# Hustota
Z = multivariate_normal_pdf(pos, mu, sigma)
fig = plt.figure(figsize=(14, 5))
# Kontury
ax1 = fig.add_subplot(121)
contour = ax1.contour(X, Y, Z, levels=10, cmap='viridis')
ax1.clabel(contour, inline=True, fontsize=8)
ax1.set_xlabel('x₁')
ax1.set_ylabel('x₂')
ax1.set_title('2D normální rozdělení (kontury)')
ax1.set_aspect('equal')
ax1.grid(True, alpha=0.3)
# 3D povrch
ax2 = fig.add_subplot(122, projection='3d')
ax2.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
ax2.set_xlabel('x₁')
ax2.set_ylabel('x₂')
ax2.set_zlabel('f(x₁, x₂)')
ax2.set_title('2D normální rozdělení (3D)')
plt.tight_layout()
plt.show()
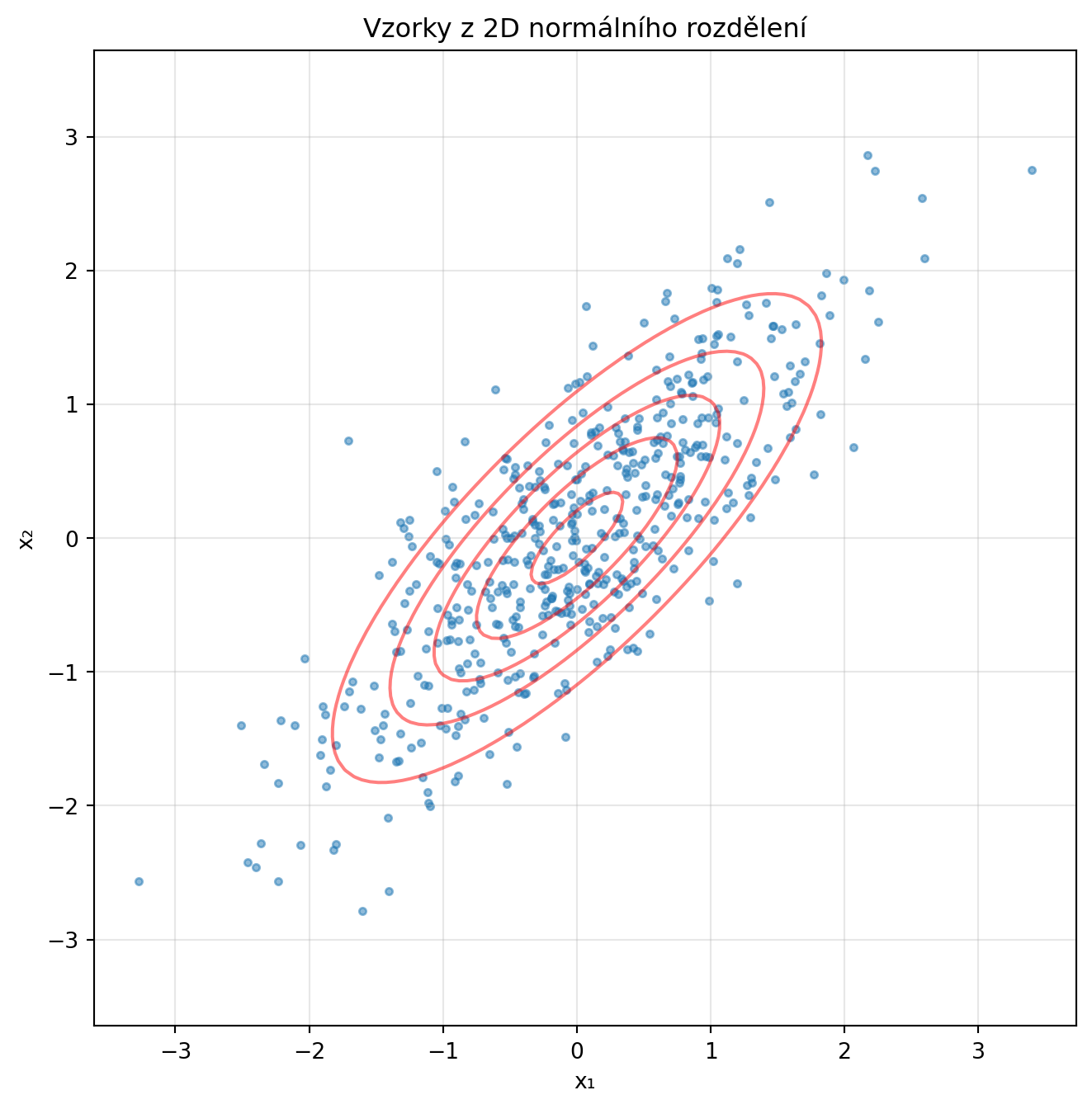
# Vzorkování
np.random.seed(42)
vzorky = np.random.multivariate_normal(mu, sigma, 500)
plt.figure(figsize=(8, 8))
plt.scatter(vzorky[:, 0], vzorky[:, 1], alpha=0.5, s=10)
plt.contour(X, Y, Z, levels=5, colors='red', alpha=0.5)
plt.xlabel('x₁')
plt.ylabel('x₂')
plt.title('Vzorky z 2D normálního rozdělení')
plt.axis('equal')
plt.grid(True, alpha=0.3)
plt.show()
```
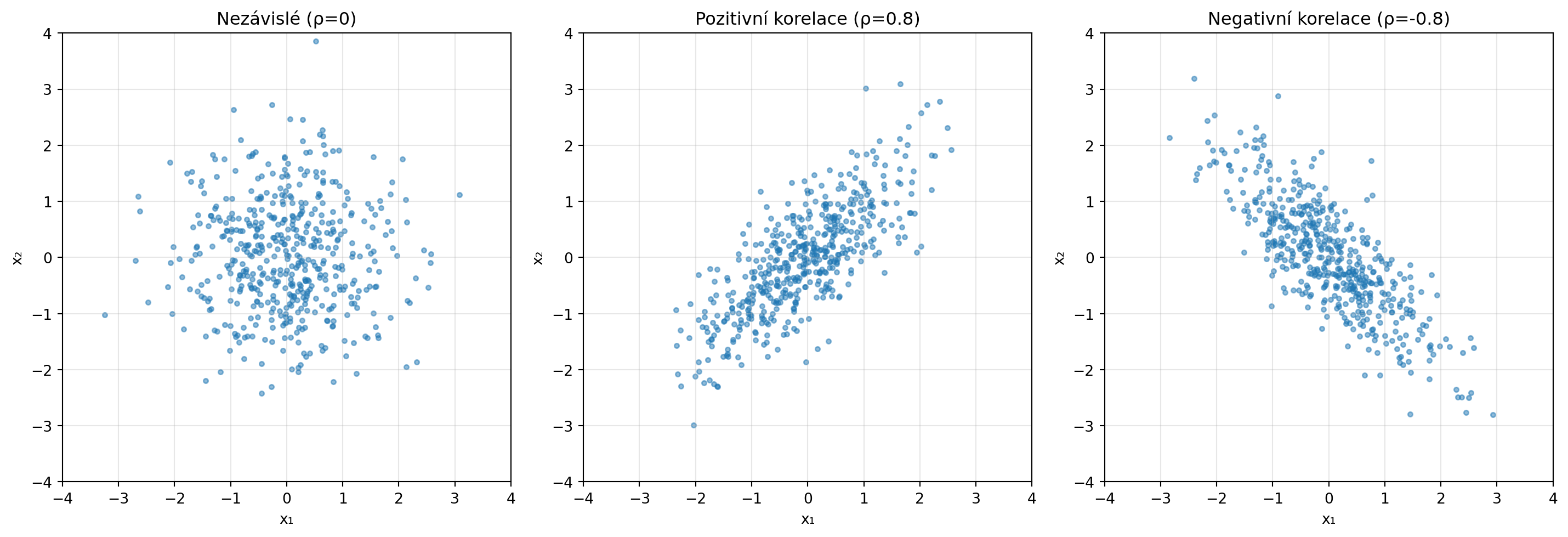
### Nezávislé vs korelované proměnné
```{python}
import numpy as np
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
kovariance = [
[[1, 0], [0, 1]], # Nezávislé
[[1, 0.8], [0.8, 1]], # Pozitivně korelované
[[1, -0.8], [-0.8, 1]] # Negativně korelované
]
titulky = ['Nezávislé (ρ=0)', 'Pozitivní korelace (ρ=0.8)', 'Negativní korelace (ρ=-0.8)']
np.random.seed(42)
for ax, cov, titulek in zip(axes, kovariance, titulky):
vzorky = np.random.multivariate_normal([0, 0], cov, 500)
ax.scatter(vzorky[:, 0], vzorky[:, 1], alpha=0.5, s=10)
ax.set_xlabel('x₁')
ax.set_ylabel('x₂')
ax.set_title(titulek)
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
## Řešené příklady
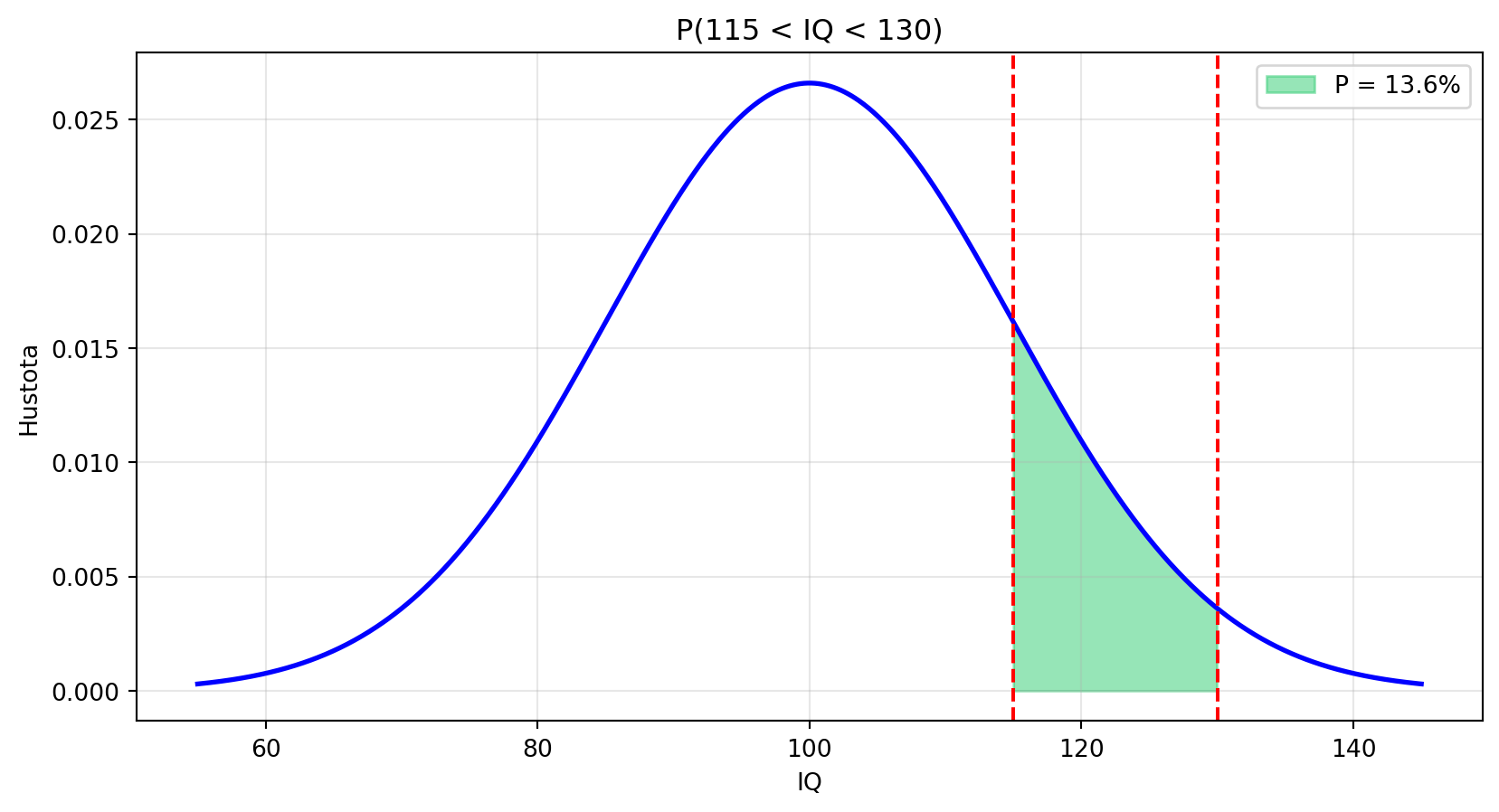
### Příklad 1: Výpočty s normálním rozdělením
**Zadání**: IQ má normální rozdělení s μ=100 a σ=15. Jaká je pravděpodobnost, že náhodně vybraná osoba má IQ mezi 115 a 130?
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
mu, sigma = 100, 15
# P(115 < X < 130)
P = norm_cdf(130, mu, sigma) - norm_cdf(115, mu, sigma)
print(f"P(115 < IQ < 130) = {P:.4f} = {P:.1%}")
# Vizualizace
x = np.linspace(55, 145, 1000)
plt.figure(figsize=(10, 5))
plt.plot(x, norm_pdf(x, mu, sigma), 'b-', lw=2)
plt.fill_between(x[(x >= 115) & (x <= 130)],
norm_pdf(x[(x >= 115) & (x <= 130)], mu, sigma),
alpha=0.5, color='#2ecc71', label=f'P = {P:.1%}')
plt.axvline(x=115, color='red', linestyle='--')
plt.axvline(x=130, color='red', linestyle='--')
plt.xlabel('IQ')
plt.ylabel('Hustota')
plt.title('P(115 < IQ < 130)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
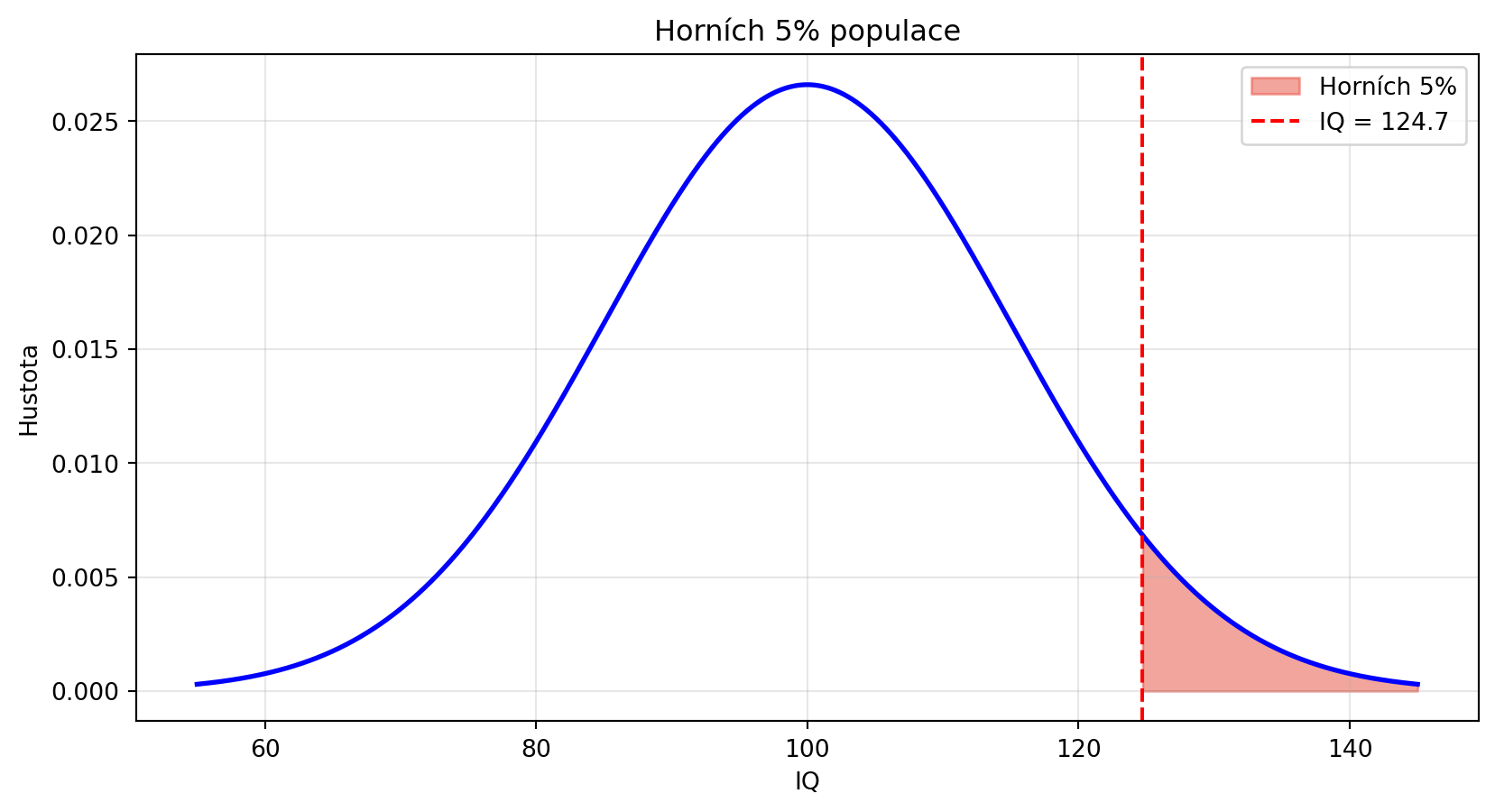
### Příklad 2: Inverzní problém (kvantily)
**Zadání**: Jaké IQ má horních 5 % populace?
**Řešení**:
```{python}
# Hledáme x takové, že P(X > x) = 0.05
# Tedy P(X ≤ x) = 0.95
import matplotlib.pyplot as plt
kvantil_95 = norm_ppf(0.95, mu, sigma)
print(f"95. percentil IQ: {kvantil_95:.1f}")
print(f"Horních 5% má IQ vyšší než {kvantil_95:.1f}")
# Vizualizace
plt.figure(figsize=(10, 5))
plt.plot(x, norm_pdf(x, mu, sigma), 'b-', lw=2)
plt.fill_between(x[x >= kvantil_95],
norm_pdf(x[x >= kvantil_95], mu, sigma),
alpha=0.5, color='#e74c3c', label=f'Horních 5%')
plt.axvline(x=kvantil_95, color='red', linestyle='--', label=f'IQ = {kvantil_95:.1f}')
plt.xlabel('IQ')
plt.ylabel('Hustota')
plt.title('Horních 5% populace')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
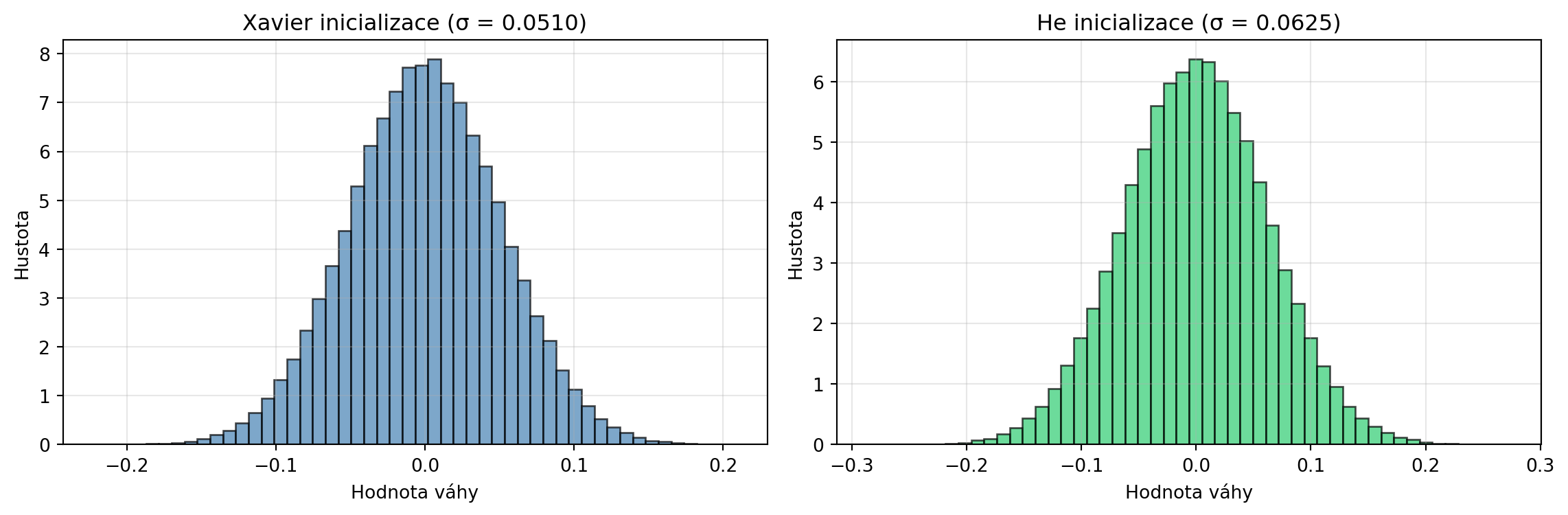
### Příklad 3: Inicializace vah v PyTorch
**Zadání**: Implementujte Xavier a He inicializaci vah.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
def xavier_init(n_in, n_out):
"""Xavier/Glorot inicializace."""
std = np.sqrt(2.0 / (n_in + n_out))
return torch.randn(n_out, n_in) * std
def he_init(n_in, n_out):
"""He/Kaiming inicializace (pro ReLU)."""
std = np.sqrt(2.0 / n_in)
return torch.randn(n_out, n_in) * std
n_in, n_out = 512, 256
W_xavier = xavier_init(n_in, n_out)
W_he = he_init(n_in, n_out)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.hist(W_xavier.numpy().flatten(), bins=50, density=True, alpha=0.7, color='steelblue', edgecolor='black')
ax1.set_title(f'Xavier inicializace (σ = {W_xavier.std():.4f})')
ax1.set_xlabel('Hodnota váhy')
ax1.set_ylabel('Hustota')
ax1.grid(True, alpha=0.3)
ax2.hist(W_he.numpy().flatten(), bins=50, density=True, alpha=0.7, color='#2ecc71', edgecolor='black')
ax2.set_title(f'He inicializace (σ = {W_he.std():.4f})')
ax2.set_xlabel('Hodnota váhy')
ax2.set_ylabel('Hustota')
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print(f"Xavier: σ = √(2/{n_in+n_out}) = {np.sqrt(2/(n_in+n_out)):.4f}")
print(f"He: σ = √(2/{n_in}) = {np.sqrt(2/n_in):.4f}")
```
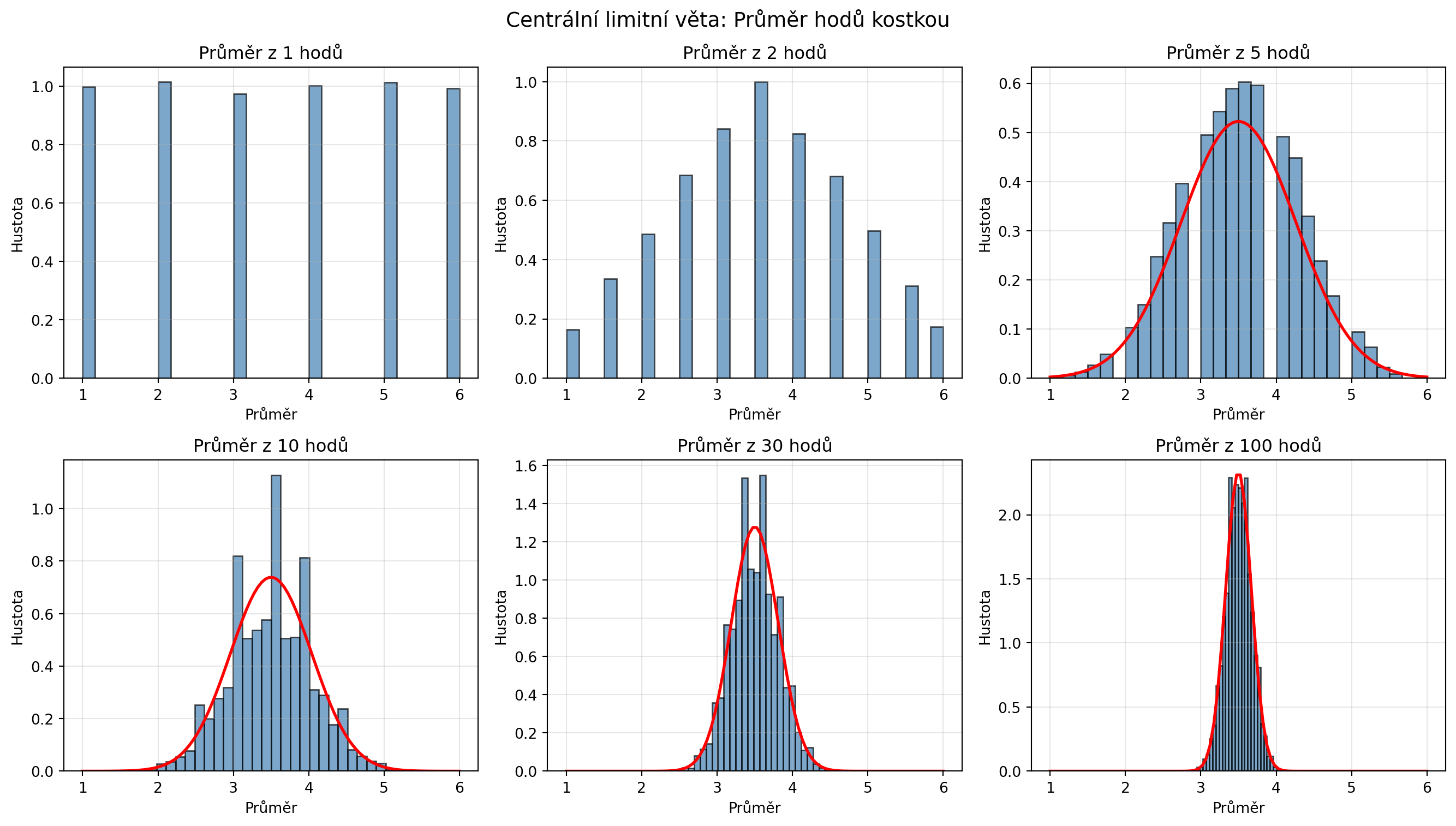
### Příklad 4: Ověření centrální limitní věty
**Zadání**: Simulujte CLV pro hody kostkou.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
n_experimenty = 10000
pocty_hodu = [1, 2, 5, 10, 30, 100]
fig, axes = plt.subplots(2, 3, figsize=(14, 8))
axes = axes.flatten()
for ax, n_hodu in zip(axes, pocty_hodu):
# Simulace: n_hodu hodů kostkou, opakujeme n_experimenty krát
prumery = []
for _ in range(n_experimenty):
hody = np.random.randint(1, 7, n_hodu)
prumery.append(np.mean(hody))
prumery = np.array(prumery)
ax.hist(prumery, bins=30, density=True, alpha=0.7, color='steelblue', edgecolor='black')
if n_hodu >= 5:
# Teoretické normální rozdělení
mu_teor = 3.5 # E[kostka]
var_kostka = 35/12 # Var[kostka]
sigma_teor = np.sqrt(var_kostka / n_hodu) # Var[průměr] = Var/n
x = np.linspace(1, 6, 100)
ax.plot(x, norm_pdf(x, mu_teor, sigma_teor), 'r-', lw=2, label='Teorie')
ax.set_title(f'Průměr z {n_hodu} hodů')
ax.set_xlabel('Průměr')
ax.set_ylabel('Hustota')
ax.grid(True, alpha=0.3)
plt.suptitle('Centrální limitní věta: Průměr hodů kostkou', fontsize=14)
plt.tight_layout()
plt.show()
```
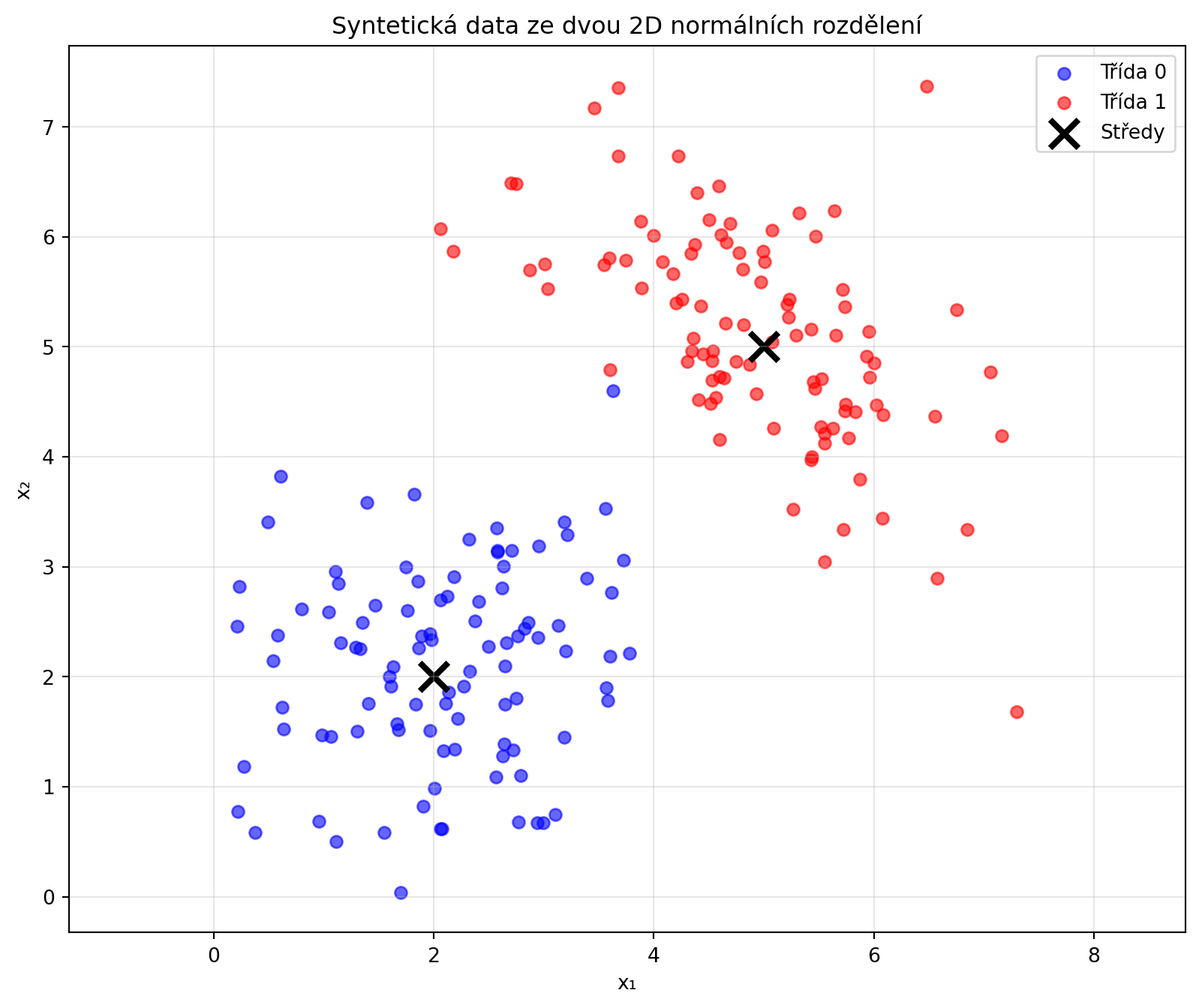
### Příklad 5: Generování syntetických dat
**Zadání**: Vygenerujte syntetická data pro klasifikaci ze dvou 2D normálních rozdělení.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
# Třída 0
mu0 = [2, 2]
sigma0 = [[1, 0.3], [0.3, 1]]
X0 = np.random.multivariate_normal(mu0, sigma0, 100)
# Třída 1
mu1 = [5, 5]
sigma1 = [[1, -0.5], [-0.5, 1]]
X1 = np.random.multivariate_normal(mu1, sigma1, 100)
plt.figure(figsize=(10, 8))
plt.scatter(X0[:, 0], X0[:, 1], c='blue', alpha=0.6, label='Třída 0')
plt.scatter(X1[:, 0], X1[:, 1], c='red', alpha=0.6, label='Třída 1')
plt.scatter([mu0[0], mu1[0]], [mu0[1], mu1[1]], c='black', s=200, marker='x', linewidths=3, label='Středy')
plt.xlabel('x₁')
plt.ylabel('x₂')
plt.title('Syntetická data ze dvou 2D normálních rozdělení')
plt.legend()
plt.axis('equal')
plt.grid(True, alpha=0.3)
plt.show()
# Kombinace do datasetu
X = np.vstack([X0, X1])
y = np.array([0]*100 + [1]*100)
print(f"Dataset: {X.shape[0]} vzorků, {X.shape[1]} features")
print(f"Třídy: {np.bincount(y)}")
```
## Python v praxi: Práce s normálním rozdělením
```{python}
import numpy as np
# Práce s normálním rozdělením pomocí vlastních funkcí
mu, sigma = 50, 10
print("Práce s normálním rozdělením:")
print(f" pdf(x) - hustota: f(50) = {norm_pdf(50, mu, sigma):.4f}")
print(f" cdf(x) - distr. funkce: F(60) = {norm_cdf(60, mu, sigma):.4f}")
print(f" ppf(p) - kvantil: Q(0.95) = {norm_ppf(0.95, mu, sigma):.2f}")
print(f" rvs(n) - vzorky: {np.random.normal(mu, sigma, 5)}")
print(f" mean() - střední hodnota: {mu}")
print(f" var() - rozptyl: {sigma**2}")
print(f" std() - směr. odchylka: {sigma}")
# Intervalové odhady
print(f"\n90% interval: [{norm_ppf(0.05, mu, sigma):.2f}, {norm_ppf(0.95, mu, sigma):.2f}]")
print(f"95% interval: [{norm_ppf(0.025, mu, sigma):.2f}, {norm_ppf(0.975, mu, sigma):.2f}]")
```
## Cvičení
::: {.callout-note icon=false}
## Cvičení 1: Výpočty
Výška mužů má normální rozdělení s μ=178 cm a σ=7 cm.
a) Jaká je pravděpodobnost, že náhodný muž je vyšší než 190 cm?
b) Jakou výšku má nejnižších 10% mužů?
c) Jaká je pravděpodobnost, že výška je mezi 170 a 185 cm?
:::
::: {.callout-note icon=false}
## Cvičení 2: Standardizace
Skóre testu má μ=75 a σ=12. Student dostal 90 bodů.
a) Jaké je jeho z-skóre?
b) Kolik procent studentů dosáhlo horšího výsledku?
:::
::: {.callout-note icon=false}
## Cvičení 3: Inicializace
Implementujte LeCun inicializaci vah: $\sigma = \sqrt{1/n_{in}}$. Porovnejte s Xavier a He inicializací pro vrstvu 1000→500.
:::
::: {.callout-note icon=false}
## Cvičení 4: CLV
Házíte mincí 1000×. Použijte CLV k odhadu pravděpodobnosti, že počet pannen je mezi 480 a 520.
:::
::: {.callout-note icon=false}
## Cvičení 5: Vícerozměrné rozdělení
Vygenerujte 1000 vzorků z 3D normálního rozdělení a vizualizujte projekce do 2D.
:::
::: {.callout-note icon=false}
## Cvičení 6: Kvalita aproximace
Pro různé hodnoty n simulujte průměr z n hodů kostkou a měřte, jak dobře odpovídá normálnímu rozdělení (např. pomocí Q-Q plotu).
:::
## Shrnutí
::: {.callout-tip}
## Co jsme se naučili
1. **Normální rozdělení** $\mathcal{N}(\mu, \sigma^2)$ má charakteristický "zvonový" tvar
2. **Standardní normální** $\mathcal{N}(0, 1)$ je speciální případ s μ=0, σ=1
3. **Z-skóre** převádí libovolné normální na standardní: $Z = \frac{X-\mu}{\sigma}$
4. **Pravidlo 68-95-99.7** udává pravděpodobnosti v intervalech ±1σ, ±2σ, ±3σ
5. **Centrální limitní věta** vysvětluje všudypřítomnost normálního rozdělení
6. **Inicializace vah** v neuronových sítích používá normální rozdělení (Xavier, He)
7. **Vícerozměrné normální** rozdělení je definováno vektorem středů a kovarianční maticí
:::
::: {.callout-important}
## Klíčové pojmy
- **Hustota**: $f(x) = \frac{1}{\sigma\sqrt{2\pi}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$
- **Standardizace**: $Z = \frac{X - \mu}{\sigma}$
- **Pravidlo 68-95-99.7**: Procenta hodnot v intervalech kolem μ
- **CLV**: Součet/průměr konverguje k normálnímu rozdělení
- **Kovarianční matice**: Popisuje vztahy mezi proměnnými
:::
V další kapitole se podíváme na entropii a informaci - koncept, který je klíčový pro pochopení loss funkcí v klasifikaci a měření kvality jazykových modelů.