# Gradient Descent {#sec-gradient-descent}
## Motivace: Jak sestoupit do údolí?
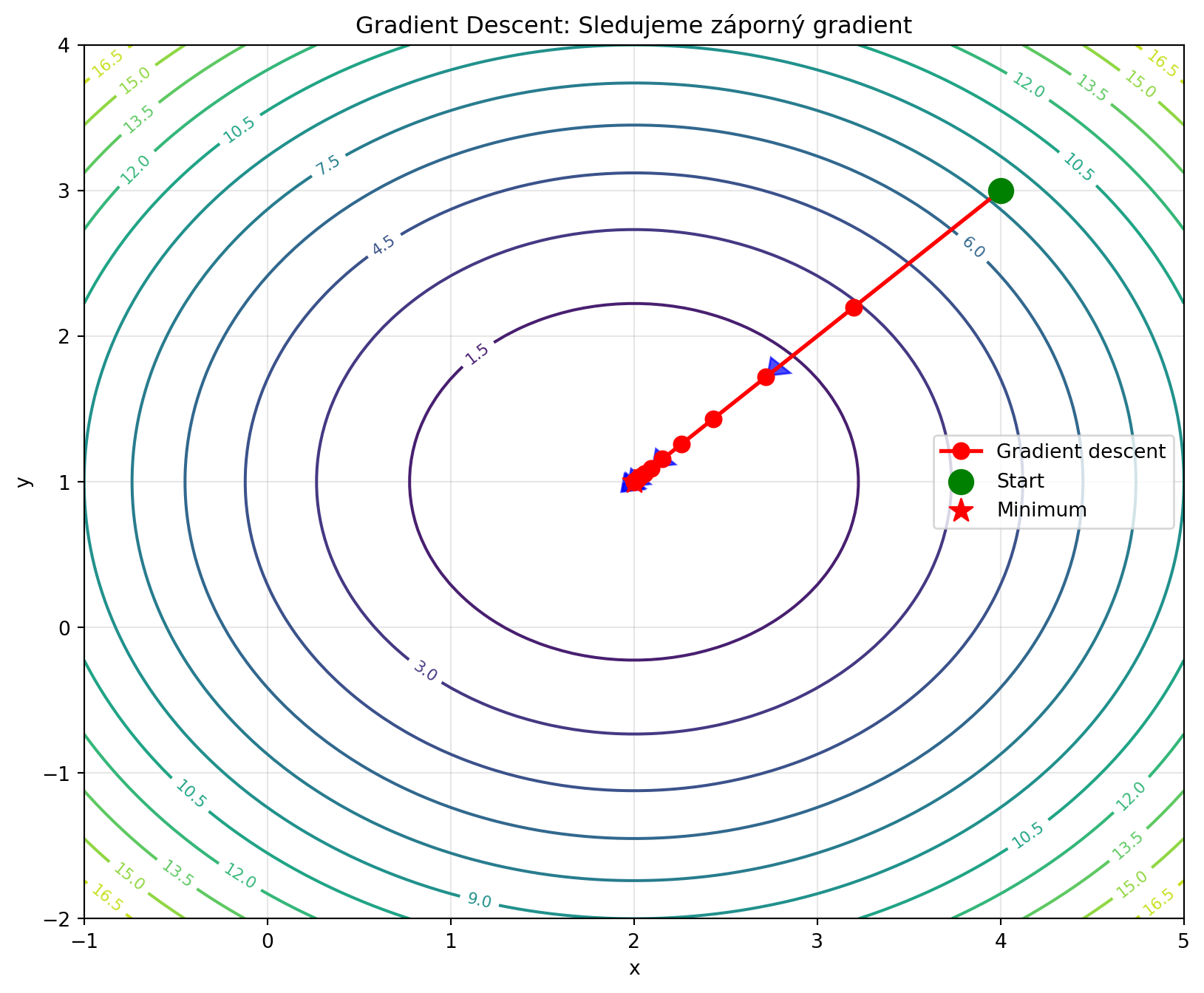
Představte si, že stojíte na kopci v husté mlze a chcete se dostat do údolí. Nevidíte daleko, ale můžete cítit sklon půdy pod nohama. Nejrozumnější strategie? **Jděte směrem, kde to nejvíce klesá.**
Přesně toto dělá **gradient descent** (sestup po gradientu):
1. Spočítej gradient (směr největšího růstu)
2. Udělej krok **opačným směrem** (směr největšího poklesu)
3. Opakuj, dokud nedosáhneš minima
```{python}
import numpy as np
import matplotlib.pyplot as plt
# Vizualizace principu
def loss_function(x, y):
return (x - 2)**2 + (y - 1)**2
x = np.linspace(-1, 5, 100)
y = np.linspace(-2, 4, 100)
X, Y = np.meshgrid(x, y)
Z = loss_function(X, Y)
# Simulace gradient descent
path = [(4, 3)]
lr = 0.2
for _ in range(15):
x_curr, y_curr = path[-1]
# Gradient
grad_x = 2 * (x_curr - 2)
grad_y = 2 * (y_curr - 1)
# Update
x_new = x_curr - lr * grad_x
y_new = y_curr - lr * grad_y
path.append((x_new, y_new))
path = np.array(path)
plt.figure(figsize=(10, 8))
contour = plt.contour(X, Y, Z, levels=15, cmap='viridis')
plt.clabel(contour, inline=True, fontsize=8)
# Cesta
plt.plot(path[:, 0], path[:, 1], 'ro-', markersize=8, lw=2, label='Gradient descent')
plt.scatter([path[0, 0]], [path[0, 1]], color='green', s=150, zorder=5, label='Start')
plt.scatter([2], [1], color='red', s=150, marker='*', zorder=5, label='Minimum')
# Šipky gradientu
for i in range(0, len(path)-1, 3):
x_curr, y_curr = path[i]
grad_x = 2 * (x_curr - 2)
grad_y = 2 * (y_curr - 1)
plt.arrow(x_curr, y_curr, -0.3*grad_x, -0.3*grad_y,
head_width=0.15, head_length=0.1, fc='blue', ec='blue', alpha=0.7)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Gradient Descent: Sledujeme záporný gradient')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
## Algoritmus Gradient Descent
::: {.callout-note}
## Algoritmus: Gradient Descent
**Vstup**: Počáteční bod $\mathbf{w}_0$, learning rate $\eta$, počet iterací $T$
**Opakuj** pro $t = 0, 1, \ldots, T-1$:
$$\mathbf{w}_{t+1} = \mathbf{w}_t - \eta \nabla f(\mathbf{w}_t)$$
**Výstup**: $\mathbf{w}_T$
:::
Klíčové komponenty:
- $\nabla f(\mathbf{w})$ = gradient loss funkce
- $\eta$ = learning rate (krok učení)
- $-\nabla f$ = směr největšího poklesu
```{python}
import numpy as np
def gradient_descent(grad_f, w0, learning_rate=0.1, n_iterations=100):
"""
Základní gradient descent.
Args:
grad_f: Funkce počítající gradient
w0: Počáteční parametry
learning_rate: Velikost kroku
n_iterations: Počet iterací
Returns:
Historie parametrů
"""
w = np.array(w0, dtype=float)
history = [w.copy()]
for _ in range(n_iterations):
grad = grad_f(w)
w = w - learning_rate * grad
history.append(w.copy())
return np.array(history)
# Příklad: f(w) = (w[0] - 3)^2 + (w[1] + 1)^2
def grad_f(w):
return np.array([2 * (w[0] - 3), 2 * (w[1] + 1)])
history = gradient_descent(grad_f, w0=[0, 0], learning_rate=0.1, n_iterations=50)
print(f"Start: {history[0]}")
print(f"Po 10 iteracích: {history[10]}")
print(f"Po 50 iteracích: {history[-1]}")
print(f"Optimum: [3, -1]")
```
## Learning Rate: Klíčový hyperparametr
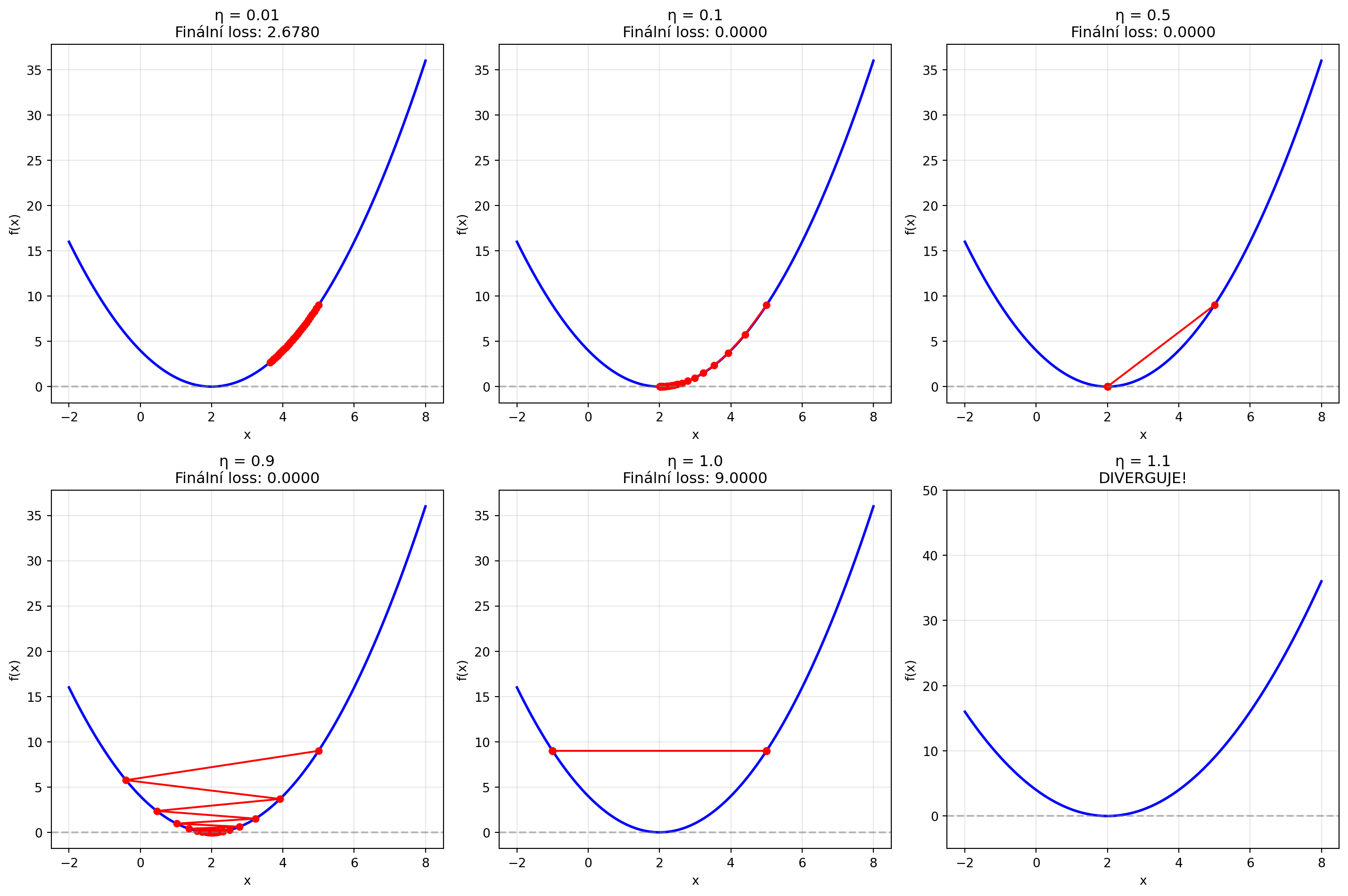
Learning rate ($\eta$) je nejdůležitější hyperparametr gradient descent:
- **Příliš malý** → pomalá konvergence
- **Příliš velký** → oscilace nebo divergence
- **Správný** → rychlá a stabilní konvergence
```{python}
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return (x - 2)**2
def grad_f(x):
return 2 * (x - 2)
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
learning_rates = [0.01, 0.1, 0.5, 0.9, 1.0, 1.1]
for ax, lr in zip(axes.flatten(), learning_rates):
x = 5.0
path = [x]
for _ in range(30):
x = x - lr * grad_f(x)
path.append(x)
if abs(x) > 100:
break
path = np.array(path)
# Funkce
x_range = np.linspace(-2, 8, 100)
ax.plot(x_range, f(x_range), 'b-', lw=2)
# Path (pokud neexplodovala)
if np.max(np.abs(path)) < 50:
ax.plot(path, f(path), 'ro-', markersize=5)
final_loss = f(path[-1])
ax.set_title(f'η = {lr}\nFinální loss: {final_loss:.4f}')
else:
ax.set_title(f'η = {lr}\nDIVERGUJE!')
ax.set_ylim(-5, 50)
ax.set_xlabel('x')
ax.set_ylabel('f(x)')
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='gray', linestyle='--', alpha=0.5)
plt.tight_layout()
plt.show()
```
### Teoretický pohled na learning rate
Pro konvexní funkce s Lipschitzovsky spojitým gradientem existuje optimální learning rate:
```{python}
# Konvergence jako funkce learning rate
import numpy as np
import matplotlib.pyplot as plt
def analyze_convergence(lr, n_steps=50, x0=5.0):
x = x0
losses = [f(x)]
for _ in range(n_steps):
x = x - lr * grad_f(x)
losses.append(f(x))
return losses
lrs = np.linspace(0.01, 1.05, 50)
final_losses = []
for lr in lrs:
try:
losses = analyze_convergence(lr)
if np.isnan(losses[-1]) or losses[-1] > 1000:
final_losses.append(np.nan)
else:
final_losses.append(losses[-1])
except:
final_losses.append(np.nan)
plt.figure(figsize=(10, 5))
plt.semilogy(lrs, final_losses, 'b.-')
plt.axvline(x=1.0, color='red', linestyle='--', label='Hranice stability (η=1)')
plt.xlabel('Learning rate η')
plt.ylabel('Finální loss (log scale)')
plt.title('Vliv learning rate na konvergenci')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
print("Pro f(x) = (x-2)² je Lipschitzova konstanta L = 2")
print("Teoreticky: η < 2/L = 1 pro konvergenci")
```
## Varianty Gradient Descent
### 1. Batch Gradient Descent
Používá **celý dataset** pro výpočet gradientu:
$$\nabla f(\mathbf{w}) = \frac{1}{N} \sum_{i=1}^N \nabla f_i(\mathbf{w})$$
```{python}
import numpy as np
np.random.seed(42)
# Generování dat pro lineární regresi
N = 100
X = np.random.randn(N, 1)
y = 2 * X.squeeze() + 1 + 0.5 * np.random.randn(N)
def compute_gradient_batch(w, b, X, y):
"""Gradient na celém datasetu."""
predictions = X.squeeze() * w + b
errors = predictions - y
dw = 2 * np.mean(errors * X.squeeze())
db = 2 * np.mean(errors)
return dw, db
def mse_loss(w, b, X, y):
predictions = X.squeeze() * w + b
return np.mean((predictions - y)**2)
# Batch gradient descent
w, b = 0.0, 0.0
lr = 0.1
losses_batch = []
for _ in range(100):
losses_batch.append(mse_loss(w, b, X, y))
dw, db = compute_gradient_batch(w, b, X, y)
w -= lr * dw
b -= lr * db
print(f"Batch GD - Naučené parametry: w = {w:.4f}, b = {b:.4f}")
print(f"Skutečné parametry: w = 2.0, b = 1.0")
```
### 2. Stochastic Gradient Descent (SGD)
Používá **jeden vzorek** pro výpočet gradientu:
```{python}
# Stochastic gradient descent
import numpy as np
w, b = 0.0, 0.0
lr = 0.01
losses_sgd = []
X_flat = X.squeeze() # Převod na 1D pole
for epoch in range(100):
epoch_loss = mse_loss(w, b, X, y)
losses_sgd.append(epoch_loss)
# Náhodné pořadí vzorků
indices = np.random.permutation(N)
for i in indices:
xi = X_flat[i]
yi = y[i]
prediction = xi * w + b
error = prediction - yi
# Gradient z jednoho vzorku
dw = 2 * error * xi
db = 2 * error
w -= lr * dw
b -= lr * db
print(f"SGD - Naučené parametry: w = {w:.4f}, b = {b:.4f}")
```
### 3. Mini-batch Gradient Descent
Kompromis - používá **malou skupinu vzorků** (batch):
```{python}
# Mini-batch gradient descent
import numpy as np
import matplotlib.pyplot as plt
w, b = 0.0, 0.0
lr = 0.05
batch_size = 16
losses_minibatch = []
for epoch in range(100):
epoch_loss = mse_loss(w, b, X, y)
losses_minibatch.append(epoch_loss)
# Náhodné pořadí
indices = np.random.permutation(N)
for start in range(0, N, batch_size):
batch_indices = indices[start:start + batch_size]
X_batch = X[batch_indices]
y_batch = y[batch_indices]
dw, db = compute_gradient_batch(w, b, X_batch, y_batch)
w -= lr * dw
b -= lr * db
print(f"Mini-batch GD - Naučené parametry: w = {w:.4f}, b = {b:.4f}")
# Porovnání
plt.figure(figsize=(12, 5))
plt.plot(losses_batch, 'b-', label='Batch GD', lw=2)
plt.plot(losses_sgd, 'r-', label='SGD', alpha=0.7)
plt.plot(losses_minibatch, 'g-', label='Mini-batch GD', lw=2)
plt.xlabel('Epocha')
plt.ylabel('Loss')
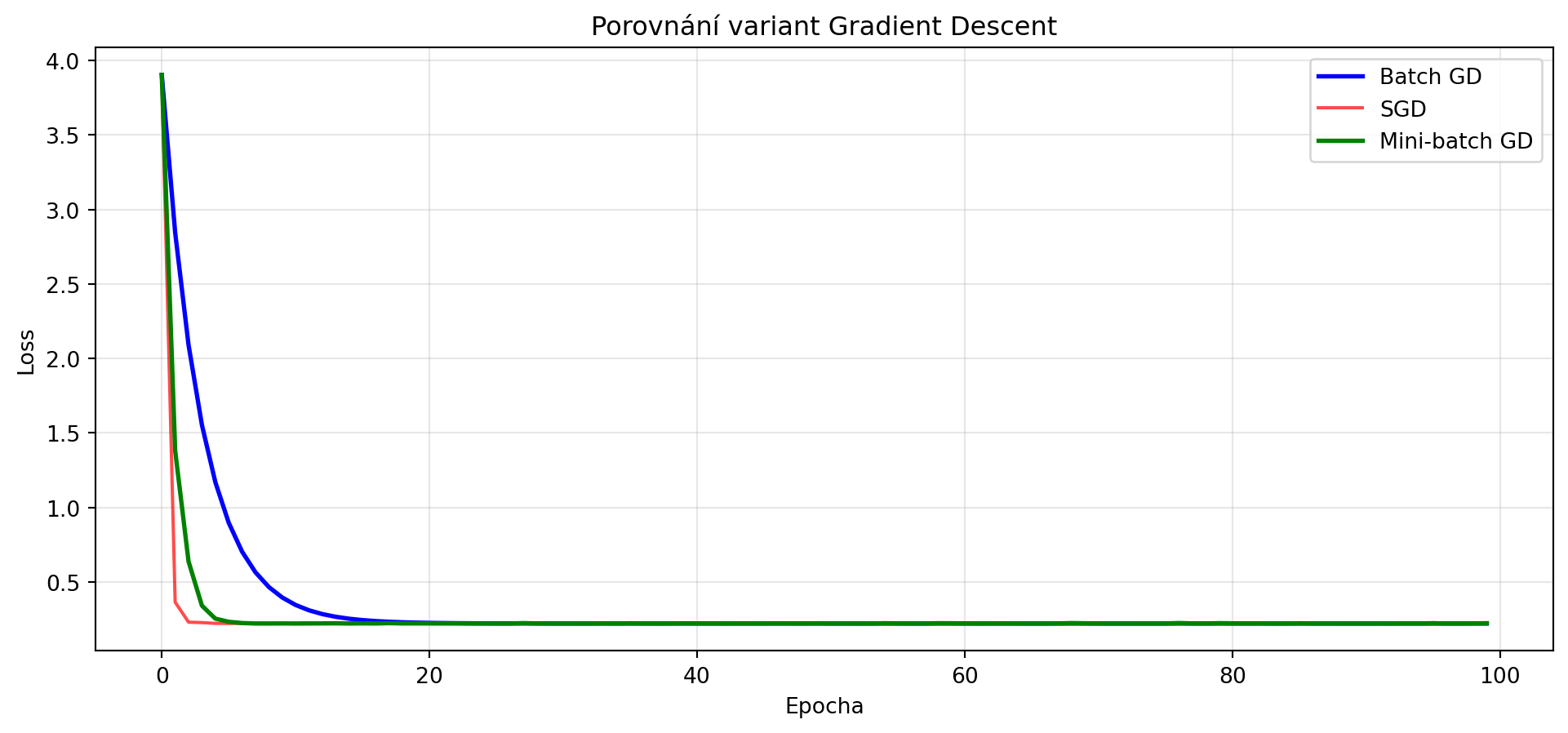
plt.title('Porovnání variant Gradient Descent')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
### Porovnání variant
```{python}
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
varianta = ['Batch GD', 'SGD', 'Mini-batch GD']
vyhody = [
'• Stabilní konvergence\n• Přesný gradient\n• Předvídatelné chování',
'• Rychlé iterace\n• Může uniknout lok. minimům\n• Malá paměť',
'• Kompromis\n• Paralelizace na GPU\n• Prakticky nejpoužívanější'
]
nevyhody = [
'• Pomalé pro velká data\n• Vysoká paměť\n• Může uvíznout v lok. min.',
'• Šumný gradient\n• Nestabilní konvergence\n• Těžší ladění',
'• Výběr batch size\n• Stále nějaký šum',
]
for ax, var, vyh, nev in zip(axes, varianta, vyhody, nevyhody):
ax.text(0.5, 0.9, var, transform=ax.transAxes, fontsize=16,
fontweight='bold', ha='center', va='top')
ax.text(0.5, 0.65, 'Výhody:', transform=ax.transAxes, fontsize=12,
color='green', ha='center', va='top', fontweight='bold')
ax.text(0.5, 0.55, vyh, transform=ax.transAxes, fontsize=10,
ha='center', va='top')
ax.text(0.5, 0.25, 'Nevýhody:', transform=ax.transAxes, fontsize=12,
color='red', ha='center', va='top', fontweight='bold')
ax.text(0.5, 0.15, nev, transform=ax.transAxes, fontsize=10,
ha='center', va='top')
ax.axis('off')
plt.tight_layout()
plt.show()
```
## Problémy Gradient Descent
### 1. Volba learning rate
```{python}
# Demonstrace problému s konstantním learning rate
import numpy as np
import matplotlib.pyplot as plt
def rosenbrock(x, y):
"""Rosenbrockova funkce - klasický test pro optimalizátory."""
return (1 - x)**2 + 100 * (y - x**2)**2
def grad_rosenbrock(pos):
x, y = pos
dx = -2 * (1 - x) + 200 * (y - x**2) * (-2 * x)
dy = 200 * (y - x**2)
return np.array([dx, dy])
# Různé learning rates
lrs = [0.0001, 0.001, 0.005]
paths = []
for lr in lrs:
pos = np.array([-1.0, 1.0])
path = [pos.copy()]
for _ in range(1000):
grad = grad_rosenbrock(pos)
pos = pos - lr * grad
path.append(pos.copy())
paths.append(np.array(path))
# Vizualizace
x = np.linspace(-2, 2, 100)
y = np.linspace(-1, 3, 100)
X, Y = np.meshgrid(x, y)
Z = rosenbrock(X, Y)
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
for ax, path, lr in zip(axes, paths, lrs):
ax.contour(X, Y, Z, levels=np.logspace(-1, 3, 20), cmap='viridis')
ax.plot(path[:, 0], path[:, 1], 'r.-', markersize=2, alpha=0.7)
ax.scatter([1], [1], color='green', s=100, marker='*', zorder=5)
ax.set_title(f'lr = {lr}\nFinální: ({path[-1, 0]:.3f}, {path[-1, 1]:.3f})')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(-2, 2)
ax.set_ylim(-1, 3)
plt.tight_layout()
plt.show()
```
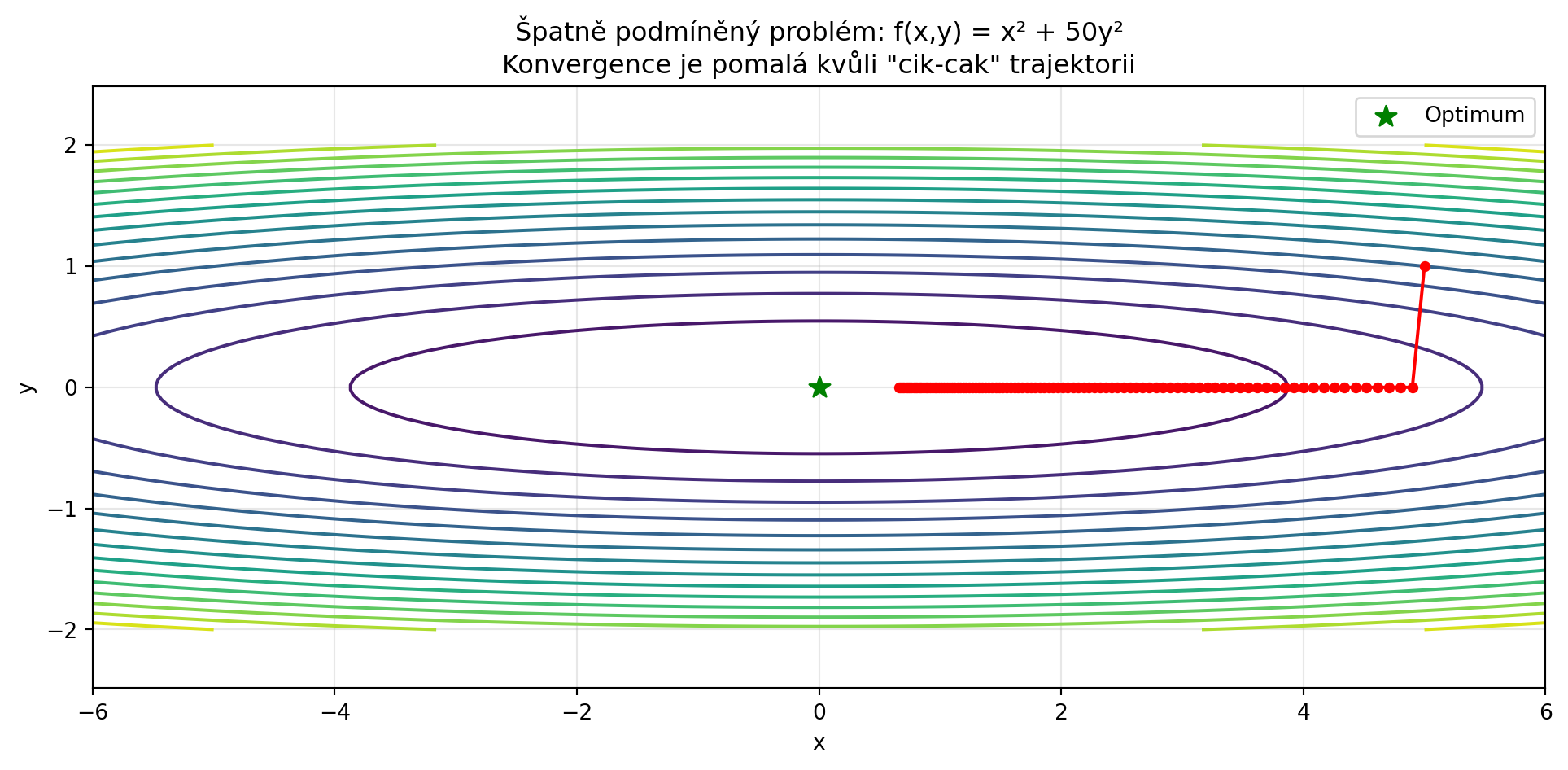
### 2. Špatně podmíněné problémy
Když má loss různou "strmost" v různých směrech:
```{python}
import numpy as np
import matplotlib.pyplot as plt
def ill_conditioned(x, y):
"""Špatně podmíněná funkce."""
return x**2 + 50 * y**2
def grad_ill_conditioned(pos):
return np.array([2 * pos[0], 100 * pos[1]])
# Gradient descent
pos = np.array([5.0, 1.0])
lr = 0.01
path = [pos.copy()]
for _ in range(100):
grad = grad_ill_conditioned(pos)
pos = pos - lr * grad
path.append(pos.copy())
path = np.array(path)
# Vizualizace
x = np.linspace(-6, 6, 100)
y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x, y)
Z = ill_conditioned(X, Y)
plt.figure(figsize=(12, 5))
plt.contour(X, Y, Z, levels=20, cmap='viridis')
plt.plot(path[:, 0], path[:, 1], 'ro-', markersize=4)
plt.scatter([0], [0], color='green', s=100, marker='*', zorder=5, label='Optimum')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Špatně podmíněný problém: f(x,y) = x² + 50y²\nKonvergence je pomalá kvůli "cik-cak" trajektorii')
plt.legend()
plt.axis('equal')
plt.grid(True, alpha=0.3)
plt.show()
```
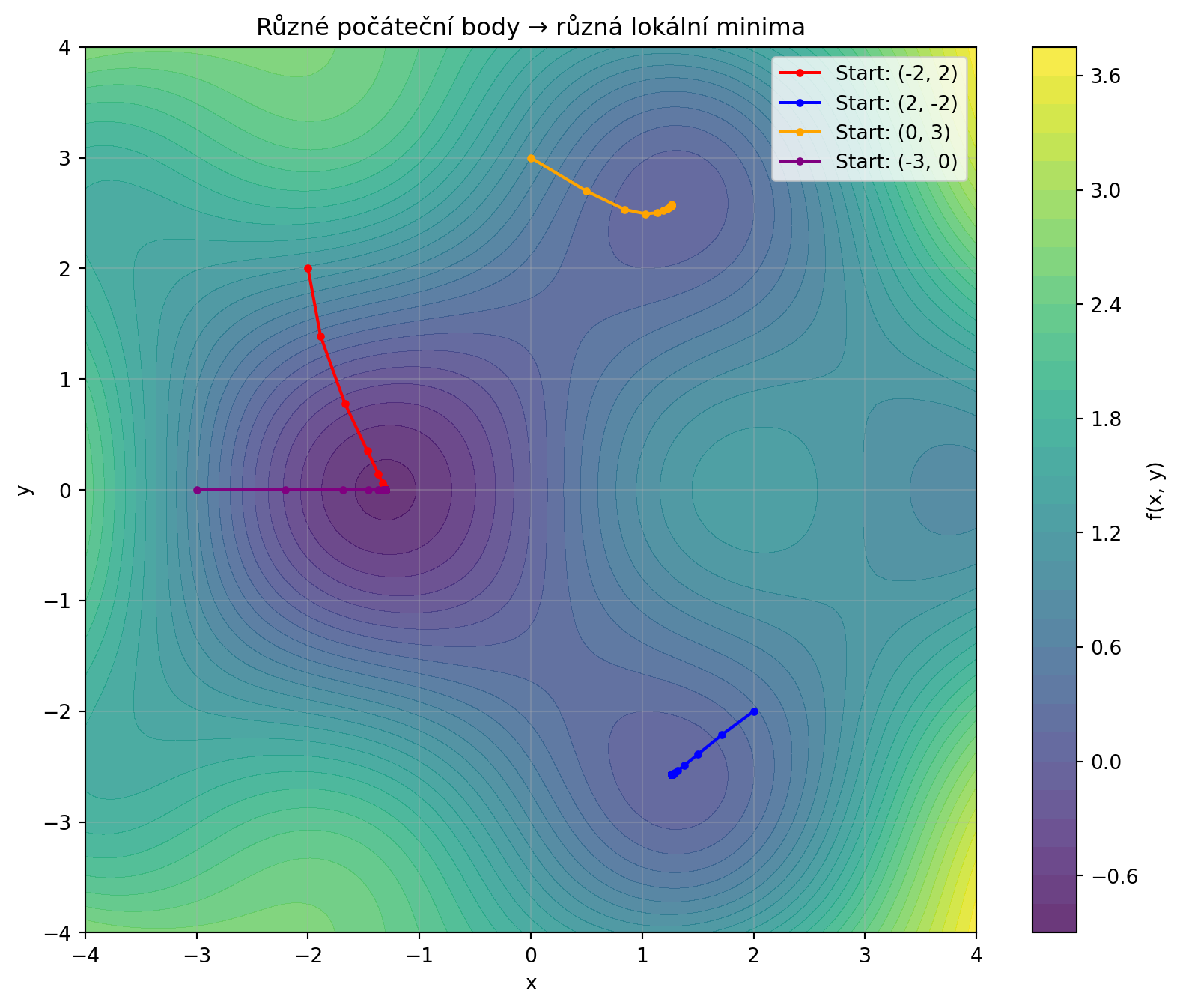
### 3. Lokální minima a sedlové body
```{python}
import numpy as np
import matplotlib.pyplot as plt
def multi_minima(x, y):
return np.sin(x) * np.cos(y) + 0.1 * (x**2 + y**2)
def grad_multi_minima(pos):
x, y = pos
dx = np.cos(x) * np.cos(y) + 0.2 * x
dy = -np.sin(x) * np.sin(y) + 0.2 * y
return np.array([dx, dy])
# Různé počáteční body
starts = [(-2, 2), (2, -2), (0, 3), (-3, 0)]
paths = []
for start in starts:
pos = np.array(start, dtype=float)
path = [pos.copy()]
for _ in range(100):
grad = grad_multi_minima(pos)
pos = pos - 0.5 * grad
path.append(pos.copy())
paths.append(np.array(path))
# Vizualizace
x = np.linspace(-4, 4, 100)
y = np.linspace(-4, 4, 100)
X, Y = np.meshgrid(x, y)
Z = multi_minima(X, Y)
plt.figure(figsize=(10, 8))
plt.contourf(X, Y, Z, levels=30, cmap='viridis', alpha=0.8)
plt.colorbar(label='f(x, y)')
colors = ['red', 'blue', 'orange', 'purple']
for path, color, start in zip(paths, colors, starts):
plt.plot(path[:, 0], path[:, 1], 'o-', color=color, markersize=3,
label=f'Start: {start}')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Různé počáteční body → různá lokální minima')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
## Gradient Descent v PyTorch
PyTorch automatizuje výpočet gradientů a aktualizaci parametrů:
```{python}
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
# Data
torch.manual_seed(42)
X = torch.randn(100, 1)
y = 2 * X + 1 + 0.3 * torch.randn(100, 1)
# Model
model = nn.Linear(1, 1)
criterion = nn.MSELoss()
# Různé optimizátory
optimizers = {
'SGD': optim.SGD(model.parameters(), lr=0.1),
}
# Reset modelu
model.weight.data.fill_(0)
model.bias.data.fill_(0)
losses = []
for epoch in range(100):
# Forward pass
predictions = model(X)
loss = criterion(predictions, y)
losses.append(loss.item())
# Backward pass
optimizers['SGD'].zero_grad() # Vynulování gradientů
loss.backward() # Výpočet gradientů
optimizers['SGD'].step() # Aktualizace parametrů
print(f"Naučené parametry:")
print(f" w = {model.weight.item():.4f} (skutečné: 2.0)")
print(f" b = {model.bias.item():.4f} (skutečné: 1.0)")
plt.figure(figsize=(10, 4))
plt.plot(losses, 'b-', lw=2)
plt.xlabel('Epocha')
plt.ylabel('MSE Loss')
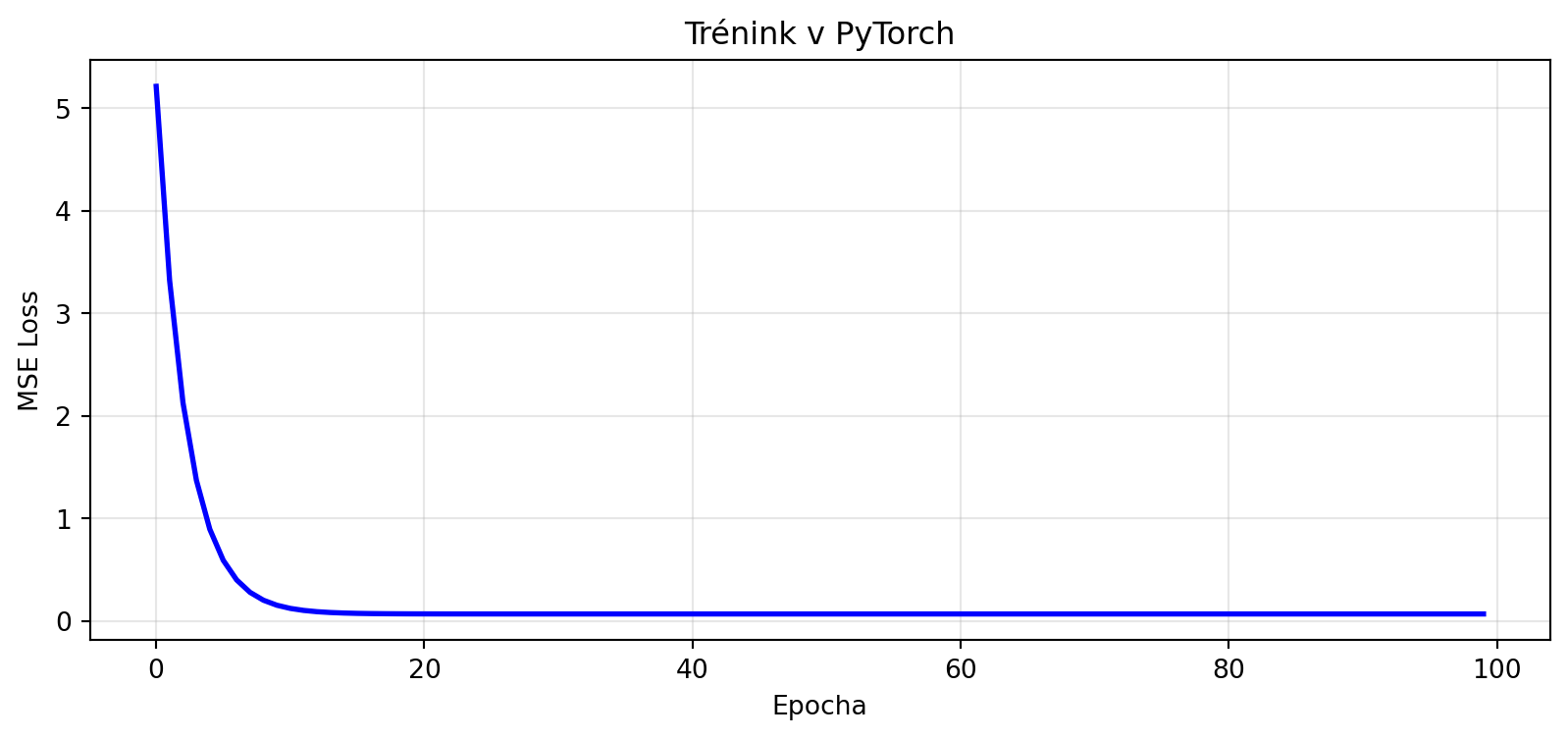
plt.title('Trénink v PyTorch')
plt.grid(True, alpha=0.3)
plt.show()
```
### Kompletní trénovací smyčka
```{python}
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
# Větší dataset
torch.manual_seed(42)
N = 1000
X = torch.randn(N, 2)
y = (X[:, 0] + 2 * X[:, 1] + 0.5 * X[:, 0] * X[:, 1] + 0.3 * torch.randn(N)).unsqueeze(1)
# DataLoader pro mini-batch
dataset = TensorDataset(X, y)
dataloader = DataLoader(dataset, batch_size=32, shuffle=True)
# Model
class SimpleNet(nn.Module):
def __init__(self):
super().__init__()
self.layers = nn.Sequential(
nn.Linear(2, 16),
nn.ReLU(),
nn.Linear(16, 1)
)
def forward(self, x):
return self.layers(x)
model = SimpleNet()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
# Trénink
epoch_losses = []
for epoch in range(50):
epoch_loss = 0
for X_batch, y_batch in dataloader:
# Forward
predictions = model(X_batch)
loss = criterion(predictions, y_batch)
# Backward
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_loss += loss.item()
epoch_losses.append(epoch_loss / len(dataloader))
plt.figure(figsize=(10, 4))
plt.plot(epoch_losses, 'b-', lw=2)
plt.xlabel('Epocha')
plt.ylabel('Průměrná loss')
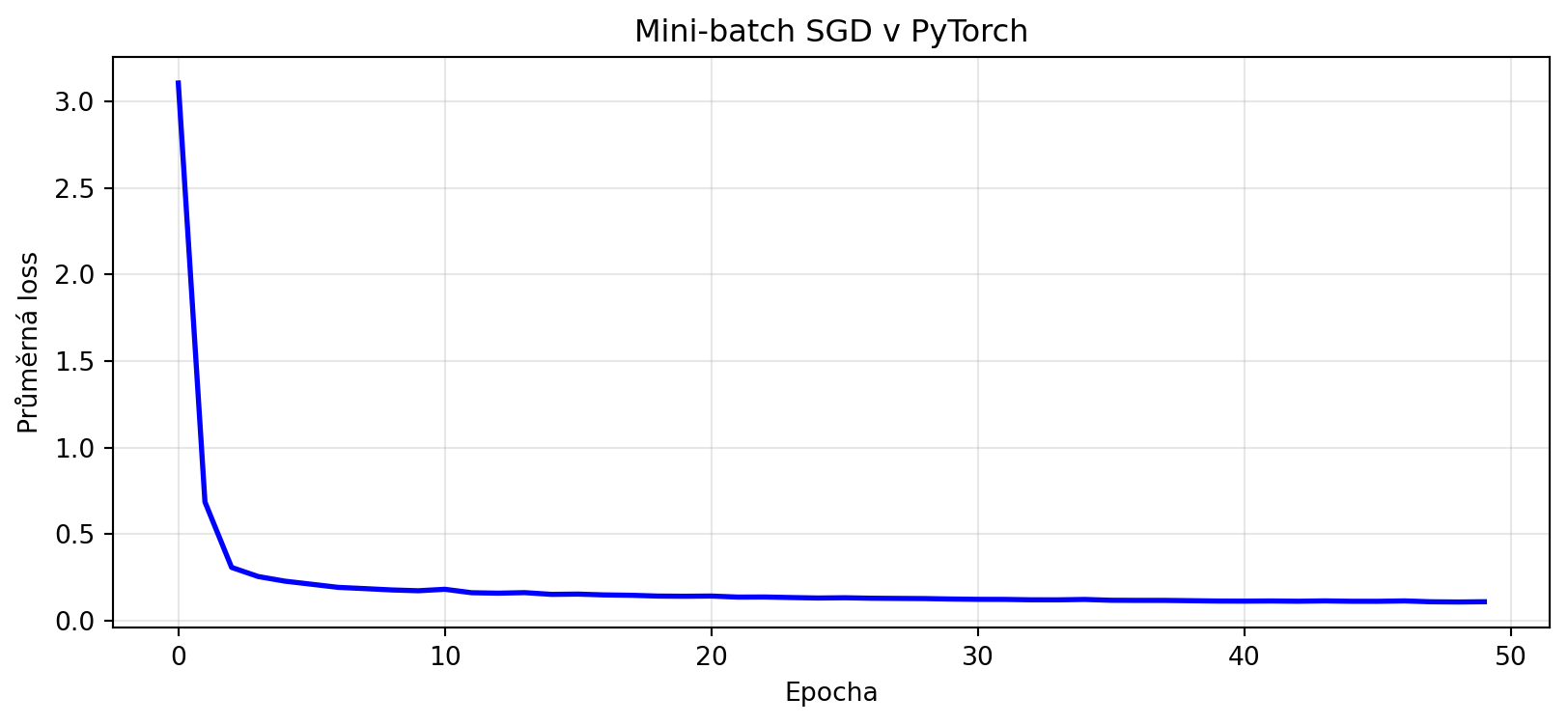
plt.title('Mini-batch SGD v PyTorch')
plt.grid(True, alpha=0.3)
plt.show()
print(f"Finální loss: {epoch_losses[-1]:.4f}")
```
## Řešené příklady
### Příklad 1: Implementace SGD od nuly
**Zadání**: Implementujte SGD pro logistickou regresi.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
# Binární klasifikační data
N = 200
X = np.random.randn(N, 2)
y = (X[:, 0] + X[:, 1] > 0).astype(float)
def sigmoid(z):
return 1 / (1 + np.exp(-np.clip(z, -500, 500)))
def predict(X, w, b):
return sigmoid(X @ w + b)
def cross_entropy_loss(X, y, w, b):
probs = predict(X, w, b)
probs = np.clip(probs, 1e-10, 1 - 1e-10)
return -np.mean(y * np.log(probs) + (1 - y) * np.log(1 - probs))
def compute_gradients(X, y, w, b):
probs = predict(X, w, b)
errors = probs - y
dw = X.T @ errors / len(y)
db = np.mean(errors)
return dw, db
# SGD trénink
w = np.zeros(2)
b = 0.0
lr = 0.5
losses = []
for epoch in range(100):
losses.append(cross_entropy_loss(X, y, w, b))
# Náhodné pořadí
for i in np.random.permutation(N):
xi = X[i:i+1]
yi = y[i:i+1]
dw, db = compute_gradients(xi, yi, w, b)
w -= lr * dw.flatten()
b -= lr * db
# Výsledky
accuracy = np.mean((predict(X, w, b) > 0.5) == y)
print(f"Naučené váhy: w = {w}")
print(f"Naučený bias: b = {b:.4f}")
print(f"Přesnost: {accuracy:.2%}")
# Vizualizace
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# Data a rozhodovací hranice
ax1.scatter(X[y==0, 0], X[y==0, 1], c='blue', alpha=0.5, label='Třída 0')
ax1.scatter(X[y==1, 0], X[y==1, 1], c='red', alpha=0.5, label='Třída 1')
x_line = np.linspace(-3, 3, 100)
y_line = -(w[0] * x_line + b) / w[1]
ax1.plot(x_line, y_line, 'g-', lw=2, label='Rozhodovací hranice')
ax1.set_xlabel('x₁')
ax1.set_ylabel('x₂')
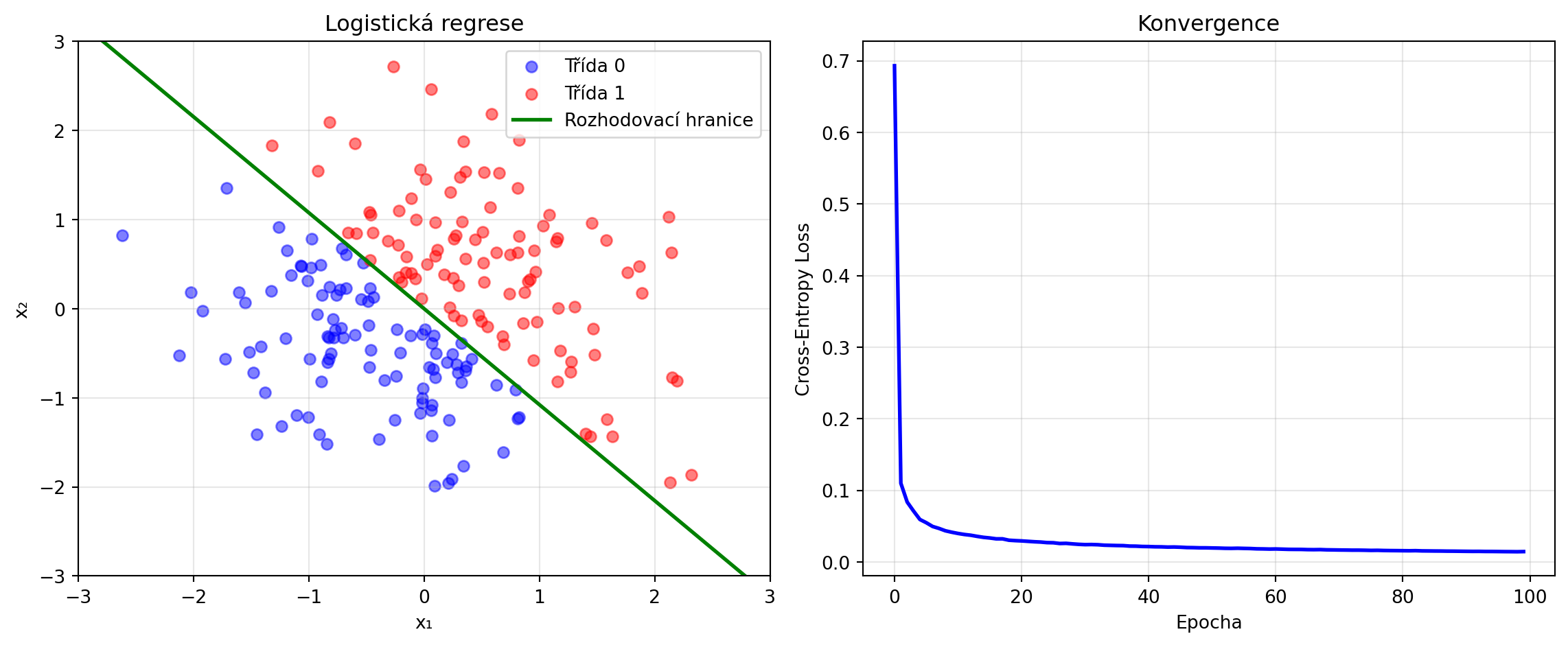
ax1.set_title('Logistická regrese')
ax1.legend()
ax1.set_xlim(-3, 3)
ax1.set_ylim(-3, 3)
ax1.grid(True, alpha=0.3)
# Loss
ax2.plot(losses, 'b-', lw=2)
ax2.set_xlabel('Epocha')
ax2.set_ylabel('Cross-Entropy Loss')
ax2.set_title('Konvergence')
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
### Příklad 2: Vliv batch size
**Zadání**: Porovnejte konvergenci pro různé batch sizes.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
# Data
N = 500
X = np.random.randn(N, 1)
y = 3 * X.squeeze() + 2 + 0.5 * np.random.randn(N)
def train_with_batch_size(batch_size, n_epochs=50):
w, b = 0.0, 0.0
lr = 0.1
losses = []
for epoch in range(n_epochs):
loss = np.mean((X.squeeze() * w + b - y)**2)
losses.append(loss)
indices = np.random.permutation(N)
for start in range(0, N, batch_size):
batch_idx = indices[start:start + batch_size]
X_batch = X[batch_idx].squeeze()
y_batch = y[batch_idx]
pred = X_batch * w + b
error = pred - y_batch
dw = 2 * np.mean(error * X_batch)
db = 2 * np.mean(error)
w -= lr * dw
b -= lr * db
return losses, w, b
batch_sizes = [1, 8, 32, 128, 500]
results = {}
for bs in batch_sizes:
losses, w, b = train_with_batch_size(bs)
results[bs] = losses
# Vizualizace
plt.figure(figsize=(12, 5))
for bs, losses in results.items():
label = f'Batch size = {bs}' + (' (SGD)' if bs == 1 else ' (Full batch)' if bs == 500 else '')
plt.plot(losses, label=label, lw=2)
plt.xlabel('Epocha')
plt.ylabel('MSE Loss')
plt.title('Vliv batch size na konvergenci')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
### Příklad 3: Learning rate scheduling
**Zadání**: Implementujte decay learning rate.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
# Data
X = np.random.randn(100, 1)
y = 2 * X.squeeze() + 1 + 0.3 * np.random.randn(100)
def train_with_schedule(schedule_type='constant', initial_lr=0.5, n_epochs=100):
w, b = 0.0, 0.0
losses = []
lrs = []
for epoch in range(n_epochs):
# Výpočet learning rate podle schedule
if schedule_type == 'constant':
lr = initial_lr
elif schedule_type == 'step':
lr = initial_lr * (0.5 ** (epoch // 30))
elif schedule_type == 'exponential':
lr = initial_lr * (0.95 ** epoch)
elif schedule_type == 'cosine':
lr = initial_lr * 0.5 * (1 + np.cos(np.pi * epoch / n_epochs))
lrs.append(lr)
loss = np.mean((X.squeeze() * w + b - y)**2)
losses.append(loss)
pred = X.squeeze() * w + b
error = pred - y
dw = 2 * np.mean(error * X.squeeze())
db = 2 * np.mean(error)
w -= lr * dw
b -= lr * db
return losses, lrs
schedules = ['constant', 'step', 'exponential', 'cosine']
results = {s: train_with_schedule(s) for s in schedules}
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))
for schedule in schedules:
losses, lrs = results[schedule]
ax1.plot(losses, label=schedule, lw=2)
ax2.plot(lrs, label=schedule, lw=2)
ax1.set_xlabel('Epocha')
ax1.set_ylabel('Loss')
ax1.set_title('Konvergence s různými LR schedules')
ax1.legend()
ax1.grid(True, alpha=0.3)
ax2.set_xlabel('Epocha')
ax2.set_ylabel('Learning rate')
ax2.set_title('Learning rate schedules')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
### Příklad 4: Gradient clipping
**Zadání**: Implementujte gradient clipping pro stabilizaci tréninku.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
def clip_gradient(grad, max_norm=1.0):
"""Ořízne gradient, pokud jeho norma překročí max_norm."""
norm = np.linalg.norm(grad)
if norm > max_norm:
grad = grad * max_norm / norm
return grad
# Demonstrace na "explodujícím" problému
def steep_function(x):
return x**4
def grad_steep(x):
return 4 * x**3
x_no_clip = 5.0
x_with_clip = 5.0
lr = 0.01
history_no_clip = [x_no_clip]
history_with_clip = [x_with_clip]
for _ in range(50):
# Bez clippingu
grad = grad_steep(x_no_clip)
if abs(x_no_clip) < 1000: # Ochrana proti explozi
x_no_clip = x_no_clip - lr * grad
history_no_clip.append(x_no_clip)
# S clippingem
grad = grad_steep(x_with_clip)
grad = clip_gradient(np.array([grad]), max_norm=10.0)[0]
x_with_clip = x_with_clip - lr * grad
history_with_clip.append(x_with_clip)
plt.figure(figsize=(10, 5))
plt.plot(history_no_clip[:30], 'r-', label='Bez clippingu', lw=2)
plt.plot(history_with_clip, 'g-', label='S gradient clipping', lw=2)
plt.xlabel('Iterace')
plt.ylabel('x')
plt.title('Gradient Clipping stabilizuje trénink')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
## Cvičení
::: {.callout-note icon=false}
## Cvičení 1: Implementace
Implementujte mini-batch gradient descent od nuly pro kvadratickou regresi $y = ax^2 + bx + c$.
:::
::: {.callout-note icon=false}
## Cvičení 2: Learning rate finder
Implementujte "learning rate finder" - trénujte model s exponenciálně rostoucím learning rate a sledujte, kde loss začne růst. Toto je dobrý odhad maximálního použitelného learning rate.
:::
::: {.callout-note icon=false}
## Cvičení 3: Warmup
Implementujte "warmup" strategii - začněte s malým learning rate a postupně ho zvyšujte během prvních epoch.
:::
::: {.callout-note icon=false}
## Cvičení 4: Porovnání
Porovnejte konvergenci SGD na Rosenbrockově funkci pro různé počáteční body. Kolik z nich konverguje k globálnímu minimu (1, 1)?
:::
::: {.callout-note icon=false}
## Cvičení 5: PyTorch
Natrénujte jednoduchou neuronovou síť v PyTorch na datasetu MNIST (nebo jiném) pomocí SGD. Experimentujte s learning rate a batch size.
:::
## Shrnutí
::: {.callout-tip}
## Co jsme se naučili
1. **Gradient descent** iterativně sleduje záporný gradient k minimu
2. **Learning rate** je kritický - příliš malý = pomalé, příliš velký = nestabilní
3. **Batch GD** používá celý dataset - stabilní, ale pomalé
4. **SGD** používá jeden vzorek - rychlé, ale šumné
5. **Mini-batch** je praktický kompromis - nejpoužívanější varianta
6. **Problémy**: špatně podmíněné funkce, lokální minima, volba hyperparametrů
7. **PyTorch** automatizuje gradienty a nabízí různé optimizátory
:::
::: {.callout-important}
## Klíčové vzorce
- **Update pravidlo**: $\mathbf{w}_{t+1} = \mathbf{w}_t - \eta \nabla f(\mathbf{w}_t)$
- **Batch gradient**: $\nabla f = \frac{1}{N}\sum_{i=1}^N \nabla f_i$
- **SGD gradient**: $\nabla f \approx \nabla f_i$ pro náhodné $i$
- **Mini-batch**: $\nabla f \approx \frac{1}{B}\sum_{i \in \text{batch}} \nabla f_i$
:::
V další kapitole se podíváme na pokročilé optimalizátory jako Momentum, RMSprop a Adam, které řeší mnoho problémů základního gradient descent.