# Úvod do transformerů {#sec-transformery}
## Motivace: Revoluce v AI
V roce 2017 výzkumníci z Google publikovali článek "Attention Is All You Need" a představili architekturu **Transformer**. Od té doby transformery změnily svět AI:
- **GPT** (OpenAI) - generování textu
- **BERT** (Google) - porozumění jazyku
- **ChatGPT**, **Claude** - konverzační AI
- **DALL-E**, **Stable Diffusion** - generování obrázků
- **AlphaFold** - predikce struktury proteinů
Klíčem k úspěchu transformerů je mechanismus **attention** (pozornost), který umožňuje modelu "zaměřit se" na relevantní části vstupu.
```{python}
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.nn.functional as F
# Vizualizace attention
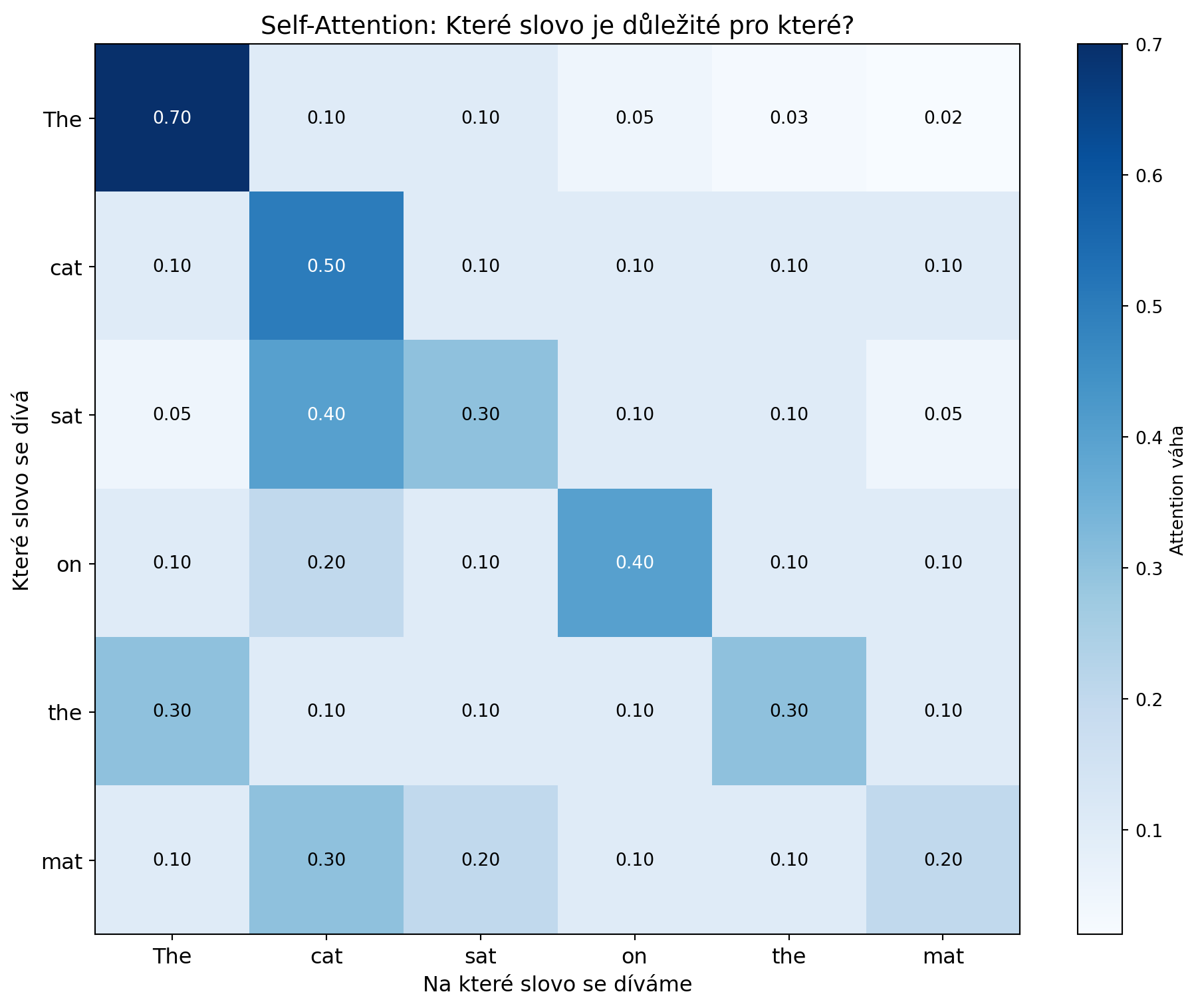
fig, ax = plt.subplots(figsize=(10, 8))
# Příklad věty
words_from = ['The', 'cat', 'sat', 'on', 'the', 'mat']
words_to = words_from.copy()
# Simulované attention váhy (které slovo se dívá na které)
np.random.seed(42)
attention = np.array([
[0.7, 0.1, 0.1, 0.05, 0.03, 0.02], # The
[0.1, 0.5, 0.1, 0.1, 0.1, 0.1], # cat
[0.05, 0.4, 0.3, 0.1, 0.1, 0.05], # sat
[0.1, 0.2, 0.1, 0.4, 0.1, 0.1], # on
[0.3, 0.1, 0.1, 0.1, 0.3, 0.1], # the
[0.1, 0.3, 0.2, 0.1, 0.1, 0.2], # mat
])
# Heatmapa
im = ax.imshow(attention, cmap='Blues', aspect='auto')
ax.set_xticks(range(len(words_to)))
ax.set_yticks(range(len(words_from)))
ax.set_xticklabels(words_to, fontsize=12)
ax.set_yticklabels(words_from, fontsize=12)
ax.set_xlabel('Na které slovo se díváme', fontsize=12)
ax.set_ylabel('Které slovo se dívá', fontsize=12)
ax.set_title('Self-Attention: Které slovo je důležité pro které?', fontsize=14)
# Hodnoty v buňkách
for i in range(len(words_from)):
for j in range(len(words_to)):
text = ax.text(j, i, f'{attention[i, j]:.2f}',
ha='center', va='center', fontsize=10,
color='white' if attention[i, j] > 0.3 else 'black')
plt.colorbar(im, label='Attention váha')
plt.tight_layout()
plt.show()
```
## Co je Attention?
**Attention** mechanismus umožňuje modelu dynamicky vybírat, na které části vstupu se zaměřit při zpracování každé pozice.
::: {.callout-note}
## Intuice: Attention jako vyhledávání
Představte si attention jako systém **Query-Key-Value**:
- **Query (Q)**: "Co hledám?"
- **Key (K)**: "Co nabízím?"
- **Value (V)**: "Jakou informaci mám?"
Výstup = vážený součet Values, kde váhy jsou určeny podobností Query a Keys.
:::
```{python}
import numpy as np
def simple_attention(query, keys, values):
"""
Jednoduchý attention mechanismus.
Args:
query: Co hledáme (d_k,)
keys: Klíče (n, d_k)
values: Hodnoty (n, d_v)
Returns:
Vážený součet values
"""
# Skóre = podobnost query a keys (dot product)
scores = keys @ query
# Váhy = softmax(skóre)
weights = np.exp(scores) / np.sum(np.exp(scores))
# Výstup = vážený součet values
output = values.T @ weights
return output, weights
# Příklad
np.random.seed(42)
d_k, d_v, n = 4, 3, 5
query = np.random.randn(d_k)
keys = np.random.randn(n, d_k)
values = np.random.randn(n, d_v)
output, weights = simple_attention(query, keys, values)
print("Jednoduchý Attention:")
print(f" Query shape: {query.shape}")
print(f" Keys shape: {keys.shape}")
print(f" Values shape: {values.shape}")
print(f" Attention weights: {weights.round(3)}")
print(f" Output shape: {output.shape}")
```
## Scaled Dot-Product Attention
Transformery používají **scaled dot-product attention**:
::: {.callout-note}
## Scaled Dot-Product Attention
$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$$
kde:
- $Q \in \mathbb{R}^{n \times d_k}$ jsou queries
- $K \in \mathbb{R}^{n \times d_k}$ jsou keys
- $V \in \mathbb{R}^{n \times d_v}$ jsou values
- $\sqrt{d_k}$ je škálovací faktor
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
def scaled_dot_product_attention(Q, K, V, mask=None):
"""
Scaled Dot-Product Attention.
Args:
Q: Queries (batch, n, d_k)
K: Keys (batch, n, d_k)
V: Values (batch, n, d_v)
mask: Volitelná maska pro kauzální attention
"""
d_k = Q.shape[-1]
# Skóre - transpozice posledních dvou dimenzí
K_T = np.swapaxes(K, -2, -1) # Transpozice pro NumPy
scores = Q @ K_T / np.sqrt(d_k)
# Aplikace masky (pro dekodér)
if mask is not None:
scores = np.where(mask, scores, -1e9)
# Softmax přes keys
attention_weights = np.exp(scores - np.max(scores, axis=-1, keepdims=True))
attention_weights = attention_weights / np.sum(attention_weights, axis=-1, keepdims=True)
# Vážený součet values
output = attention_weights @ V
return output, attention_weights
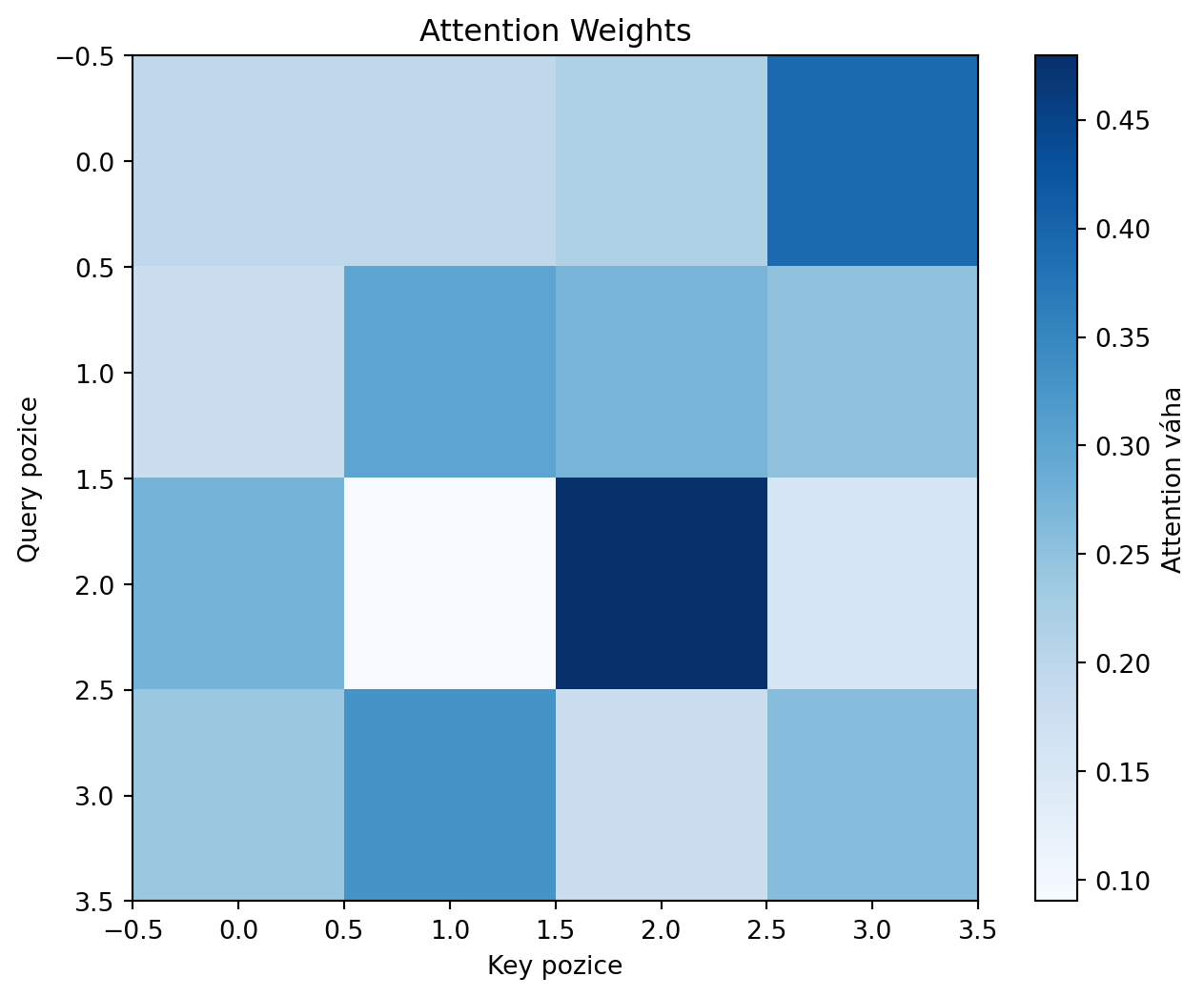
# Příklad s sekvencí
seq_len, d_k, d_v = 4, 8, 8
Q = np.random.randn(1, seq_len, d_k)
K = np.random.randn(1, seq_len, d_k)
V = np.random.randn(1, seq_len, d_v)
output, weights = scaled_dot_product_attention(Q, K, V)
print("Scaled Dot-Product Attention:")
print(f" Vstup Q, K, V: (1, {seq_len}, {d_k})")
print(f" Attention weights: {weights[0].round(2)}")
print(f" Výstup: {output.shape}")
# Vizualizace attention weights
plt.figure(figsize=(8, 6))
plt.imshow(weights[0], cmap='Blues')
plt.colorbar(label='Attention váha')
plt.xlabel('Key pozice')
plt.ylabel('Query pozice')
plt.title('Attention Weights')
plt.show()
```
## Multi-Head Attention
Transformery používají **více attention hlav** paralelně, každá se zaměřuje na jiné aspekty:
::: {.callout-note}
## Multi-Head Attention
$$\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \ldots, \text{head}_h)W^O$$
kde každá hlava:
$$\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)$$
:::
```{python}
import numpy as np
class MultiHeadAttention(nn.Module):
def __init__(self, d_model, n_heads):
super().__init__()
self.n_heads = n_heads
self.d_k = d_model // n_heads
self.W_q = nn.Linear(d_model, d_model)
self.W_k = nn.Linear(d_model, d_model)
self.W_v = nn.Linear(d_model, d_model)
self.W_o = nn.Linear(d_model, d_model)
def forward(self, Q, K, V, mask=None):
batch_size = Q.size(0)
# Lineární projekce a rozdělení na hlavy
Q = self.W_q(Q).view(batch_size, -1, self.n_heads, self.d_k).transpose(1, 2)
K = self.W_k(K).view(batch_size, -1, self.n_heads, self.d_k).transpose(1, 2)
V = self.W_v(V).view(batch_size, -1, self.n_heads, self.d_k).transpose(1, 2)
# Attention
scores = Q @ K.transpose(-2, -1) / np.sqrt(self.d_k)
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
attention = F.softmax(scores, dim=-1)
x = attention @ V
# Spojení hlav
x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.n_heads * self.d_k)
return self.W_o(x), attention
# Test
torch.manual_seed(42)
d_model, n_heads, seq_len = 64, 8, 10
mha = MultiHeadAttention(d_model, n_heads)
x = torch.randn(2, seq_len, d_model)
output, attn = mha(x, x, x)
print("Multi-Head Attention:")
print(f" Vstup: {x.shape}")
print(f" Počet hlav: {n_heads}")
print(f" d_k na hlavu: {d_model // n_heads}")
print(f" Výstup: {output.shape}")
print(f" Attention shape: {attn.shape}")
```
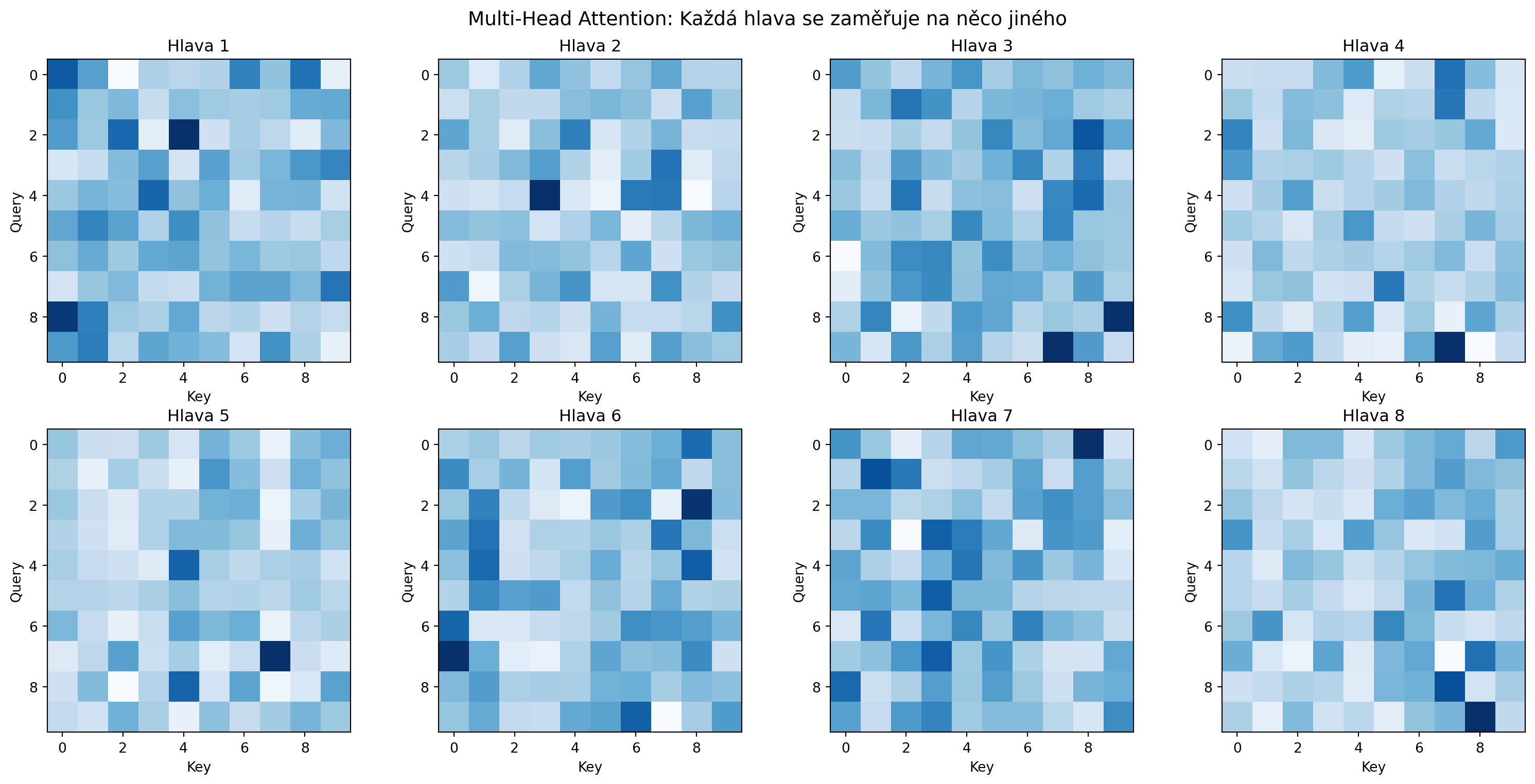
### Vizualizace více hlav
```{python}
# Vizualizace attention pro různé hlavy
import matplotlib.pyplot as plt
fig, axes = plt.subplots(2, 4, figsize=(16, 8))
for i, ax in enumerate(axes.flatten()):
if i < n_heads:
im = ax.imshow(attn[0, i].detach().numpy(), cmap='Blues')
ax.set_title(f'Hlava {i+1}')
ax.set_xlabel('Key')
ax.set_ylabel('Query')
plt.suptitle('Multi-Head Attention: Každá hlava se zaměřuje na něco jiného', fontsize=14)
plt.tight_layout()
plt.show()
```
## Pozicové kódování
Attention je **permutačně invariantní** - nezáleží na pořadí. Pro zachycení pozice přidáváme **positional encoding**:
::: {.callout-note}
## Sinusoidální pozicové kódování
$$PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right)$$
$$PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right)$$
Různé frekvence pro různé dimenze umožňují modelu rozlišovat pozice.
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
def positional_encoding(seq_len, d_model):
"""Generuje sinusoidální pozicové kódování."""
PE = np.zeros((seq_len, d_model))
position = np.arange(seq_len)[:, np.newaxis]
div_term = np.exp(np.arange(0, d_model, 2) * (-np.log(10000.0) / d_model))
PE[:, 0::2] = np.sin(position * div_term)
PE[:, 1::2] = np.cos(position * div_term)
return PE
# Vizualizace
seq_len, d_model = 50, 64
PE = positional_encoding(seq_len, d_model)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))
# Heatmapa
im = ax1.imshow(PE, cmap='RdBu', aspect='auto')
ax1.set_xlabel('Dimenze')
ax1.set_ylabel('Pozice')
ax1.set_title('Pozicové kódování')
plt.colorbar(im, ax=ax1)
# Jednotlivé dimenze
for i in [0, 1, 4, 5, 10, 11]:
ax2.plot(PE[:, i], label=f'dim {i}')
ax2.set_xlabel('Pozice')
ax2.set_ylabel('Hodnota')
ax2.set_title('Pozicové kódování pro vybrané dimenze')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
## Transformer blok
Kompletní Transformer blok obsahuje:
1. **Multi-Head Self-Attention**
2. **Add & Norm** (residual connection + layer normalization)
3. **Feed-Forward Network**
4. **Add & Norm**
```{python}
class TransformerBlock(nn.Module):
def __init__(self, d_model, n_heads, d_ff, dropout=0.1):
super().__init__()
self.attention = MultiHeadAttention(d_model, n_heads)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.ff = nn.Sequential(
nn.Linear(d_model, d_ff),
nn.GELU(),
nn.Linear(d_ff, d_model),
nn.Dropout(dropout)
)
self.dropout = nn.Dropout(dropout)
def forward(self, x, mask=None):
# Self-Attention + Residual
attn_out, _ = self.attention(x, x, x, mask)
x = self.norm1(x + self.dropout(attn_out))
# Feed-Forward + Residual
ff_out = self.ff(x)
x = self.norm2(x + ff_out)
return x
# Test
block = TransformerBlock(d_model=64, n_heads=8, d_ff=256)
x = torch.randn(2, 10, 64)
output = block(x)
print("Transformer Block:")
print(f" Vstup: {x.shape}")
print(f" Výstup: {output.shape}")
```
### Architektura bloku
```{python}
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 12))
# Komponenty
components = [
(0.5, 0.9, 'Input Embeddings', '#3498db'),
(0.5, 0.78, 'Positional Encoding', '#9b59b6'),
(0.5, 0.65, 'Multi-Head\nSelf-Attention', '#2ecc71'),
(0.5, 0.52, 'Add & Norm', '#f39c12'),
(0.5, 0.39, 'Feed-Forward\nNetwork', '#e74c3c'),
(0.5, 0.26, 'Add & Norm', '#f39c12'),
(0.5, 0.13, 'Output', '#3498db'),
]
for x, y, label, color in components:
rect = plt.Rectangle((x-0.15, y-0.05), 0.3, 0.1,
facecolor=color, edgecolor='black', lw=2)
ax.add_patch(rect)
ax.text(x, y, label, ha='center', va='center', fontsize=10, fontweight='bold')
# Šipky
for i in range(len(components) - 1):
y1 = components[i][1] - 0.05
y2 = components[i+1][1] + 0.05
ax.annotate('', xy=(0.5, y2), xytext=(0.5, y1),
arrowprops=dict(arrowstyle='->', color='black', lw=2))
# Residual connections
ax.annotate('', xy=(0.35, 0.57), xytext=(0.35, 0.7),
arrowprops=dict(arrowstyle='->', color='gray', lw=1.5,
connectionstyle='arc3,rad=-0.3'))
ax.annotate('', xy=(0.35, 0.31), xytext=(0.35, 0.44),
arrowprops=dict(arrowstyle='->', color='gray', lw=1.5,
connectionstyle='arc3,rad=-0.3'))
ax.text(0.25, 0.635, 'Residual', fontsize=8, color='gray')
ax.text(0.25, 0.375, 'Residual', fontsize=8, color='gray')
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.axis('off')
ax.set_title('Transformer Block', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.show()
```
## Jednoduchý GPT-style model
Sestavíme jednoduchý dekodérový model typu GPT:
```{python}
class SimpleGPT(nn.Module):
def __init__(self, vocab_size, d_model, n_heads, n_layers, max_len=512):
super().__init__()
self.token_embedding = nn.Embedding(vocab_size, d_model)
self.position_embedding = nn.Embedding(max_len, d_model)
self.blocks = nn.ModuleList([
TransformerBlock(d_model, n_heads, d_model * 4)
for _ in range(n_layers)
])
self.ln_final = nn.LayerNorm(d_model)
self.head = nn.Linear(d_model, vocab_size, bias=False)
def forward(self, idx):
B, T = idx.shape
# Embeddingy
tok_emb = self.token_embedding(idx)
pos_emb = self.position_embedding(torch.arange(T, device=idx.device))
x = tok_emb + pos_emb
# Kauzální maska
mask = torch.tril(torch.ones(T, T)).unsqueeze(0).unsqueeze(0)
# Transformer bloky
for block in self.blocks:
x = block(x)
# Výstup
x = self.ln_final(x)
logits = self.head(x)
return logits
# Test
model = SimpleGPT(vocab_size=1000, d_model=64, n_heads=4, n_layers=2)
idx = torch.randint(0, 1000, (2, 20))
logits = model(idx)
print("Simple GPT:")
print(f" Vstup (token ids): {idx.shape}")
print(f" Výstup (logits): {logits.shape}")
print(f" Počet parametrů: {sum(p.numel() for p in model.parameters()):,}")
```
## Generování textu
```{python}
def generate(model, idx, max_new_tokens, temperature=1.0):
"""Generuje nové tokeny pomocí autoregresivního vzorkování."""
model.eval()
for _ in range(max_new_tokens):
# Predikce dalšího tokenu
with torch.no_grad():
logits = model(idx)
logits = logits[:, -1, :] / temperature
# Vzorkování z distribuce
probs = F.softmax(logits, dim=-1)
next_token = torch.multinomial(probs, num_samples=1)
# Přidání k sekvenci
idx = torch.cat([idx, next_token], dim=1)
return idx
# Generování
torch.manual_seed(42)
start = torch.randint(0, 1000, (1, 5))
generated = generate(model, start, max_new_tokens=10)
print("Generování textu:")
print(f" Počáteční tokeny: {start[0].tolist()}")
print(f" Vygenerované tokeny: {generated[0].tolist()}")
```
## Řešené příklady
### Příklad 1: Ruční výpočet attention
**Zadání**: Pro $Q = [1, 0]$, $K = [[1, 0], [0, 1], [1, 1]]$, $V = [[1], [2], [3]]$ spočítejte attention výstup.
**Řešení**:
```{python}
import numpy as np
Q = np.array([1, 0])
K = np.array([[1, 0], [0, 1], [1, 1]])
V = np.array([[1], [2], [3]])
print("Ruční výpočet Attention:")
print(f"Q = {Q}")
print(f"K = \n{K}")
print(f"V = \n{V}")
# Skóre
scores = K @ Q
print(f"\n1. Skóre = K @ Q = {scores}")
# Scaling
d_k = len(Q)
scaled_scores = scores / np.sqrt(d_k)
print(f"2. Scaled skóre = scores / √d_k = {scaled_scores}")
# Softmax
exp_scores = np.exp(scaled_scores - np.max(scaled_scores))
weights = exp_scores / np.sum(exp_scores)
print(f"3. Attention weights = softmax(scaled) = {weights.round(4)}")
# Výstup
output = V.T @ weights
print(f"4. Výstup = V.T @ weights = {output}")
```
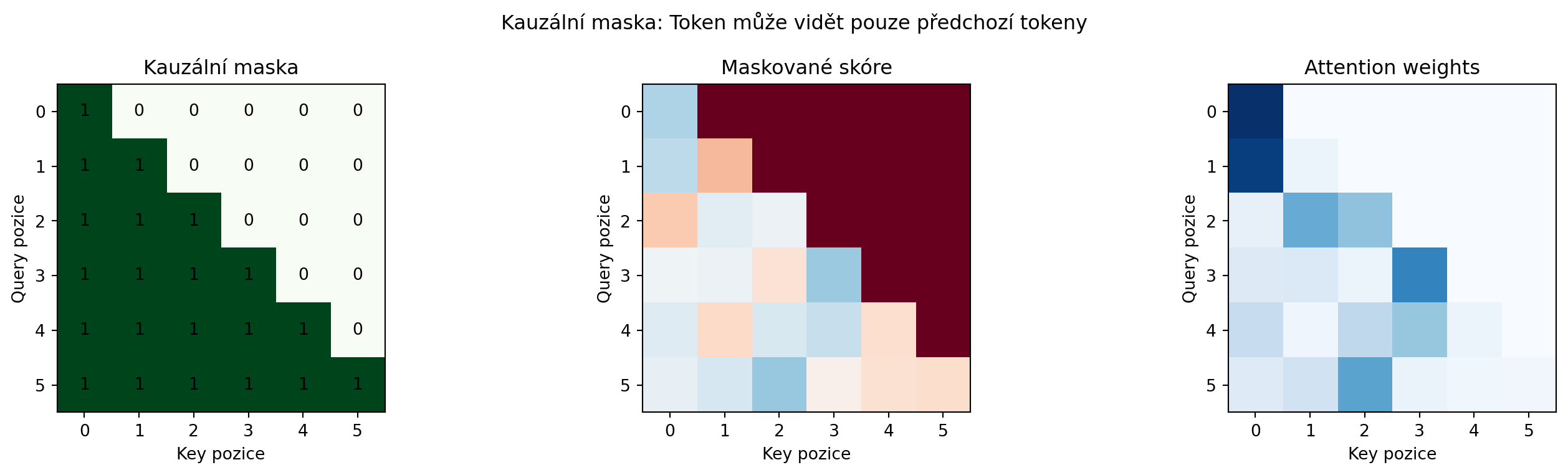
### Příklad 2: Kauzální maska
**Zadání**: Vysvětlete a vizualizujte kauzální masku pro autoregresivní modely.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
seq_len = 6
# Kauzální maska - dolní trojúhelníková matice
causal_mask = np.tril(np.ones((seq_len, seq_len)))
# Jak vypadají attention váhy s maskou
attention_scores = np.random.randn(seq_len, seq_len)
masked_scores = np.where(causal_mask, attention_scores, -1e9)
attention_weights = np.exp(masked_scores) / np.exp(masked_scores).sum(axis=-1, keepdims=True)
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 4))
ax1.imshow(causal_mask, cmap='Greens')
ax1.set_title('Kauzální maska')
ax1.set_xlabel('Key pozice')
ax1.set_ylabel('Query pozice')
for i in range(seq_len):
for j in range(seq_len):
ax1.text(j, i, int(causal_mask[i, j]), ha='center', va='center')
ax2.imshow(masked_scores, cmap='RdBu', vmin=-5, vmax=5)
ax2.set_title('Maskované skóre')
ax2.set_xlabel('Key pozice')
ax2.set_ylabel('Query pozice')
ax3.imshow(attention_weights, cmap='Blues')
ax3.set_title('Attention weights')
ax3.set_xlabel('Key pozice')
ax3.set_ylabel('Query pozice')
plt.suptitle('Kauzální maska: Token může vidět pouze předchozí tokeny', fontsize=12)
plt.tight_layout()
plt.show()
print("Kauzální maska zajišťuje, že při predikci tokenu t")
print("model vidí pouze tokeny 1, 2, ..., t-1")
```
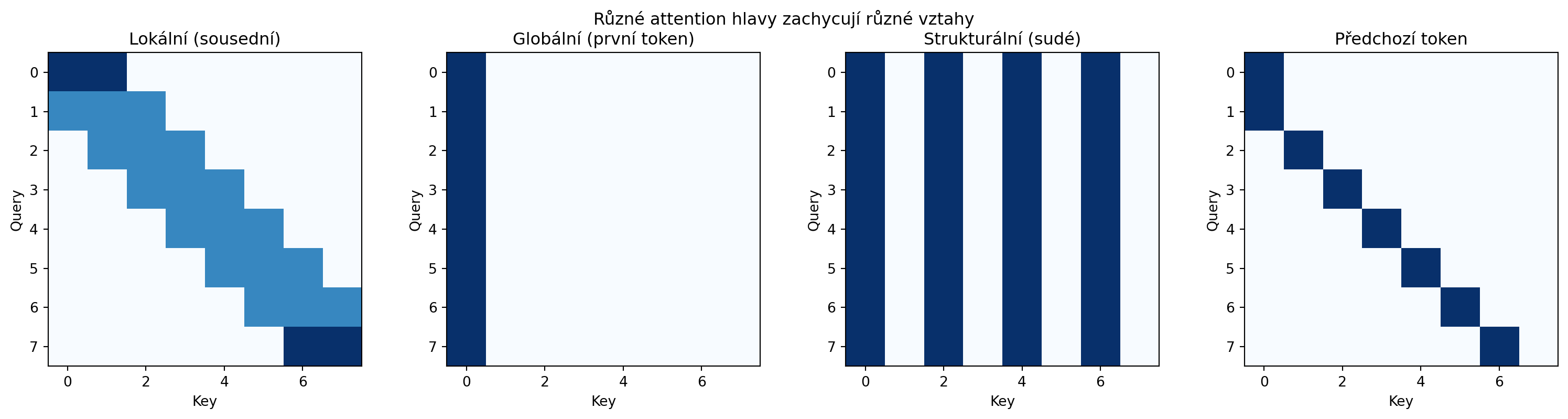
### Příklad 3: Porovnání attention hlav
**Zadání**: Ukažte, jak různé attention hlavy zachycují různé vztahy.
**Řešení**:
```{python}
# Simulace specializovaných hlav
import numpy as np
import matplotlib.pyplot as plt
seq_len = 8
# Hlava 1: Lokální attention (sousední tokeny)
local_attn = np.zeros((seq_len, seq_len))
for i in range(seq_len):
for j in range(max(0, i-1), min(seq_len, i+2)):
local_attn[i, j] = 1
local_attn = local_attn / local_attn.sum(axis=1, keepdims=True)
# Hlava 2: Globální attention (první token)
global_attn = np.zeros((seq_len, seq_len))
global_attn[:, 0] = 1
global_attn = global_attn / global_attn.sum(axis=1, keepdims=True)
# Hlava 3: Syntaktická attention (sudé tokeny)
syntactic_attn = np.zeros((seq_len, seq_len))
syntactic_attn[:, ::2] = 1
syntactic_attn = syntactic_attn / syntactic_attn.sum(axis=1, keepdims=True)
# Hlava 4: Předchozí token
prev_attn = np.zeros((seq_len, seq_len))
for i in range(seq_len):
if i > 0:
prev_attn[i, i-1] = 1
else:
prev_attn[i, i] = 1
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
heads = [
(local_attn, 'Lokální (sousední)'),
(global_attn, 'Globální (první token)'),
(syntactic_attn, 'Strukturální (sudé)'),
(prev_attn, 'Předchozí token')
]
for ax, (attn, title) in zip(axes, heads):
ax.imshow(attn, cmap='Blues')
ax.set_title(title)
ax.set_xlabel('Key')
ax.set_ylabel('Query')
plt.suptitle('Různé attention hlavy zachycují různé vztahy', fontsize=12)
plt.tight_layout()
plt.show()
```
## Matematika za transformery - shrnutí
```{python}
# Přehled všech konceptů z knihy použitých v transformerech
import matplotlib.pyplot as plt
concepts = [
("Vektory a matice", "Embeddingy slov, váhové matice W_Q, W_K, W_V"),
("Maticové násobení", "QK^T pro attention skóre, projekce"),
("Softmax", "Převod skóre na pravděpodobnosti"),
("Derivace", "Gradienty pro trénink"),
("Řetízkové pravidlo", "Backpropagation skrz attention"),
("Pravděpodobnost", "Podmíněná pravděpodobnost dalšího tokenu"),
("Cross-entropy", "Loss funkce pro jazykové modelování"),
("Gradient descent", "Optimalizace (Adam)"),
("Normální rozdělení", "Inicializace vah, dropout"),
]
fig, ax = plt.subplots(figsize=(12, 8))
ax.axis('off')
ax.text(0.5, 0.95, 'Matematika v Transformerech', ha='center', fontsize=16,
fontweight='bold', transform=ax.transAxes)
y = 0.85
for concept, usage in concepts:
ax.text(0.1, y, f"• {concept}:", fontsize=12, fontweight='bold',
transform=ax.transAxes)
ax.text(0.4, y, usage, fontsize=11, transform=ax.transAxes)
y -= 0.08
ax.text(0.5, 0.05, 'Všechny koncepty z této knihy se spojují v architektuře Transformer!',
ha='center', fontsize=12, style='italic', transform=ax.transAxes)
plt.tight_layout()
plt.show()
```
## Cvičení
::: {.callout-note icon=false}
## Cvičení 1: Implementace attention
Implementujte scaled dot-product attention v čistém NumPy včetně kauzální masky.
:::
::: {.callout-note icon=false}
## Cvičení 2: Pozicové kódování
Navrhněte alternativní pozicové kódování (např. learnable embeddings) a porovnejte se sinusoidálním.
:::
::: {.callout-note icon=false}
## Cvičení 3: Vizualizace attention
Pro natrénovaný jazykový model vizualizujte attention patterns. Jaké vzory pozorujete?
:::
::: {.callout-note icon=false}
## Cvičení 4: Mini transformer
Natrénujte mini-transformer na jednoduché úloze (např. kopírování sekvence nebo sčítání).
:::
::: {.callout-note icon=false}
## Cvičení 5: Efektivita
Spočítejte, kolik operací (FLOPs) vyžaduje jeden forward pass transformeru. Jak škáluje s délkou sekvence?
:::
## Shrnutí
::: {.callout-tip}
## Co jsme se naučili
1. **Attention** mechanismus umožňuje dynamické zaměření na relevantní části vstupu
2. **Scaled dot-product attention**: $\text{softmax}(QK^T/\sqrt{d_k})V$
3. **Multi-head attention** kombinuje více specializovaných "pohledů"
4. **Pozicové kódování** přidává informaci o pořadí tokenů
5. **Transformer blok** = Self-Attention + FFN + Residual + LayerNorm
6. **Kauzální maska** zajišťuje autoregresivní generování
7. Transformery využívají **všechny koncepty** z této knihy
:::
::: {.callout-important}
## Klíčové vzorce
- **Attention**: $\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$
- **Multi-Head**: $\text{MultiHead} = \text{Concat}(\text{head}_1, \ldots, \text{head}_h)W^O$
- **Pozicové kódování**: $PE_{(pos, 2i)} = \sin(pos / 10000^{2i/d})$
- **Transformer blok**: $x = \text{LayerNorm}(x + \text{Attention}(x))$
:::
## Závěr knihy
Gratulujeme! Prošli jste celou cestu od základních funkcí až po architekturu, která stojí za moderními jazykovými modely.
**Co jste se naučili:**
1. **Funkce a grafy** - základní stavební kameny
2. **Vektory a matice** - reprezentace dat a transformace
3. **Derivace a gradient** - měření změny a směr optimalizace
4. **Pravděpodobnost** - modelování nejistoty
5. **Optimalizace** - jak se modely učí
6. **Neuronové sítě** - od perceptronu po transformery
Nyní máte matematické základy pro pochopení a práci s moderními modely strojového učení. Další kroky mohou zahrnovat:
- Hlubší studium konkrétních architektur (BERT, GPT, ViT)
- Praktické projekty s PyTorch nebo TensorFlow
- Pokročilá témata (attention mechanisms, efficient transformers)
- Výzkum v oblasti AI
**Hodně štěstí na vaší cestě!**