# Perceptron {#sec-perceptron}
## Motivace: Inspirace mozkem
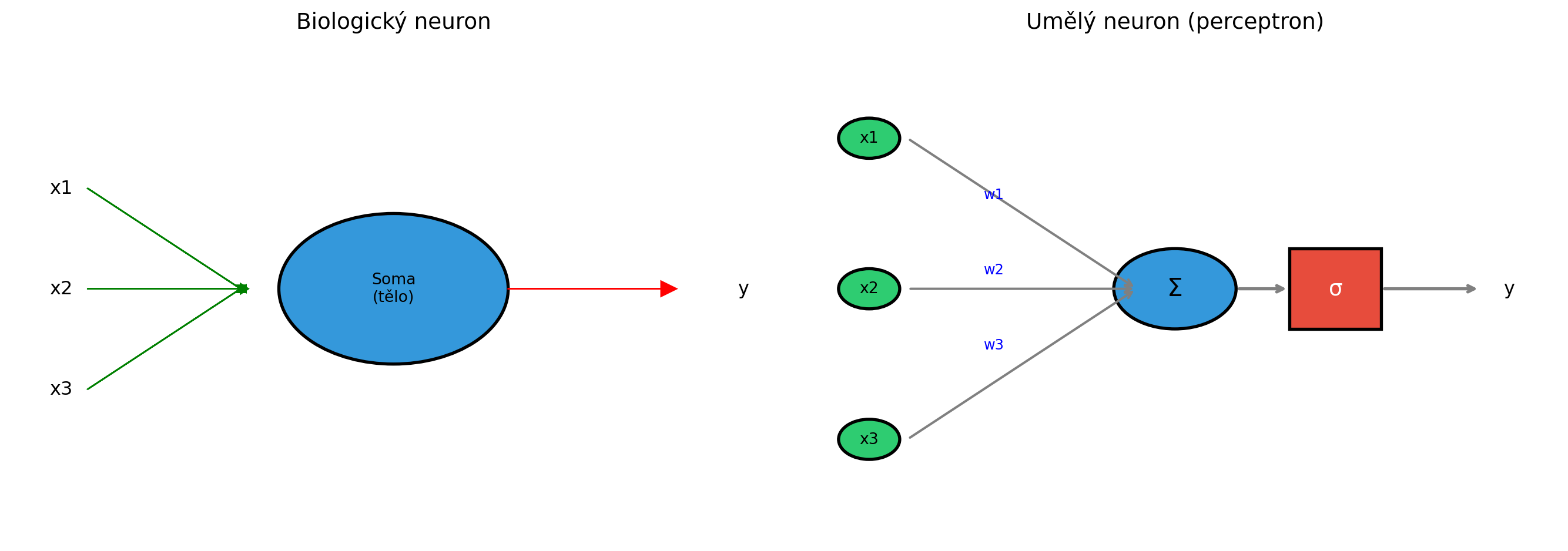
Lidský mozek obsahuje přibližně 86 miliard neuronů, propojených biliony synapsí. Každý neuron přijímá signály od ostatních neuronů, zpracovává je a pokud je celkový signál dostatečně silný, "vystřelí" a pošle signál dál.
V roce 1958 Frank Rosenblatt navrhl **perceptron** - zjednodušený matematický model neuronu. I když je perceptron velmi jednoduchý, je základním stavebním kamenem všech moderních neuronových sítí.
```{python}
import numpy as np
import matplotlib.pyplot as plt
# Vizualizace biologického vs umělého neuronu
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))
# Biologický neuron (schéma)
ax1.set_xlim(0, 10)
ax1.set_ylim(0, 10)
# Tělo neuronu
circle = plt.Circle((5, 5), 1.5, color='#3498db', ec='black', lw=2)
ax1.add_patch(circle)
ax1.text(5, 5, 'Soma\n(tělo)', ha='center', va='center', fontsize=10)
# Dendrity (vstupy)
for i, y in enumerate([7, 5, 3]):
ax1.arrow(1, y, 2, 5-y if y != 5 else 0, head_width=0.2, head_length=0.1, fc='green', ec='green')
ax1.text(0.5, y, f'x{i+1}', fontsize=12, va='center')
# Axon (výstup)
ax1.arrow(6.5, 5, 2, 0, head_width=0.3, head_length=0.2, fc='red', ec='red')
ax1.text(9.5, 5, 'y', fontsize=12, va='center')
ax1.set_title('Biologický neuron', fontsize=14)
ax1.axis('off')
# Umělý neuron (perceptron)
ax2.set_xlim(0, 10)
ax2.set_ylim(0, 10)
# Vstupní uzly
for i, y in enumerate([8, 5, 2]):
circle = plt.Circle((1, y), 0.4, color='#2ecc71', ec='black', lw=2)
ax2.add_patch(circle)
ax2.text(1, y, f'x{i+1}', ha='center', va='center', fontsize=10)
# Váhy
ax2.annotate('', xy=(4.5, 5), xytext=(1.5, y),
arrowprops=dict(arrowstyle='->', color='gray', lw=1.5))
ax2.text(2.5, (y + 5)/2 + 0.3, f'w{i+1}', fontsize=9, color='blue')
# Suma a aktivace
circle = plt.Circle((5, 5), 0.8, color='#3498db', ec='black', lw=2)
ax2.add_patch(circle)
ax2.text(5, 5, 'Σ', ha='center', va='center', fontsize=16)
# Aktivační funkce
rect = plt.Rectangle((6.5, 4.2), 1.2, 1.6, color='#e74c3c', ec='black', lw=2)
ax2.add_patch(rect)
ax2.text(7.1, 5, 'σ', ha='center', va='center', fontsize=14, color='white')
ax2.annotate('', xy=(6.5, 5), xytext=(5.8, 5),
arrowprops=dict(arrowstyle='->', color='gray', lw=2))
ax2.annotate('', xy=(9, 5), xytext=(7.7, 5),
arrowprops=dict(arrowstyle='->', color='gray', lw=2))
ax2.text(9.3, 5, 'y', fontsize=12, va='center')
ax2.set_title('Umělý neuron (perceptron)', fontsize=14)
ax2.axis('off')
plt.tight_layout()
plt.show()
```
## Matematický model perceptronu
::: {.callout-note}
## Definice: Perceptron
Perceptron počítá vážený součet vstupů a aplikuje aktivační funkci:
$$y = \sigma\left(\sum_{i=1}^n w_i x_i + b\right) = \sigma(\mathbf{w}^T \mathbf{x} + b)$$
kde:
- $\mathbf{x} = (x_1, \ldots, x_n)$ jsou vstupy
- $\mathbf{w} = (w_1, \ldots, w_n)$ jsou váhy
- $b$ je bias (práh)
- $\sigma$ je aktivační funkce
:::
```{python}
import numpy as np
def perceptron(x, w, b, activation='step'):
"""
Výpočet perceptronu.
Args:
x: Vstupní vektor
w: Vektor vah
b: Bias
activation: Aktivační funkce ('step', 'sigmoid', 'relu')
"""
# Vážený součet
z = np.dot(w, x) + b
# Aktivační funkce
if activation == 'step':
return 1 if z >= 0 else 0
elif activation == 'sigmoid':
return 1 / (1 + np.exp(-z))
elif activation == 'relu':
return max(0, z)
# Příklad
x = np.array([1.0, 0.5])
w = np.array([0.5, -0.3])
b = 0.1
print(f"Vstup: x = {x}")
print(f"Váhy: w = {w}")
print(f"Bias: b = {b}")
print(f"\nVážený součet: z = {np.dot(w, x) + b:.3f}")
print(f"Výstup (step): {perceptron(x, w, b, 'step')}")
print(f"Výstup (sigmoid): {perceptron(x, w, b, 'sigmoid'):.4f}")
print(f"Výstup (relu): {perceptron(x, w, b, 'relu'):.4f}")
```
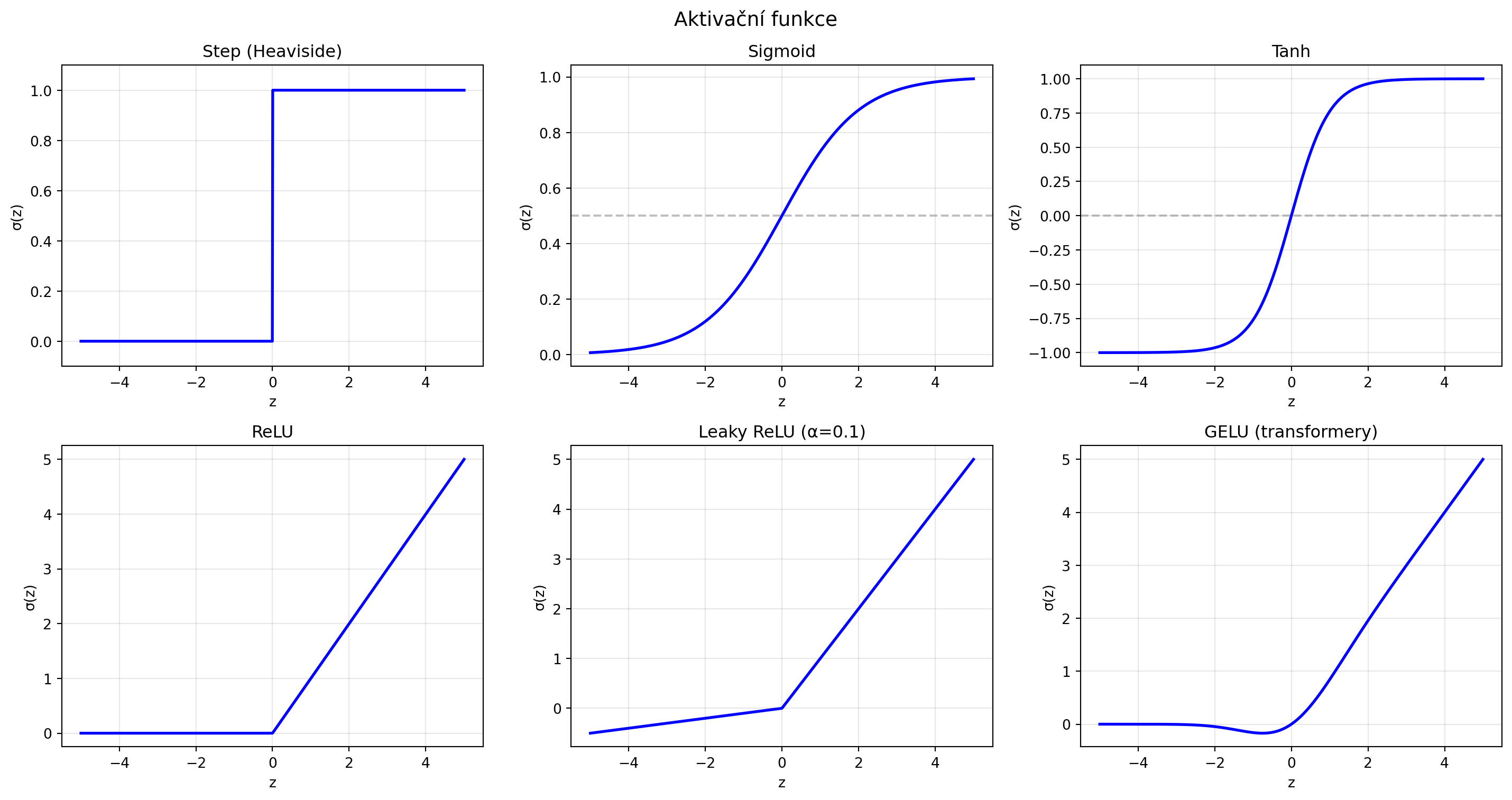
## Aktivační funkce
Aktivační funkce vnáší do sítě **nelinearitu** - bez ní by celá síť byla jen lineární transformace.
### Skoková funkce (Step)
Původní aktivační funkce perceptronu:
$$\sigma(z) = \begin{cases} 1 & \text{pokud } z \geq 0 \\ 0 & \text{pokud } z < 0 \end{cases}$$
```{python}
import numpy as np
import matplotlib.pyplot as plt
z = np.linspace(-5, 5, 1000)
fig, axes = plt.subplots(2, 3, figsize=(15, 8))
# Step funkce
ax = axes[0, 0]
step = np.where(z >= 0, 1, 0)
ax.plot(z, step, 'b-', lw=2)
ax.set_title('Step (Heaviside)')
ax.set_xlabel('z')
ax.set_ylabel('σ(z)')
ax.grid(True, alpha=0.3)
ax.set_ylim(-0.1, 1.1)
# Sigmoid
ax = axes[0, 1]
sigmoid = 1 / (1 + np.exp(-z))
ax.plot(z, sigmoid, 'b-', lw=2)
ax.axhline(y=0.5, color='gray', linestyle='--', alpha=0.5)
ax.set_title('Sigmoid')
ax.set_xlabel('z')
ax.set_ylabel('σ(z)')
ax.grid(True, alpha=0.3)
# Tanh
ax = axes[0, 2]
tanh = np.tanh(z)
ax.plot(z, tanh, 'b-', lw=2)
ax.axhline(y=0, color='gray', linestyle='--', alpha=0.5)
ax.set_title('Tanh')
ax.set_xlabel('z')
ax.set_ylabel('σ(z)')
ax.grid(True, alpha=0.3)
# ReLU
ax = axes[1, 0]
relu = np.maximum(0, z)
ax.plot(z, relu, 'b-', lw=2)
ax.set_title('ReLU')
ax.set_xlabel('z')
ax.set_ylabel('σ(z)')
ax.grid(True, alpha=0.3)
# Leaky ReLU
ax = axes[1, 1]
leaky_relu = np.where(z >= 0, z, 0.1 * z)
ax.plot(z, leaky_relu, 'b-', lw=2)
ax.set_title('Leaky ReLU (α=0.1)')
ax.set_xlabel('z')
ax.set_ylabel('σ(z)')
ax.grid(True, alpha=0.3)
# GELU (používá se v transformerech)
ax = axes[1, 2]
from math import erf as math_erf
gelu = 0.5 * z * (1 + np.array([math_erf(zi / np.sqrt(2)) for zi in z]))
ax.plot(z, gelu, 'b-', lw=2)
ax.set_title('GELU (transformery)')
ax.set_xlabel('z')
ax.set_ylabel('σ(z)')
ax.grid(True, alpha=0.3)
plt.suptitle('Aktivační funkce', fontsize=14)
plt.tight_layout()
plt.show()
```
### Porovnání aktivačních funkcí
```{python}
aktivace = {
'Step': ('Původní, nediferencovatelná', 'Historická'),
'Sigmoid': ('Výstup v (0,1), hladká', 'Výstupní vrstva, binární klasifikace'),
'Tanh': ('Výstup v (-1,1), zero-centered', 'RNN, skryté vrstvy'),
'ReLU': ('Rychlá, řeší vanishing gradient', 'Default pro skryté vrstvy'),
'Leaky ReLU': ('Řeší "dying ReLU"', 'Alternativa k ReLU'),
'GELU': ('Hladká aproximace ReLU', 'Transformery (BERT, GPT)')
}
print("Přehled aktivačních funkcí:")
print("=" * 70)
for name, (vlastnosti, pouziti) in aktivace.items():
print(f"\n{name}:")
print(f" Vlastnosti: {vlastnosti}")
print(f" Použití: {pouziti}")
```
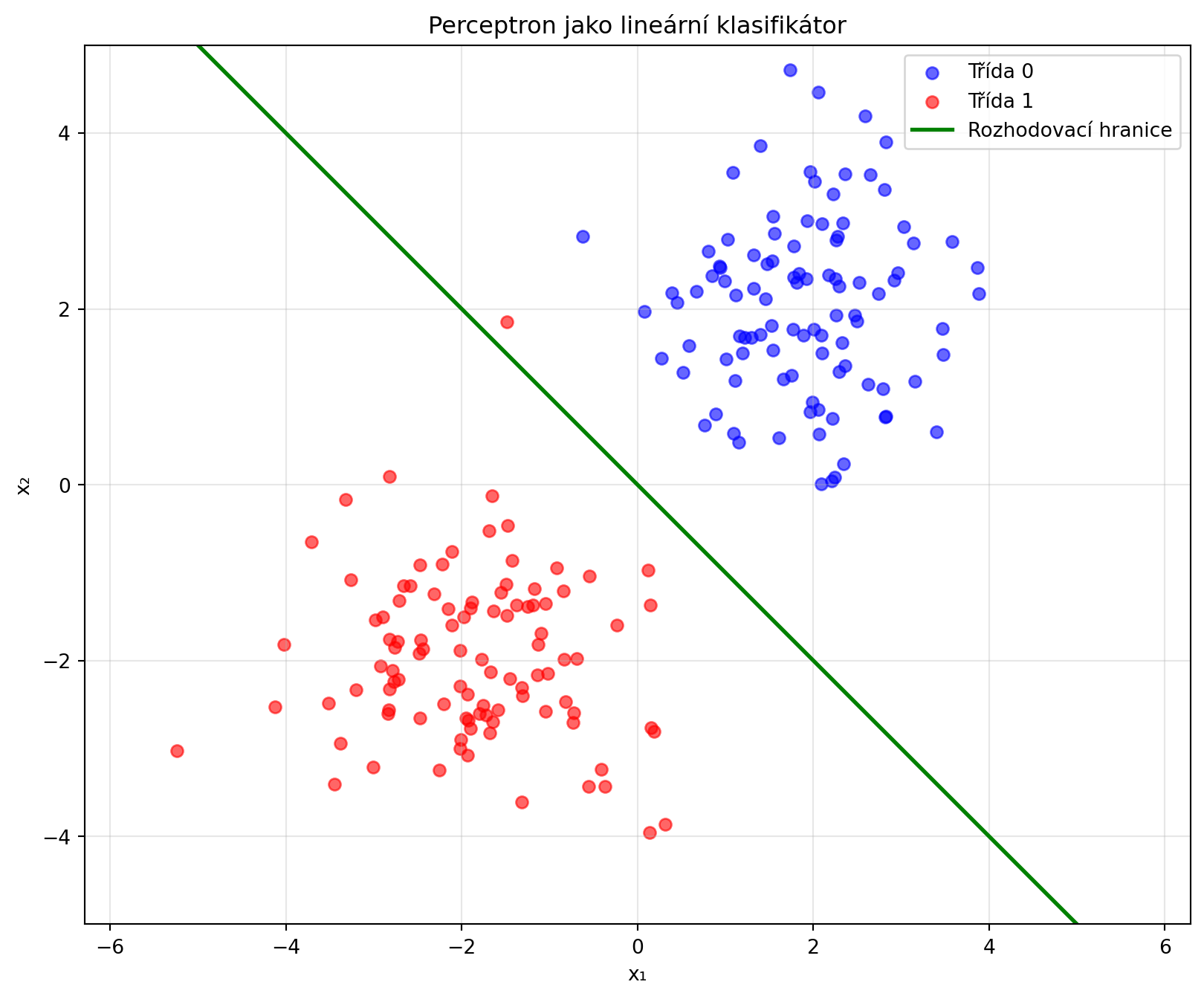
## Perceptron jako lineární klasifikátor
Perceptron rozděluje prostor **nadrovinou** (v 2D přímkou):
```{python}
# Perceptron se naučí rozhodovací hranici
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
# Generování dat - dvě lineárně oddělitelné třídy
n_samples = 100
X_class0 = np.random.randn(n_samples, 2) + np.array([2, 2])
X_class1 = np.random.randn(n_samples, 2) + np.array([-2, -2])
X = np.vstack([X_class0, X_class1])
y = np.array([0] * n_samples + [1] * n_samples)
# Vizualizace
plt.figure(figsize=(10, 8))
plt.scatter(X_class0[:, 0], X_class0[:, 1], c='blue', label='Třída 0', alpha=0.6)
plt.scatter(X_class1[:, 0], X_class1[:, 1], c='red', label='Třída 1', alpha=0.6)
# Nakreslíme možnou rozhodovací hranici
x_line = np.linspace(-5, 5, 100)
# w1*x + w2*y + b = 0 => y = -(w1*x + b)/w2
w = np.array([1, 1])
b = 0
y_line = -(w[0] * x_line + b) / w[1]
plt.plot(x_line, y_line, 'g-', lw=2, label='Rozhodovací hranice')
plt.xlabel('x₁')
plt.ylabel('x₂')
plt.title('Perceptron jako lineární klasifikátor')
plt.legend()
plt.axis('equal')
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.grid(True, alpha=0.3)
plt.show()
```
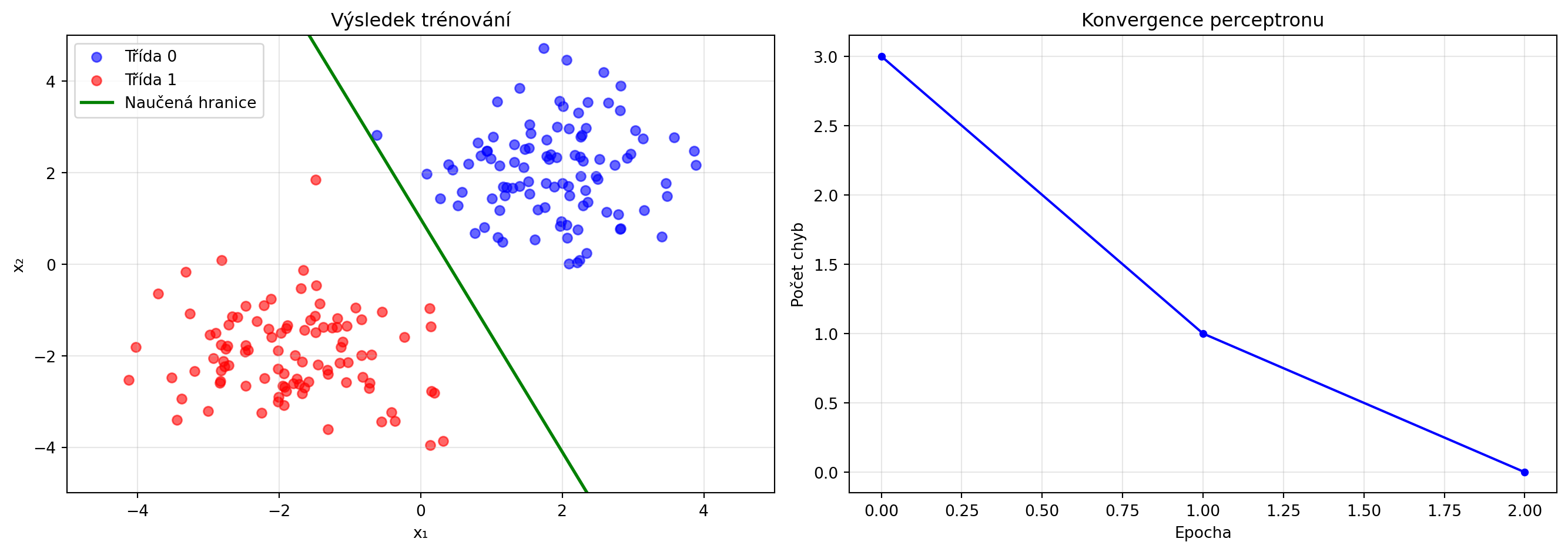
### Trénování perceptronu
```{python}
import numpy as np
import matplotlib.pyplot as plt
def train_perceptron(X, y, lr=0.1, n_epochs=100):
"""
Trénování perceptronu pomocí perceptron learning rule.
"""
n_samples, n_features = X.shape
w = np.zeros(n_features)
b = 0
history = {'weights': [w.copy()], 'bias': [b], 'errors': []}
for epoch in range(n_epochs):
errors = 0
for xi, yi in zip(X, y):
# Predikce
z = np.dot(w, xi) + b
y_pred = 1 if z >= 0 else 0
# Update při chybě
if y_pred != yi:
errors += 1
update = lr * (yi - y_pred)
w += update * xi
b += update
history['weights'].append(w.copy())
history['bias'].append(b)
history['errors'].append(errors)
if errors == 0:
print(f"Konvergence po {epoch + 1} epochách!")
break
return w, b, history
# Trénování
w_final, b_final, history = train_perceptron(X, y, lr=0.1, n_epochs=100)
print(f"Naučené váhy: w = {w_final}")
print(f"Naučený bias: b = {b_final:.4f}")
# Vizualizace tréninku
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))
# Data a finální hranice
ax1.scatter(X_class0[:, 0], X_class0[:, 1], c='blue', label='Třída 0', alpha=0.6)
ax1.scatter(X_class1[:, 0], X_class1[:, 1], c='red', label='Třída 1', alpha=0.6)
x_line = np.linspace(-5, 5, 100)
y_line = -(w_final[0] * x_line + b_final) / w_final[1]
ax1.plot(x_line, y_line, 'g-', lw=2, label='Naučená hranice')
ax1.set_xlabel('x₁')
ax1.set_ylabel('x₂')
ax1.set_title('Výsledek trénování')
ax1.legend()
ax1.set_xlim(-5, 5)
ax1.set_ylim(-5, 5)
ax1.grid(True, alpha=0.3)
# Chyby v čase
ax2.plot(history['errors'], 'b.-', markersize=8)
ax2.set_xlabel('Epocha')
ax2.set_ylabel('Počet chyb')
ax2.set_title('Konvergence perceptronu')
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
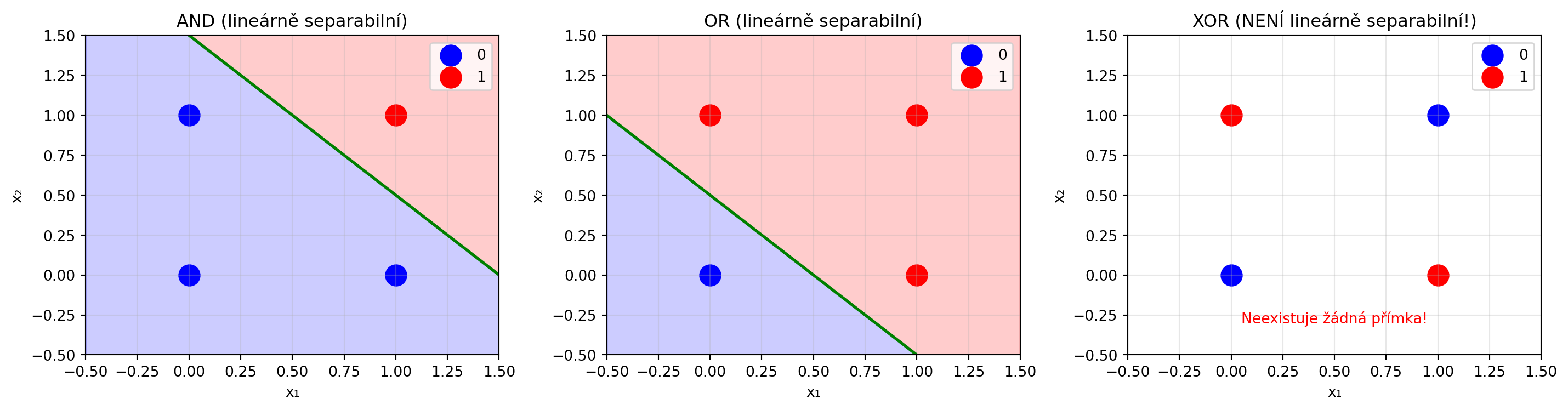
## Limity perceptronu: Problém XOR
Perceptron může naučit jen **lineárně separabilní** problémy. Slavný příklad problému, který perceptron nezvládne, je **XOR**:
```{python}
# XOR problém
import numpy as np
import matplotlib.pyplot as plt
X_xor = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y_xor = np.array([0, 1, 1, 0]) # XOR výstup
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# AND - lineárně separabilní
ax = axes[0]
X_and = X_xor
y_and = np.array([0, 0, 0, 1])
ax.scatter(X_and[y_and==0, 0], X_and[y_and==0, 1], c='blue', s=200, label='0')
ax.scatter(X_and[y_and==1, 0], X_and[y_and==1, 1], c='red', s=200, label='1')
# Rozhodovací hranice
x_line = np.linspace(-0.5, 1.5, 100)
ax.plot(x_line, 1.5 - x_line, 'g-', lw=2)
ax.fill_between(x_line, 1.5 - x_line, 2, alpha=0.2, color='red')
ax.fill_between(x_line, -0.5, 1.5 - x_line, alpha=0.2, color='blue')
ax.set_title('AND (lineárně separabilní)')
ax.set_xlabel('x₁')
ax.set_ylabel('x₂')
ax.set_xlim(-0.5, 1.5)
ax.set_ylim(-0.5, 1.5)
ax.legend()
ax.grid(True, alpha=0.3)
# OR - lineárně separabilní
ax = axes[1]
y_or = np.array([0, 1, 1, 1])
ax.scatter(X_xor[y_or==0, 0], X_xor[y_or==0, 1], c='blue', s=200, label='0')
ax.scatter(X_xor[y_or==1, 0], X_xor[y_or==1, 1], c='red', s=200, label='1')
ax.plot(x_line, 0.5 - x_line, 'g-', lw=2)
ax.fill_between(x_line, 0.5 - x_line, 2, alpha=0.2, color='red')
ax.fill_between(x_line, -0.5, 0.5 - x_line, alpha=0.2, color='blue')
ax.set_title('OR (lineárně separabilní)')
ax.set_xlabel('x₁')
ax.set_ylabel('x₂')
ax.set_xlim(-0.5, 1.5)
ax.set_ylim(-0.5, 1.5)
ax.legend()
ax.grid(True, alpha=0.3)
# XOR - NENÍ lineárně separabilní
ax = axes[2]
ax.scatter(X_xor[y_xor==0, 0], X_xor[y_xor==0, 1], c='blue', s=200, label='0')
ax.scatter(X_xor[y_xor==1, 0], X_xor[y_xor==1, 1], c='red', s=200, label='1')
ax.set_title('XOR (NENÍ lineárně separabilní!)')
ax.set_xlabel('x₁')
ax.set_ylabel('x₂')
ax.set_xlim(-0.5, 1.5)
ax.set_ylim(-0.5, 1.5)
ax.legend()
ax.grid(True, alpha=0.3)
ax.text(0.5, -0.3, 'Neexistuje žádná přímka!', ha='center', fontsize=10, color='red')
plt.tight_layout()
plt.show()
print("XOR problém ukázal limity perceptronu.")
print("Řešení: Více vrstev (multi-layer perceptron)!")
```
## Perceptron v PyTorch
```{python}
import torch
import torch.nn as nn
# Definice perceptronu jako PyTorch modul
class Perceptron(nn.Module):
def __init__(self, input_size):
super().__init__()
self.linear = nn.Linear(input_size, 1)
self.activation = nn.Sigmoid()
def forward(self, x):
z = self.linear(x)
return self.activation(z)
# Vytvoření a test
torch.manual_seed(42)
model = Perceptron(input_size=2)
# Test
x_test = torch.tensor([[1.0, 0.5]])
output = model(x_test)
print("Perceptron v PyTorch:")
print(f"Vstup: {x_test.numpy()}")
print(f"Váhy: {model.linear.weight.data.numpy()}")
print(f"Bias: {model.linear.bias.data.numpy()}")
print(f"Výstup: {output.item():.4f}")
```
### Trénování perceptronu v PyTorch
```{python}
# Data
import numpy as np
import matplotlib.pyplot as plt
X_tensor = torch.FloatTensor(X)
y_tensor = torch.FloatTensor(y).unsqueeze(1)
# Model, loss, optimizer
model = Perceptron(input_size=2)
criterion = nn.BCELoss() # Binary Cross-Entropy
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
# Trénink
losses = []
for epoch in range(100):
# Forward
y_pred = model(X_tensor)
loss = criterion(y_pred, y_tensor)
# Backward
optimizer.zero_grad()
loss.backward()
optimizer.step()
losses.append(loss.item())
# Výsledky
with torch.no_grad():
predictions = (model(X_tensor) > 0.5).float()
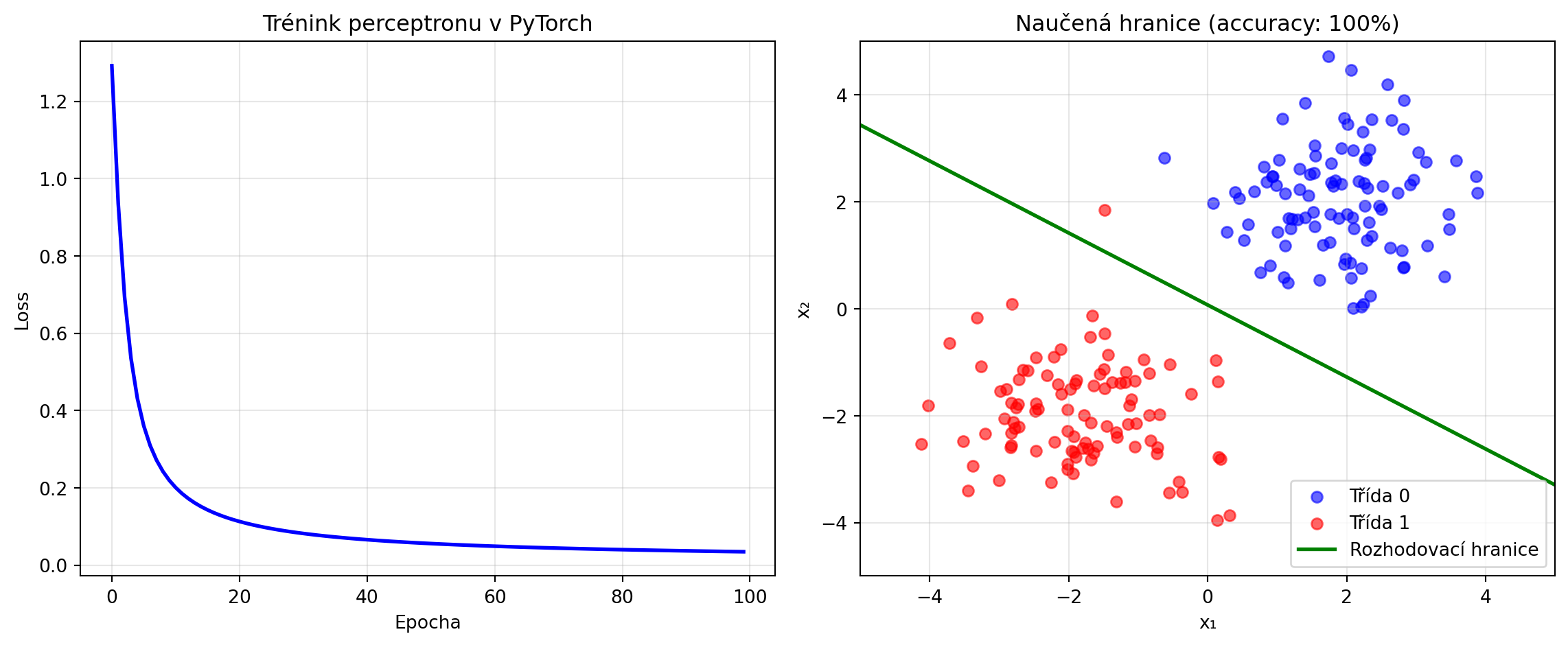
accuracy = (predictions == y_tensor).float().mean()
print(f"Přesnost: {accuracy.item():.2%}")
# Vizualizace
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
ax1.plot(losses, 'b-', lw=2)
ax1.set_xlabel('Epocha')
ax1.set_ylabel('Loss')
ax1.set_title('Trénink perceptronu v PyTorch')
ax1.grid(True, alpha=0.3)
# Rozhodovací hranice
w = model.linear.weight.data.numpy()[0]
b = model.linear.bias.data.numpy()[0]
ax2.scatter(X_class0[:, 0], X_class0[:, 1], c='blue', label='Třída 0', alpha=0.6)
ax2.scatter(X_class1[:, 0], X_class1[:, 1], c='red', label='Třída 1', alpha=0.6)
x_line = np.linspace(-5, 5, 100)
# sigmoid(wx + b) = 0.5 => wx + b = 0
y_line = -(w[0] * x_line + b) / w[1]
ax2.plot(x_line, y_line, 'g-', lw=2, label='Rozhodovací hranice')
ax2.set_xlabel('x₁')
ax2.set_ylabel('x₂')
ax2.set_title(f'Naučená hranice (accuracy: {accuracy.item():.0%})')
ax2.legend()
ax2.set_xlim(-5, 5)
ax2.set_ylim(-5, 5)
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
## Řešené příklady
### Příklad 1: Ruční výpočet perceptronu
**Zadání**: Pro perceptron s $w = [0.5, -0.2]$ a $b = 0.1$ spočítejte výstup pro $x = [1, 2]$ s sigmoid aktivací.
**Řešení**:
```{python}
import numpy as np
w = np.array([0.5, -0.2])
b = 0.1
x = np.array([1, 2])
# Krok 1: Vážený součet
z = np.dot(w, x) + b
print(f"Krok 1: z = w·x + b = {w[0]}×{x[0]} + {w[1]}×{x[1]} + {b}")
print(f" z = {w[0]*x[0]} + {w[1]*x[1]} + {b} = {z}")
# Krok 2: Aktivace
sigmoid = 1 / (1 + np.exp(-z))
print(f"\nKrok 2: σ(z) = 1/(1 + e^(-{z:.1f})) = {sigmoid:.4f}")
print(f"\nVýstup perceptronu: {sigmoid:.4f}")
print(f"Klasifikace (práh 0.5): třída {1 if sigmoid >= 0.5 else 0}")
```
### Příklad 2: Logické hradlo AND
**Zadání**: Najděte váhy perceptronu, který implementuje logické AND.
**Řešení**:
```{python}
# AND: (0,0)->0, (0,1)->0, (1,0)->0, (1,1)->1
import numpy as np
X_and = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y_and = np.array([0, 0, 0, 1])
# Trénování
w, b, _ = train_perceptron(X_and, y_and, lr=0.1, n_epochs=100)
print(f"AND hradlo:")
print(f"Váhy: w = {w}")
print(f"Bias: b = {b}")
# Test
print("\nTest:")
for xi, yi in zip(X_and, y_and):
z = np.dot(w, xi) + b
pred = 1 if z >= 0 else 0
print(f" {xi[0]} AND {xi[1]} = {pred} (očekáváno: {yi})")
```
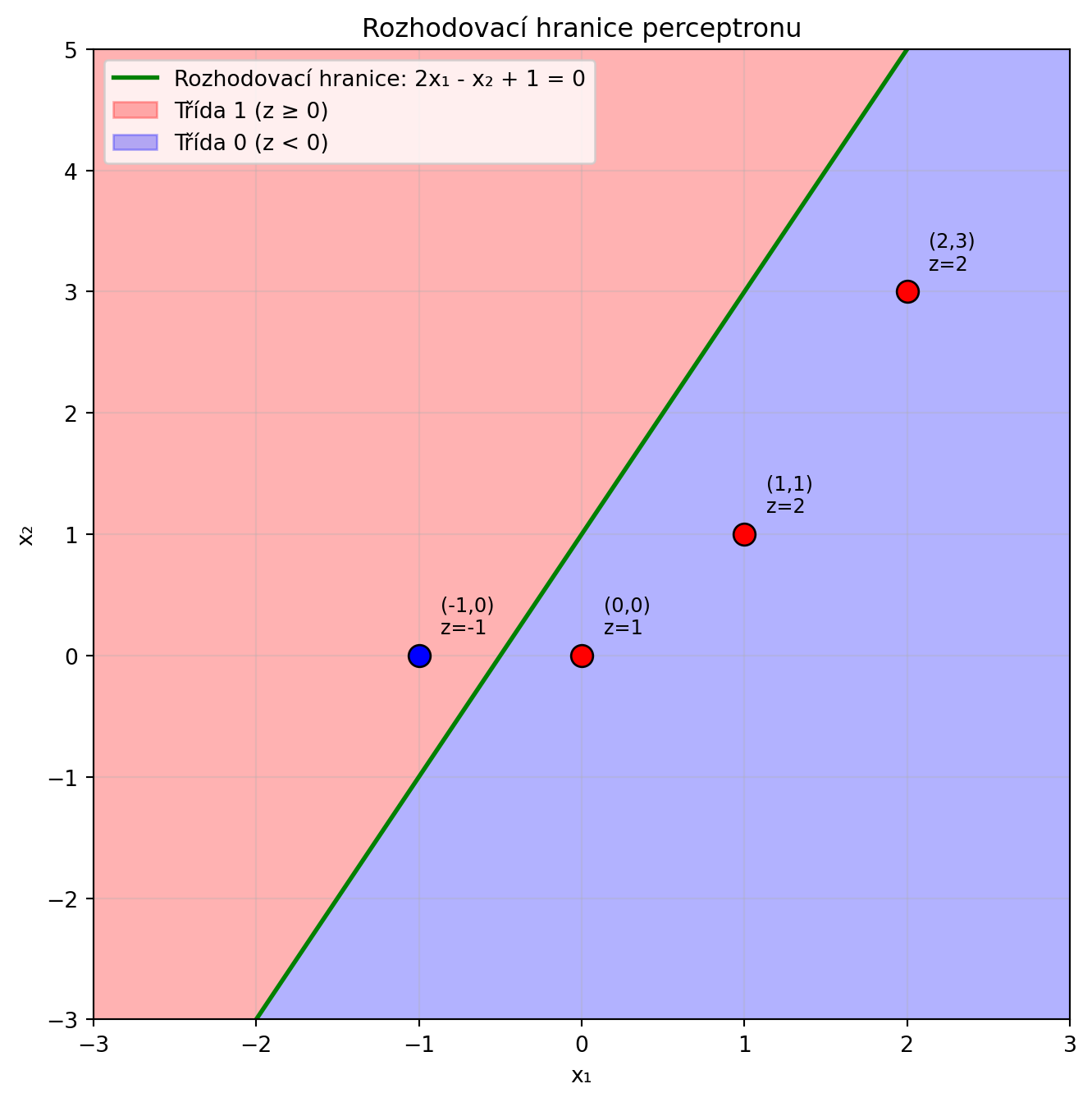
### Příklad 3: Rozhodovací hranice
**Zadání**: Pro perceptron s $w = [2, -1]$ a $b = 1$ nakreslete rozhodovací hranici.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
w = np.array([2, -1])
b = 1
# Rozhodovací hranice: w·x + b = 0
# 2*x1 - x2 + 1 = 0
# x2 = 2*x1 + 1
x1 = np.linspace(-3, 3, 100)
x2 = 2 * x1 + 1
plt.figure(figsize=(8, 8))
plt.plot(x1, x2, 'g-', lw=2, label='Rozhodovací hranice: 2x₁ - x₂ + 1 = 0')
# Oblasti
plt.fill_between(x1, x2, 10, alpha=0.3, color='red', label='Třída 1 (z ≥ 0)')
plt.fill_between(x1, -10, x2, alpha=0.3, color='blue', label='Třída 0 (z < 0)')
# Testovací body
test_points = [(0, 0), (1, 1), (-1, 0), (2, 3)]
for px, py in test_points:
z = w[0]*px + w[1]*py + b
color = 'red' if z >= 0 else 'blue'
plt.scatter([px], [py], c=color, s=100, edgecolors='black', zorder=5)
plt.annotate(f'({px},{py})\nz={z}', (px, py), textcoords="offset points",
xytext=(10, 10), fontsize=9)
plt.xlabel('x₁')
plt.ylabel('x₂')
plt.title('Rozhodovací hranice perceptronu')
plt.legend()
plt.xlim(-3, 3)
plt.ylim(-3, 5)
plt.grid(True, alpha=0.3)
plt.show()
```
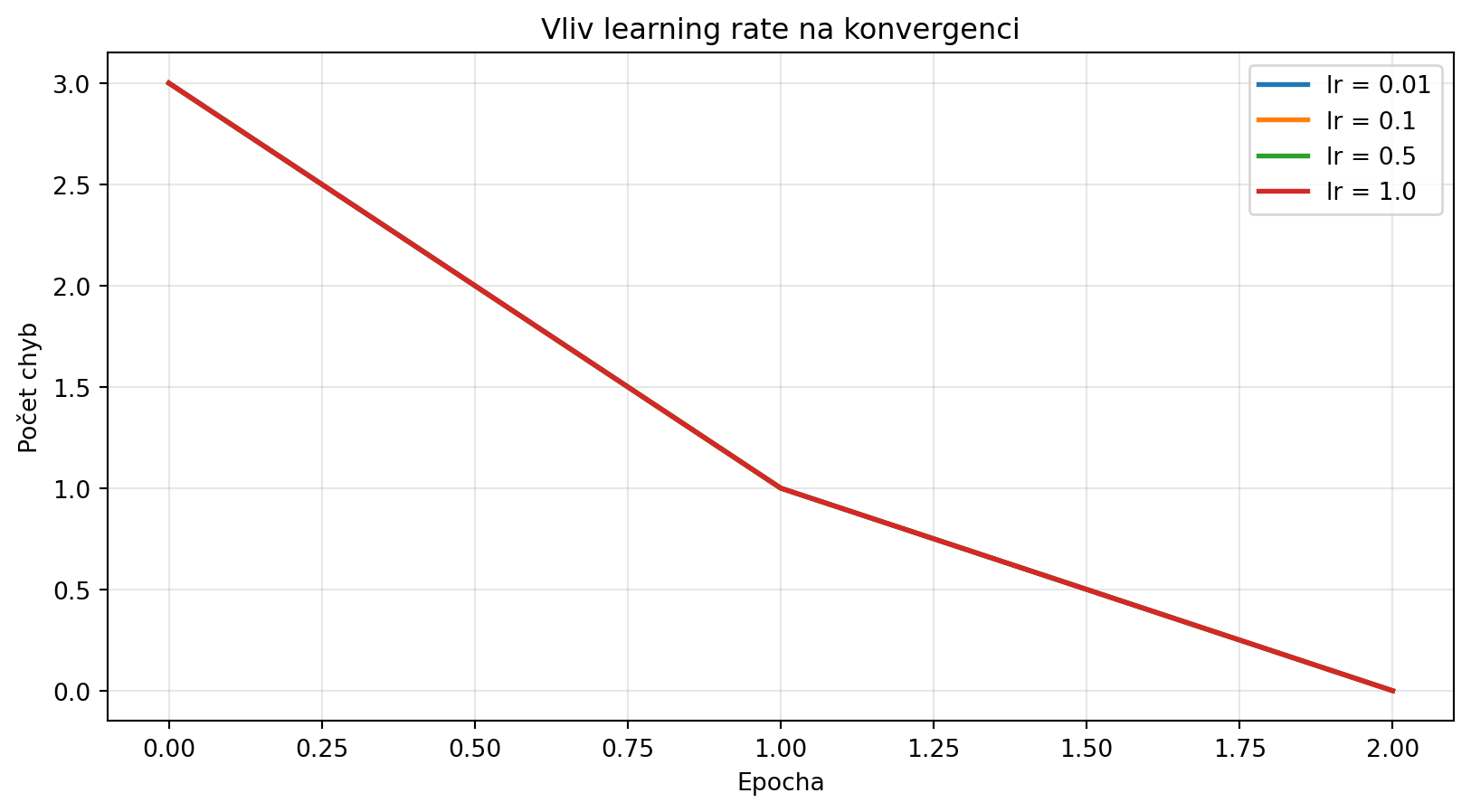
### Příklad 4: Vliv learning rate
**Zadání**: Ukažte vliv learning rate na konvergenci perceptronu.
**Řešení**:
```{python}
import matplotlib.pyplot as plt
learning_rates = [0.01, 0.1, 0.5, 1.0]
results = {}
for lr in learning_rates:
_, _, history = train_perceptron(X, y, lr=lr, n_epochs=50)
results[lr] = history['errors']
plt.figure(figsize=(10, 5))
for lr, errors in results.items():
plt.plot(errors, label=f'lr = {lr}', lw=2)
plt.xlabel('Epocha')
plt.ylabel('Počet chyb')
plt.title('Vliv learning rate na konvergenci')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
## Cvičení
::: {.callout-note icon=false}
## Cvičení 1: Logické hradlo OR
Natrénujte perceptron pro logické hradlo OR. Jaké jsou naučené váhy?
:::
::: {.callout-note icon=false}
## Cvičení 2: Logické hradlo NAND
Natrénujte perceptron pro NAND (NOT AND). Jak se liší od AND?
:::
::: {.callout-note icon=false}
## Cvičení 3: XOR pomocí více perceptronů
XOR nelze řešit jedním perceptronem, ale lze ho rozložit: XOR = (A OR B) AND NOT(A AND B). Implementujte XOR jako kombinaci tří perceptronů.
:::
::: {.callout-note icon=false}
## Cvičení 4: Klasifikace IRIS
Použijte perceptron pro binární klasifikaci na datasetu Iris (jen dvě třídy). Jaká je dosažená přesnost?
:::
::: {.callout-note icon=false}
## Cvičení 5: Vizualizace učení
Vytvořte animaci, která ukáže, jak se rozhodovací hranice perceptronu mění během tréninku.
:::
## Shrnutí
::: {.callout-tip}
## Co jsme se naučili
1. **Perceptron** je základní stavební blok neuronových sítí
2. **Vážený součet**: $z = \mathbf{w}^T \mathbf{x} + b$
3. **Aktivační funkce** vnáší nelinearitu (sigmoid, ReLU, ...)
4. Perceptron implementuje **lineární klasifikátor**
5. **Perceptron learning rule** konverguje pro lineárně separabilní data
6. **Limit**: Perceptron nezvládne XOR a jiné nelineární problémy
7. **Řešení**: Více vrstev → Multi-Layer Perceptron
:::
::: {.callout-important}
## Klíčové vzorce
- **Perceptron**: $y = \sigma(\mathbf{w}^T \mathbf{x} + b)$
- **Sigmoid**: $\sigma(z) = \frac{1}{1 + e^{-z}}$
- **ReLU**: $\sigma(z) = \max(0, z)$
- **Update**: $w \leftarrow w + \eta (y - \hat{y}) x$
:::
V další kapitole se podíváme na **vícevrstvé sítě** (Multi-Layer Perceptrons), které překonávají limity jednoduchého perceptronu a dokážou aproximovat libovolnou funkci.