# Funkce více proměnných
::: {.callout-tip title="Co se naučíte"}
V této kapitole se naučíte:
- Co je funkce více proměnných
- Co jsou parciální derivace
- Co je gradient a proč je důležitý
- Jak gradient ukazuje směr největšího růstu
- 3D vizualizace funkcí a gradientů
:::
## Proč funkce více proměnných?
V reálném světě závisí většina věcí na více faktorech:
- **Teplota** závisí na zeměpisné šířce A nadmořské výšce
- **Cena domu** závisí na rozloze A lokalitě A stáří
- **Loss neuronové sítě** závisí na TISÍCÍCH vah
V strojovém učení máme funkce s miliony proměnných (vah)!
---
## Funkce dvou proměnných
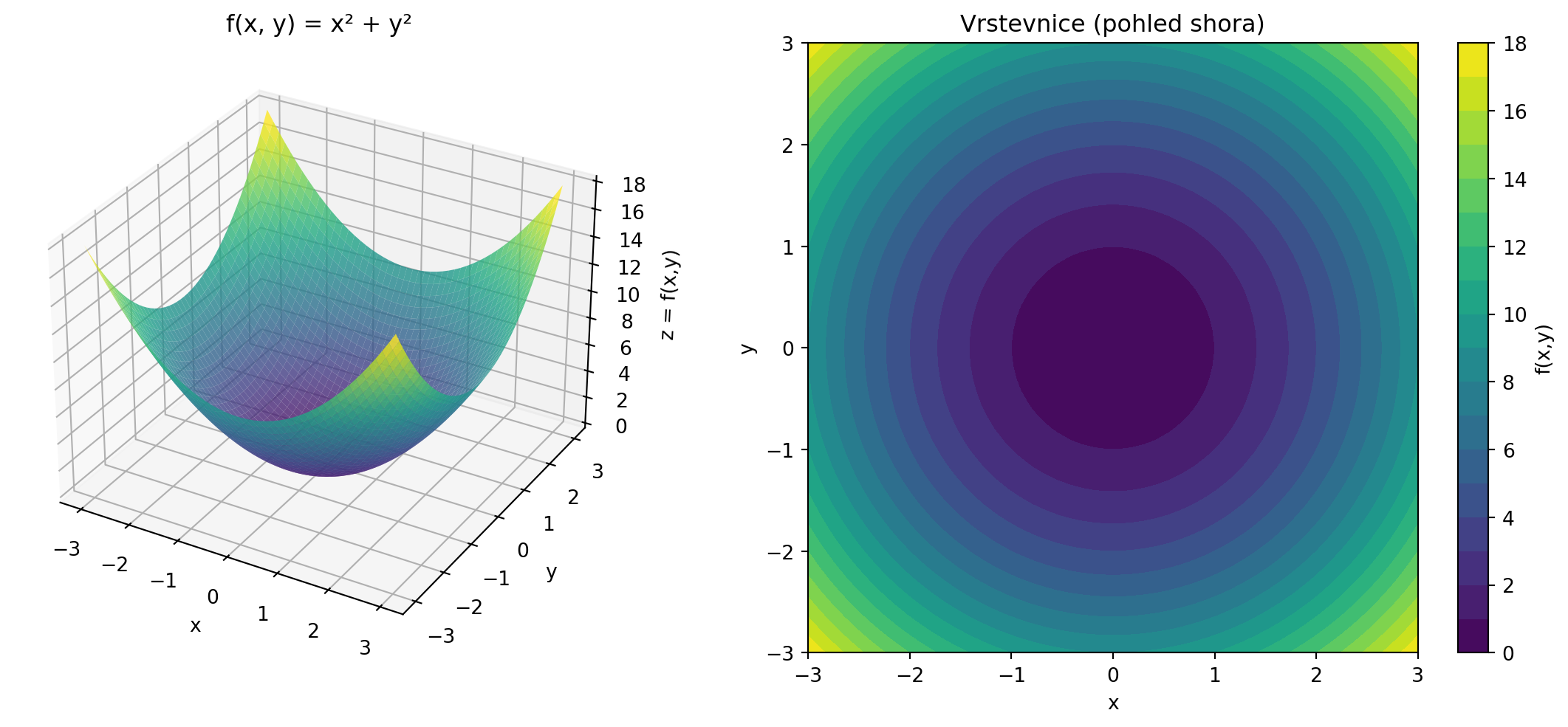
Funkce dvou proměnných $f(x, y)$ přiřazuje každé dvojici $(x, y)$ jedno číslo.
Graf takové funkce je **plocha** ve 3D prostoru.
```{python}
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Funkce dvou proměnných
def f(x, y):
return x**2 + y**2
# Vytvoření mřížky
x = np.linspace(-3, 3, 50)
y = np.linspace(-3, 3, 50)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# 3D graf
fig = plt.figure(figsize=(12, 5))
ax1 = fig.add_subplot(121, projection='3d')
ax1.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.set_zlabel('z = f(x,y)')
ax1.set_title('f(x, y) = x² + y²')
# Vrstevnice (contour plot)
ax2 = fig.add_subplot(122)
contour = ax2.contourf(X, Y, Z, levels=20, cmap='viridis')
plt.colorbar(contour, ax=ax2, label='f(x,y)')
ax2.set_xlabel('x')
ax2.set_ylabel('y')
ax2.set_title('Vrstevnice (pohled shora)')
ax2.set_aspect('equal')
plt.tight_layout()
plt.show()
```
---
## Parciální derivace
**Parciální derivace** je derivace podle jedné proměnné, zatímco ostatní držíme konstantní.
Pro funkci $f(x, y)$:
- $\frac{\partial f}{\partial x}$ -- derivace podle $x$ (y je konstanta)
- $\frac{\partial f}{\partial y}$ -- derivace podle $y$ (x je konstanta)
### Příklad
Pro $f(x, y) = x^2 + xy + y^2$:
$$\frac{\partial f}{\partial x} = 2x + y$$
$$\frac{\partial f}{\partial y} = x + 2y$$
```{python}
from sympy import symbols, diff
x, y = symbols('x y')
f = x**2 + x*y + y**2
df_dx = diff(f, x)
df_dy = diff(f, y)
print(f"f(x, y) = {f}")
print(f"∂f/∂x = {df_dx}")
print(f"∂f/∂y = {df_dy}")
```
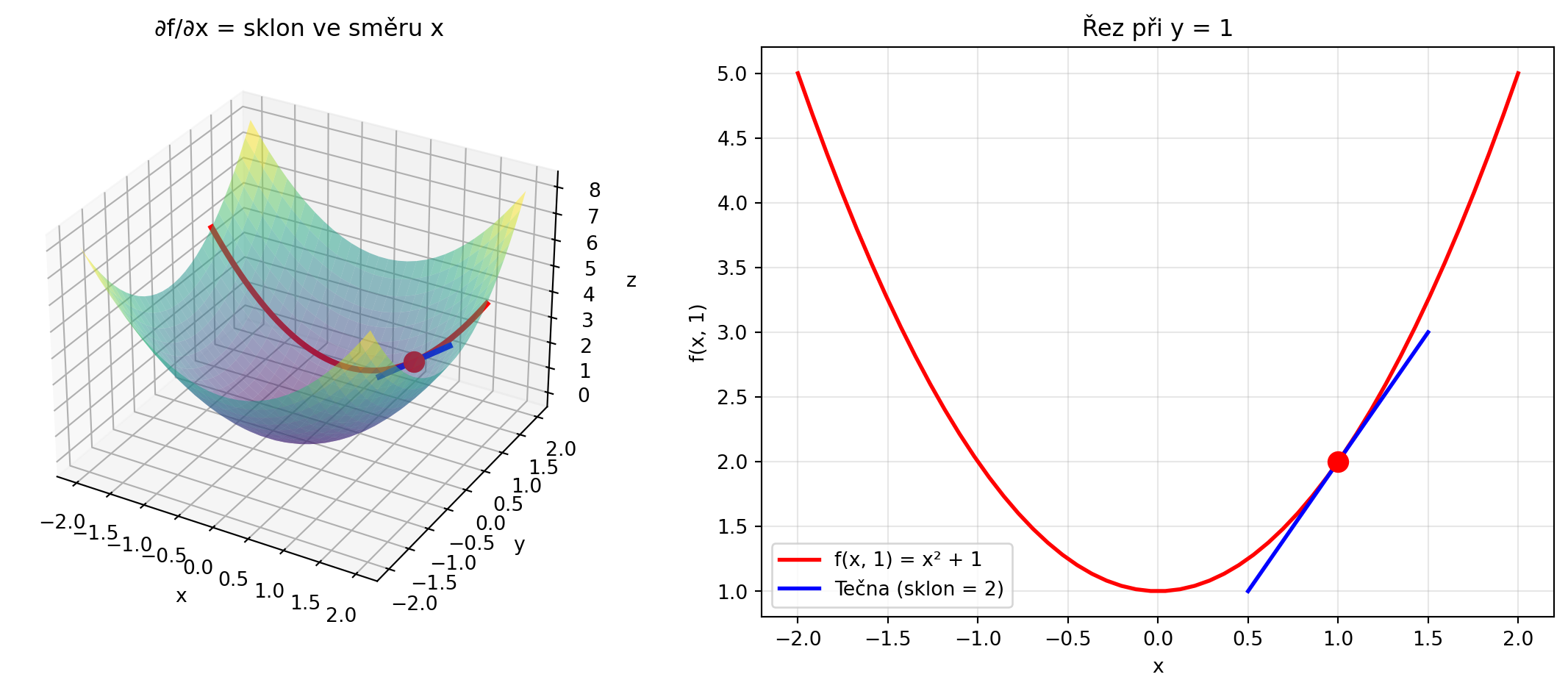
### Geometrická interpretace
Parciální derivace $\frac{\partial f}{\partial x}$ je sklon plochy ve směru osy $x$.
```{python}
#| fig-cap: "Parciální derivace jako sklon ve směru osy"
#| code-fold: true
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return x**2 + y**2
fig = plt.figure(figsize=(12, 5))
# 3D pohled
ax1 = fig.add_subplot(121, projection='3d')
x = np.linspace(-2, 2, 30)
y = np.linspace(-2, 2, 30)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
ax1.plot_surface(X, Y, Z, cmap='viridis', alpha=0.5)
# Řez při y = 1
y_fixed = 1
x_line = np.linspace(-2, 2, 50)
z_line = f(x_line, y_fixed)
ax1.plot(x_line, np.ones_like(x_line) * y_fixed, z_line, 'r-', linewidth=3,
label='Řez při y=1')
# Bod a tečna
x_bod = 1
z_bod = f(x_bod, y_fixed)
ax1.scatter([x_bod], [y_fixed], [z_bod], color='red', s=100)
# Tečna (parciální derivace ∂f/∂x = 2x = 2 v bodě x=1)
sklon = 2 * x_bod
x_tecna = np.linspace(x_bod - 0.5, x_bod + 0.5, 10)
z_tecna = z_bod + sklon * (x_tecna - x_bod)
ax1.plot(x_tecna, np.ones_like(x_tecna) * y_fixed, z_tecna, 'b-', linewidth=3)
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.set_zlabel('z')
ax1.set_title('∂f/∂x = sklon ve směru x')
# 2D pohled na řez
ax2 = fig.add_subplot(122)
ax2.plot(x_line, z_line, 'r-', linewidth=2, label='f(x, 1) = x² + 1')
ax2.plot(x_tecna, z_tecna, 'b-', linewidth=2, label='Tečna (sklon = 2)')
ax2.plot(x_bod, z_bod, 'ro', markersize=10)
ax2.set_xlabel('x')
ax2.set_ylabel('f(x, 1)')
ax2.set_title('Řez při y = 1')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
---
## Gradient
**Gradient** je vektor všech parciálních derivací:
$$\nabla f = \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix}$$
Pro více proměnných:
$$\nabla f = \begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots \\ \frac{\partial f}{\partial x_n} \end{bmatrix}$$
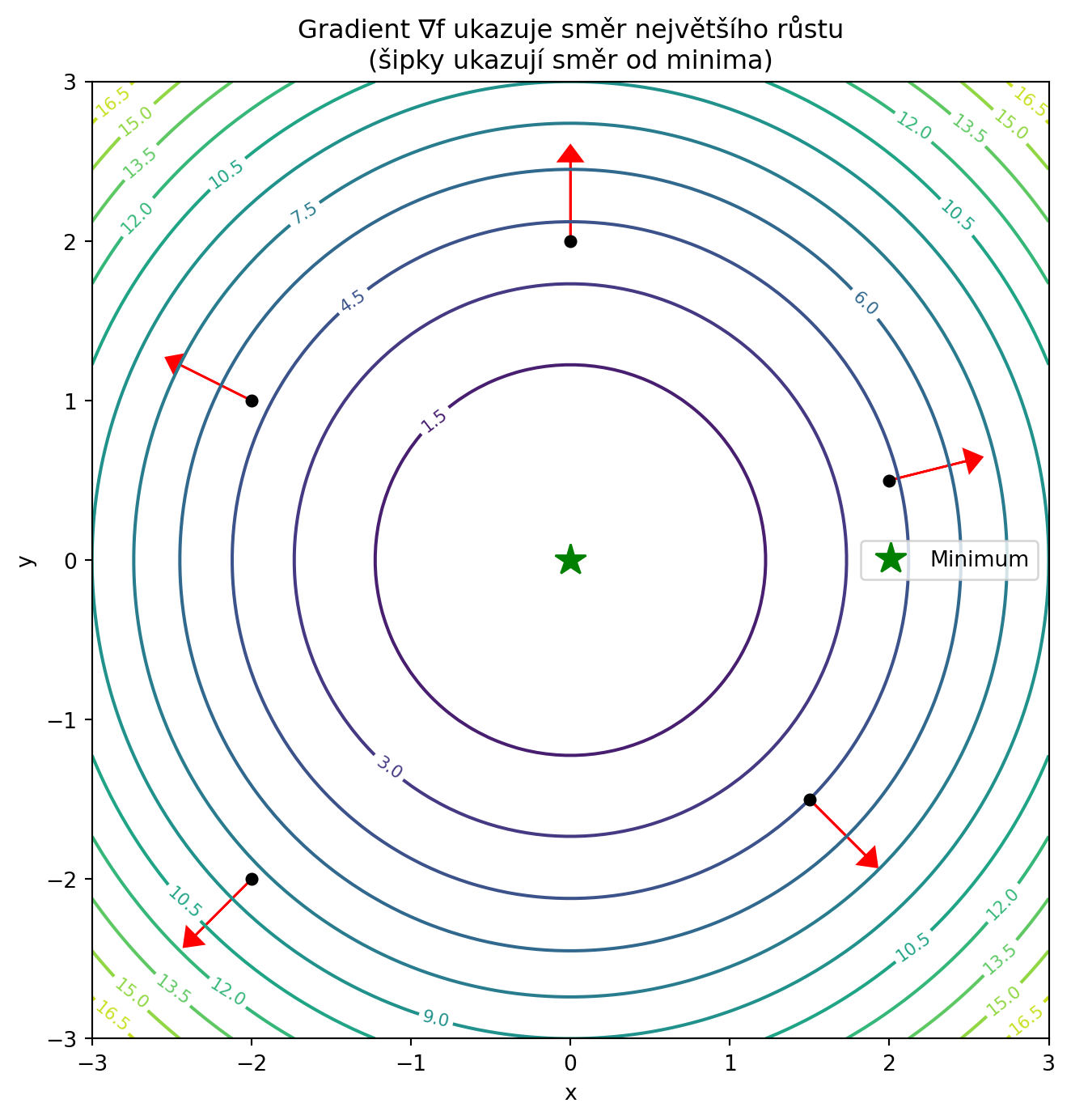
::: {.callout-warning title="Klíčová vlastnost!"}
Gradient ukazuje směr **největšího růstu** funkce. Záporný gradient ukazuje směr **největšího poklesu** -- přesně to, co potřebujeme pro minimalizaci loss!
:::
```{python}
# Příklad: gradient pro f(x,y) = x² + y²
from sympy import symbols, diff, Matrix
x, y = symbols('x y')
f = x**2 + y**2
gradient = Matrix([diff(f, x), diff(f, y)])
print(f"f(x, y) = {f}")
print(f"∇f = {gradient.T}") # Transpozice pro lepší zobrazení
```
### Vizualizace gradientu
```{python}
#| fig-cap: "Gradient ukazuje směr největšího růstu"
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return x**2 + y**2
def gradient_f(x, y):
return np.array([2*x, 2*y])
fig, ax = plt.subplots(figsize=(10, 8))
# Vrstevnice
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
contour = ax.contour(X, Y, Z, levels=15, cmap='viridis')
ax.clabel(contour, inline=True, fontsize=8)
# Gradienty v několika bodech
body = [(-2, -2), (-2, 1), (0, 2), (1.5, -1.5), (2, 0.5)]
for bx, by in body:
grad = gradient_f(bx, by)
# Normalizujeme pro lepší vizualizaci
grad_norm = grad / (np.linalg.norm(grad) + 0.001) * 0.5
ax.arrow(bx, by, grad_norm[0], grad_norm[1],
head_width=0.15, head_length=0.1, fc='red', ec='red')
ax.plot(bx, by, 'ko', markersize=5)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Gradient ∇f ukazuje směr největšího růstu\n(šipky ukazují směr od minima)')
ax.set_aspect('equal')
ax.plot(0, 0, 'g*', markersize=15, label='Minimum')
ax.legend()
plt.show()
```
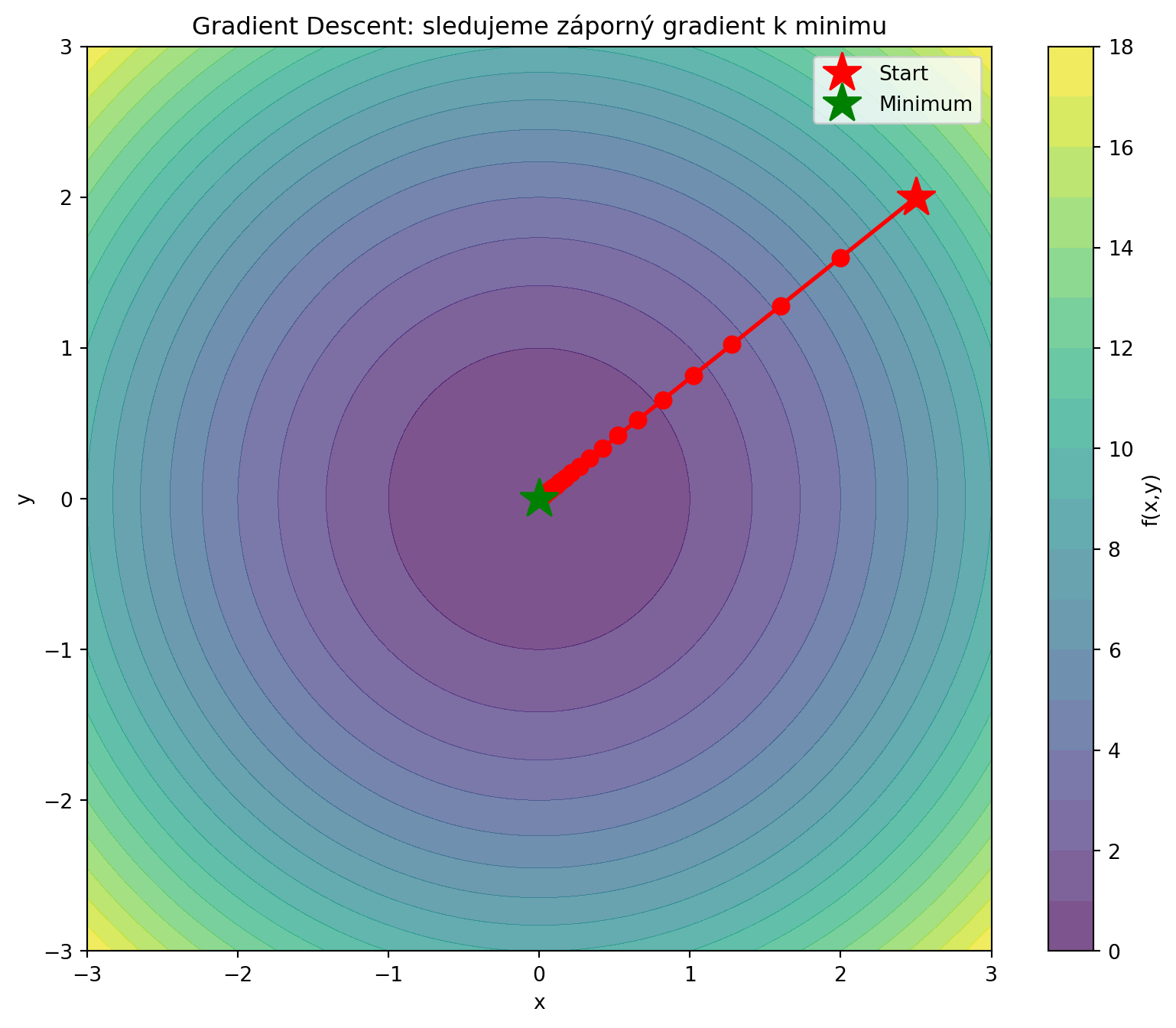
### Gradient Descent vizuálně
```{python}
#| fig-cap: "Gradient Descent na 2D funkci"
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return x**2 + y**2
def gradient_f(x, y):
return np.array([2*x, 2*y])
# Gradient descent
start = np.array([2.5, 2.0])
learning_rate = 0.1
pozice = [start.copy()]
for _ in range(20):
grad = gradient_f(pozice[-1][0], pozice[-1][1])
nova_pozice = pozice[-1] - learning_rate * grad
pozice.append(nova_pozice)
pozice = np.array(pozice)
# Vizualizace
fig, ax = plt.subplots(figsize=(10, 8))
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
contour = ax.contourf(X, Y, Z, levels=20, cmap='viridis', alpha=0.7)
plt.colorbar(contour, ax=ax, label='f(x,y)')
# Trajektorie
ax.plot(pozice[:, 0], pozice[:, 1], 'ro-', markersize=8, linewidth=2)
ax.plot(pozice[0, 0], pozice[0, 1], 'r*', markersize=20, label='Start')
ax.plot(0, 0, 'g*', markersize=20, label='Minimum')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Gradient Descent: sledujeme záporný gradient k minimu')
ax.legend()
ax.set_aspect('equal')
plt.show()
print("Trajektorie gradient descent:")
for i, pos in enumerate(pozice[:6]):
print(f"Krok {i}: ({pos[0]:.3f}, {pos[1]:.3f}), f = {f(pos[0], pos[1]):.4f}")
print("...")
print(f"Krok {len(pozice)-1}: ({pozice[-1][0]:.6f}, {pozice[-1][1]:.6f}), f = {f(pozice[-1][0], pozice[-1][1]):.8f}")
```
---
## Gradient v NumPy
```{python}
import numpy as np
def f(params):
"""Loss funkce s vektorem parametrů."""
x, y = params
return x**2 + y**2 + x*y
def gradient_f(params, h=1e-5):
"""Numerický gradient."""
grad = np.zeros_like(params)
for i in range(len(params)):
params_plus = params.copy()
params_plus[i] += h
params_minus = params.copy()
params_minus[i] -= h
grad[i] = (f(params_plus) - f(params_minus)) / (2 * h)
return grad
# Test
params = np.array([1.0, 2.0])
grad = gradient_f(params)
print(f"Parametry: {params}")
print(f"f(params) = {f(params)}")
print(f"Numerický gradient: {grad}")
# Analytický gradient pro srovnání: [2x + y, 2y + x]
print(f"Analytický gradient: [{2*params[0] + params[1]}, {2*params[1] + params[0]}]")
```
---
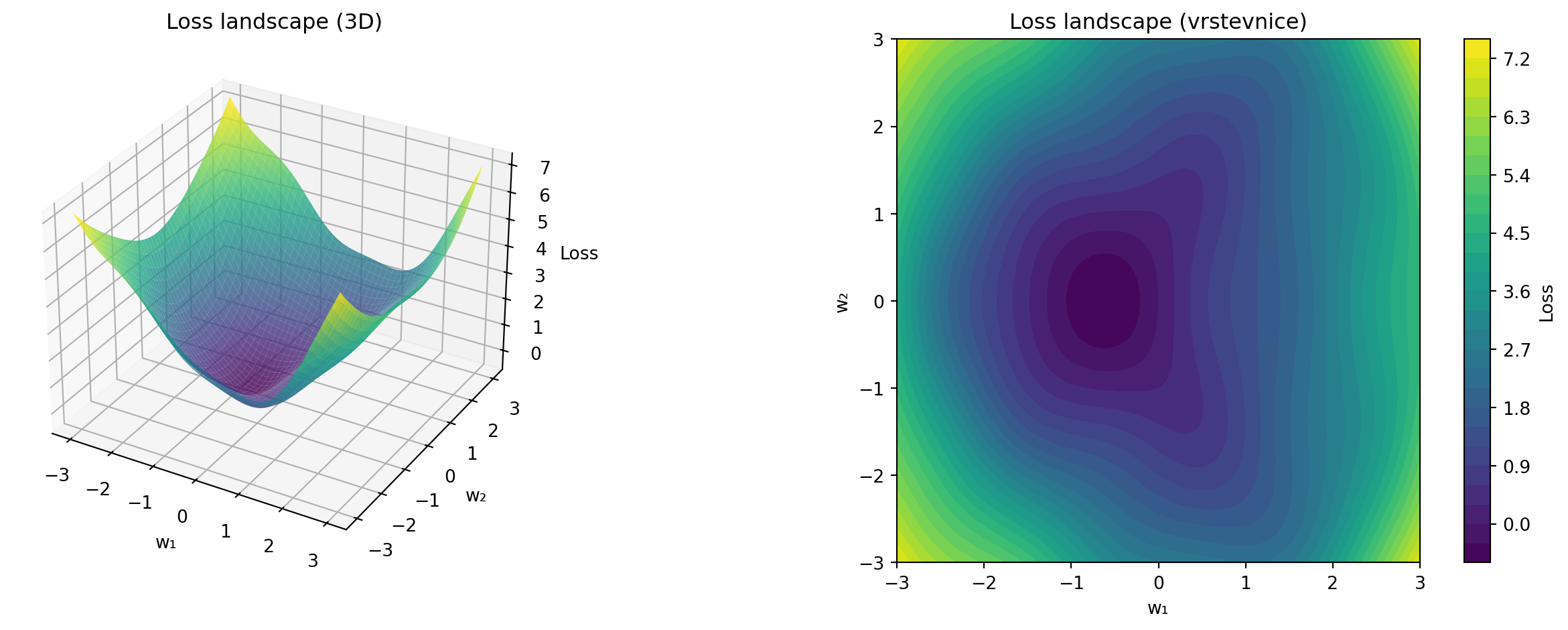
## Loss funkce neuronové sítě
V praxi máme loss funkci závislou na tisících parametrech:
$$\mathcal{L}(w_1, w_2, ..., w_n)$$
Gradient má stejný počet složek:
$$\nabla \mathcal{L} = \begin{bmatrix} \frac{\partial \mathcal{L}}{\partial w_1} \\ \frac{\partial \mathcal{L}}{\partial w_2} \\ \vdots \\ \frac{\partial \mathcal{L}}{\partial w_n} \end{bmatrix}$$
```{python}
#| fig-cap: "Loss landscape neuronové sítě (zjednodušeno na 2D)"
# Simulace složitější loss funkce
import numpy as np
import matplotlib.pyplot as plt
def loss(x, y):
return (np.sin(x) * np.cos(y) + 0.5 * x**2 + 0.3 * y**2
+ 0.2 * np.sin(3*x) * np.cos(2*y))
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)
Z = loss(X, Y)
fig = plt.figure(figsize=(14, 5))
# 3D pohled
ax1 = fig.add_subplot(121, projection='3d')
ax1.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
ax1.set_xlabel('w₁')
ax1.set_ylabel('w₂')
ax1.set_zlabel('Loss')
ax1.set_title('Loss landscape (3D)')
# Vrstevnice
ax2 = fig.add_subplot(122)
contour = ax2.contourf(X, Y, Z, levels=30, cmap='viridis')
plt.colorbar(contour, ax=ax2, label='Loss')
ax2.set_xlabel('w₁')
ax2.set_ylabel('w₂')
ax2.set_title('Loss landscape (vrstevnice)')
ax2.set_aspect('equal')
plt.tight_layout()
plt.show()
```
---
## Řešené příklady
### Příklad 1: Parciální derivace
Najděte parciální derivace $f(x, y) = x^3y + xy^2 - 5xy$
```{python}
from sympy import symbols, diff
x, y = symbols('x y')
f = x**3 * y + x * y**2 - 5*x*y
print(f"f(x, y) = {f}")
print(f"∂f/∂x = {diff(f, x)}")
print(f"∂f/∂y = {diff(f, y)}")
```
### Příklad 2: Gradient v bodě
Vypočítejte gradient funkce $f(x, y) = x^2 + 2xy + y^2$ v bodě $(1, 2)$.
```{python}
from sympy import symbols, diff, Matrix
x, y = symbols('x y')
f = x**2 + 2*x*y + y**2
df_dx = diff(f, x) # 2x + 2y
df_dy = diff(f, y) # 2x + 2y
print(f"f(x, y) = {f}")
print(f"∂f/∂x = {df_dx}")
print(f"∂f/∂y = {df_dy}")
# V bodě (1, 2)
grad_x = df_dx.subs([(x, 1), (y, 2)])
grad_y = df_dy.subs([(x, 1), (y, 2)])
print(f"\nGradient v bodě (1, 2): [{grad_x}, {grad_y}]")
```
### Příklad 3: Směr největšího růstu
V jakém směru roste funkce $f(x, y) = x^2 - y^2$ nejrychleji v bodě $(2, 1)$?
```{python}
# ∂f/∂x = 2x, ∂f/∂y = -2y
# V bodě (2, 1): gradient = [4, -2]
import numpy as np
gradient = np.array([4, -2])
smer = gradient / np.linalg.norm(gradient)
print(f"Gradient v (2, 1): {gradient}")
print(f"Směr největšího růstu: {smer.round(3)}")
print(f"Velikost gradientu: {np.linalg.norm(gradient):.3f}")
```
### Příklad 4: Gradient descent krok
Máme $f(x, y) = x^2 + 4y^2$, jsme v bodě $(3, 2)$, learning rate je $0.1$. Kam se posuneme?
```{python}
# Gradient: [2x, 8y]
import numpy as np
pozice = np.array([3.0, 2.0])
lr = 0.1
gradient = np.array([2 * pozice[0], 8 * pozice[1]])
nova_pozice = pozice - lr * gradient
print(f"Aktuální pozice: {pozice}")
print(f"Gradient: {gradient}")
print(f"Nová pozice: {nova_pozice}")
print(f"f před: {pozice[0]**2 + 4*pozice[1]**2}")
print(f"f po: {nova_pozice[0]**2 + 4*nova_pozice[1]**2}")
```
---
## Cvičení
::: {.callout-warning title="Cvičení 1: Parciální derivace"}
Najděte $\frac{\partial f}{\partial x}$ a $\frac{\partial f}{\partial y}$ pro $f(x,y) = 3x^2y - y^3 + 2x$
**Výsledky:** $6xy + 2$ a $3x^2 - 3y^2$
:::
::: {.callout-warning title="Cvičení 2: Gradient"}
Vypočítejte gradient $f(x, y) = e^{x+y}$ v bodě $(0, 0)$.
**Výsledek:** $[1, 1]$
<details>
<summary>Řešení</summary>
$\frac{\partial f}{\partial x} = e^{x+y}$, $\frac{\partial f}{\partial y} = e^{x+y}$
V $(0, 0)$: gradient = $[e^0, e^0] = [1, 1]$
</details>
:::
::: {.callout-warning title="Cvičení 3: Kritický bod"}
Najděte bod, kde je gradient funkce $f(x, y) = x^2 + y^2 - 2x - 4y$ nulový.
**Výsledek:** $(1, 2)$
<details>
<summary>Řešení</summary>
$\nabla f = [2x - 2, 2y - 4] = [0, 0]$
$x = 1$, $y = 2$
</details>
:::
::: {.callout-warning title="Cvičení 4: Gradient descent"}
Funkce $f(x, y) = x^2 + y^2$. Startujeme v $(4, 3)$ s learning rate $0.2$. Jaká je pozice po 2 krocích?
<details>
<summary>Řešení</summary>
Krok 1: $\nabla f = [8, 6]$, nová pozice: $(4 - 0.2 \cdot 8, 3 - 0.2 \cdot 6) = (2.4, 1.8)$
Krok 2: $\nabla f = [4.8, 3.6]$, nová pozice: $(2.4 - 0.96, 1.8 - 0.72) = (1.44, 1.08)$
</details>
:::
::: {.callout-warning title="Cvičení 5: Tří proměnné"}
Vypočítejte gradient $f(x, y, z) = x^2 + y^2 + z^2$.
**Výsledek:** $\nabla f = [2x, 2y, 2z]$
:::
---
## Shrnutí
::: {.callout-note title="Co si zapamatovat"}
- **Funkce více proměnných**: $f(x_1, x_2, ..., x_n) \rightarrow \mathbb{R}$
- **Parciální derivace** $\frac{\partial f}{\partial x_i}$: derivace podle jedné proměnné, ostatní konstantní
- **Gradient**: $\nabla f = [\frac{\partial f}{\partial x_1}, ..., \frac{\partial f}{\partial x_n}]$
- Gradient ukazuje **směr největšího růstu**
- **Gradient descent**: $\mathbf{x}_{new} = \mathbf{x}_{old} - \alpha \nabla f$
- V neuronových sítích gradient loss podle vah říká, jak je upravit
:::
V další kapitole se naučíme o **automatické derivaci** -- jak počítače počítají gradienty automaticky pomocí PyTorch.