# Pravidla derivování
::: {.callout-tip title="Co se naučíte"}
V této kapitole se naučíte:
- Pravidlo pro součet a rozdíl
- Pravidlo pro součin a podíl
- Řetízkové pravidlo (chain rule) - klíč k backpropagation
- Derivace složených funkcí
- Symbolické derivace pomocí SymPy
:::
## Proč potřebujeme pravidla?
V praxi se setkáváme se složitými funkcemi, které jsou kombinací jednoduchých. Potřebujeme pravidla, jak derivovat:
- Součet funkcí: $f(x) + g(x)$
- Součin funkcí: $f(x) \cdot g(x)$
- Složené funkce: $f(g(x))$
Tato pravidla jsou základem **backpropagation** v neuronových sítích!
---
## Pravidlo pro konstantní násobek
$$(c \cdot f(x))' = c \cdot f'(x)$$
Konstanta "projde" derivací beze změny.
```{python}
import numpy as np
import matplotlib.pyplot as plt
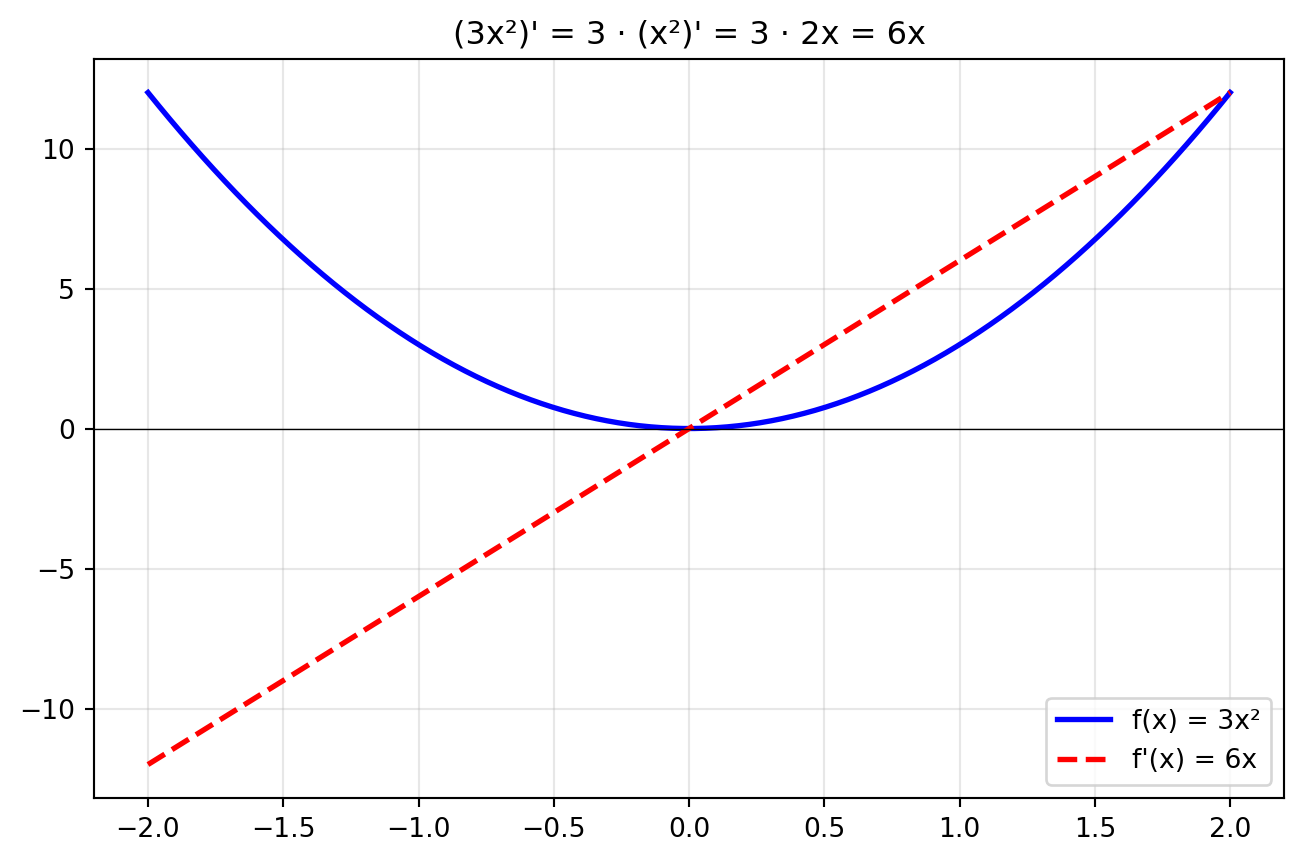
# Příklad: derivace 3x²
# (3x²)' = 3 · (x²)' = 3 · 2x = 6x
def f(x):
return 3 * x**2
def f_derivace(x):
return 6 * x
x = np.linspace(-2, 2, 100)
fig, ax = plt.subplots(figsize=(8, 5))
ax.plot(x, f(x), 'b-', linewidth=2, label='f(x) = 3x²')
ax.plot(x, f_derivace(x), 'r--', linewidth=2, label="f'(x) = 6x")
ax.legend()
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='k', linewidth=0.5)
ax.set_title("(3x²)' = 3 · (x²)' = 3 · 2x = 6x")
plt.show()
```
---
## Pravidlo pro součet a rozdíl
$$(f(x) + g(x))' = f'(x) + g'(x)$$
$$(f(x) - g(x))' = f'(x) - g'(x)$$
Derivace součtu je součet derivací.
```{python}
# Příklad: (x² + 3x)' = (x²)' + (3x)' = 2x + 3
def f(x):
return x**2 + 3*x
def f_derivace(x):
return 2*x + 3
# Ověření numericky
x = 2
h = 0.0001
numericka = (f(x + h) - f(x)) / h
analyticka = f_derivace(x)
print("f(x) = x² + 3x")
print("f'(x) = 2x + 3")
print(f"\nf'(2):")
print(f" Analyticky: 2·2 + 3 = {analyticka}")
print(f" Numericky: {numericka:.4f}")
```
---
## Pravidlo pro součin
$$(f(x) \cdot g(x))' = f'(x) \cdot g(x) + f(x) \cdot g'(x)$$
::: {.callout-note title="Pamatovačka"}
"Derivace prvního krát druhá PLUS první krát derivace druhé"
:::
```{python}
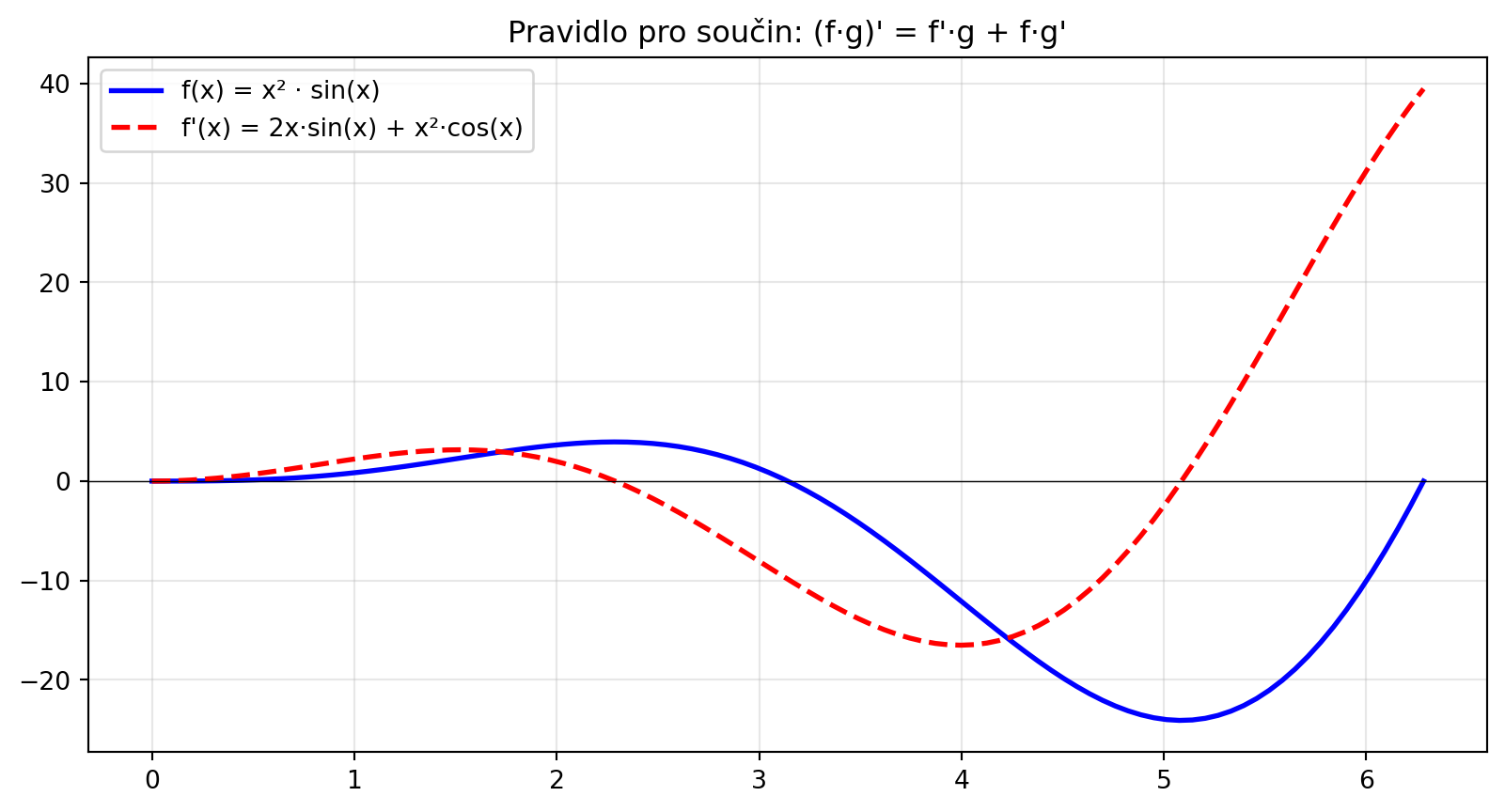
# Příklad: (x² · sin(x))'
# = (x²)' · sin(x) + x² · (sin(x))'
# = 2x · sin(x) + x² · cos(x)
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**2 * np.sin(x)
def f_derivace(x):
return 2*x * np.sin(x) + x**2 * np.cos(x)
x = np.linspace(0, 2*np.pi, 100)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, f(x), 'b-', linewidth=2, label='f(x) = x² · sin(x)')
ax.plot(x, f_derivace(x), 'r--', linewidth=2, label="f'(x) = 2x·sin(x) + x²·cos(x)")
ax.legend()
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='k', linewidth=0.5)
ax.set_title("Pravidlo pro součin: (f·g)' = f'·g + f·g'")
plt.show()
```
---
## Pravidlo pro podíl
$$\left(\frac{f(x)}{g(x)}\right)' = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{(g(x))^2}$$
::: {.callout-note title="Pamatovačka"}
"Derivace čitatele krát jmenovatel MINUS čitatel krát derivace jmenovatele, to celé děleno jmenovatelem na druhou"
:::
```{python}
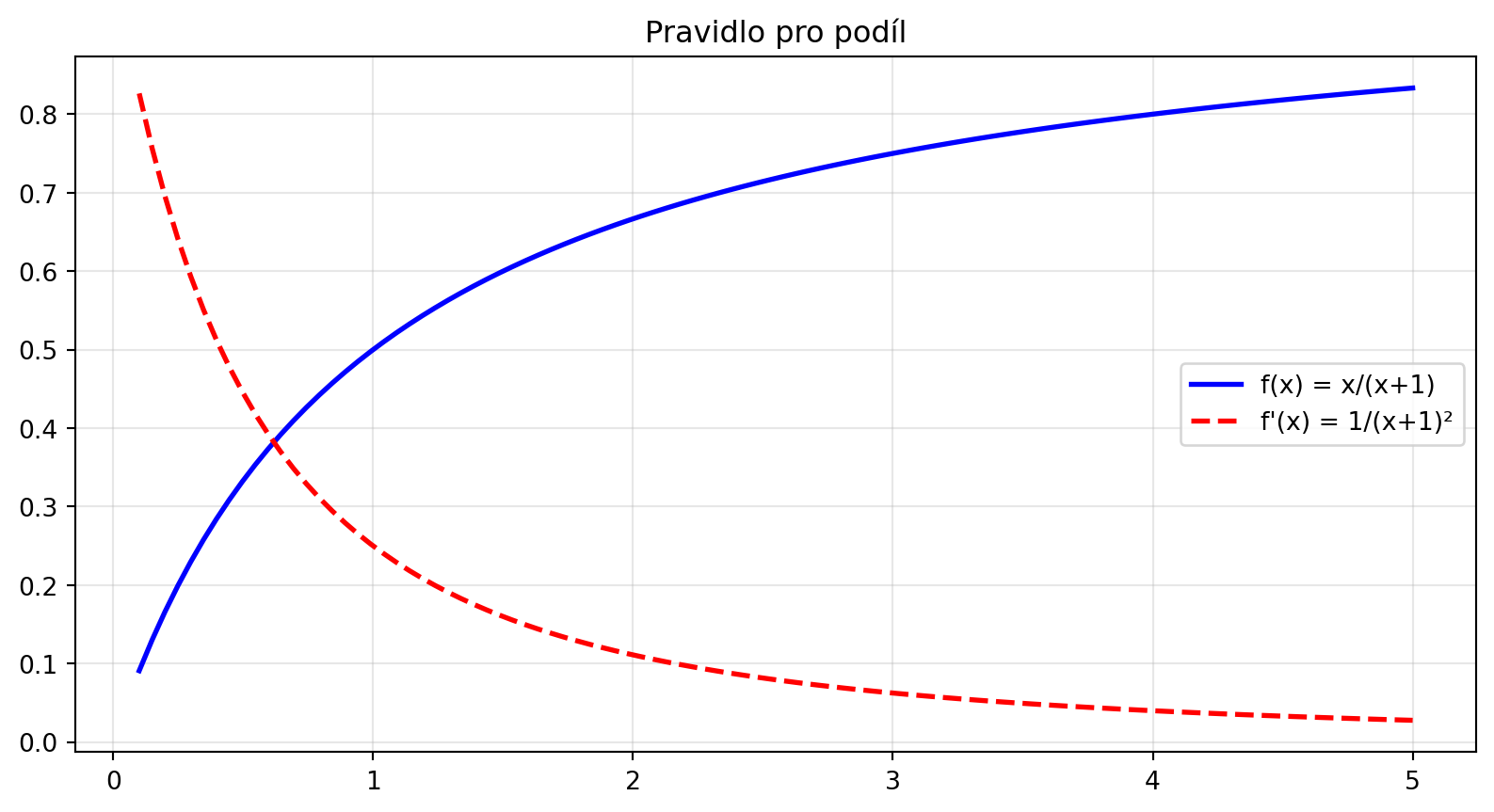
# Příklad: (x / (x+1))'
# f = x, f' = 1
# g = x+1, g' = 1
# = (1·(x+1) - x·1) / (x+1)² = (x+1-x) / (x+1)² = 1 / (x+1)²
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x / (x + 1)
def f_derivace(x):
return 1 / (x + 1)**2
x = np.linspace(0.1, 5, 100)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, f(x), 'b-', linewidth=2, label='f(x) = x/(x+1)')
ax.plot(x, f_derivace(x), 'r--', linewidth=2, label="f'(x) = 1/(x+1)²")
ax.legend()
ax.grid(True, alpha=0.3)
ax.set_title("Pravidlo pro podíl")
plt.show()
```
---
## Řetízkové pravidlo (Chain Rule)
**Řetízkové pravidlo** je nejdůležitější pravidlo pro strojové učení. Říká nám, jak derivovat složenou funkci $f(g(x))$:
$$(f(g(x)))' = f'(g(x)) \cdot g'(x)$$
Nebo v Leibnizově notaci:
$$\frac{df}{dx} = \frac{df}{dg} \cdot \frac{dg}{dx}$$
::: {.callout-warning title="Proč je to klíčové?"}
**Backpropagation** v neuronových sítích je opakované použití řetízkového pravidla! Gradient se "řetězí" zpět přes všechny vrstvy.
:::
### Příklad: Složená funkce
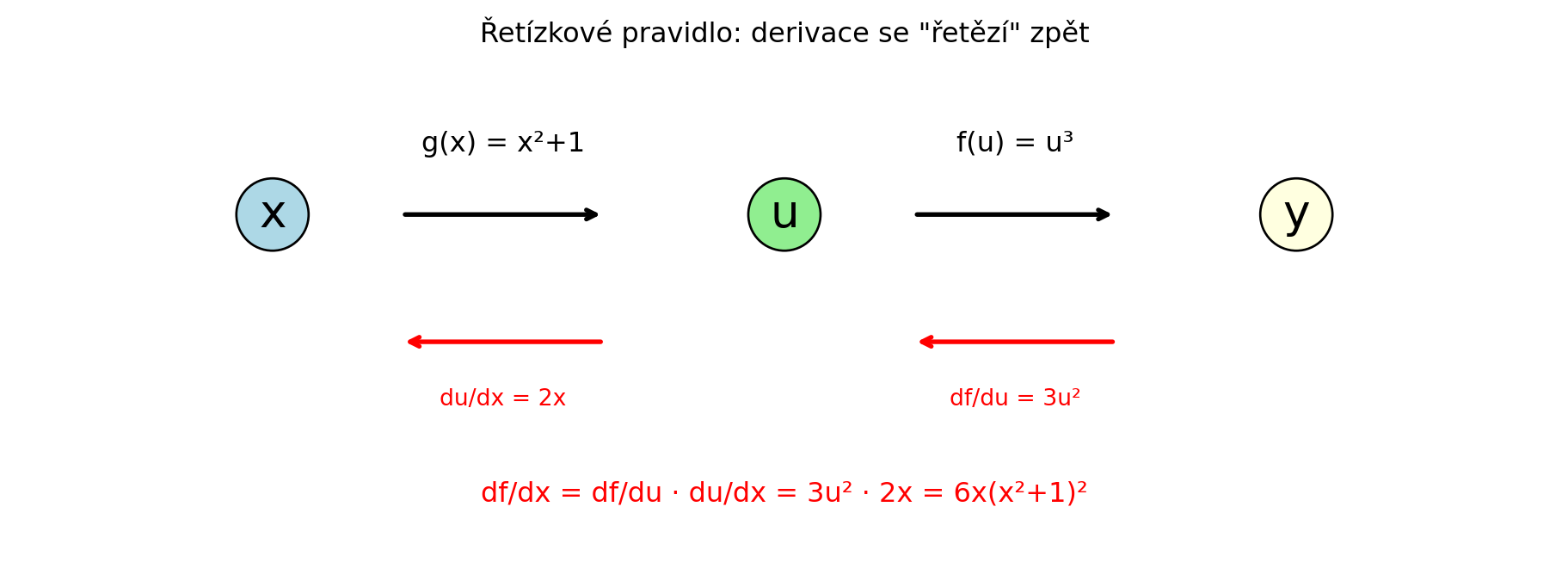
Derivujme $f(x) = (x^2 + 1)^3$
- Vnější funkce: $h(u) = u^3$ → $h'(u) = 3u^2$
- Vnitřní funkce: $u(x) = x^2 + 1$ → $u'(x) = 2x$
$$f'(x) = 3(x^2 + 1)^2 \cdot 2x = 6x(x^2 + 1)^2$$
```{python}
def f(x):
return (x**2 + 1)**3
def f_derivace(x):
return 6 * x * (x**2 + 1)**2
# Ověření
x = 2
h = 0.0001
numericka = (f(x + h) - f(x)) / h
analyticka = f_derivace(x)
print("f(x) = (x² + 1)³")
print("f'(x) = 6x(x² + 1)²")
print(f"\nf'(2):")
print(f" Analyticky: 6·2·(4+1)² = 12·25 = {analyticka}")
print(f" Numericky: {numericka:.2f}")
```
```{python}
#| fig-cap: "Vizualizace řetízkového pravidla"
#| code-fold: true
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12, 4))
# Graf řetězce
ax.text(1, 0.5, 'x', fontsize=20, ha='center', va='center',
bbox=dict(boxstyle='circle', facecolor='lightblue'))
ax.annotate('', xy=(2.3, 0.5), xytext=(1.5, 0.5),
arrowprops=dict(arrowstyle='->', lw=2))
ax.text(1.9, 0.7, 'g(x) = x²+1', fontsize=12, ha='center')
ax.text(3, 0.5, 'u', fontsize=20, ha='center', va='center',
bbox=dict(boxstyle='circle', facecolor='lightgreen'))
ax.annotate('', xy=(4.3, 0.5), xytext=(3.5, 0.5),
arrowprops=dict(arrowstyle='->', lw=2))
ax.text(3.9, 0.7, 'f(u) = u³', fontsize=12, ha='center')
ax.text(5, 0.5, 'y', fontsize=20, ha='center', va='center',
bbox=dict(boxstyle='circle', facecolor='lightyellow'))
# Zpětný tok (derivace)
ax.annotate('', xy=(3.5, 0.1), xytext=(4.3, 0.1),
arrowprops=dict(arrowstyle='->', color='red', lw=2))
ax.text(3.9, -0.1, "df/du = 3u²", fontsize=10, ha='center', color='red')
ax.annotate('', xy=(1.5, 0.1), xytext=(2.3, 0.1),
arrowprops=dict(arrowstyle='->', color='red', lw=2))
ax.text(1.9, -0.1, "du/dx = 2x", fontsize=10, ha='center', color='red')
ax.text(3, -0.4, "df/dx = df/du · du/dx = 3u² · 2x = 6x(x²+1)²",
fontsize=12, ha='center', color='red')
ax.set_xlim(0, 6)
ax.set_ylim(-0.6, 1)
ax.axis('off')
ax.set_title('Řetízkové pravidlo: derivace se "řetězí" zpět')
plt.show()
```
### Více vrstev řetězení
Pro $f(g(h(x)))$:
$$\frac{df}{dx} = \frac{df}{dg} \cdot \frac{dg}{dh} \cdot \frac{dh}{dx}$$
```{python}
# f(x) = sin(exp(x²))
# h(x) = x², h'(x) = 2x
# g(u) = exp(u), g'(u) = exp(u)
# f(v) = sin(v), f'(v) = cos(v)
# f'(x) = cos(exp(x²)) · exp(x²) · 2x
import numpy as np
def f(x):
return np.sin(np.exp(x**2))
def f_derivace(x):
return np.cos(np.exp(x**2)) * np.exp(x**2) * 2*x
x = 0.5
h = 0.00001
numericka = (f(x + h) - f(x)) / h
analyticka = f_derivace(x)
print("f(x) = sin(exp(x²))")
print("f'(x) = cos(exp(x²)) · exp(x²) · 2x")
print(f"\nf'(0.5):")
print(f" Analyticky: {analyticka:.6f}")
print(f" Numericky: {numericka:.6f}")
```
---
## Aplikace: Backpropagation
V neuronové síti máme řetězec operací:
$$\text{input} \xrightarrow{W_1} h_1 \xrightarrow{\sigma} a_1 \xrightarrow{W_2} h_2 \xrightarrow{\sigma} \text{output} \rightarrow \text{Loss}$$
Gradient loss podle $W_1$ vypočítáme řetízkovým pravidlem:
$$\frac{\partial \text{Loss}}{\partial W_1} = \frac{\partial \text{Loss}}{\partial \text{output}} \cdot \frac{\partial \text{output}}{\partial a_1} \cdot \frac{\partial a_1}{\partial h_1} \cdot \frac{\partial h_1}{\partial W_1}$$
```{python}
#| fig-cap: "Backpropagation = řetízkové pravidlo"
#| code-fold: true
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(14, 5))
# Forward pass (nahoře)
nodes = ['x', 'W₁x', 'σ(·)', 'W₂·', 'σ(·)', 'Loss']
x_pos = [1, 2.5, 4, 5.5, 7, 8.5]
for i, (node, x) in enumerate(zip(nodes, x_pos)):
color = 'lightblue' if i < len(nodes)-1 else 'lightyellow'
ax.add_patch(plt.Rectangle((x-0.4, 0.6), 0.8, 0.6, facecolor=color, edgecolor='blue'))
ax.text(x, 0.9, node, ha='center', va='center', fontsize=11)
if i < len(nodes)-1:
ax.annotate('', xy=(x_pos[i+1]-0.4, 0.9), xytext=(x+0.4, 0.9),
arrowprops=dict(arrowstyle='->', color='blue', lw=1.5))
ax.text(5, 1.4, 'Forward pass →', fontsize=12, ha='center', color='blue')
# Backward pass (dole)
for i in range(len(nodes)-1, 0, -1):
ax.annotate('', xy=(x_pos[i-1]+0.4, 0.3), xytext=(x_pos[i]-0.4, 0.3),
arrowprops=dict(arrowstyle='->', color='red', lw=1.5))
ax.text(5, 0.1, '← Backward pass (gradients)', fontsize=12, ha='center', color='red')
# Rovnice
ax.text(5, -0.3, r'$\frac{\partial Loss}{\partial W_1} = \frac{\partial Loss}{\partial out} \cdot \frac{\partial out}{\partial h_2} \cdot \frac{\partial h_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial h_1} \cdot \frac{\partial h_1}{\partial W_1}$',
fontsize=12, ha='center')
ax.set_xlim(0, 10)
ax.set_ylim(-0.5, 1.6)
ax.axis('off')
ax.set_title('Backpropagation: opakované použití řetízkového pravidla')
plt.show()
```
---
## Symbolické derivace s SymPy
Pro složité výrazy můžeme použít symbolickou matematiku:
```{python}
from sympy import symbols, diff, sin, cos, exp, sqrt, simplify
x = symbols('x')
# Definujeme funkci
f = (x**2 + 1)**3
# Derivujeme
f_prime = diff(f, x)
print(f"f(x) = {f}")
print(f"f'(x) = {f_prime}")
print(f"f'(x) zjednodušeno = {simplify(f_prime)}")
```
```{python}
# Složitější příklady
priklady = [
x**5 - 3*x**2 + 2*x - 7,
sin(x) * cos(x),
exp(x**2),
x / (x**2 + 1),
sqrt(x**2 + 1)
]
print("Symbolické derivace:")
print("-" * 50)
for expr in priklady:
deriv = diff(expr, x)
print(f"f(x) = {expr}")
print(f"f'(x) = {simplify(deriv)}")
print()
```
### Vyhodnocení v bodě
```{python}
from sympy import symbols, diff, lambdify
import numpy as np
x = symbols('x')
f = x**3 - 2*x**2 + x
# Derivace
f_prime = diff(f, x)
# Převedeme na Python funkci
f_num = lambdify(x, f, 'numpy')
f_prime_num = lambdify(x, f_prime, 'numpy')
print(f"f(x) = {f}")
print(f"f'(x) = {f_prime}")
# Vyhodnotíme
bod = 2
print(f"\nf({bod}) = {f_num(bod)}")
print(f"f'({bod}) = {f_prime_num(bod)}")
```
---
## Tabulka derivací
| Funkce $f(x)$ | Derivace $f'(x)$ |
|---------------|------------------|
| $c$ | $0$ |
| $x^n$ | $n x^{n-1}$ |
| $e^x$ | $e^x$ |
| $a^x$ | $a^x \ln(a)$ |
| $\ln(x)$ | $\frac{1}{x}$ |
| $\log_a(x)$ | $\frac{1}{x \ln(a)}$ |
| $\sin(x)$ | $\cos(x)$ |
| $\cos(x)$ | $-\sin(x)$ |
| $\tan(x)$ | $\frac{1}{\cos^2(x)}$ |
---
## Řešené příklady
### Příklad 1: Součet
Derivujte $f(x) = x^4 - 3x^2 + 5x - 2$
```{python}
from sympy import symbols, diff
x = symbols('x')
f = x**4 - 3*x**2 + 5*x - 2
f_prime = diff(f, x)
print(f"f(x) = {f}")
print(f"f'(x) = {f_prime}")
print("\nPostup:")
print("(x⁴)' = 4x³")
print("(-3x²)' = -6x")
print("(5x)' = 5")
print("(-2)' = 0")
print("Součet: 4x³ - 6x + 5")
```
### Příklad 2: Součin
Derivujte $f(x) = x^2 \cdot e^x$
```{python}
from sympy import symbols, diff, exp
x = symbols('x')
f = x**2 * exp(x)
f_prime = diff(f, x)
print(f"f(x) = {f}")
print(f"f'(x) = {f_prime}")
print("\nPostup (pravidlo pro součin):")
print("f' = (x²)' · eˣ + x² · (eˣ)'")
print("f' = 2x · eˣ + x² · eˣ")
print("f' = eˣ(2x + x²) = eˣ(x² + 2x)")
```
### Příklad 3: Podíl
Derivujte $f(x) = \frac{x^2}{x + 1}$
```{python}
from sympy import symbols, diff, simplify
x = symbols('x')
f = x**2 / (x + 1)
f_prime = diff(f, x)
print(f"f(x) = {f}")
print(f"f'(x) = {simplify(f_prime)}")
print("\nPostup (pravidlo pro podíl):")
print("f' = [(x²)'·(x+1) - x²·(x+1)'] / (x+1)²")
print("f' = [2x·(x+1) - x²·1] / (x+1)²")
print("f' = [2x² + 2x - x²] / (x+1)²")
print("f' = (x² + 2x) / (x+1)²")
```
### Příklad 4: Řetízkové pravidlo
Derivujte $f(x) = \sin(x^2)$
```{python}
from sympy import symbols, diff, sin, cos
x = symbols('x')
f = sin(x**2)
f_prime = diff(f, x)
print(f"f(x) = {f}")
print(f"f'(x) = {f_prime}")
print("\nPostup (řetízkové pravidlo):")
print("Vnější: sin(u), derivace: cos(u)")
print("Vnitřní: u = x², derivace: 2x")
print("f'(x) = cos(x²) · 2x = 2x·cos(x²)")
```
### Příklad 5: Více vrstev
Derivujte $f(x) = e^{\sin(x)}$
```{python}
from sympy import symbols, diff, sin, exp
x = symbols('x')
f = exp(sin(x))
f_prime = diff(f, x)
print(f"f(x) = {f}")
print(f"f'(x) = {f_prime}")
print("\nPostup:")
print("Vnější: eᵘ, derivace: eᵘ")
print("Vnitřní: u = sin(x), derivace: cos(x)")
print("f'(x) = eˢⁱⁿ⁽ˣ⁾ · cos(x)")
```
---
## Cvičení
::: {.callout-warning title="Cvičení 1: Součet"}
Derivujte $f(x) = 3x^5 - 2x^3 + x - 7$
**Výsledek:** $f'(x) = 15x^4 - 6x^2 + 1$
:::
::: {.callout-warning title="Cvičení 2: Součin"}
Derivujte $f(x) = x \cdot \ln(x)$
**Výsledek:** $f'(x) = \ln(x) + 1$
<details>
<summary>Řešení</summary>
$(x)' \cdot \ln(x) + x \cdot (\ln(x))' = 1 \cdot \ln(x) + x \cdot \frac{1}{x} = \ln(x) + 1$
</details>
:::
::: {.callout-warning title="Cvičení 3: Řetízkové pravidlo"}
Derivujte $f(x) = (2x + 1)^4$
**Výsledek:** $f'(x) = 8(2x + 1)^3$
<details>
<summary>Řešení</summary>
Vnější: $u^4$, derivace: $4u^3$
Vnitřní: $u = 2x + 1$, derivace: $2$
$f'(x) = 4(2x+1)^3 \cdot 2 = 8(2x+1)^3$
</details>
:::
::: {.callout-warning title="Cvičení 4: Složená funkce"}
Derivujte $f(x) = \sqrt{x^2 + 1}$
**Výsledek:** $f'(x) = \frac{x}{\sqrt{x^2 + 1}}$
<details>
<summary>Řešení</summary>
$f(x) = (x^2 + 1)^{1/2}$
$f'(x) = \frac{1}{2}(x^2+1)^{-1/2} \cdot 2x = \frac{x}{\sqrt{x^2+1}}$
</details>
:::
::: {.callout-warning title="Cvičení 5: SymPy"}
Použijte SymPy k derivaci $f(x) = \frac{\sin(x)}{x}$
<details>
<summary>Řešení</summary>
```python
from sympy import symbols, diff, sin, simplify
x = symbols('x')
f = sin(x) / x
print(simplify(diff(f, x)))
# Výsledek: (x*cos(x) - sin(x))/x²
```
</details>
:::
::: {.callout-warning title="Cvičení 6: Aktivační funkce"}
Derivujte sigmoid: $\sigma(x) = \frac{1}{1 + e^{-x}}$
**Výsledek:** $\sigma'(x) = \sigma(x)(1 - \sigma(x))$
<details>
<summary>Řešení</summary>
Toto je slavná vlastnost sigmoidu - jeho derivace se dá vyjádřit pomocí něj samého!
</details>
:::
---
## Shrnutí
::: {.callout-note title="Co si zapamatovat"}
- **Konstantní násobek:** $(cf)' = c \cdot f'$
- **Součet:** $(f + g)' = f' + g'$
- **Součin:** $(fg)' = f'g + fg'$
- **Podíl:** $(f/g)' = (f'g - fg')/g^2$
- **Řetízkové pravidlo:** $(f(g(x)))' = f'(g(x)) \cdot g'(x)$
- Řetízkové pravidlo = **základ backpropagation**
- **SymPy** umí symbolicky derivovat
:::
V další kapitole rozšíříme derivace na **funkce více proměnných** -- parciální derivace a gradient.