# Lineární funkce
::: {.callout-tip title="Co se naučíte"}
V této kapitole se naučíte:
- Co je lineární funkce a jak vypadá její graf
- Co znamená směrnice a úsek na ose y
- Jak najít průsečíky přímek
- Jak použít lineární funkce pro predikce
- Základy lineární regrese v Pythonu
:::
## Co je lineární funkce?
**Lineární funkce** je funkce tvaru:
$$f(x) = ax + b$$
kde:
- **a** je **směrnice** (sklon přímky)
- **b** je **úsek na ose y** (kde přímka protíná osu y)
Grafem lineární funkce je vždy **přímka**.
```{python}
#| fig-cap: "Různé lineární funkce"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
plt.figure(figsize=(10, 6))
# Různé lineární funkce
plt.plot(x, 2*x + 1, label='f(x) = 2x + 1', linewidth=2)
plt.plot(x, 0.5*x - 1, label='f(x) = 0.5x - 1', linewidth=2)
plt.plot(x, -x + 2, label='f(x) = -x + 2', linewidth=2)
plt.plot(x, 0*x + 1.5, label='f(x) = 1.5 (konstantní)', linewidth=2, linestyle='--')
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Příklady lineárních funkcí')
plt.legend()
plt.ylim(-5, 7)
plt.show()
```
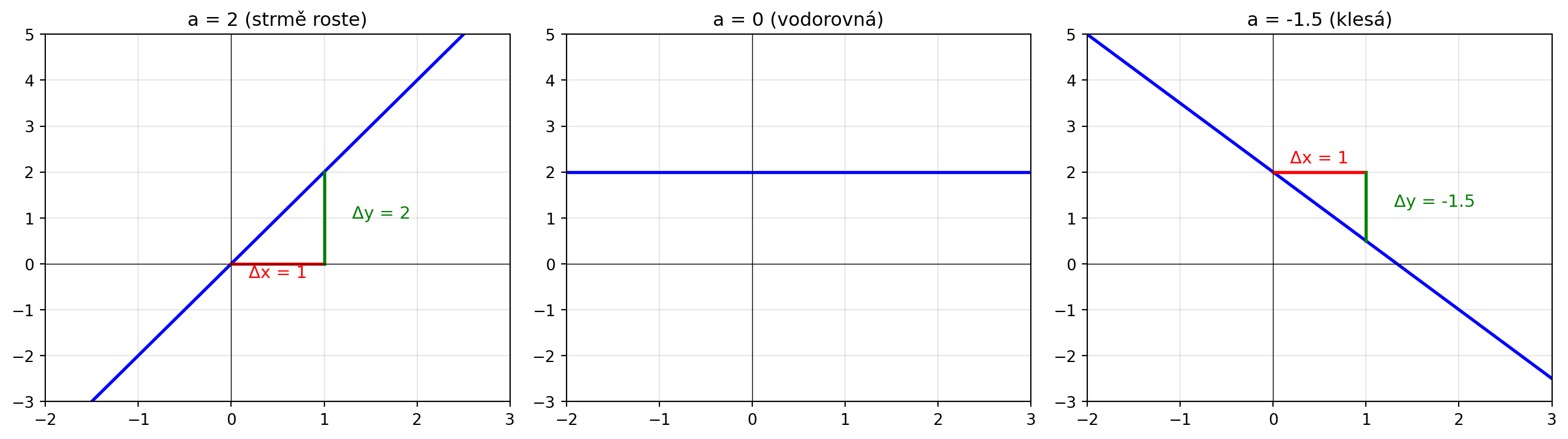
## Směrnice -- sklon přímky
**Směrnice** (značíme *a* nebo *k*) určuje, jak rychle funkce roste nebo klesá.
$$\text{směrnice} = \frac{\text{změna y}}{\text{změna x}} = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1}$$
```{python}
#| fig-cap: "Směrnice přímky"
#| code-fold: true
import numpy as np
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 3, figsize=(14, 4))
x = np.linspace(-2, 3, 100)
# Kladná směrnice
axes[0].plot(x, 2*x, 'b-', linewidth=2)
axes[0].plot([0, 1], [0, 0], 'r-', linewidth=2)
axes[0].plot([1, 1], [0, 2], 'g-', linewidth=2)
axes[0].annotate('Δx = 1', xy=(0.5, -0.3), fontsize=11, color='red', ha='center')
axes[0].annotate('Δy = 2', xy=(1.3, 1), fontsize=11, color='green')
axes[0].set_title('a = 2 (strmě roste)', fontsize=12)
axes[0].grid(True, alpha=0.3)
axes[0].set_xlim(-2, 3)
axes[0].set_ylim(-3, 5)
axes[0].axhline(y=0, color='k', linewidth=0.5)
axes[0].axvline(x=0, color='k', linewidth=0.5)
# Nulová směrnice
axes[1].plot(x, 0*x + 2, 'b-', linewidth=2)
axes[1].set_title('a = 0 (vodorovná)', fontsize=12)
axes[1].grid(True, alpha=0.3)
axes[1].set_xlim(-2, 3)
axes[1].set_ylim(-3, 5)
axes[1].axhline(y=0, color='k', linewidth=0.5)
axes[1].axvline(x=0, color='k', linewidth=0.5)
# Záporná směrnice
axes[2].plot(x, -1.5*x + 2, 'b-', linewidth=2)
axes[2].plot([0, 1], [2, 2], 'r-', linewidth=2)
axes[2].plot([1, 1], [2, 0.5], 'g-', linewidth=2)
axes[2].annotate('Δx = 1', xy=(0.5, 2.2), fontsize=11, color='red', ha='center')
axes[2].annotate('Δy = -1.5', xy=(1.3, 1.25), fontsize=11, color='green')
axes[2].set_title('a = -1.5 (klesá)', fontsize=12)
axes[2].grid(True, alpha=0.3)
axes[2].set_xlim(-2, 3)
axes[2].set_ylim(-3, 5)
axes[2].axhline(y=0, color='k', linewidth=0.5)
axes[2].axvline(x=0, color='k', linewidth=0.5)
plt.tight_layout()
plt.show()
```
::: {.callout-note title="Význam směrnice"}
| Směrnice | Význam |
|----------|--------|
| a > 0 | Přímka roste (zleva doprava nahoru) |
| a = 0 | Přímka je vodorovná (konstantní funkce) |
| a < 0 | Přímka klesá (zleva doprava dolů) |
| \|a\| velké | Strmá přímka |
| \|a\| malé | Mírná přímka |
:::
### Výpočet směrnice ze dvou bodů
```{python}
def smernice(bod1, bod2):
"""Vypočítá směrnici přímky procházející dvěma body."""
x1, y1 = bod1
x2, y2 = bod2
return (y2 - y1) / (x2 - x1)
# Příklad: přímka prochází body [1, 3] a [4, 9]
A = [1, 3]
B = [4, 9]
a = smernice(A, B)
print(f"Směrnice přímky AB: {a}")
print(f"Ověření: (9-3)/(4-1) = 6/3 = {6/3}")
```
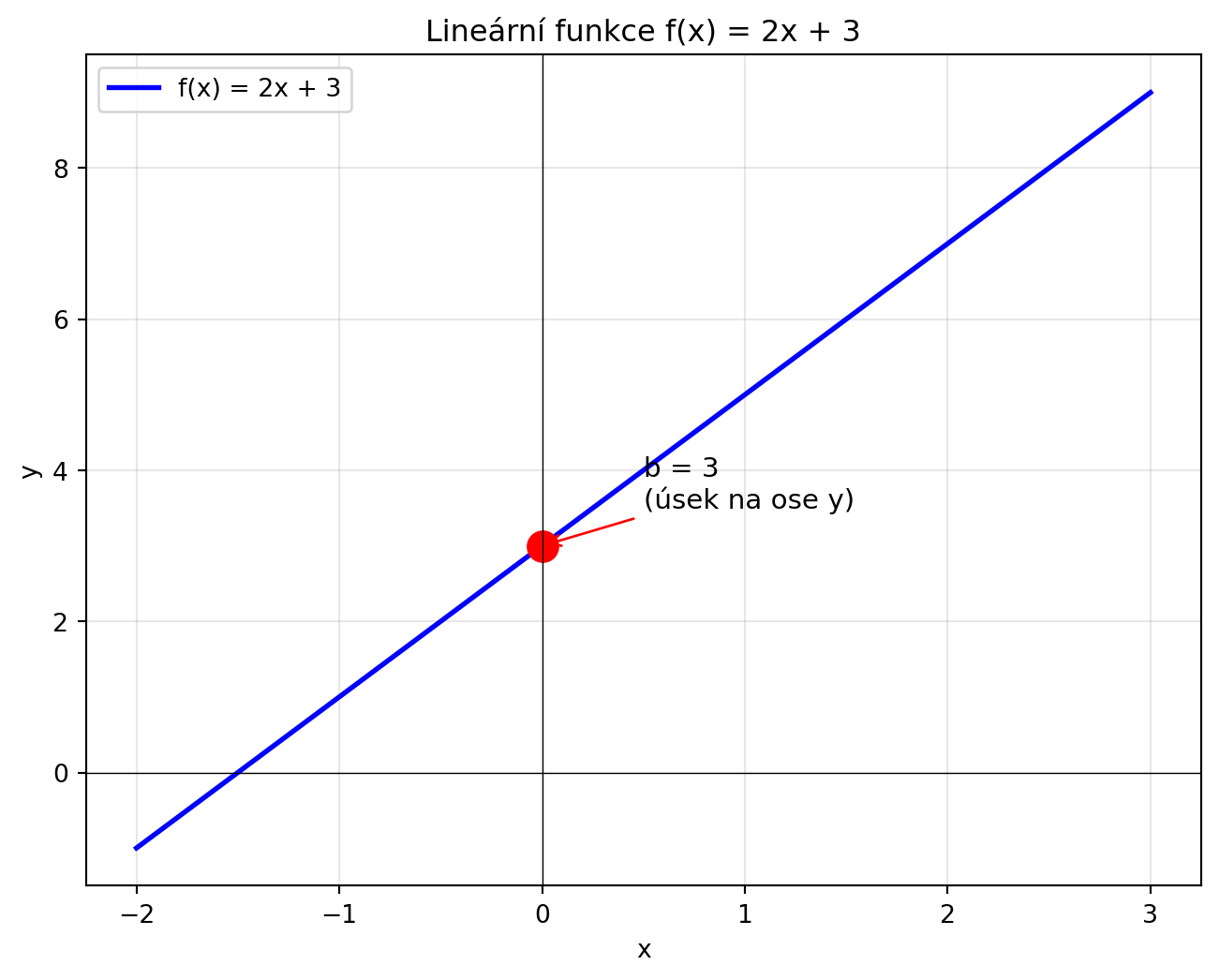
## Úsek na ose y
**Úsek na ose y** (značíme *b* nebo *q*) je hodnota y, když x = 0. Je to bod, kde přímka protíná svislou osu.
```{python}
#| fig-cap: "Úsek na ose y"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 3, 100)
plt.figure(figsize=(8, 6))
plt.plot(x, 2*x + 3, 'b-', linewidth=2, label='f(x) = 2x + 3')
# Zvýraznění úseku na ose y
plt.plot(0, 3, 'ro', markersize=12)
plt.annotate('b = 3\n(úsek na ose y)', xy=(0, 3), xytext=(0.5, 3.5),
fontsize=11, arrowprops=dict(arrowstyle='->', color='red'))
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Lineární funkce f(x) = 2x + 3')
plt.legend()
plt.show()
```
## Rovnice přímky z různých údajů
### Ze směrnice a bodu
Známe-li směrnici *a* a bod $[x_0, y_0]$, kterým přímka prochází:
$$y - y_0 = a(x - x_0)$$
```{python}
def primka_ze_smernice_a_bodu(a, bod):
"""Vrátí rovnici přímky ve tvaru y = ax + b."""
x0, y0 = bod
b = y0 - a * x0
return a, b
# Přímka se směrnicí 2 procházející bodem [3, 5]
a, b = primka_ze_smernice_a_bodu(2, [3, 5])
print(f"Rovnice přímky: y = {a}x + {b}")
print(f"Ověření: 2·3 + ({b}) = {2*3 + b}")
```
### Ze dvou bodů
```{python}
def primka_ze_dvou_bodu(bod1, bod2):
"""Vrátí rovnici přímky procházející dvěma body."""
a = smernice(bod1, bod2)
b = bod1[1] - a * bod1[0]
return a, b
# Přímka procházející body [1, 2] a [3, 8]
A = [1, 2]
B = [3, 8]
a, b = primka_ze_dvou_bodu(A, B)
print(f"Rovnice přímky: y = {a}x + {b}")
```
## Průsečíky
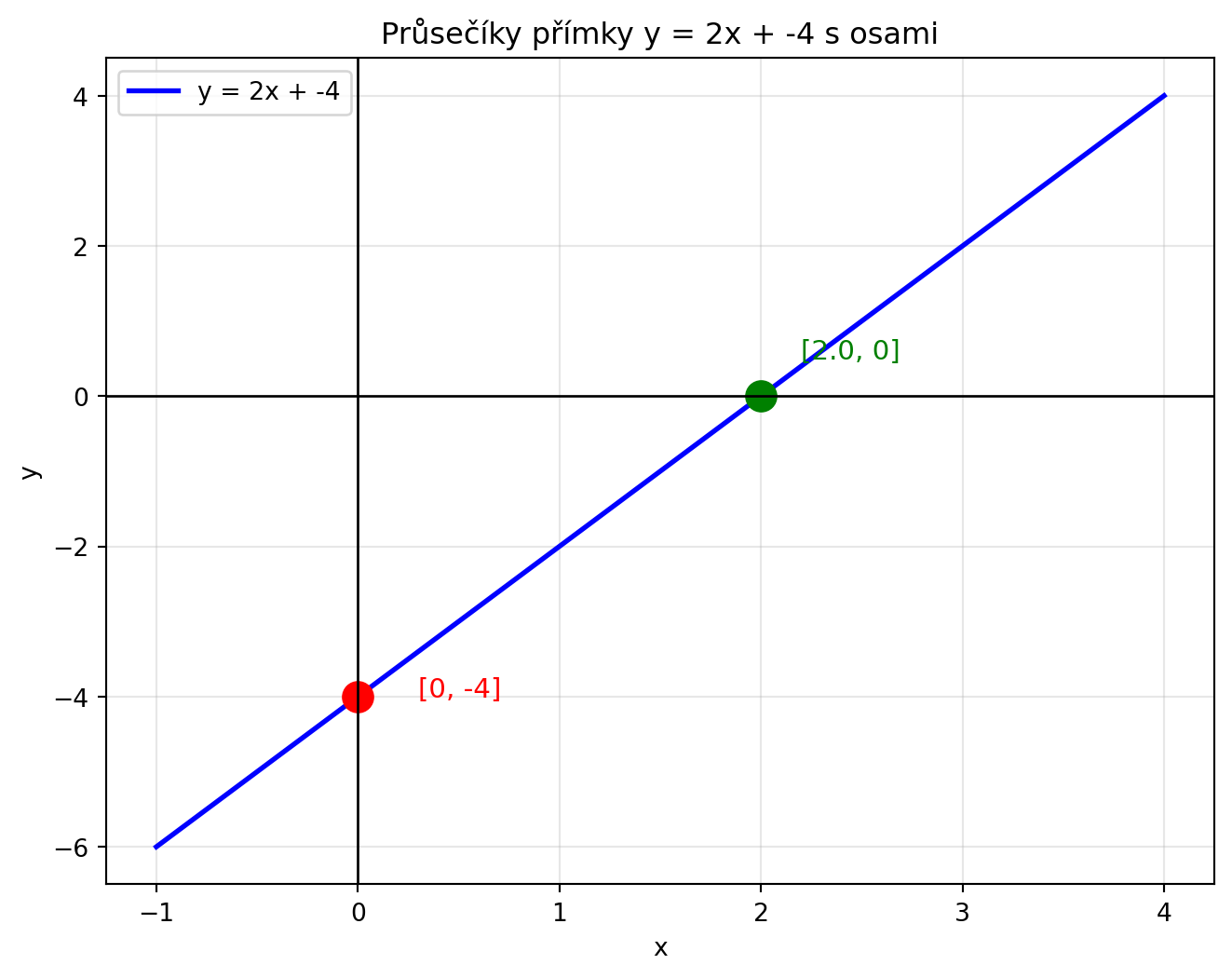
### Průsečík s osou x
Průsečík s osou x najdeme tak, že položíme $y = 0$:
$$0 = ax + b \Rightarrow x = -\frac{b}{a}$$
### Průsečík s osou y
Průsečík s osou y je přímo hodnota *b* (protože pro $x = 0$ dostaneme $y = b$).
```{python}
#| fig-cap: "Průsečíky s osami"
import numpy as np
import matplotlib.pyplot as plt
def prumky_s_osami(a, b):
"""Najde průsečíky přímky y = ax + b s osami."""
prusecik_y = b # Pro x = 0
prusecik_x = -b / a # Pro y = 0
return prusecik_x, prusecik_y
# Pro přímku y = 2x - 4
a, b = 2, -4
px, py = prumky_s_osami(a, b)
x = np.linspace(-1, 4, 100)
y = a * x + b
plt.figure(figsize=(8, 6))
plt.plot(x, y, 'b-', linewidth=2, label=f'y = {a}x + {b}')
# Průsečíky
plt.plot(px, 0, 'go', markersize=12)
plt.plot(0, py, 'ro', markersize=12)
plt.annotate(f'[{px}, 0]', xy=(px, 0), xytext=(px+0.2, 0.5), fontsize=11, color='green')
plt.annotate(f'[0, {py}]', xy=(0, py), xytext=(0.3, py), fontsize=11, color='red')
plt.axhline(y=0, color='k', linewidth=1)
plt.axvline(x=0, color='k', linewidth=1)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title(f'Průsečíky přímky y = {a}x + {b} s osami')
plt.legend()
plt.show()
print(f"Průsečík s osou x: [{px}, 0]")
print(f"Průsečík s osou y: [0, {py}]")
```
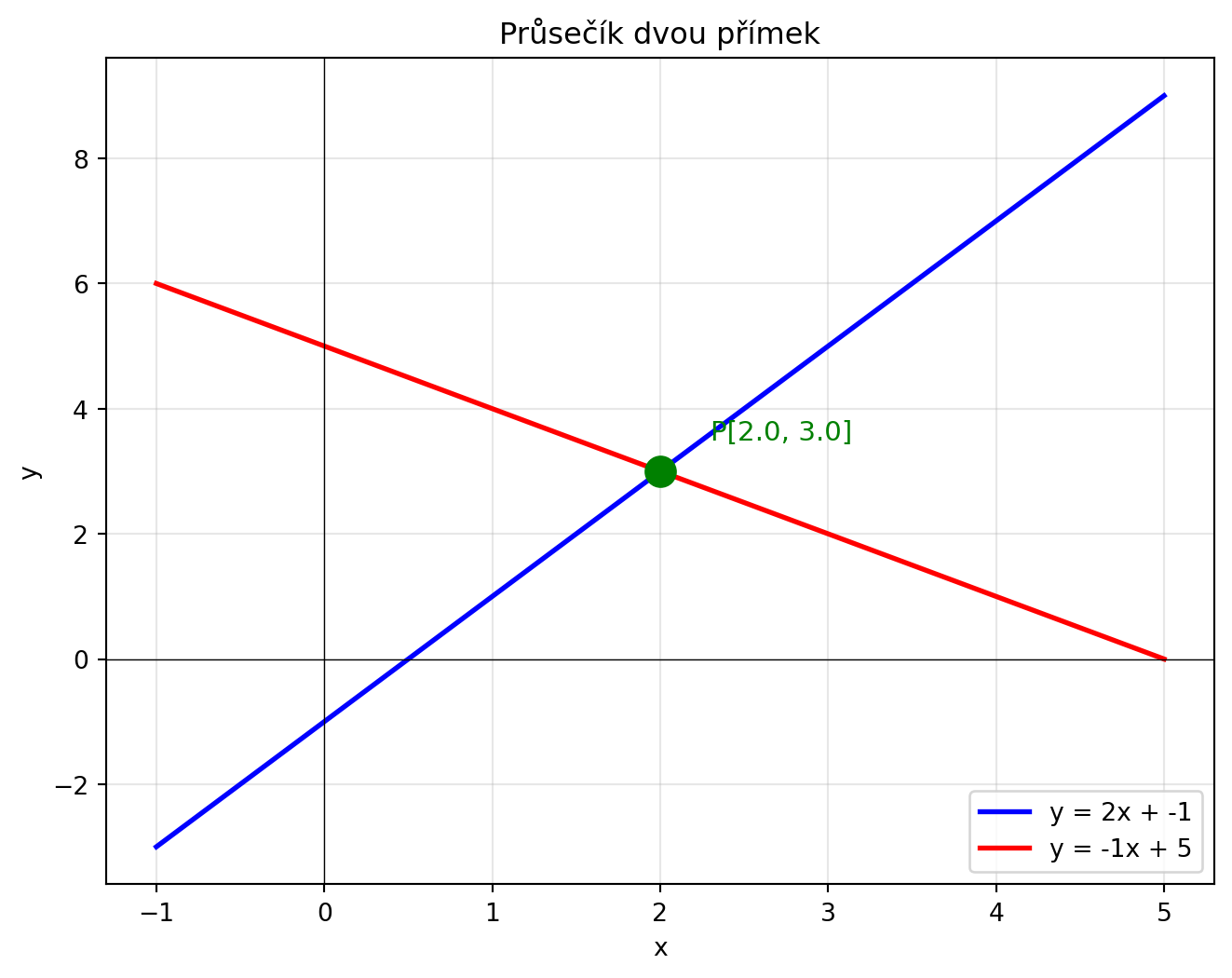
### Průsečík dvou přímek
Máme-li dvě přímky $y = a_1x + b_1$ a $y = a_2x + b_2$, jejich průsečík najdeme vyřešením soustavy rovnic:
$$a_1x + b_1 = a_2x + b_2$$
```{python}
#| fig-cap: "Průsečík dvou přímek"
import numpy as np
import matplotlib.pyplot as plt
def prusecik_primek(a1, b1, a2, b2):
"""Najde průsečík dvou přímek."""
if a1 == a2:
return None # Rovnoběžky nemají průsečík
x = (b2 - b1) / (a1 - a2)
y = a1 * x + b1
return x, y
# Přímky y = 2x - 1 a y = -x + 5
a1, b1 = 2, -1
a2, b2 = -1, 5
P = prusecik_primek(a1, b1, a2, b2)
x = np.linspace(-1, 5, 100)
plt.figure(figsize=(8, 6))
plt.plot(x, a1*x + b1, 'b-', linewidth=2, label=f'y = {a1}x + {b1}')
plt.plot(x, a2*x + b2, 'r-', linewidth=2, label=f'y = {a2}x + {b2}')
if P:
plt.plot(P[0], P[1], 'go', markersize=12)
plt.annotate(f'P[{P[0]:.1f}, {P[1]:.1f}]', xy=P, xytext=(P[0]+0.3, P[1]+0.5),
fontsize=11, color='green')
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Průsečík dvou přímek')
plt.legend()
plt.show()
print(f"Průsečík: P{P}")
```
---
## Lineární regrese -- predikce pomocí přímky
**Lineární regrese** je metoda, která najde přímku nejlépe procházející daty. Je to základní nástroj strojového učení!
### Příklad: Předpověď ceny
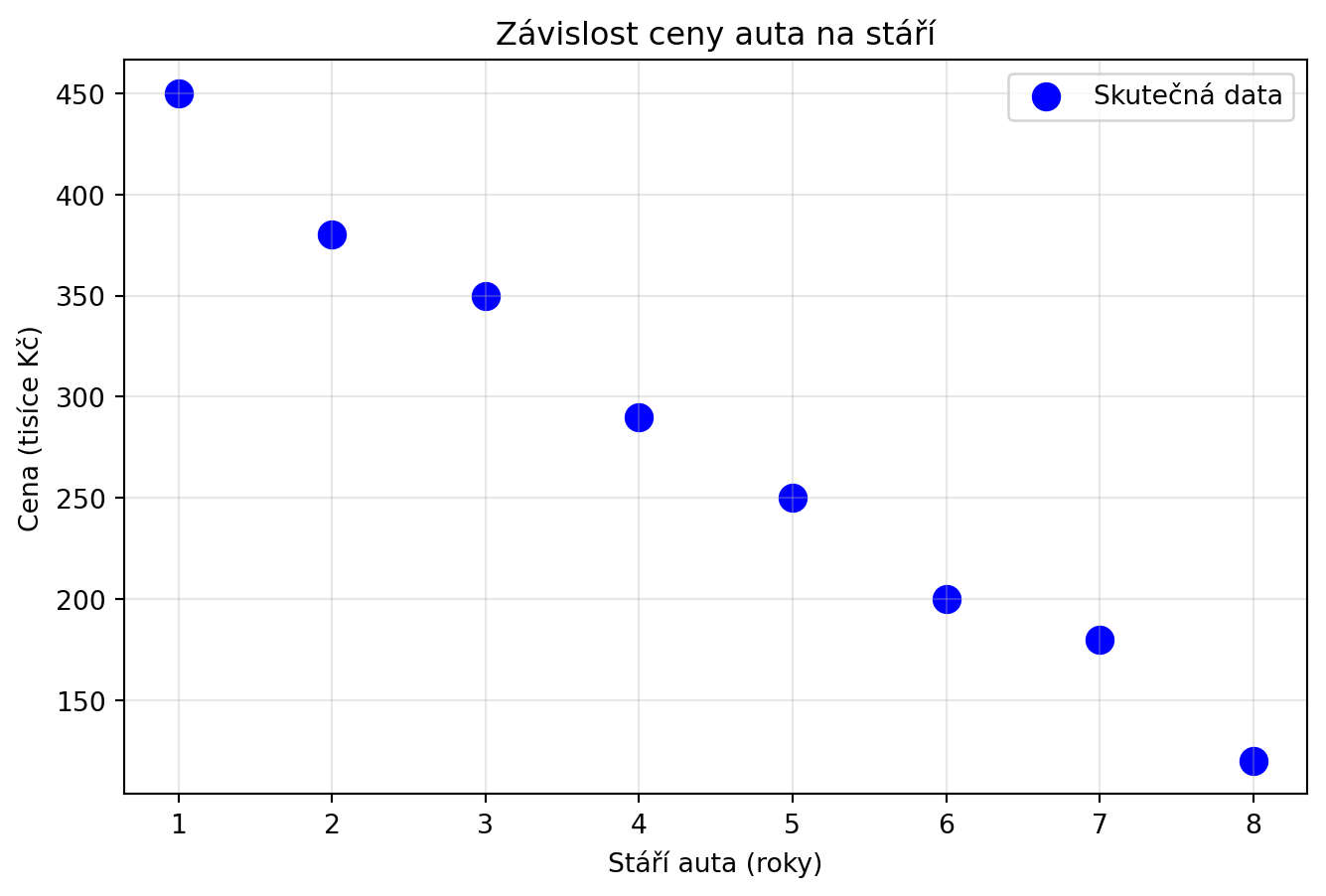
Máme data o stáří aut a jejich cenách:
```{python}
# Data: [stáří v letech, cena v tisících Kč]
import numpy as np
stari = np.array([1, 2, 3, 4, 5, 6, 7, 8])
cena = np.array([450, 380, 350, 290, 250, 200, 180, 120])
print("Stáří auta (roky):", stari)
print("Cena (tis. Kč): ", cena)
```
```{python}
#| fig-cap: "Data o cenách aut"
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 5))
plt.scatter(stari, cena, s=100, color='blue', label='Skutečná data')
plt.xlabel('Stáří auta (roky)')
plt.ylabel('Cena (tisíce Kč)')
plt.title('Závislost ceny auta na stáří')
plt.grid(True, alpha=0.3)
plt.legend()
plt.show()
```
### Použití NumPy pro lineární regresi
```{python}
#| fig-cap: "Lineární regrese"
# NumPy umí najít nejlepší přímku
import numpy as np
import matplotlib.pyplot as plt
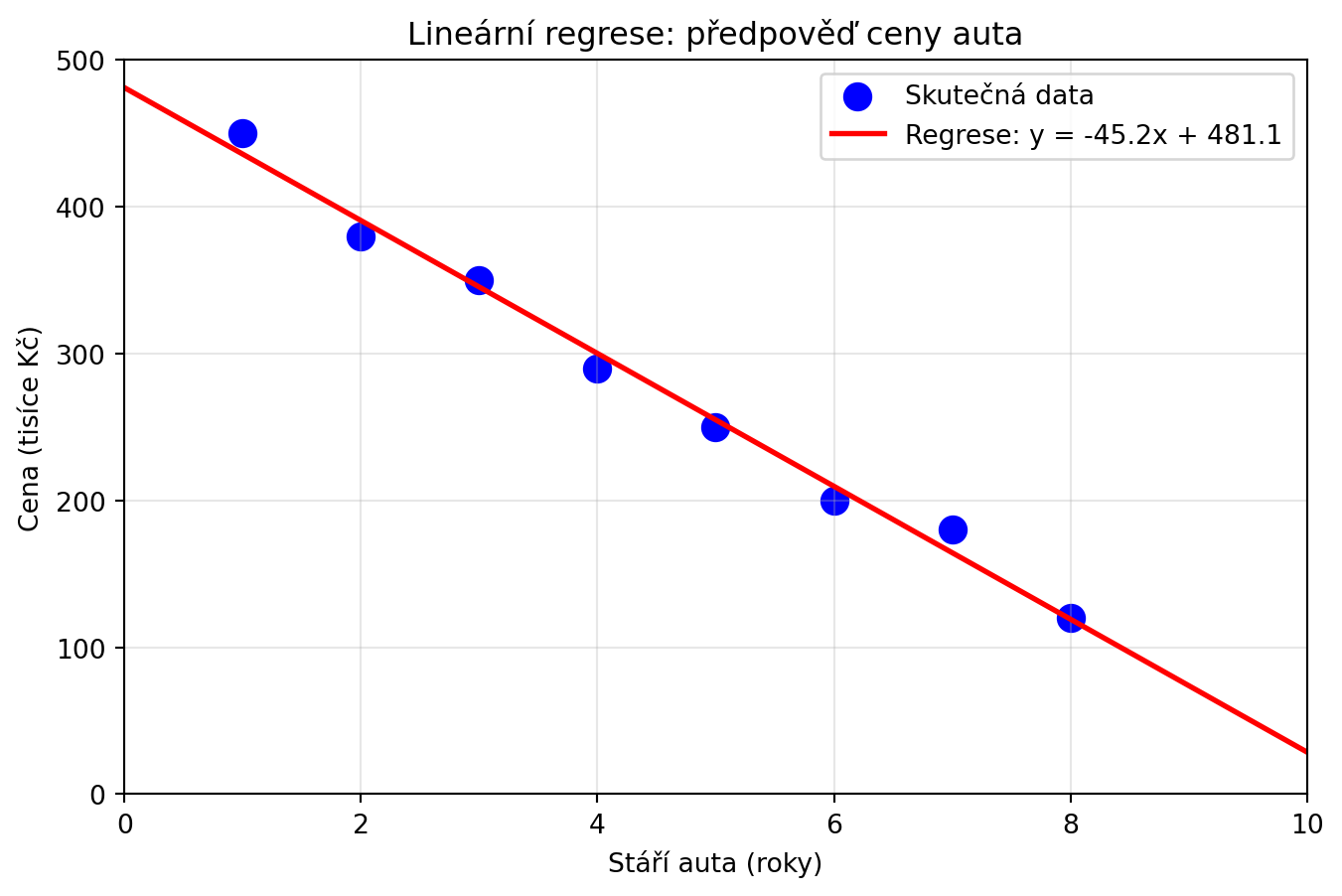
koeficienty = np.polyfit(stari, cena, 1) # 1 = lineární (stupeň 1)
a = koeficienty[0] # směrnice
b = koeficienty[1] # úsek
print(f"Rovnice přímky: cena = {a:.1f} × stáří + {b:.1f}")
# Vykreslení
plt.figure(figsize=(8, 5))
plt.scatter(stari, cena, s=100, color='blue', label='Skutečná data')
# Přímka regrese
x_regrese = np.linspace(0, 10, 100)
y_regrese = a * x_regrese + b
plt.plot(x_regrese, y_regrese, 'r-', linewidth=2, label=f'Regrese: y = {a:.1f}x + {b:.1f}')
plt.xlabel('Stáří auta (roky)')
plt.ylabel('Cena (tisíce Kč)')
plt.title('Lineární regrese: předpověď ceny auta')
plt.grid(True, alpha=0.3)
plt.legend()
plt.xlim(0, 10)
plt.ylim(0, 500)
plt.show()
```
### Predikce
Teď můžeme předpovědět cenu pro libovolné stáří:
```{python}
def predikuj_cenu(stari_auta):
return a * stari_auta + b
print(f"Předpokládaná cena 5 let starého auta: {predikuj_cenu(5):.0f} tis. Kč")
print(f"Předpokládaná cena 10 let starého auta: {predikuj_cenu(10):.0f} tis. Kč")
print(f"Předpokládaná cena nového auta: {predikuj_cenu(0):.0f} tis. Kč")
```
::: {.callout-tip title="Důležité pro strojové učení"}
Lineární regrese je jeden z nejjednodušších modelů strojového učení. Principy jsou stejné i u složitějších modelů:
1. Máme **data** (vstupy a výstupy)
2. Hledáme **model** (funkci), který data popisuje
3. Model používáme pro **predikce** na nových datech
:::
---
## Řešené příklady
### Příklad 1: Určení rovnice přímky
Určete rovnici přímky, která prochází bodem [2, 5] a má směrnici 3.
**Řešení:**
$y = ax + b$, kde $a = 3$
Dosadíme bod [2, 5]: $5 = 3 \cdot 2 + b$
$b = 5 - 6 = -1$
**Rovnice: $y = 3x - 1$**
```{python}
a, b = primka_ze_smernice_a_bodu(3, [2, 5])
print(f"Rovnice: y = {a}x + {b}")
```
### Příklad 2: Přímka dvěma body
Najděte rovnici přímky procházející body A[-1, 4] a B[2, -2].
```{python}
A = [-1, 4]
B = [2, -2]
a, b = primka_ze_dvou_bodu(A, B)
print(f"Směrnice: a = (−2 − 4)/(2 − (−1)) = −6/3 = {a}")
print(f"Rovnice: y = {a}x + {b}")
# Ověření
print(f"\nOvěření bod A: {a}·(-1) + {b} = {a*(-1) + b}")
print(f"Ověření bod B: {a}·2 + {b} = {a*2 + b}")
```
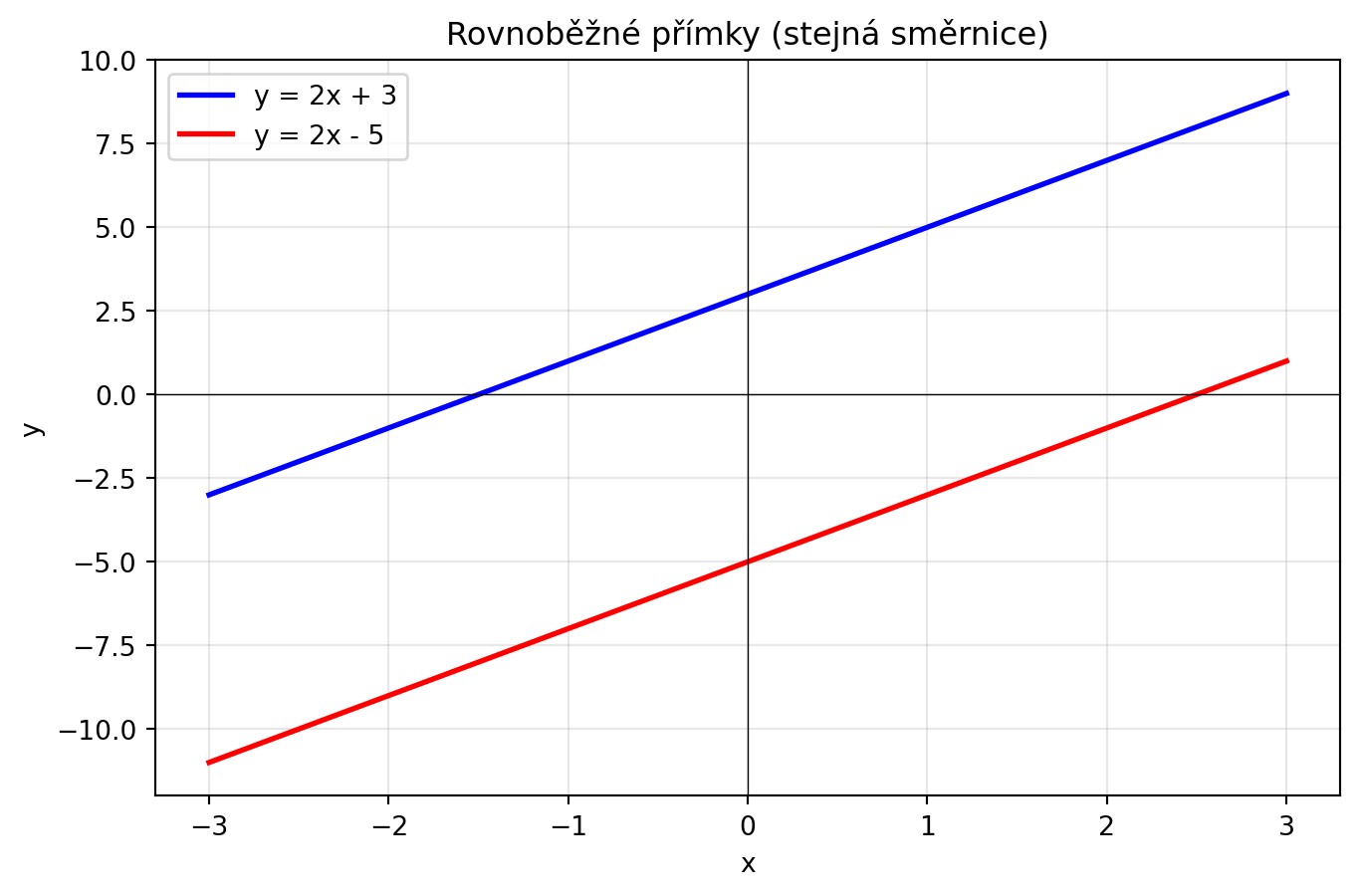
### Příklad 3: Jsou přímky rovnoběžné?
Jsou přímky $y = 2x + 3$ a $y = 2x - 5$ rovnoběžné?
**Řešení:** Ano, protože mají **stejnou směrnici** (a = 2).
```{python}
#| fig-cap: "Rovnoběžné přímky"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
plt.figure(figsize=(8, 5))
plt.plot(x, 2*x + 3, 'b-', linewidth=2, label='y = 2x + 3')
plt.plot(x, 2*x - 5, 'r-', linewidth=2, label='y = 2x - 5')
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Rovnoběžné přímky (stejná směrnice)')
plt.legend()
plt.show()
```
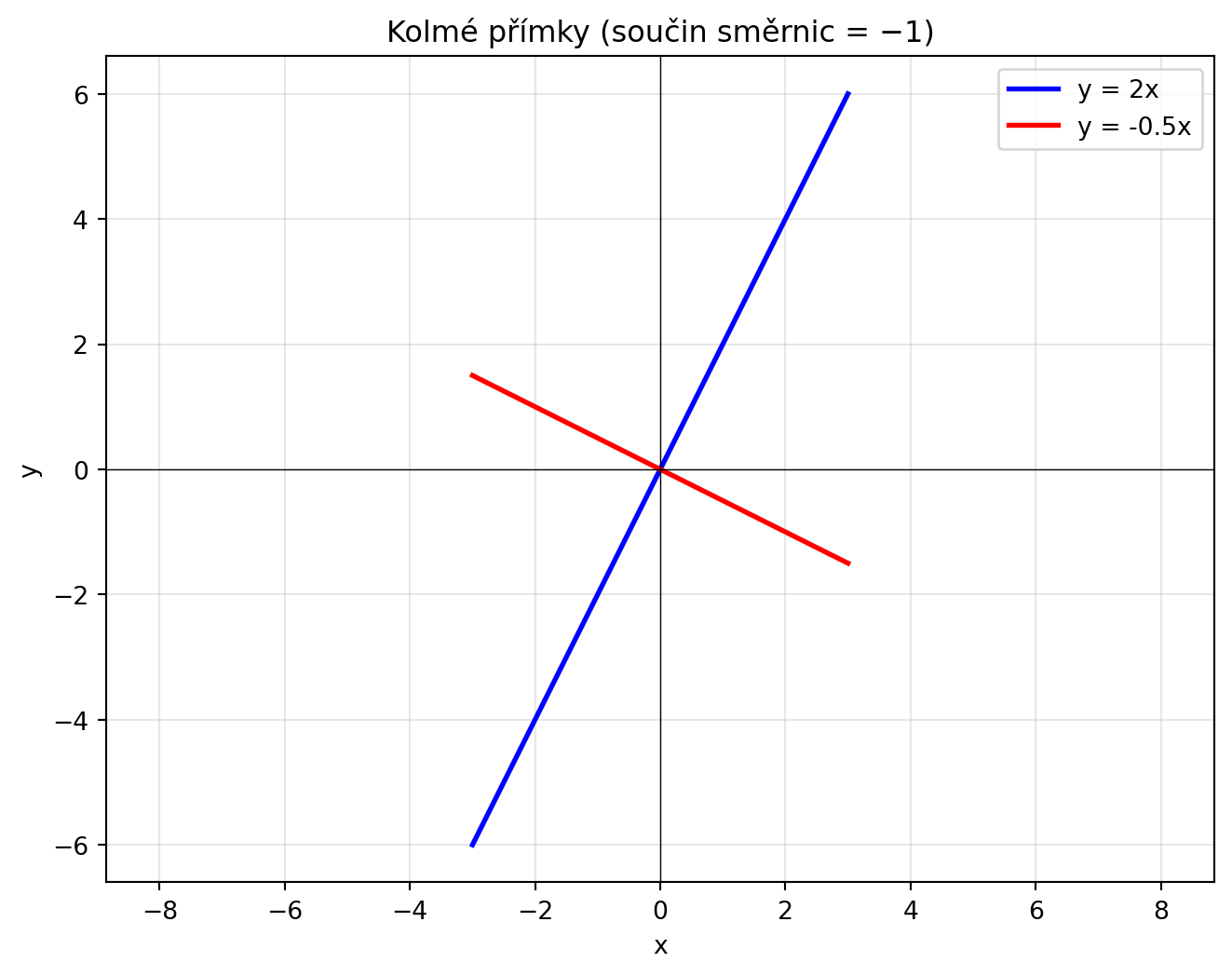
### Příklad 4: Kolmé přímky
Přímky jsou **kolmé**, když součin jejich směrnic je −1: $a_1 \cdot a_2 = -1$
```{python}
#| fig-cap: "Kolmé přímky"
# Přímka y = 2x a kolmá přímka y = -0.5x
import numpy as np
import matplotlib.pyplot as plt
a1 = 2
a2 = -1/a1 # Kolmá směrnice
print(f"Směrnice první přímky: {a1}")
print(f"Směrnice kolmé přímky: {a2}")
print(f"Součin směrnic: {a1 * a2}")
x = np.linspace(-3, 3, 100)
plt.figure(figsize=(8, 6))
plt.plot(x, a1*x, 'b-', linewidth=2, label=f'y = {a1}x')
plt.plot(x, a2*x, 'r-', linewidth=2, label=f'y = {a2}x')
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Kolmé přímky (součin směrnic = −1)')
plt.legend()
plt.axis('equal')
plt.show()
```
### Příklad 5: Praktická úloha
Taxi účtuje 40 Kč nástupné + 25 Kč za km. Kolik stojí jízda 8 km? Kolik km ujedete za 200 Kč?
```{python}
def cena_taxi(km):
return 40 + 25 * km
def km_za_cenu(cena):
return (cena - 40) / 25
print(f"Cena za 8 km: {cena_taxi(8)} Kč")
print(f"Km za 200 Kč: {km_za_cenu(200)} km")
```
---
## Cvičení
::: {.callout-warning title="Cvičení 1: Základní rovnice"}
Napište rovnici přímky se směrnicí 4 a úsekem na ose y rovným -3.
**Výsledek:** y = 4x - 3
:::
::: {.callout-warning title="Cvičení 2: Z bodů"}
Najděte rovnici přímky procházející body [0, 2] a [3, 8].
**Výsledek:** y = 2x + 2
<details>
<summary>Řešení</summary>
$a = \frac{8-2}{3-0} = \frac{6}{3} = 2$
Pro x = 0: y = 2, tedy b = 2
Rovnice: y = 2x + 2
</details>
:::
::: {.callout-warning title="Cvičení 3: Průsečíky"}
Najděte průsečíky přímky y = 3x - 6 s oběma osami.
**Výsledek:** [2, 0] a [0, -6]
:::
::: {.callout-warning title="Cvičení 4: Průsečík přímek"}
Najděte průsečík přímek y = x + 1 a y = -2x + 7.
**Výsledek:** [2, 3]
:::
::: {.callout-warning title="Cvičení 5: Lineární regrese"}
Data:
- x = [1, 2, 3, 4, 5]
- y = [2.1, 3.9, 6.2, 7.8, 10.1]
Použijte `np.polyfit()` k nalezení nejlepší přímky.
<details>
<summary>Řešení</summary>
```python
import numpy as np
x = np.array([1, 2, 3, 4, 5])
y = np.array([2.1, 3.9, 6.2, 7.8, 10.1])
koef = np.polyfit(x, y, 1)
print(f"y = {koef[0]:.2f}x + {koef[1]:.2f}")
# Výsledek: přibližně y = 2x + 0
```
</details>
:::
::: {.callout-warning title="Cvičení 6: Kolmá přímka"}
Najděte rovnici přímky, která je kolmá na přímku y = 3x + 1 a prochází bodem [6, 2].
<details>
<summary>Nápověda</summary>
Kolmá směrnice je -1/3
</details>
<details>
<summary>Řešení</summary>
$a = -\frac{1}{3}$
$2 = -\frac{1}{3} \cdot 6 + b$
$b = 2 + 2 = 4$
Rovnice: $y = -\frac{1}{3}x + 4$
</details>
:::
---
## Shrnutí
::: {.callout-note title="Co si zapamatovat"}
- Lineární funkce: $y = ax + b$
- **Směrnice** *a* určuje sklon (kladná = roste, záporná = klesá)
- **Úsek** *b* je hodnota y pro x = 0
- Směrnice ze dvou bodů: $a = \frac{y_2 - y_1}{x_2 - x_1}$
- Rovnoběžné přímky mají **stejnou směrnici**
- Kolmé přímky: $a_1 \cdot a_2 = -1$
- **Lineární regrese** hledá nejlepší přímku pro data
- V Pythonu: `np.polyfit(x, y, 1)` pro lineární regresi
:::
V další kapitole se podíváme na **nelineární funkce** -- paraboly, exponenciály a logaritmy, které jsou klíčové pro pochopení neuronových sítí.