# Náhoda a pravděpodobnost {#sec-pravdepodobnost}
## Motivace: Jak předpovědět nepředvídatelné?
Představte si, že píšete zprávu a napíšete "Dnes je krásný...". Jaké slovo nejspíš následuje? Asi "den" - ale proč? Protože na základě zkušenosti víme, že slovo "den" po "krásný" následuje často.
Jazykové modely dělají přesně tohle - **předpovídají pravděpodobnost dalšího slova**. Když ChatGPT generuje text, v každém kroku počítá pravděpodobnosti všech možných slov a vybírá podle nich.
Pravděpodobnost je jazyk, kterým popisujeme **nejistotu** a **náhodnost**. V této kapitole se naučíme základy:
- Co je pravděpodobnost a jak ji měříme
- Základní pravidla pro počítání s pravděpodobnostmi
- Podmíněnou pravděpodobnost - jak nové informace mění naše odhady
- Bayesovu větu - nástroj pro aktualizaci přesvědčení
## Co je pravděpodobnost?
Pravděpodobnost je číslo mezi 0 a 1, které vyjadřuje, jak moc je nějaká událost "pravděpodobná":
- **0** = událost nenastane nikdy
- **1** = událost nastane jistě
- **0.5** = událost nastane v polovině případů
::: {.callout-note}
## Definice: Pravděpodobnost
Pravděpodobnost události $A$ značíme $P(A)$ a platí:
$$0 \leq P(A) \leq 1$$
- $P(A) = 0$ znamená, že $A$ je nemožná
- $P(A) = 1$ znamená, že $A$ je jistá
:::
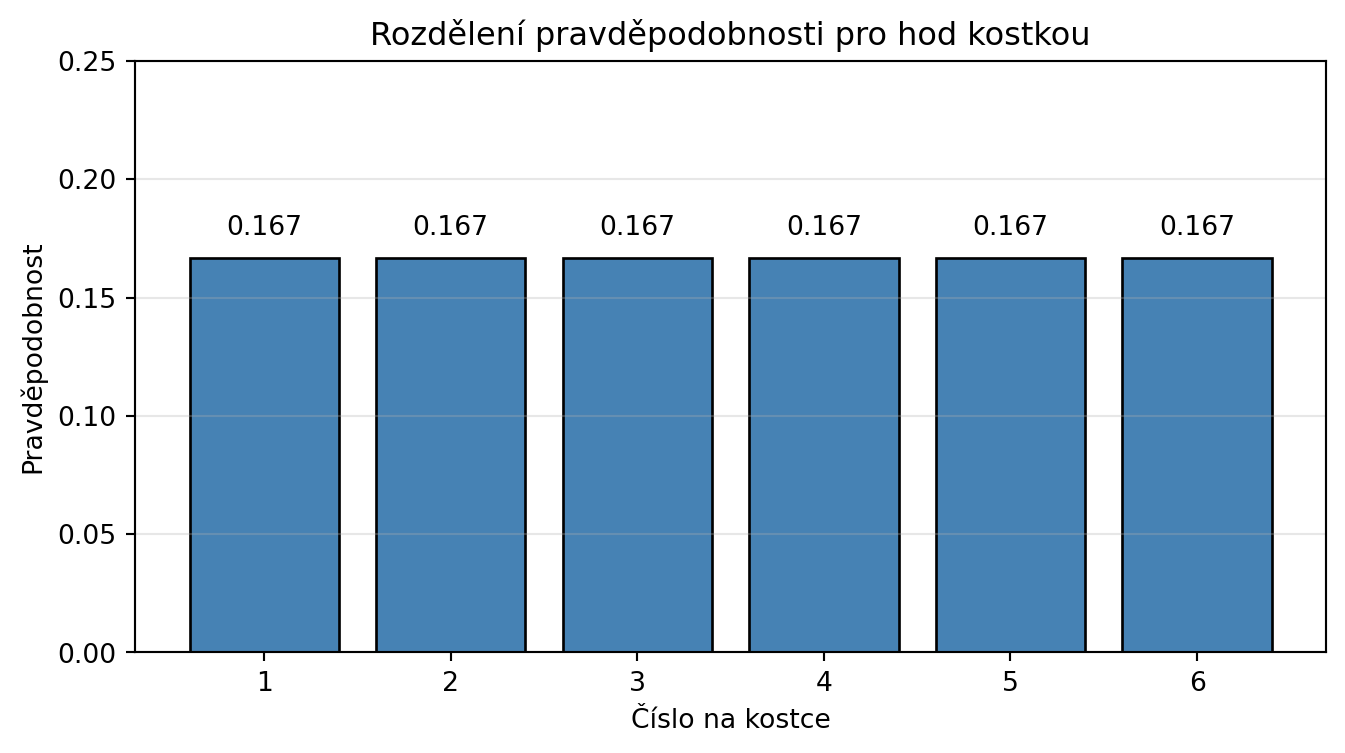
### Příklad: Hod kostkou
Při hodu spravedlivou kostkou má každé číslo stejnou pravděpodobnost:
```{python}
import numpy as np
import matplotlib.pyplot as plt
# Pravděpodobnosti pro kostku
cisla = [1, 2, 3, 4, 5, 6]
pravdepodobnosti = [1/6] * 6
plt.figure(figsize=(8, 4))
plt.bar(cisla, pravdepodobnosti, color='steelblue', edgecolor='black')
plt.xlabel('Číslo na kostce')
plt.ylabel('Pravděpodobnost')
plt.title('Rozdělení pravděpodobnosti pro hod kostkou')
plt.ylim(0, 0.25)
for i, p in enumerate(pravdepodobnosti):
plt.text(i+1, p + 0.01, f'{p:.3f}', ha='center')
plt.grid(axis='y', alpha=0.3)
plt.show()
print(f"P(padne 3) = {1/6:.4f}")
print(f"P(padne sudé číslo) = P(2) + P(4) + P(6) = {3/6:.4f}")
print(f"Součet všech pravděpodobností = {sum(pravdepodobnosti):.4f}")
```
### Simulace náhodných jevů
Python nám umožňuje simulovat náhodné jevy a ověřovat pravděpodobnosti experimentálně:
```{python}
import numpy as np
np.random.seed(42)
# Simulace 10000 hodů kostkou
hody = np.random.randint(1, 7, size=10000)
# Spočítáme četnosti
unique, counts = np.unique(hody, return_counts=True)
relativni_cetnosti = counts / len(hody)
print("Relativní četnosti po 10000 hodech:")
for cislo, cetnost in zip(unique, relativni_cetnosti):
print(f" Číslo {cislo}: {cetnost:.4f} (teoreticky {1/6:.4f})")
```
::: {.callout-tip}
## Zákon velkých čísel
Čím více pokusů provedeme, tím blíže se relativní četnost blíží teoretické pravděpodobnosti. Tomu říkáme **zákon velkých čísel**.
:::
## Základní pravidla pravděpodobnosti
### Pravidlo součtu (OR)
Pravděpodobnost, že nastane $A$ **nebo** $B$ (alespoň jedna z událostí):
$$P(A \cup B) = P(A) + P(B) - P(A \cap B)$$
Pokud se $A$ a $B$ vzájemně vylučují (nemohou nastat současně):
$$P(A \cup B) = P(A) + P(B)$$
```{python}
# Příklad: Hod kostkou
# A = padne číslo menší než 3 (1 nebo 2)
# B = padne sudé číslo (2, 4, 6)
P_A = 2/6 # {1, 2}
P_B = 3/6 # {2, 4, 6}
P_A_a_B = 1/6 # {2} - společný prvek
P_A_nebo_B = P_A + P_B - P_A_a_B
print(f"P(A) = P(číslo < 3) = {P_A:.4f}")
print(f"P(B) = P(sudé) = {P_B:.4f}")
print(f"P(A ∩ B) = P(2) = {P_A_a_B:.4f}")
print(f"P(A ∪ B) = P(A) + P(B) - P(A ∩ B) = {P_A_nebo_B:.4f}")
print(f"\nOvěření: {1, 2, 4, 6} má 4 prvky, P = 4/6 = {4/6:.4f}")
```
### Pravidlo součinu (AND)
Pravděpodobnost, že nastane $A$ **a zároveň** $B$:
$$P(A \cap B) = P(A) \cdot P(B|A)$$
kde $P(B|A)$ je pravděpodobnost $B$ za předpokladu, že nastalo $A$.
Pokud jsou $A$ a $B$ **nezávislé** (jedno neovlivňuje druhé):
$$P(A \cap B) = P(A) \cdot P(B)$$
```{python}
# Příklad: Dva hody kostkou
# A = první hod je 6
# B = druhý hod je 6
P_A = 1/6
P_B = 1/6
# Hody jsou nezávislé
P_A_a_B = P_A * P_B
print(f"P(první = 6) = {P_A:.4f}")
print(f"P(druhý = 6) = {P_B:.4f}")
print(f"P(oba = 6) = {P_A * P_B:.4f}")
print(f"\nŠance hodit dvě šestky: 1 z {int(1/P_A_a_B)}")
```
### Doplněk
Pravděpodobnost, že událost $A$ **nenastane**:
$$P(\neg A) = 1 - P(A)$$
```{python}
# Pravděpodobnost, že při hodu kostkou nepadne 6
P_sest = 1/6
P_ne_sest = 1 - P_sest
print(f"P(padne 6) = {P_sest:.4f}")
print(f"P(nepadne 6) = {P_ne_sest:.4f}")
```
## Podmíněná pravděpodobnost
Podmíněná pravděpodobnost $P(A|B)$ je pravděpodobnost události $A$, **pokud víme, že nastala událost $B$**.
::: {.callout-note}
## Definice: Podmíněná pravděpodobnost
$$P(A|B) = \frac{P(A \cap B)}{P(B)}$$
Čteme: "pravděpodobnost A za předpokladu B"
:::
### Příklad: Karty
```{python}
# Máme balíček 52 karet
# A = karta je eso
# B = karta je srdcová
P_eso = 4/52 # 4 esa v balíčku
P_srdce = 13/52 # 13 srdcových karet
P_eso_a_srdce = 1/52 # jen srdcové eso
# P(eso | srdce) = pravděpodobnost esa, když víme, že karta je srdcová
P_eso_kdyz_srdce = P_eso_a_srdce / P_srdce
print(f"P(eso) = {P_eso:.4f}")
print(f"P(srdce) = {P_srdce:.4f}")
print(f"P(eso ∩ srdce) = {P_eso_a_srdce:.4f}")
print(f"\nP(eso | srdce) = {P_eso_kdyz_srdce:.4f}")
print(f" = 1/13 (jedno eso mezi 13 srdcovými kartami)")
```
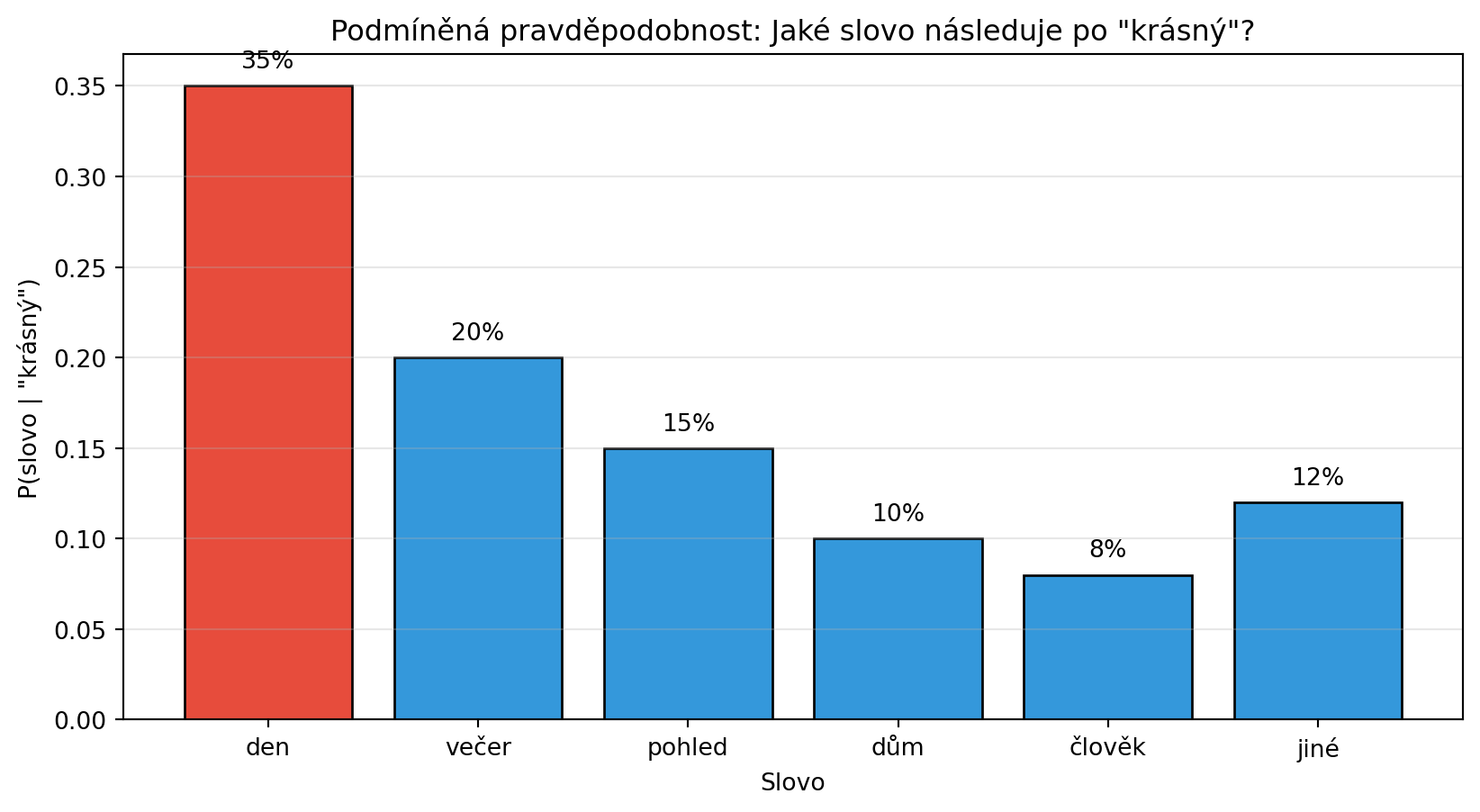
### Příklad: Jazykový model
V jazykovém modelu nás zajímá podmíněná pravděpodobnost dalšího slova:
```{python}
# Zjednodušený příklad: pravděpodobnosti slov po "krásný"
import matplotlib.pyplot as plt
slova_po_krasny = {
"den": 0.35,
"večer": 0.20,
"pohled": 0.15,
"dům": 0.10,
"člověk": 0.08,
"jiné": 0.12
}
plt.figure(figsize=(10, 5))
slova = list(slova_po_krasny.keys())
probs = list(slova_po_krasny.values())
colors = ['#e74c3c' if s == 'den' else '#3498db' for s in slova]
bars = plt.bar(slova, probs, color=colors, edgecolor='black')
plt.xlabel('Slovo')
plt.ylabel('P(slovo | "krásný")')
plt.title('Podmíněná pravděpodobnost: Jaké slovo následuje po "krásný"?')
for bar, p in zip(bars, probs):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.01,
f'{p:.0%}', ha='center')
plt.grid(axis='y', alpha=0.3)
plt.show()
print("Jazykový model by nejpravděpodobněji vybral slovo 'den'")
```
## Bayesova věta
Bayesova věta je mocný nástroj, který nám umožňuje **aktualizovat naše přesvědčení** na základě nových důkazů.
::: {.callout-note}
## Bayesova věta
$$P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}$$
Kde:
- $P(A)$ = **apriorní pravděpodobnost** (před důkazem)
- $P(A|B)$ = **posteriorní pravděpodobnost** (po důkazu)
- $P(B|A)$ = **věrohodnost** (jak pravděpodobný je důkaz, pokud platí A)
- $P(B)$ = **marginální pravděpodobnost** důkazu
:::
### Příklad: Lékařský test
Představte si test na vzácnou nemoc:
- Nemoc má 1 % populace
- Test je 95% spolehlivý (správně odhalí nemocného)
- Test má 5% falešně pozitivních (zdravý člověk je označen jako nemocný)
**Otázka**: Pokud vám test vyšel pozitivní, jaká je pravděpodobnost, že jste skutečně nemocní?
```{python}
# Apriorní pravděpodobnosti
P_nemoc = 0.01 # 1% má nemoc
P_zdravy = 0.99
# Podmíněné pravděpodobnosti (vlastnosti testu)
P_pozitivni_kdyz_nemoc = 0.95 # senzitivita
P_pozitivni_kdyz_zdravy = 0.05 # falešně pozitivní
# Celková pravděpodobnost pozitivního testu
P_pozitivni = (P_pozitivni_kdyz_nemoc * P_nemoc +
P_pozitivni_kdyz_zdravy * P_zdravy)
# Bayesova věta: P(nemoc | pozitivní)
P_nemoc_kdyz_pozitivni = (P_pozitivni_kdyz_nemoc * P_nemoc) / P_pozitivni
print("Lékařský test - Bayesova věta")
print("=" * 40)
print(f"P(nemoc) = {P_nemoc:.2%}")
print(f"P(pozitivní | nemoc) = {P_pozitivni_kdyz_nemoc:.2%}")
print(f"P(pozitivní | zdravý) = {P_pozitivni_kdyz_zdravy:.2%}")
print(f"\nP(pozitivní) = {P_pozitivni:.4f}")
print(f"\nP(nemoc | pozitivní) = {P_nemoc_kdyz_pozitivni:.2%}")
print(f"\nI přes pozitivní test je šance nemoci jen ~{P_nemoc_kdyz_pozitivni:.0%}!")
```
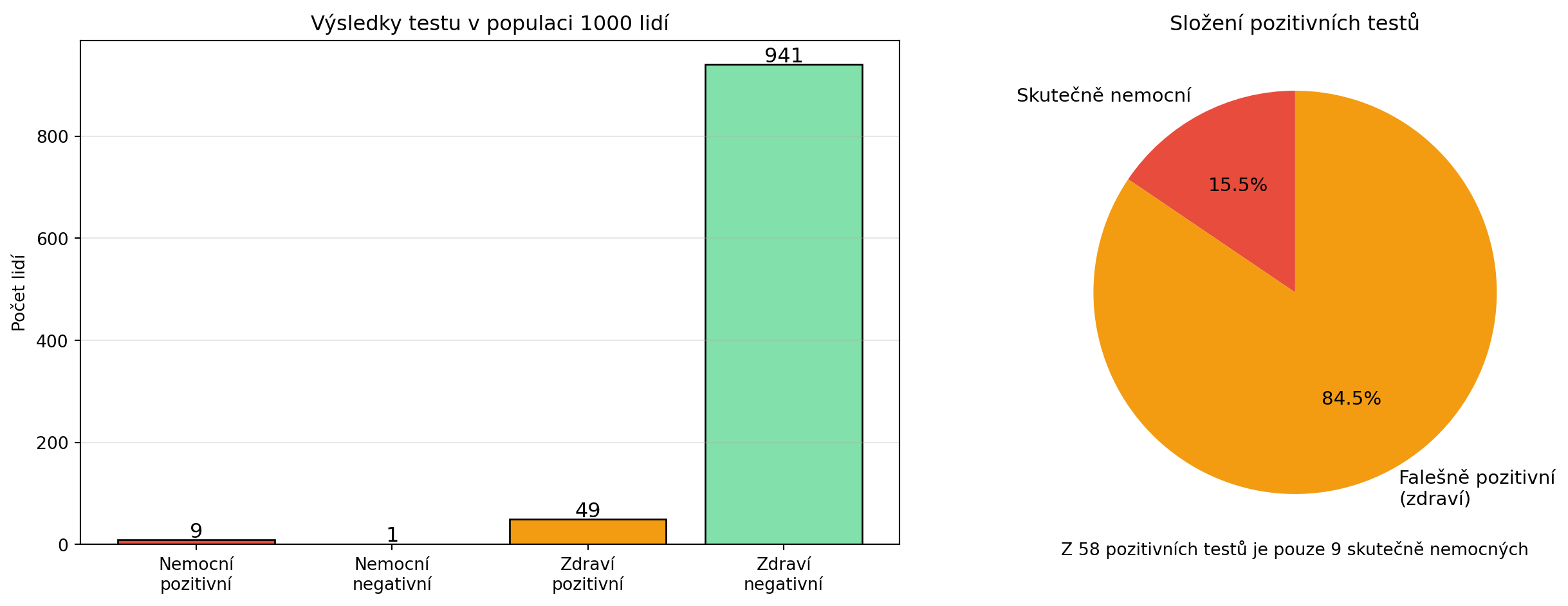
Tento překvapivý výsledek ukazuje, proč je Bayesova věta tak důležitá. Intuitivně bychom čekali vyšší pravděpodobnost nemoci, ale protože je nemoc vzácná, většina pozitivních testů jsou falešně pozitivní.
### Vizualizace Bayesova věta
```{python}
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 2, figsize=(14, 5))
# Levý graf: Populace 1000 lidí
ax1 = axes[0]
populace = 1000
nemocnych = int(populace * P_nemoc)
zdravych = populace - nemocnych
# Test výsledky
nemocni_pozitivni = int(nemocnych * P_pozitivni_kdyz_nemoc)
nemocni_negativni = nemocnych - nemocni_pozitivni
zdravi_pozitivni = int(zdravych * P_pozitivni_kdyz_zdravy)
zdravi_negativni = zdravych - zdravi_pozitivni
categories = ['Nemocní\npozitivní', 'Nemocní\nnegativní',
'Zdraví\npozitivní', 'Zdraví\nnegativní']
values = [nemocni_pozitivni, nemocni_negativni, zdravi_pozitivni, zdravi_negativni]
colors = ['#e74c3c', '#f1948a', '#f39c12', '#82e0aa']
bars = ax1.bar(categories, values, color=colors, edgecolor='black')
for bar, val in zip(bars, values):
ax1.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 5,
str(val), ha='center', fontsize=12)
ax1.set_ylabel('Počet lidí')
ax1.set_title(f'Výsledky testu v populaci {populace} lidí')
ax1.grid(axis='y', alpha=0.3)
# Pravý graf: Pouze pozitivní testy
ax2 = axes[1]
pozitivni_labels = ['Skutečně nemocní', 'Falešně pozitivní\n(zdraví)']
pozitivni_values = [nemocni_pozitivni, zdravi_pozitivni]
pozitivni_colors = ['#e74c3c', '#f39c12']
wedges, texts, autotexts = ax2.pie(pozitivni_values, labels=pozitivni_labels,
colors=pozitivni_colors, autopct='%1.1f%%',
startangle=90, textprops={'fontsize': 11})
ax2.set_title('Složení pozitivních testů')
celkem_pozitivnich = sum(pozitivni_values)
ax2.text(0, -1.3, f'Z {celkem_pozitivnich} pozitivních testů je pouze {nemocni_pozitivni} skutečně nemocných',
ha='center', fontsize=10)
plt.tight_layout()
plt.show()
```
## Nezávislost
Dvě události jsou **nezávislé**, pokud výskyt jedné neovlivňuje pravděpodobnost druhé:
$$P(A \cap B) = P(A) \cdot P(B)$$
nebo ekvivalentně:
$$P(A|B) = P(A)$$
```{python}
# Test nezávislosti: Dva hody mincí
import numpy as np
np.random.seed(42)
# Simulace 10000 dvojic hodů
hody1 = np.random.choice(['panna', 'orel'], size=10000)
hody2 = np.random.choice(['panna', 'orel'], size=10000)
# Podmíněné pravděpodobnosti
P_orel2 = np.mean(hody2 == 'orel')
P_orel2_kdyz_orel1 = np.mean(hody2[hody1 == 'orel'] == 'orel')
print("Test nezávislosti hodů mincí:")
print(f"P(2. hod = orel) = {P_orel2:.4f}")
print(f"P(2. hod = orel | 1. hod = orel) = {P_orel2_kdyz_orel1:.4f}")
print(f"\nHodnoty jsou podobné → hody jsou nezávislé")
```
::: {.callout-warning}
## Pozor na záměnu
**Nezávislost** (A neovlivňuje B) není totéž co **vzájemné vyloučení** (A a B nemohou nastat současně).
Vzájemně se vylučující události jsou naopak **závislé** - pokud nastala jedna, druhá nemůže nastat.
:::
## Řešené příklady
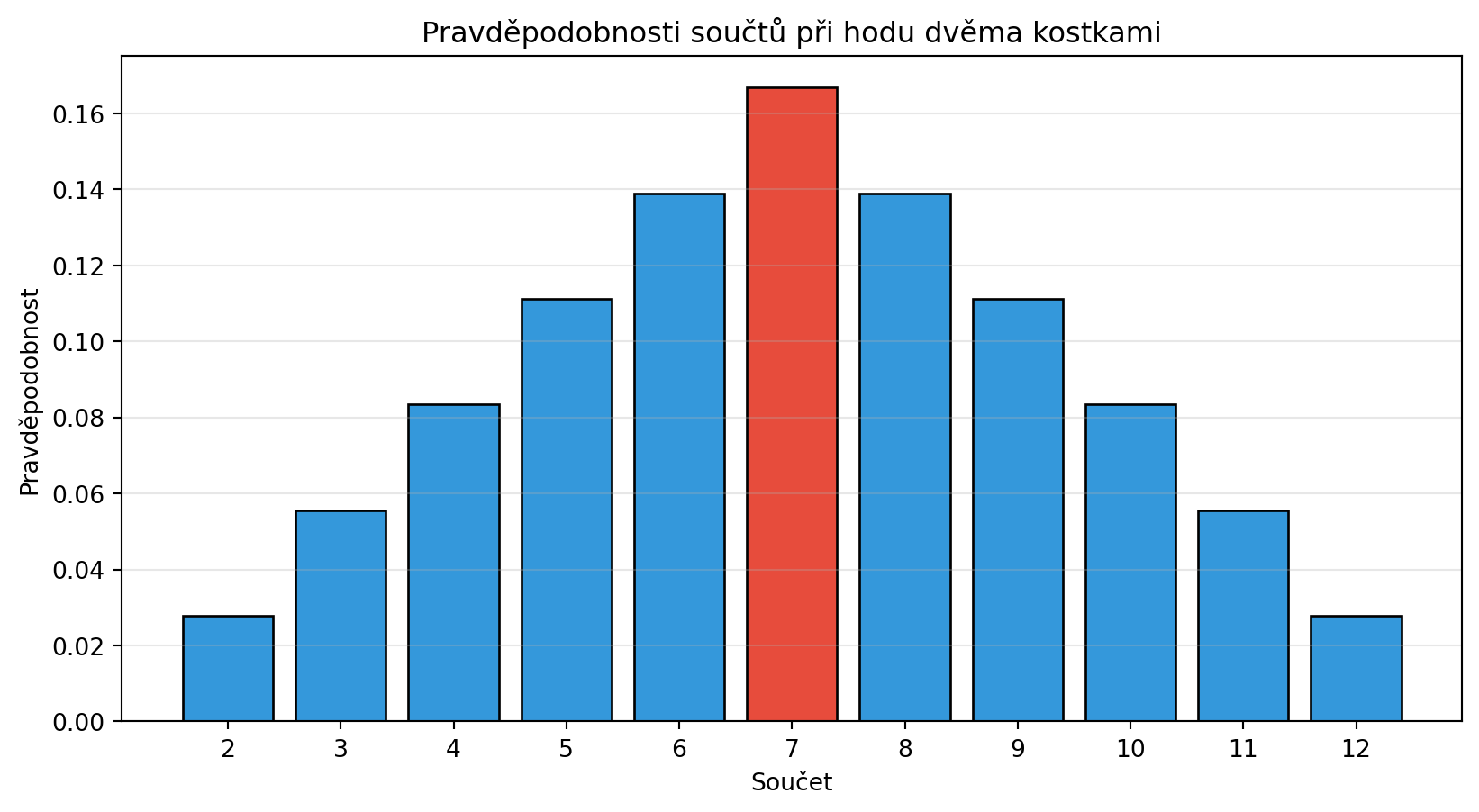
### Příklad 1: Hod dvěma kostkami
**Zadání**: Jaká je pravděpodobnost, že součet dvou kostek je 7?
**Řešení**:
```{python}
# Všechny možné kombinace
import matplotlib.pyplot as plt
kombinace_7 = [(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)]
celkem_kombinaci = 6 * 6
P_soucet_7 = len(kombinace_7) / celkem_kombinaci
print(f"Kombinace se součtem 7: {kombinace_7}")
print(f"Počet příznivých: {len(kombinace_7)}")
print(f"Počet všech: {celkem_kombinaci}")
print(f"P(součet = 7) = {len(kombinace_7)}/{celkem_kombinaci} = {P_soucet_7:.4f}")
# Vizualizace všech součtů
soucty = {}
for k1 in range(1, 7):
for k2 in range(1, 7):
s = k1 + k2
soucty[s] = soucty.get(s, 0) + 1
plt.figure(figsize=(10, 5))
x = list(soucty.keys())
y = [v/36 for v in soucty.values()]
colors = ['#e74c3c' if xi == 7 else '#3498db' for xi in x]
plt.bar(x, y, color=colors, edgecolor='black')
plt.xlabel('Součet')
plt.ylabel('Pravděpodobnost')
plt.title('Pravděpodobnosti součtů při hodu dvěma kostkami')
plt.xticks(range(2, 13))
plt.grid(axis='y', alpha=0.3)
plt.show()
```
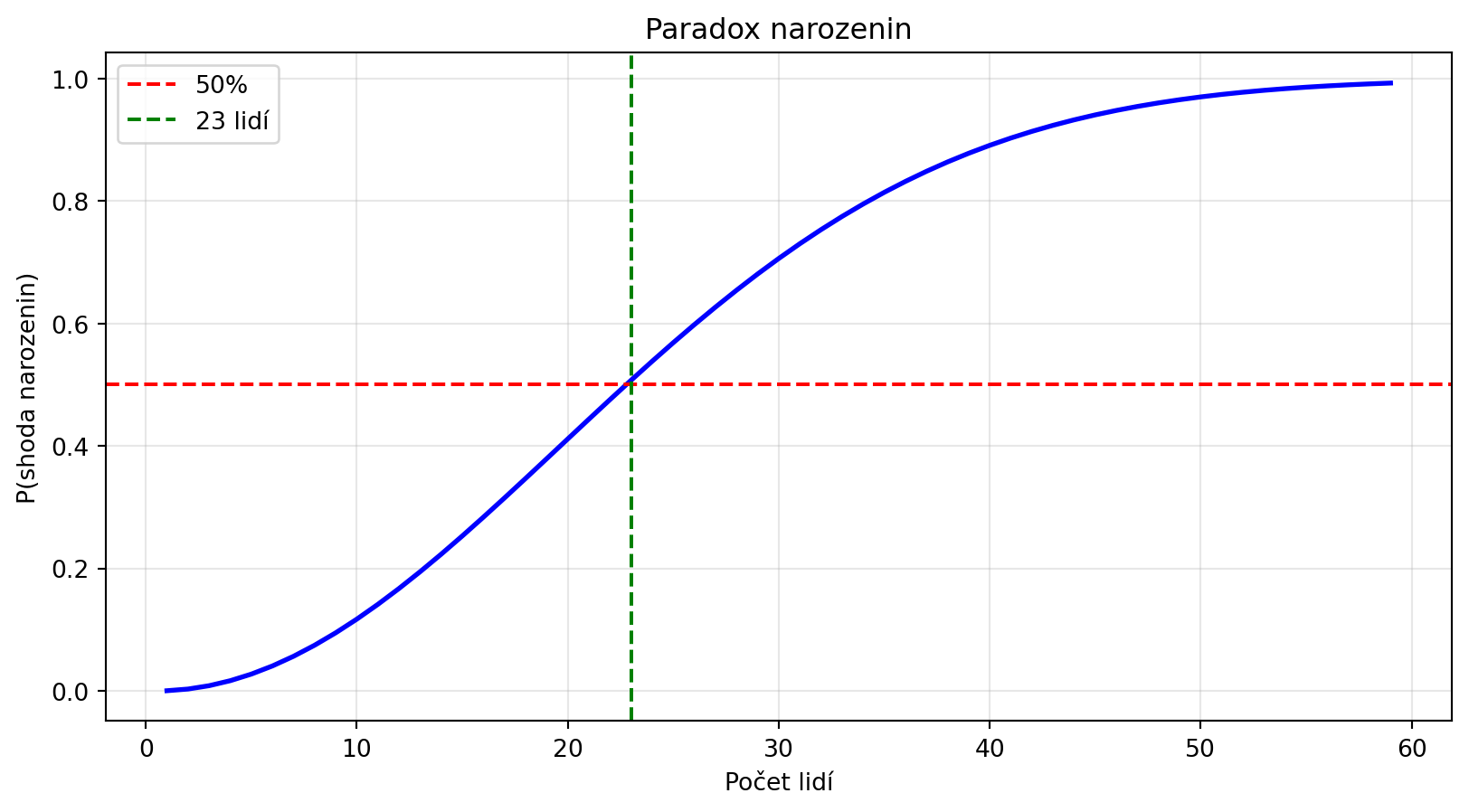
### Příklad 2: Narozeniny
**Zadání**: V místnosti je 23 lidí. Jaká je pravděpodobnost, že alespoň dva mají narozeniny ve stejný den?
**Řešení**:
```{python}
import matplotlib.pyplot as plt
def P_zadne_shody(n):
"""Pravděpodobnost, že žádní dva z n lidí nemají stejné narozeniny."""
p = 1.0
for i in range(n):
p *= (365 - i) / 365
return p
def P_shoda(n):
"""Pravděpodobnost alespoň jedné shody."""
return 1 - P_zadne_shody(n)
# Pro 23 lidí
n = 23
print(f"P(alespoň 2 lidé mají stejné narozeniny) = {P_shoda(n):.4f}")
print(f"Tedy více než 50%!")
# Graf pro různé počty lidí
lidi = range(1, 60)
pravdepodobnosti = [P_shoda(n) for n in lidi]
plt.figure(figsize=(10, 5))
plt.plot(lidi, pravdepodobnosti, 'b-', lw=2)
plt.axhline(y=0.5, color='r', linestyle='--', label='50%')
plt.axvline(x=23, color='g', linestyle='--', label='23 lidí')
plt.xlabel('Počet lidí')
plt.ylabel('P(shoda narozenin)')
plt.title('Paradox narozenin')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
### Příklad 3: Spam filtr (Bayesova věta)
**Zadání**: E-mailový filtr analyzuje slova. Slovo "výhra" se vyskytuje v 80 % spamů a 1 % legitimních e-mailů. Spam tvoří 20 % všech e-mailů. Pokud e-mail obsahuje slovo "výhra", jaká je pravděpodobnost, že je spam?
**Řešení**:
```{python}
# Apriorní pravděpodobnosti
P_spam = 0.20
P_legitimni = 0.80
# Podmíněné pravděpodobnosti
P_vyhra_kdyz_spam = 0.80
P_vyhra_kdyz_legitimni = 0.01
# Celková pravděpodobnost slova "výhra"
P_vyhra = P_vyhra_kdyz_spam * P_spam + P_vyhra_kdyz_legitimni * P_legitimni
# Bayesova věta
P_spam_kdyz_vyhra = (P_vyhra_kdyz_spam * P_spam) / P_vyhra
print("Spam filtr - Bayesova věta")
print("=" * 40)
print(f"P(spam) = {P_spam:.0%}")
print(f"P('výhra' | spam) = {P_vyhra_kdyz_spam:.0%}")
print(f"P('výhra' | legitimní) = {P_vyhra_kdyz_legitimni:.0%}")
print(f"\nP('výhra') = {P_vyhra:.4f}")
print(f"P(spam | 'výhra') = {P_spam_kdyz_vyhra:.2%}")
```
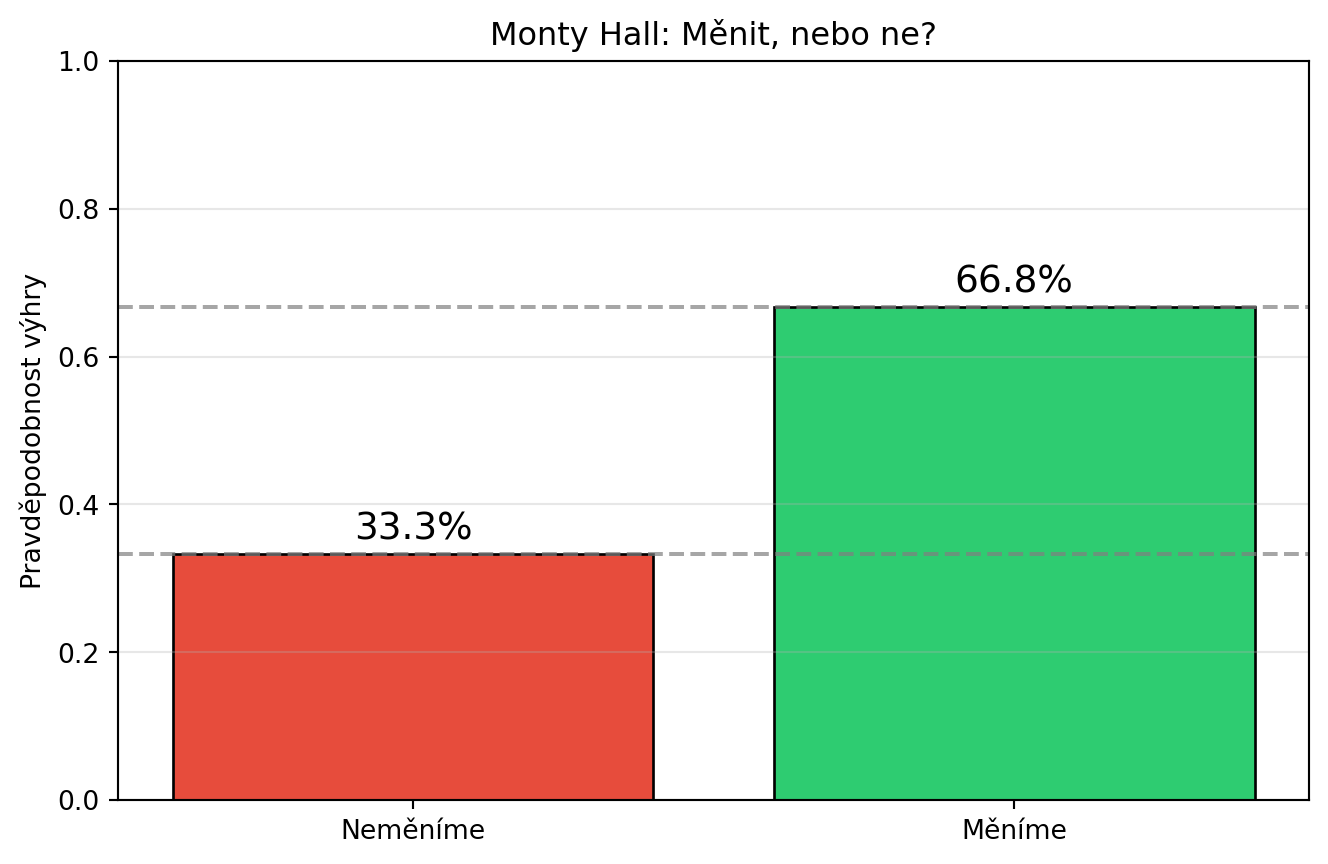
### Příklad 4: Monty Hall problém
**Zadání**: V soutěži jsou troje dveře. Za jedněmi je auto, za zbylými kozy. Vyberete dveře, moderátor (který ví, kde je auto) otevře jiné dveře s kozou a nabídne vám změnu. Máte změnit výběr?
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
def simulace_monty_hall(zmenime, n_her=10000):
"""Simulace Monty Hall problému."""
vyhry = 0
for _ in range(n_her):
# Náhodné umístění auta (0, 1, nebo 2)
auto = np.random.randint(0, 3)
# Náš první výběr
vyber = np.random.randint(0, 3)
# Moderátor otevře dveře s kozou (ne naše, ne s autem)
moznosti = [d for d in range(3) if d != vyber and d != auto]
otevrene = np.random.choice(moznosti)
# Pokud měníme, vybereme zbývající dveře
if zmenime:
novy_vyber = [d for d in range(3) if d != vyber and d != otevrene][0]
vyber = novy_vyber
if vyber == auto:
vyhry += 1
return vyhry / n_her
P_vyhra_nemenime = simulace_monty_hall(zmenime=False)
P_vyhra_menime = simulace_monty_hall(zmenime=True)
print("Monty Hall problém - simulace")
print("=" * 40)
print(f"P(výhra | neměníme) = {P_vyhra_nemenime:.4f} ≈ 1/3")
print(f"P(výhra | měníme) = {P_vyhra_menime:.4f} ≈ 2/3")
print(f"\n→ Vždy bychom měli změnit výběr!")
# Vizualizace
fig, ax = plt.subplots(figsize=(8, 5))
strategie = ['Neměníme', 'Měníme']
vysledky = [P_vyhra_nemenime, P_vyhra_menime]
colors = ['#e74c3c', '#2ecc71']
bars = ax.bar(strategie, vysledky, color=colors, edgecolor='black')
ax.axhline(y=1/3, color='gray', linestyle='--', alpha=0.7)
ax.axhline(y=2/3, color='gray', linestyle='--', alpha=0.7)
ax.set_ylabel('Pravděpodobnost výhry')
ax.set_title('Monty Hall: Měnit, nebo ne?')
ax.set_ylim(0, 1)
for bar, val in zip(bars, vysledky):
ax.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.02,
f'{val:.1%}', ha='center', fontsize=14)
plt.grid(axis='y', alpha=0.3)
plt.show()
```
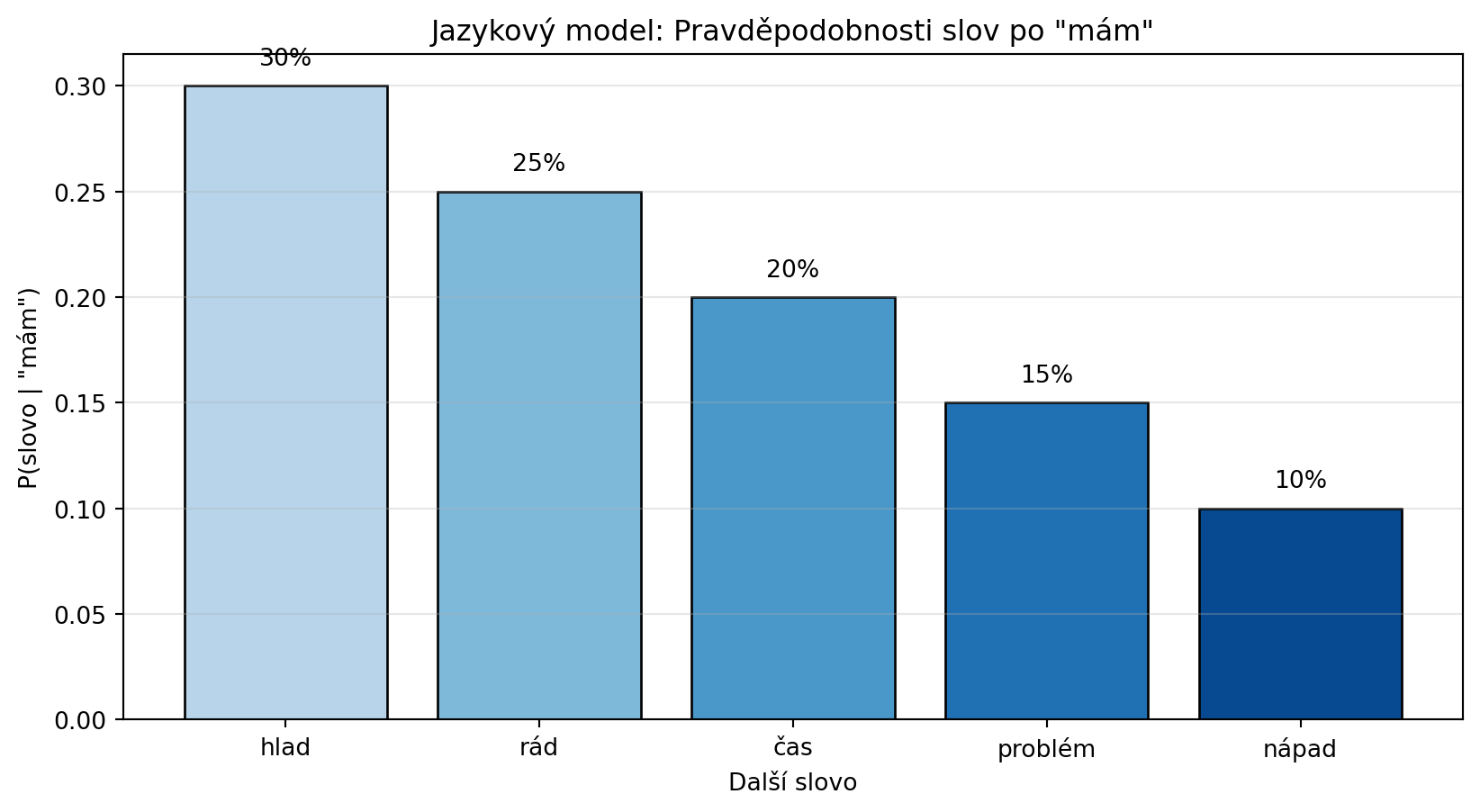
### Příklad 5: Jazykový model - predikce slova
**Zadání**: Máme zjednodušený jazykový model. Spočítejte pravděpodobnosti dalšího slova v sekvenci.
**Řešení**:
```{python}
# Jednoduchý bigramový model natrénovaný na textu
# P(slovo | předchozí slovo)
import numpy as np
import matplotlib.pyplot as plt
bigramy = {
"já": {"jsem": 0.4, "mám": 0.3, "chci": 0.2, "nevím": 0.1},
"jsem": {"rád": 0.3, "unavený": 0.2, "doma": 0.2, "student": 0.15, "tady": 0.15},
"mám": {"hlad": 0.3, "rád": 0.25, "čas": 0.2, "problém": 0.15, "nápad": 0.1},
}
def predikce(predchozi_slovo):
"""Predikuje další slovo na základě předchozího."""
if predchozi_slovo not in bigramy:
return None
distribuce = bigramy[predchozi_slovo]
slova = list(distribuce.keys())
pravdepodobnosti = list(distribuce.values())
return slova, pravdepodobnosti
# Příklad: Co následuje po "mám"?
predchozi = "mám"
slova, probs = predikce(predchozi)
print(f"Predikce pro slovo po '{predchozi}':")
for slovo, p in sorted(zip(slova, probs), key=lambda x: -x[1]):
print(f" P({slovo} | {predchozi}) = {p:.2f}")
# Vizualizace
plt.figure(figsize=(10, 5))
colors = plt.cm.Blues(np.linspace(0.3, 0.9, len(slova)))
bars = plt.bar(slova, probs, color=colors, edgecolor='black')
plt.xlabel('Další slovo')
plt.ylabel(f'P(slovo | "{predchozi}")')
plt.title(f'Jazykový model: Pravděpodobnosti slov po "{predchozi}"')
for bar, p in zip(bars, probs):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.01,
f'{p:.0%}', ha='center')
plt.grid(axis='y', alpha=0.3)
plt.show()
```
### Příklad 6: Řetězec pravděpodobností
**Zadání**: Jaká je pravděpodobnost věty "já mám hlad" v našem bigramovém modelu?
**Řešení**:
```{python}
# P("já mám hlad") = P("já") * P("mám"|"já") * P("hlad"|"mám")
# Předpokládáme P("já") na začátku věty
P_ja = 0.15 # Přibližný odhad
P_mam_kdyz_ja = bigramy["já"]["mám"]
P_hlad_kdyz_mam = bigramy["mám"]["hlad"]
P_veta = P_ja * P_mam_kdyz_ja * P_hlad_kdyz_mam
print("Pravděpodobnost věty 'já mám hlad':")
print(f"P('já') × P('mám'|'já') × P('hlad'|'mám')")
print(f"= {P_ja} × {P_mam_kdyz_ja} × {P_hlad_kdyz_mam}")
print(f"= {P_veta:.6f}")
print(f"\nToto je princip, jak jazykové modely hodnotí věty!")
```
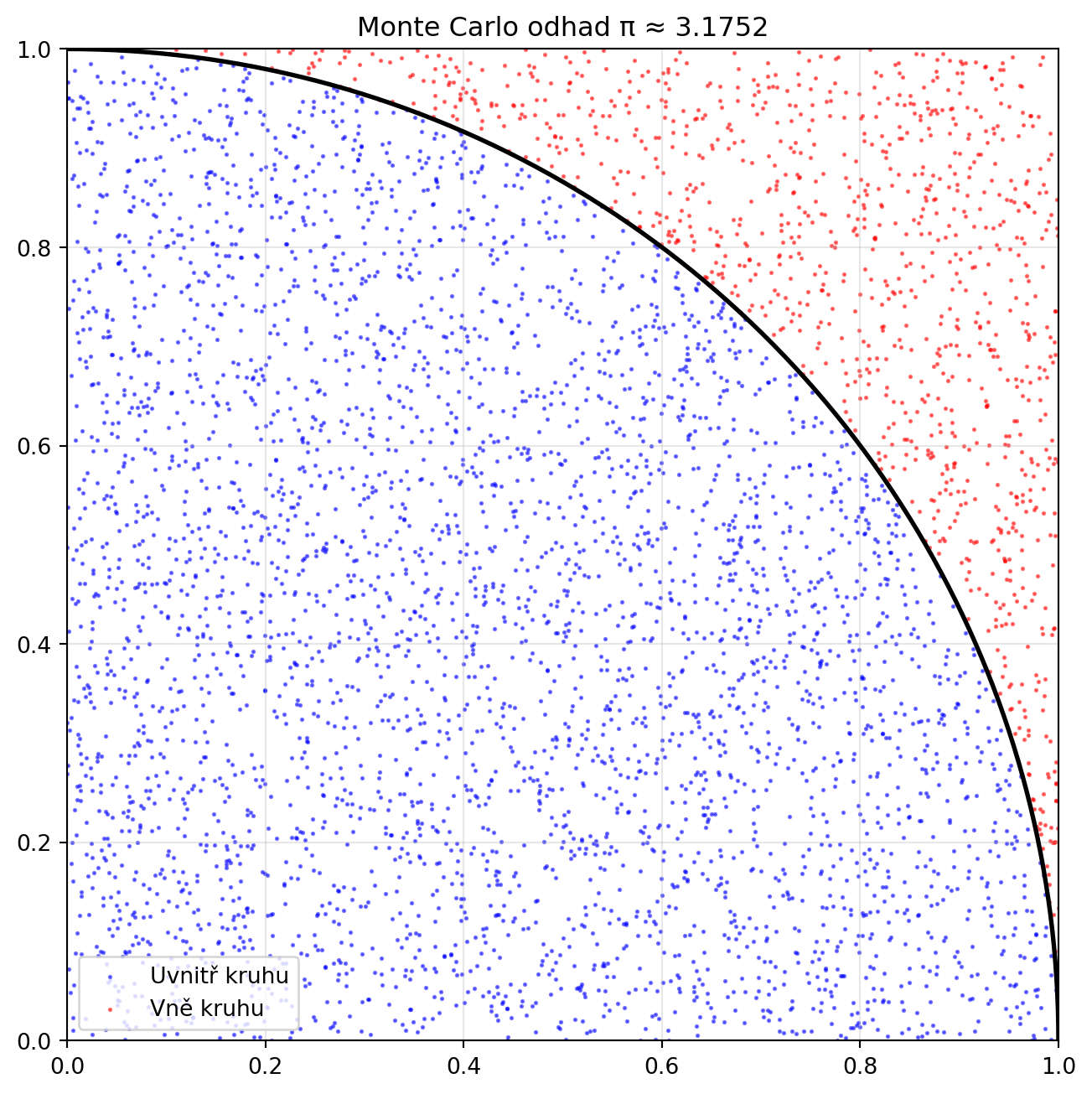
## Python v praxi: Simulace a Monte Carlo
Monte Carlo metody využívají náhodnost k řešení problémů:
```{python}
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
def monte_carlo_pi(n_bodu=10000):
"""Odhad čísla π pomocí Monte Carlo simulace."""
# Náhodné body v jednotkovém čtverci
x = np.random.uniform(0, 1, n_bodu)
y = np.random.uniform(0, 1, n_bodu)
# Kolik bodů padlo do čtvrtiny kruhu?
vzdalenost = x**2 + y**2
uvnitr = vzdalenost <= 1
# Poměr plochy čtvrtkruhu k ploše čtverce = π/4
pi_odhad = 4 * np.sum(uvnitr) / n_bodu
return pi_odhad, x, y, uvnitr
pi_odhad, x, y, uvnitr = monte_carlo_pi(5000)
print(f"Odhad π = {pi_odhad:.6f}")
print(f"Skutečné π = {np.pi:.6f}")
print(f"Chyba: {abs(pi_odhad - np.pi):.6f}")
# Vizualizace
plt.figure(figsize=(8, 8))
plt.scatter(x[uvnitr], y[uvnitr], c='blue', s=1, alpha=0.5, label='Uvnitř kruhu')
plt.scatter(x[~uvnitr], y[~uvnitr], c='red', s=1, alpha=0.5, label='Vně kruhu')
theta = np.linspace(0, np.pi/2, 100)
plt.plot(np.cos(theta), np.sin(theta), 'k-', lw=2)
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.gca().set_aspect('equal')
plt.legend()
plt.title(f'Monte Carlo odhad π ≈ {pi_odhad:.4f}')
plt.grid(True, alpha=0.3)
plt.show()
```
## Cvičení
::: {.callout-note icon=false}
## Cvičení 1: Kostky
Házíte dvěma kostkami. Jaká je pravděpodobnost, že:
a) Součet je větší než 9?
b) Alespoň jedna kostka ukáže 6?
c) Obě kostky ukáží stejné číslo?
:::
::: {.callout-note icon=false}
## Cvičení 2: Karty
Z balíčku 52 karet táhnete dvě karty bez vracení. Jaká je pravděpodobnost, že obě jsou esa?
:::
::: {.callout-note icon=false}
## Cvičení 3: Test na drogy
Test na drogy má senzitivitu 99 % a specificitu 95 %. V populaci užívá drogy 0.5 % lidí. Pokud je test pozitivní, jaká je pravděpodobnost, že osoba skutečně užívá drogy?
:::
::: {.callout-note icon=false}
## Cvičení 4: Tři dveře
Modifikujte Monty Hall problém: Je 4 dveří, za jedněmi auto, za zbylými kozy. Moderátor otevře dvoje dveře s kozami. Jaká je pravděpodobnost výhry při změně výběru? Ověřte simulací.
:::
::: {.callout-note icon=false}
## Cvičení 5: Bigramový model
Rozšiřte bigramový model o další slova a implementujte generování náhodných vět pomocí vzorkování z podmíněných pravděpodobností.
:::
::: {.callout-note icon=false}
## Cvičení 6: Monte Carlo
Použijte Monte Carlo metodu k odhadu pravděpodobnosti, že náhodný bod v jednotkovém čtverci má vzdálenost od středu menší než 0.3.
:::
## Shrnutí
::: {.callout-tip}
## Co jsme se naučili
1. **Pravděpodobnost** je číslo mezi 0 a 1 vyjadřující šanci, že událost nastane
2. **Pravidlo součtu**: $P(A \cup B) = P(A) + P(B) - P(A \cap B)$
3. **Pravidlo součinu**: $P(A \cap B) = P(A) \cdot P(B|A)$
4. **Podmíněná pravděpodobnost**: $P(A|B) = \frac{P(A \cap B)}{P(B)}$
5. **Bayesova věta** aktualizuje pravděpodobnosti na základě nových důkazů
6. **Nezávislost** znamená, že $P(A \cap B) = P(A) \cdot P(B)$
7. **Jazykové modely** používají podmíněné pravděpodobnosti pro predikci slov
:::
::: {.callout-important}
## Klíčové pojmy
- **Pravděpodobnost**: $P(A) \in [0, 1]$
- **Podmíněná pravděpodobnost**: $P(A|B)$
- **Bayesova věta**: $P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}$
- **Nezávislost**: $P(A \cap B) = P(A) \cdot P(B)$
- **Monte Carlo**: Odhad pomocí náhodného vzorkování
:::
Pravděpodobnost je základem pro pochopení nejistoty v datech a modelech. V dalších kapitolách se podíváme na náhodné veličiny a rozdělení pravděpodobnosti, které nám umožní pracovat s pravděpodobností systematičtěji.