# Lineární transformace
::: {.callout-tip title="Co se naučíte"}
V této kapitole se naučíte:
- Chápat matice jako transformace
- Základní transformace: rotace, škálování, zrcadlení
- Jak skládat transformace
- Vizualizovat efekt matic
:::
## Matice jako transformace
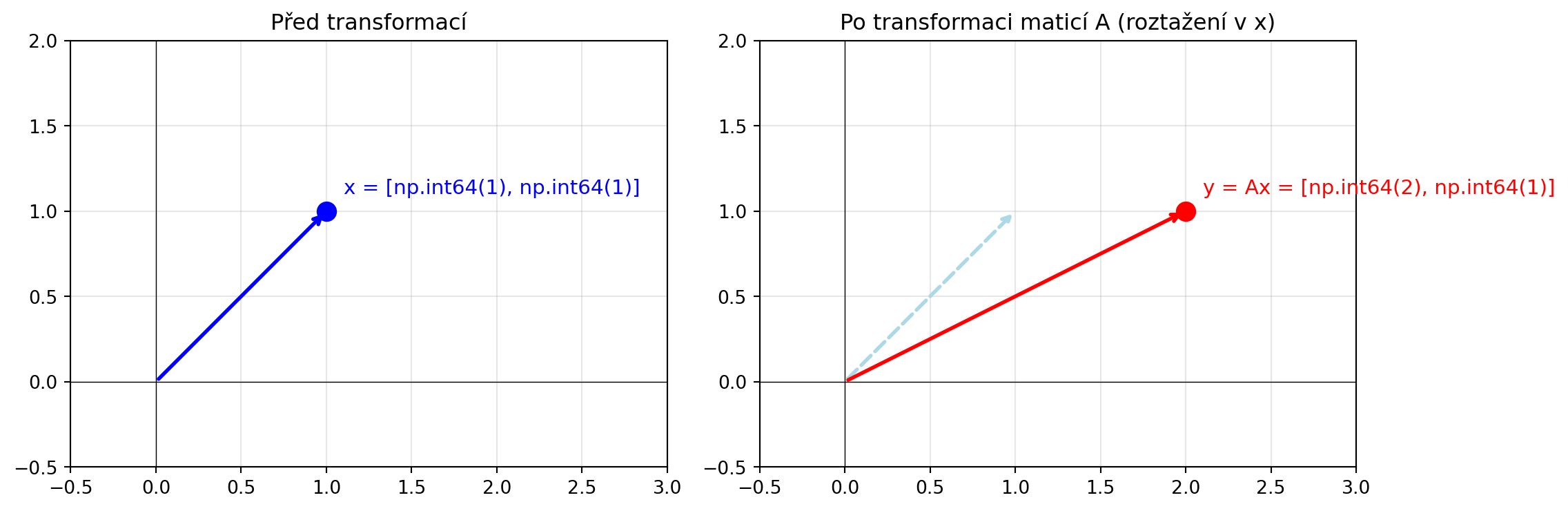
Každá matice reprezentuje **transformaci** -- přeměnu jednoho vektoru na jiný. Když vynásobíme vektor maticí, "transformujeme" ho.
$$\mathbf{y} = \mathbf{A}\mathbf{x}$$
Vstup $\mathbf{x}$ se změní na výstup $\mathbf{y}$.
```{python}
import numpy as np
import matplotlib.pyplot as plt
# Transformační matice
A = np.array([
[2, 0],
[0, 1]
])
# Vstupní vektor
x = np.array([1, 1])
# Transformovaný vektor
y = A @ x
print(f"Vstup x: {x}")
print(f"Matice A:\n{A}")
print(f"Výstup y = Ax: {y}")
```
```{python}
#| fig-cap: "Matice jako transformace"
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
# Původní vektor
axes[0].annotate('', xy=x, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='blue', lw=2))
axes[0].plot(*x, 'bo', markersize=10)
axes[0].text(x[0]+0.1, x[1]+0.1, f'x = {list(x)}', fontsize=11, color='blue')
axes[0].set_xlim(-0.5, 3)
axes[0].set_ylim(-0.5, 2)
axes[0].set_aspect('equal')
axes[0].grid(True, alpha=0.3)
axes[0].axhline(y=0, color='k', linewidth=0.5)
axes[0].axvline(x=0, color='k', linewidth=0.5)
axes[0].set_title('Před transformací')
# Transformovaný vektor
axes[1].annotate('', xy=x, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='lightblue', lw=2, linestyle='--'))
axes[1].annotate('', xy=y, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='red', lw=2))
axes[1].plot(*y, 'ro', markersize=10)
axes[1].text(y[0]+0.1, y[1]+0.1, f'y = Ax = {list(y)}', fontsize=11, color='red')
axes[1].set_xlim(-0.5, 3)
axes[1].set_ylim(-0.5, 2)
axes[1].set_aspect('equal')
axes[1].grid(True, alpha=0.3)
axes[1].axhline(y=0, color='k', linewidth=0.5)
axes[1].axvline(x=0, color='k', linewidth=0.5)
axes[1].set_title('Po transformaci maticí A (roztažení v x)')
plt.tight_layout()
plt.show()
```
---
## Základní transformace
### Škálování
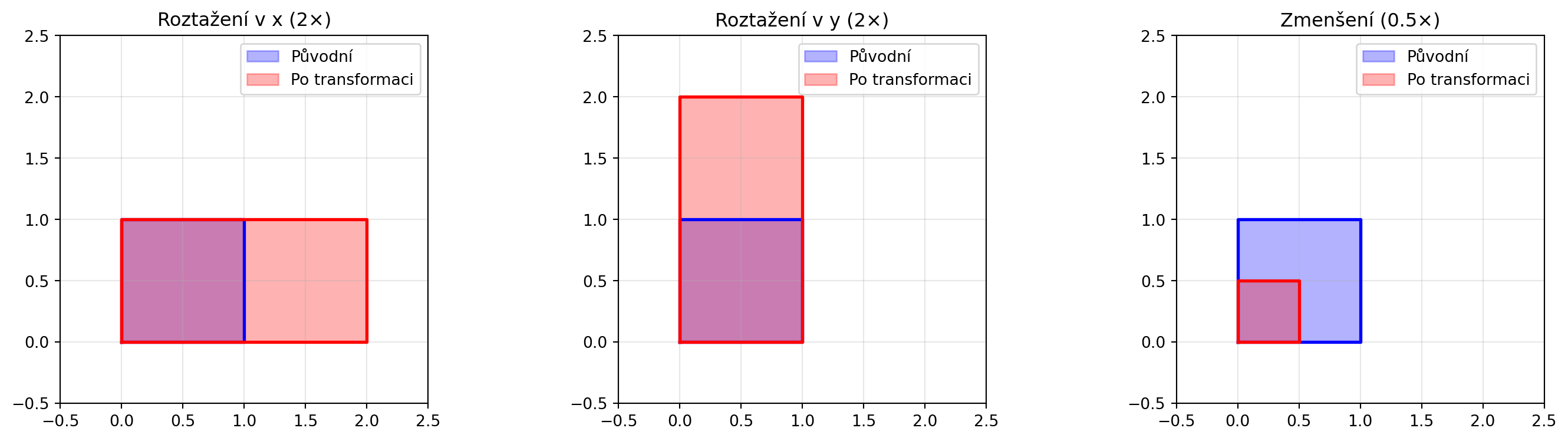
**Škálování** mění velikost vektoru v jednotlivých osách:
$$\mathbf{S} = \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix}$$
```{python}
#| fig-cap: "Škálování"
#| code-fold: true
import numpy as np
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# Původní čtverec
original = np.array([[0, 0], [1, 0], [1, 1], [0, 1], [0, 0]]).T
skalovani = [
(np.array([[2, 0], [0, 1]]), "Roztažení v x (2×)"),
(np.array([[1, 0], [0, 2]]), "Roztažení v y (2×)"),
(np.array([[0.5, 0], [0, 0.5]]), "Zmenšení (0.5×)")
]
for ax, (S, title) in zip(axes, skalovani):
transformed = S @ original
ax.fill(original[0], original[1], alpha=0.3, color='blue', label='Původní')
ax.fill(transformed[0], transformed[1], alpha=0.3, color='red', label='Po transformaci')
ax.plot(original[0], original[1], 'b-', linewidth=2)
ax.plot(transformed[0], transformed[1], 'r-', linewidth=2)
ax.set_xlim(-0.5, 2.5)
ax.set_ylim(-0.5, 2.5)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.legend()
ax.set_title(title)
plt.tight_layout()
plt.show()
```
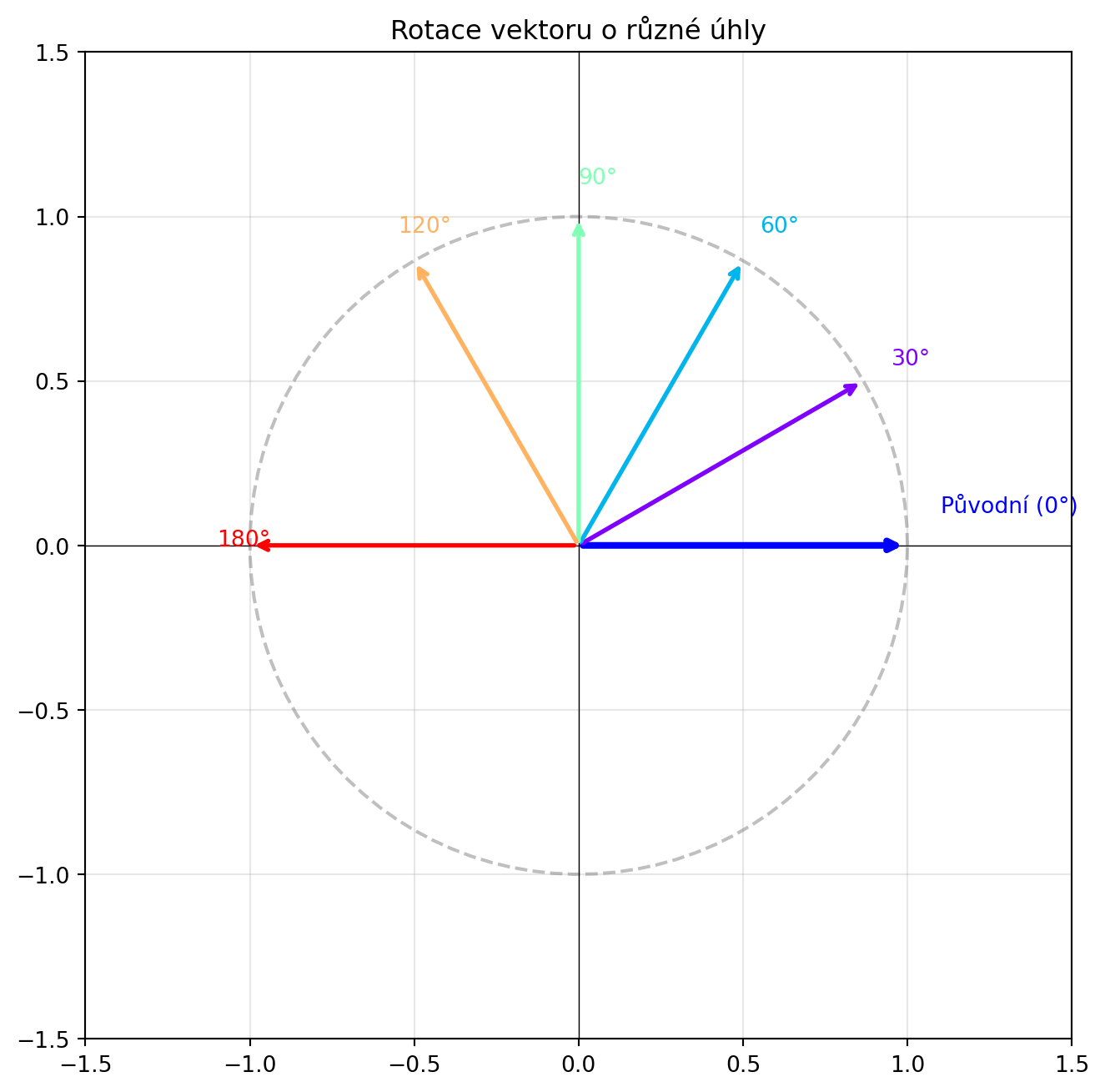
### Rotace
**Rotace** otáčí vektor o úhel $\theta$:
$$\mathbf{R}(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}$$
```{python}
import numpy as np
def rotacni_matice(uhel_stupne):
"""Vytvoří rotační matici pro daný úhel ve stupních."""
theta = np.radians(uhel_stupne)
return np.array([
[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]
])
# Rotace o 45°
R45 = rotacni_matice(45)
print("Rotační matice pro 45°:")
print(R45.round(3))
# Aplikace na vektor
v = np.array([1, 0])
v_rotovany = R45 @ v
print(f"\nVektor [1, 0] po rotaci o 45°: {v_rotovany.round(3)}")
```
```{python}
#| fig-cap: "Rotace o různé úhly"
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 8))
# Původní vektor
v = np.array([1, 0])
ax.annotate('', xy=v, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='blue', lw=3))
ax.text(v[0]+0.1, v[1]+0.1, 'Původní (0°)', color='blue', fontsize=10)
# Rotace o různé úhly
uhly = [30, 60, 90, 120, 180]
barvy = plt.cm.rainbow(np.linspace(0, 1, len(uhly)))
for uhel, barva in zip(uhly, barvy):
R = rotacni_matice(uhel)
v_rot = R @ v
ax.annotate('', xy=v_rot, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color=barva, lw=2))
ax.text(v_rot[0]*1.1, v_rot[1]*1.1, f'{uhel}°', fontsize=10, color=barva)
# Jednotková kružnice
theta = np.linspace(0, 2*np.pi, 100)
ax.plot(np.cos(theta), np.sin(theta), 'gray', linestyle='--', alpha=0.5)
ax.set_xlim(-1.5, 1.5)
ax.set_ylim(-1.5, 1.5)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='k', linewidth=0.5)
ax.axvline(x=0, color='k', linewidth=0.5)
ax.set_title('Rotace vektoru o různé úhly')
plt.show()
```
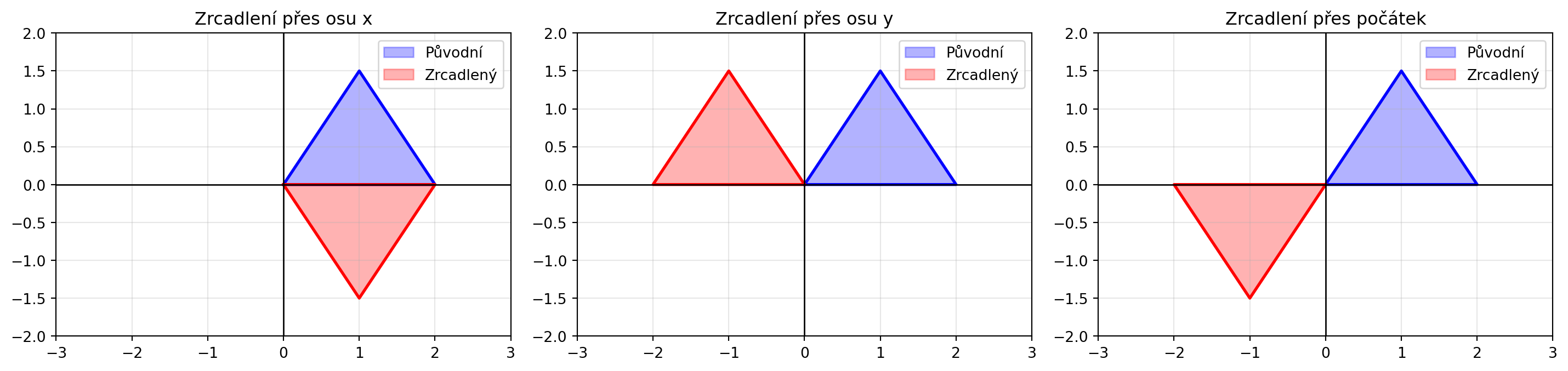
### Zrcadlení
**Zrcadlení** převrací body přes osu:
```{python}
# Zrcadlení přes osu x
import numpy as np
Mx = np.array([[1, 0], [0, -1]])
# Zrcadlení přes osu y
My = np.array([[-1, 0], [0, 1]])
# Zrcadlení přes počátek
Mo = np.array([[-1, 0], [0, -1]])
print("Zrcadlení přes osu x (y → -y):")
print(Mx)
print("\nZrcadlení přes osu y (x → -x):")
print(My)
```
```{python}
#| fig-cap: "Zrcadlení"
import numpy as np
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# Původní trojúhelník
original = np.array([[0, 0], [2, 0], [1, 1.5], [0, 0]]).T
zrcadleni = [
(np.array([[1, 0], [0, -1]]), "Zrcadlení přes osu x"),
(np.array([[-1, 0], [0, 1]]), "Zrcadlení přes osu y"),
(np.array([[-1, 0], [0, -1]]), "Zrcadlení přes počátek")
]
for ax, (M, title) in zip(axes, zrcadleni):
transformed = M @ original
ax.fill(original[0], original[1], alpha=0.3, color='blue', label='Původní')
ax.fill(transformed[0], transformed[1], alpha=0.3, color='red', label='Zrcadlený')
ax.plot(original[0], original[1], 'b-', linewidth=2)
ax.plot(transformed[0], transformed[1], 'r-', linewidth=2)
ax.set_xlim(-3, 3)
ax.set_ylim(-2, 2)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='k', linewidth=1)
ax.axvline(x=0, color='k', linewidth=1)
ax.legend(loc='upper right')
ax.set_title(title)
plt.tight_layout()
plt.show()
```
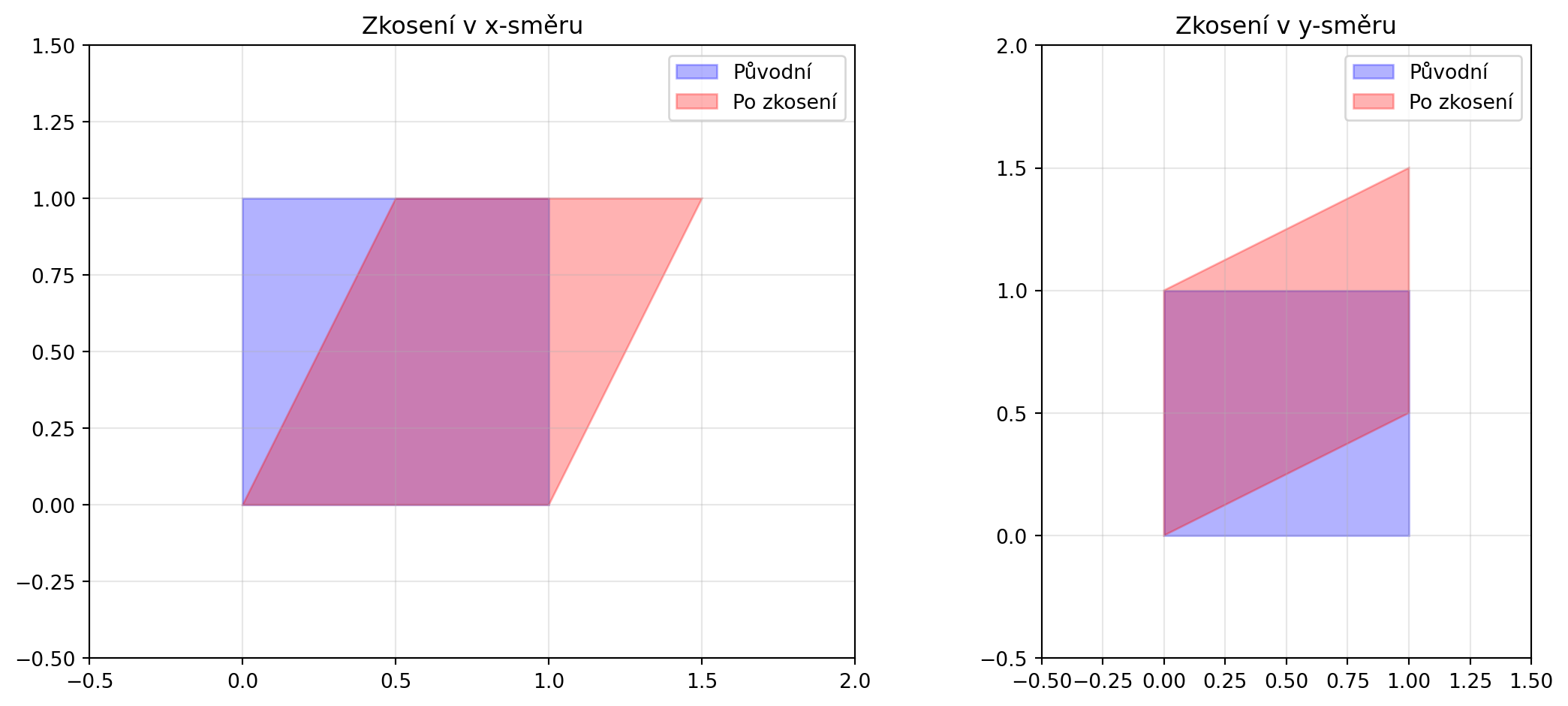
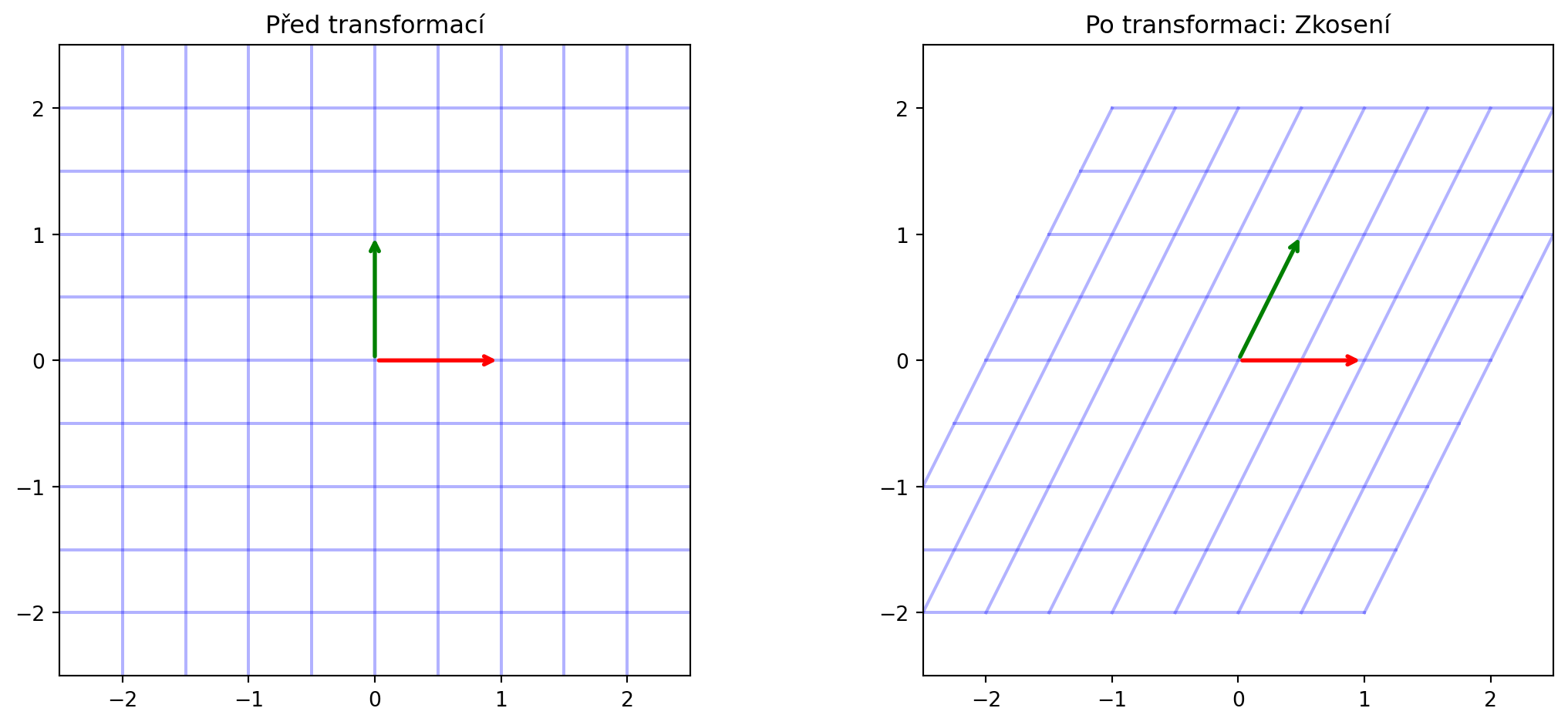
### Zkosení (shear)
**Zkosení** posunuje body v jednom směru proporcionálně k jejich pozici v druhém:
```{python}
#| fig-cap: "Zkosení"
import numpy as np
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
original = np.array([[0, 0], [1, 0], [1, 1], [0, 1], [0, 0]]).T
# Zkosení v x
Shx = np.array([[1, 0.5], [0, 1]])
trans_x = Shx @ original
axes[0].fill(original[0], original[1], alpha=0.3, color='blue', label='Původní')
axes[0].fill(trans_x[0], trans_x[1], alpha=0.3, color='red', label='Po zkosení')
axes[0].set_title('Zkosení v x-směru')
axes[0].legend()
axes[0].set_aspect('equal')
axes[0].grid(True, alpha=0.3)
axes[0].set_xlim(-0.5, 2)
axes[0].set_ylim(-0.5, 1.5)
# Zkosení v y
Shy = np.array([[1, 0], [0.5, 1]])
trans_y = Shy @ original
axes[1].fill(original[0], original[1], alpha=0.3, color='blue', label='Původní')
axes[1].fill(trans_y[0], trans_y[1], alpha=0.3, color='red', label='Po zkosení')
axes[1].set_title('Zkosení v y-směru')
axes[1].legend()
axes[1].set_aspect('equal')
axes[1].grid(True, alpha=0.3)
axes[1].set_xlim(-0.5, 1.5)
axes[1].set_ylim(-0.5, 2)
plt.tight_layout()
plt.show()
```
---
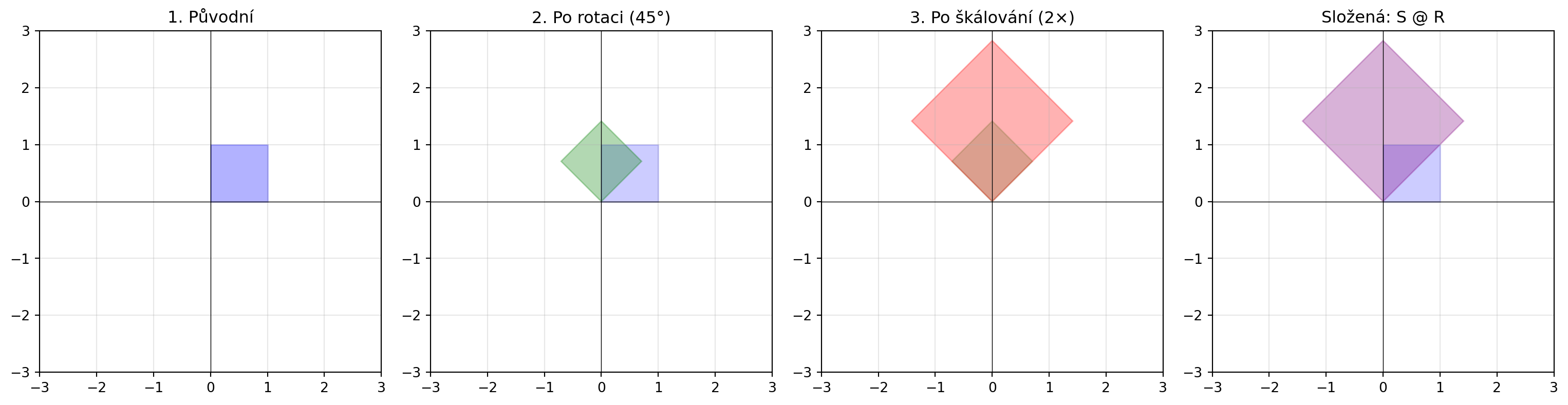
## Skládání transformací
Transformace můžeme skládat násobením matic. Pořadí je důležité!
$$\mathbf{C} = \mathbf{B} \cdot \mathbf{A}$$
Nejprve se aplikuje $\mathbf{A}$, pak $\mathbf{B}$.
```{python}
#| fig-cap: "Skládání transformací"
# Rotace o 45° + škálování 2×
import numpy as np
import matplotlib.pyplot as plt
R = rotacni_matice(45)
S = np.array([[2, 0], [0, 2]])
# Složená transformace
C = S @ R # Nejprve rotace, pak škálování
original = np.array([[0, 0], [1, 0], [1, 1], [0, 1], [0, 0]]).T
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
# Původní
axes[0].fill(original[0], original[1], alpha=0.3, color='blue')
axes[0].set_title('1. Původní')
# Po rotaci
rotated = R @ original
axes[1].fill(original[0], original[1], alpha=0.2, color='blue')
axes[1].fill(rotated[0], rotated[1], alpha=0.3, color='green')
axes[1].set_title('2. Po rotaci (45°)')
# Po škálování
scaled = S @ rotated
axes[2].fill(rotated[0], rotated[1], alpha=0.2, color='green')
axes[2].fill(scaled[0], scaled[1], alpha=0.3, color='red')
axes[2].set_title('3. Po škálování (2×)')
# Složená transformace najednou
combined = C @ original
axes[3].fill(original[0], original[1], alpha=0.2, color='blue')
axes[3].fill(combined[0], combined[1], alpha=0.3, color='purple')
axes[3].set_title('Složená: S @ R')
for ax in axes:
ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='k', linewidth=0.5)
ax.axvline(x=0, color='k', linewidth=0.5)
plt.tight_layout()
plt.show()
```
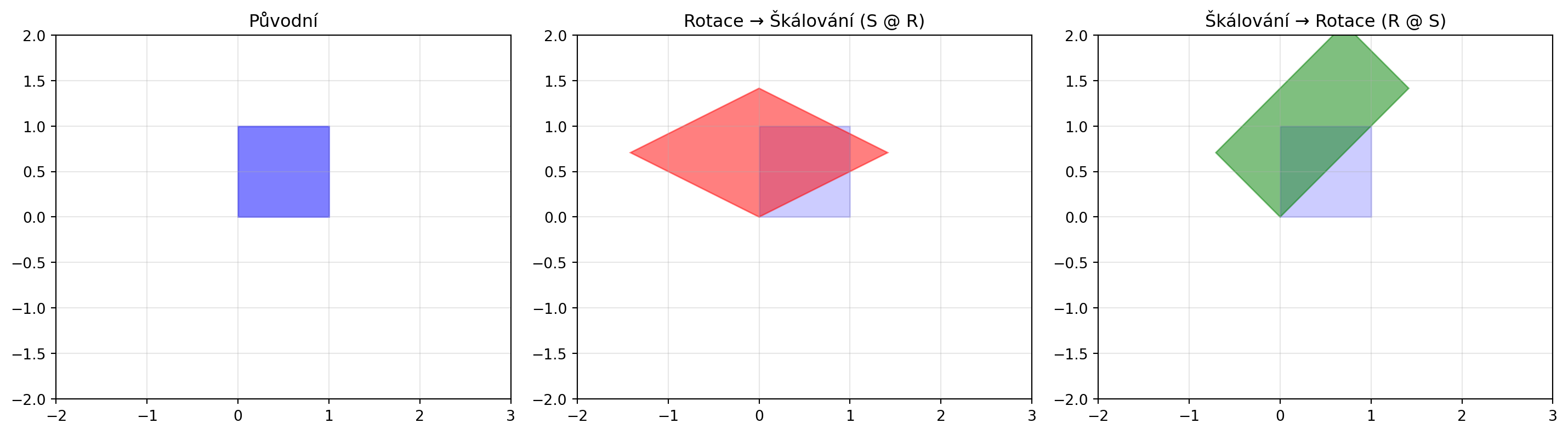
::: {.callout-warning title="Pořadí záleží!"}
Rotace + škálování ≠ Škálování + rotace
:::
```{python}
#| fig-cap: "Pořadí transformací záleží"
import numpy as np
import matplotlib.pyplot as plt
R = rotacni_matice(45)
S = np.array([[2, 0], [0, 1]]) # Nerovnoměrné škálování
original = np.array([[0, 0], [1, 0], [1, 1], [0, 1], [0, 0]]).T
# Různé pořadí
SR = S @ R # Nejprve rotace, pak škálování
RS = R @ S # Nejprve škálování, pak rotace
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
axes[0].fill(original[0], original[1], alpha=0.5, color='blue')
axes[0].set_title('Původní')
trans1 = SR @ original
axes[1].fill(original[0], original[1], alpha=0.2, color='blue')
axes[1].fill(trans1[0], trans1[1], alpha=0.5, color='red')
axes[1].set_title('Rotace → Škálování (S @ R)')
trans2 = RS @ original
axes[2].fill(original[0], original[1], alpha=0.2, color='blue')
axes[2].fill(trans2[0], trans2[1], alpha=0.5, color='green')
axes[2].set_title('Škálování → Rotace (R @ S)')
for ax in axes:
ax.set_xlim(-2, 3)
ax.set_ylim(-2, 2)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
---
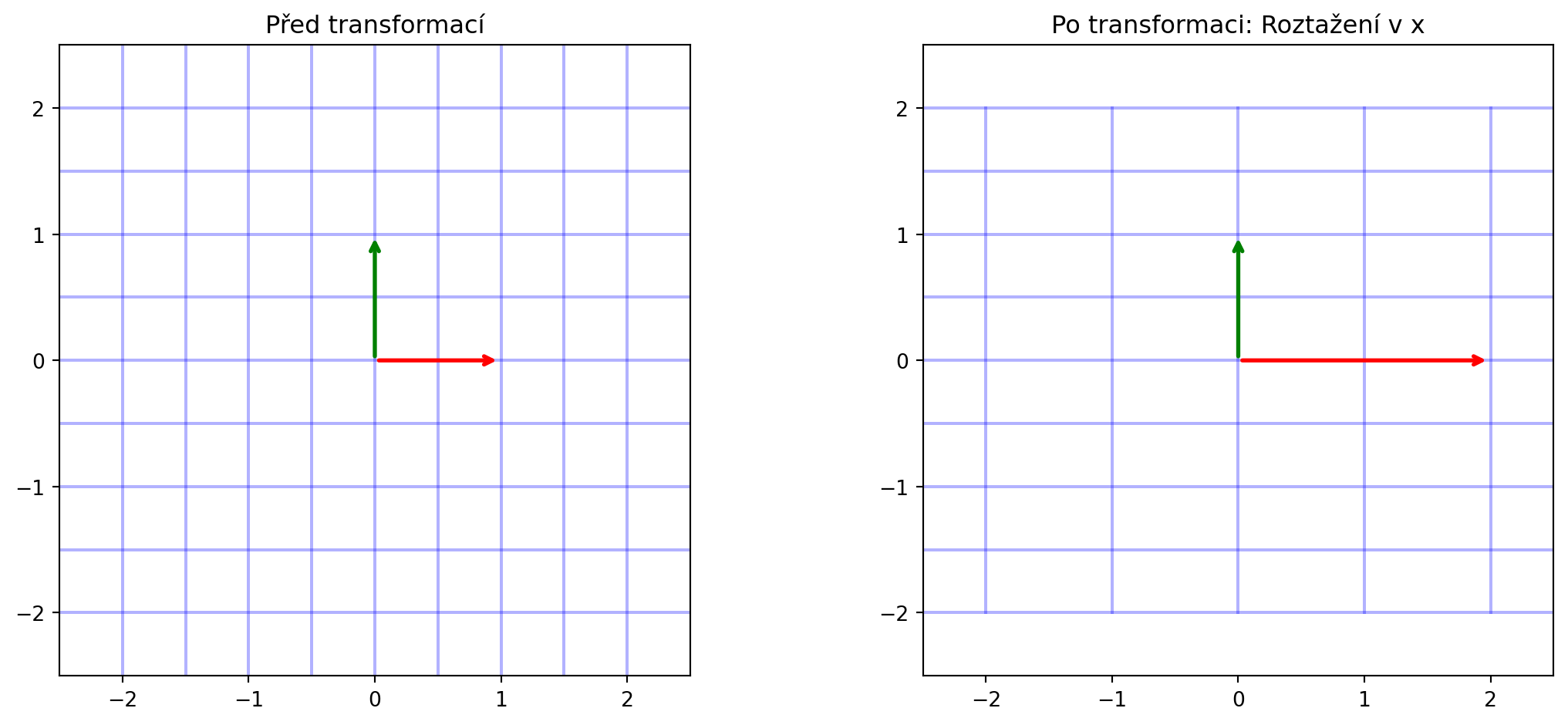
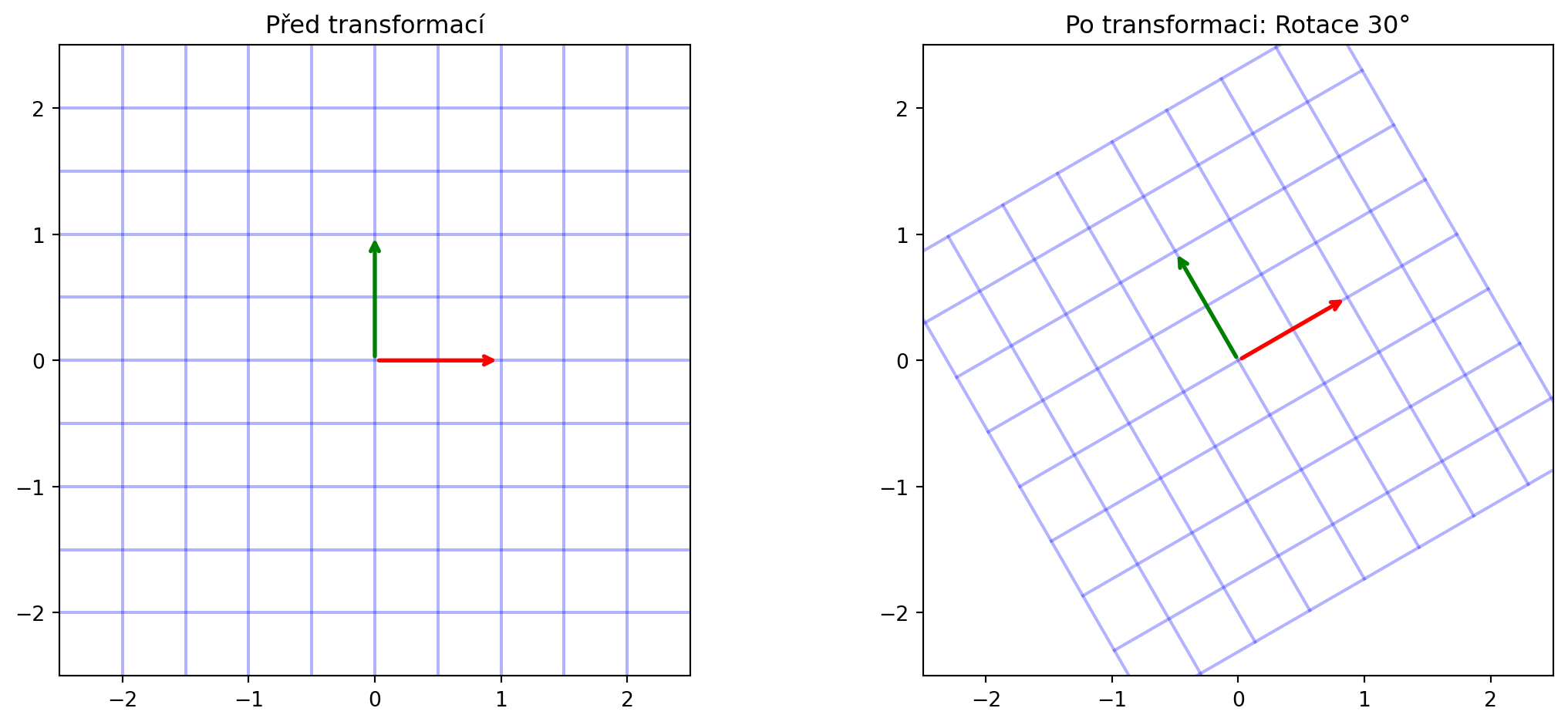
## Vizualizace efektu matice
Užitečný způsob, jak pochopit matici, je vidět, co dělá s mřížkou:
```{python}
#| fig-cap: "Efekt matice na mřížku"
import numpy as np
import matplotlib.pyplot as plt
def vizualizuj_transformaci(A, title="Transformace"):
"""Vizualizuje efekt matice na mřížce."""
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
# Původní mřížka
for i in np.linspace(-2, 2, 9):
axes[0].axhline(y=i, color='blue', alpha=0.3)
axes[0].axvline(x=i, color='blue', alpha=0.3)
# Jednotkové vektory
axes[0].annotate('', xy=(1, 0), xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='red', lw=2))
axes[0].annotate('', xy=(0, 1), xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='green', lw=2))
axes[0].set_xlim(-2.5, 2.5)
axes[0].set_ylim(-2.5, 2.5)
axes[0].set_aspect('equal')
axes[0].set_title('Před transformací')
# Transformovaná mřížka
for i in np.linspace(-2, 2, 9):
# Horizontální čáry
line = np.array([[-2, i], [2, i]]).T
trans_line = A @ line
axes[1].plot(trans_line[0], trans_line[1], 'blue', alpha=0.3)
# Vertikální čáry
line = np.array([[i, -2], [i, 2]]).T
trans_line = A @ line
axes[1].plot(trans_line[0], trans_line[1], 'blue', alpha=0.3)
# Transformované jednotkové vektory
e1 = A @ np.array([1, 0])
e2 = A @ np.array([0, 1])
axes[1].annotate('', xy=e1, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='red', lw=2))
axes[1].annotate('', xy=e2, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='green', lw=2))
axes[1].set_xlim(-2.5, 2.5)
axes[1].set_ylim(-2.5, 2.5)
axes[1].set_aspect('equal')
axes[1].set_title(f'Po transformaci: {title}')
plt.tight_layout()
plt.show()
# Ukázky
vizualizuj_transformaci(np.array([[2, 0], [0, 1]]), "Roztažení v x")
vizualizuj_transformaci(rotacni_matice(30), "Rotace 30°")
vizualizuj_transformaci(np.array([[1, 0.5], [0, 1]]), "Zkosení")
```
---
## Aplikace
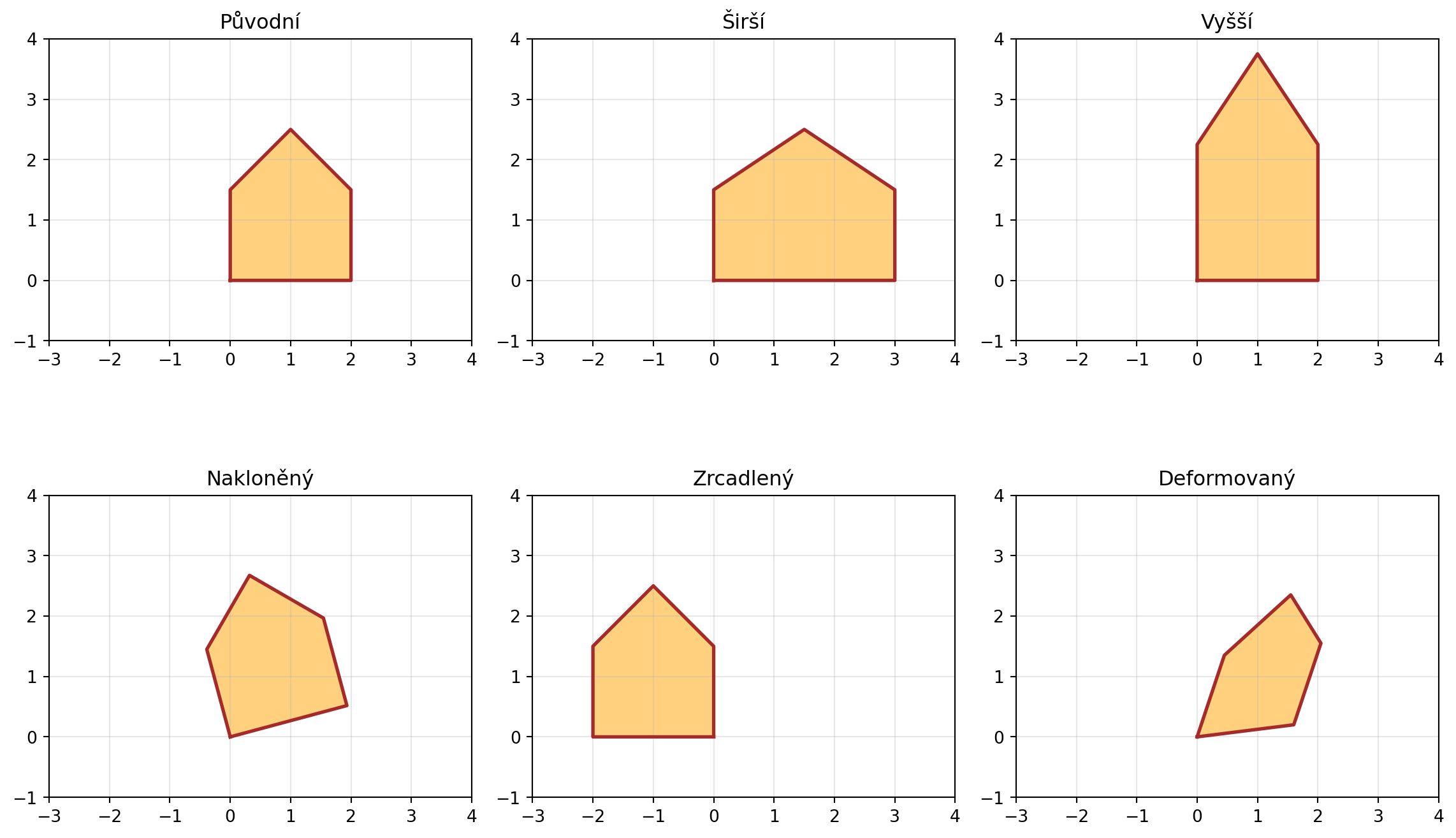
### Transformace v grafice
```{python}
#| fig-cap: "Animace transformací"
# Jednoduchý domeček
import numpy as np
import matplotlib.pyplot as plt
dum = np.array([
[0, 0], # levý dolní
[2, 0], # pravý dolní
[2, 1.5], # pravý horní
[1, 2.5], # špička střechy
[0, 1.5], # levý horní
[0, 0] # zpět na začátek
]).T
fig, axes = plt.subplots(2, 3, figsize=(12, 8))
axes = axes.flatten()
transformace = [
(np.eye(2), "Původní"),
(np.array([[1.5, 0], [0, 1]]), "Širší"),
(np.array([[1, 0], [0, 1.5]]), "Vyšší"),
(rotacni_matice(15), "Nakloněný"),
(np.array([[-1, 0], [0, 1]]), "Zrcadlený"),
(np.array([[0.8, 0.3], [0.1, 0.9]]), "Deformovaný")
]
for ax, (T, title) in zip(axes, transformace):
trans_dum = T @ dum
ax.fill(trans_dum[0], trans_dum[1], alpha=0.5, color='orange')
ax.plot(trans_dum[0], trans_dum[1], 'brown', linewidth=2)
ax.set_xlim(-3, 4)
ax.set_ylim(-1, 4)
ax.set_aspect('equal')
ax.set_title(title)
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
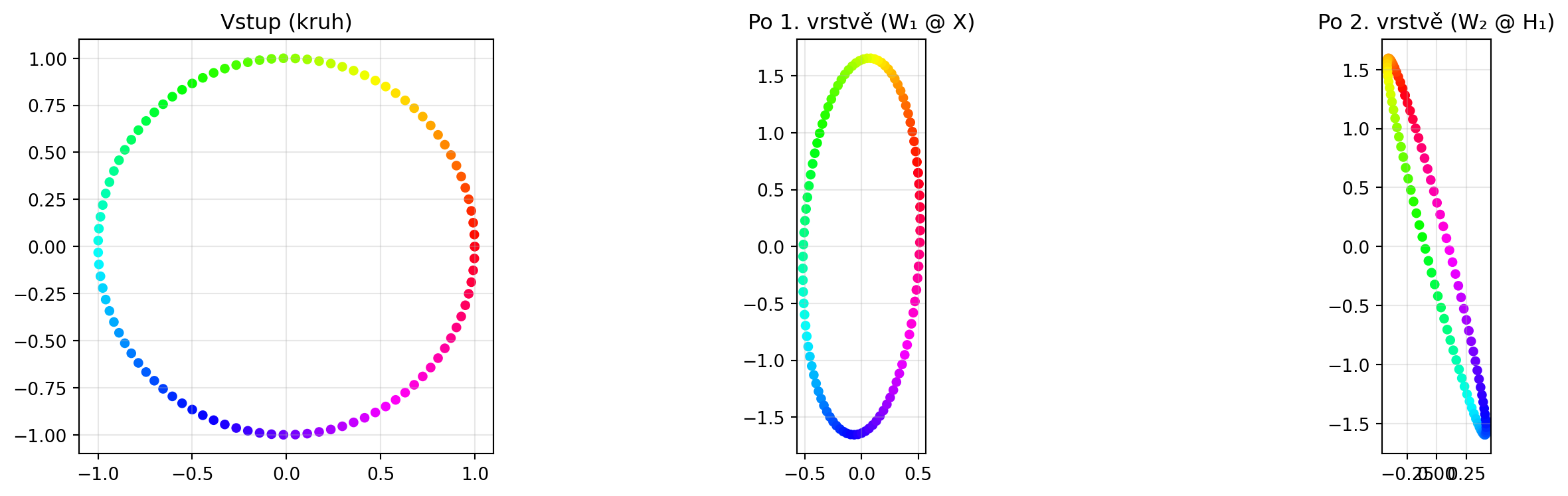
### Neuronová síť jako série transformací
```{python}
#| fig-cap: "Neuronová síť transformuje data"
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
# Vstupní data (kruh)
n = 100
theta = np.linspace(0, 2*np.pi, n)
X = np.vstack([np.cos(theta), np.sin(theta)])
# Váhy vrstev (náhodné matice)
W1 = np.random.randn(2, 2)
W2 = np.random.randn(2, 2)
# Transformace
H1 = W1 @ X
H2 = W2 @ H1
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
axes[0].scatter(X[0], X[1], c=theta, cmap='hsv', s=20)
axes[0].set_title('Vstup (kruh)')
axes[1].scatter(H1[0], H1[1], c=theta, cmap='hsv', s=20)
axes[1].set_title('Po 1. vrstvě (W₁ @ X)')
axes[2].scatter(H2[0], H2[1], c=theta, cmap='hsv', s=20)
axes[2].set_title('Po 2. vrstvě (W₂ @ H₁)')
for ax in axes:
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
---
## Řešené příklady
### Příklad 1: Rotace bodu
Otočte bod [3, 0] o 90° proti směru hodinových ručiček.
```{python}
import numpy as np
R90 = rotacni_matice(90)
bod = np.array([3, 0])
rotovany = R90 @ bod
print(f"Rotační matice pro 90°:\n{R90.round(3)}")
print(f"\nPůvodní bod: {bod}")
print(f"Po rotaci: {rotovany.round(3)}")
```
### Příklad 2: Složená transformace
Vytvořte matici, která nejprve zmenší na polovinu a pak otočí o 45°.
```{python}
import numpy as np
S = np.array([[0.5, 0], [0, 0.5]]) # Zmenšení
R = rotacni_matice(45) # Rotace
# Složená transformace (pozor na pořadí!)
C = R @ S # Nejprve S, pak R
print("Složená matice (rotace @ zmenšení):")
print(C.round(3))
# Test
bod = np.array([2, 0])
vysledek = C @ bod
print(f"\nBod [2, 0] po transformaci: {vysledek.round(3)}")
```
### Příklad 3: Identifikace transformace
Jakou transformaci provádí matice $\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$?
```{python}
import numpy as np
A = np.array([[0, -1], [1, 0]])
# Aplikujeme na jednotkové vektory
e1 = np.array([1, 0])
e2 = np.array([0, 1])
print(f"[1, 0] → {A @ e1}")
print(f"[0, 1] → {A @ e2}")
print("\nJde o rotaci o 90° proti směru hodinových ručiček!")
```
---
## Cvičení
::: {.callout-warning title="Cvičení 1: Škálovací matice"}
Vytvořte matici, která ztrojnásobí x-ovou souřadnici a zachová y-ovou.
**Výsledek:** $\begin{bmatrix} 3 & 0 \\ 0 & 1 \end{bmatrix}$
:::
::: {.callout-warning title="Cvičení 2: Rotace"}
Jaká je rotační matice pro 180°?
**Výsledek:** $\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}$
:::
::: {.callout-warning title="Cvičení 3: Identita transformace"}
Co dělá matice $\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$?
**Výsledek:** Zrcadlení přes osu x
:::
::: {.callout-warning title="Cvičení 4: Složená transformace"}
Jaká je matice pro zrcadlení přes osu y následované rotací o 90°?
<details>
<summary>Řešení</summary>
```python
import numpy as np
My = np.array([[-1, 0], [0, 1]])
R90 = rotacni_matice(90)
C = R90 @ My
print(C.round(3))
# Výsledek: [[0, 1], [1, 0]]
```
</details>
:::
::: {.callout-warning title="Cvičení 5: Inverzní transformace"}
Pokud matice R rotuje o 30°, jaká matice "vrátí" rotaci zpět?
**Odpověď:** Rotace o -30° (nebo transpozice R, protože rotační matice jsou ortogonální)
:::
---
## Shrnutí
::: {.callout-note title="Co si zapamatovat"}
- Každá matice reprezentuje **lineární transformaci**
- **Škálování**: $\begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix}$
- **Rotace o θ**: $\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}$
- **Zrcadlení přes x**: $\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$
- Transformace se **skládají** násobením matic
- Pořadí **záleží**: $\mathbf{AB} \neq \mathbf{BA}$
- Neuronové sítě jsou řetězce lineárních transformací + nelineární aktivace
:::
Dokončili jsme část o vektorech a maticích! V další části se ponoříme do **derivací a gradientů** -- matematického aparátu, který umožňuje neuronové sítě trénovat.