# Změna a rychlost změny
::: {.callout-tip title="Co se naučíte"}
V této kapitole se naučíte:
- Co je průměrná rychlost změny
- Co je okamžitá rychlost změny (derivace)
- Geometrickou interpretaci derivace
- Jak numericky aproximovat derivaci
- Proč jsou derivace klíčové pro strojové učení
:::
## Proč potřebujeme derivace?
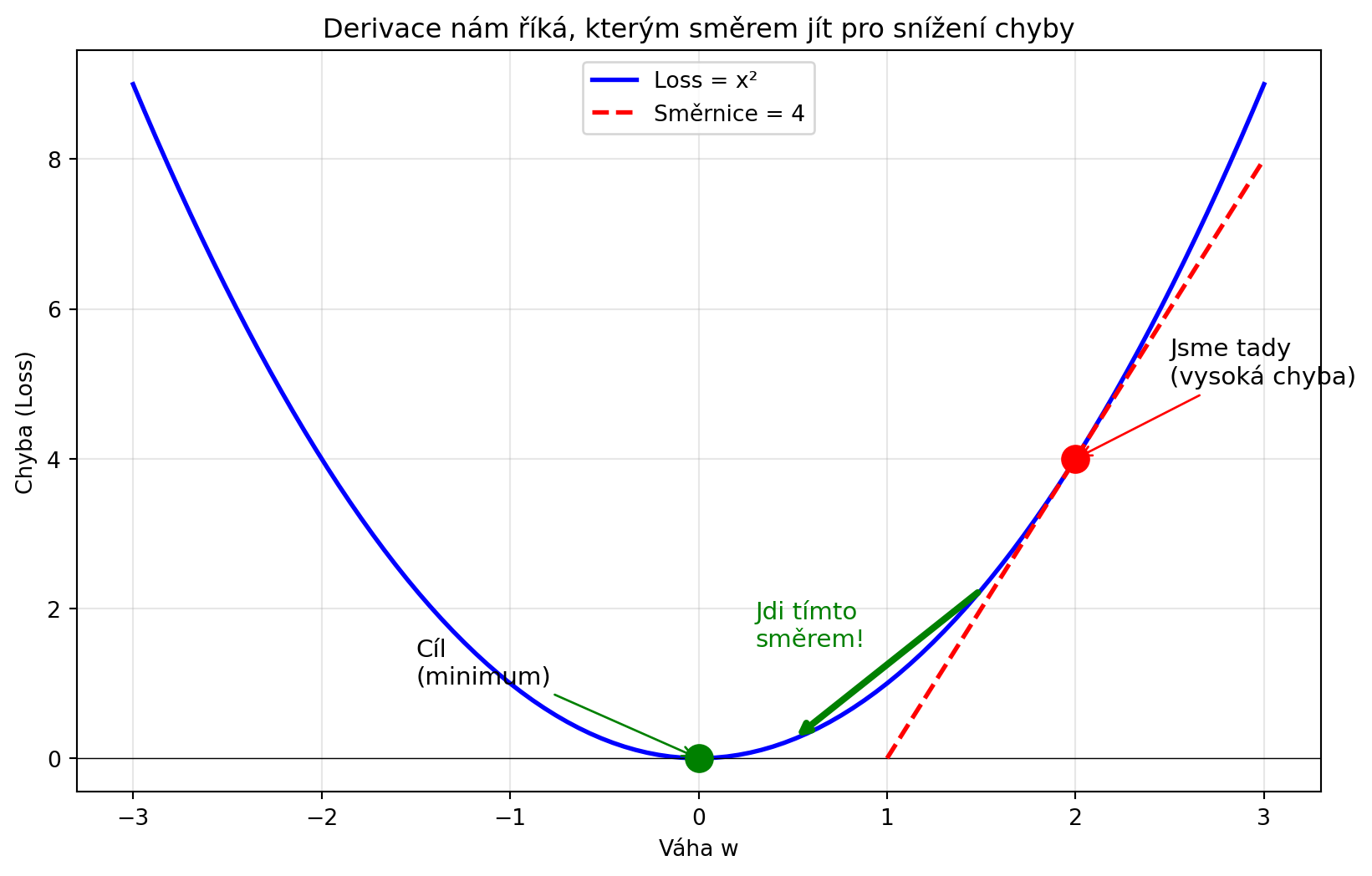
Derivace odpovídá na základní otázku: **Jak rychle se něco mění?**
V strojovém učení je to naprosto klíčové:
- Jak rychle se mění **chyba modelu** při změně vah?
- Kterým směrem změnit váhy, aby se chyba **zmenšila**?
- Jak "strmý" je loss landscape?
Bez derivací bychom neuměli trénovat neuronové sítě!
```{python}
#| fig-cap: "Derivace nám říká směr ke zlepšení"
#| code-fold: true
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
y = x**2 # Loss funkce
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(x, y, 'b-', linewidth=2, label='Loss = x²')
ax.axhline(y=0, color='k', linewidth=0.5)
# Bod a směr zlepšení
bod_x = 2
bod_y = bod_x**2
smernice = 2 * bod_x # Derivace v tomto bodě
ax.plot(bod_x, bod_y, 'ro', markersize=12)
ax.annotate('Jsme tady\n(vysoká chyba)', xy=(bod_x, bod_y),
xytext=(bod_x+0.5, bod_y+1), fontsize=11,
arrowprops=dict(arrowstyle='->', color='red'))
# Tečna
x_tecna = np.linspace(bod_x - 1, bod_x + 1, 50)
y_tecna = smernice * (x_tecna - bod_x) + bod_y
ax.plot(x_tecna, y_tecna, 'r--', linewidth=2, label=f'Směrnice = {smernice}')
# Šipka směrem dolů
ax.annotate('', xy=(0.5, 0.25), xytext=(1.5, 2.25),
arrowprops=dict(arrowstyle='->', color='green', lw=3))
ax.text(0.3, 1.5, 'Jdi tímto\nsměrem!', fontsize=11, color='green')
ax.plot(0, 0, 'go', markersize=12)
ax.annotate('Cíl\n(minimum)', xy=(0, 0), xytext=(-1.5, 1), fontsize=11,
arrowprops=dict(arrowstyle='->', color='green'))
ax.set_xlabel('Váha w')
ax.set_ylabel('Chyba (Loss)')
ax.set_title('Derivace nám říká, kterým směrem jít pro snížení chyby')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()
```
---
## Průměrná rychlost změny
Začneme jednodušším konceptem: **průměrná rychlost změny**.
Představte si, že jedete autem. Za 2 hodiny ujedete 120 km. Jaká byla průměrná rychlost?
$$\text{průměrná rychlost} = \frac{\text{změna vzdálenosti}}{\text{změna času}} = \frac{120 \text{ km}}{2 \text{ h}} = 60 \text{ km/h}$$
Obecně pro funkci $f(x)$:
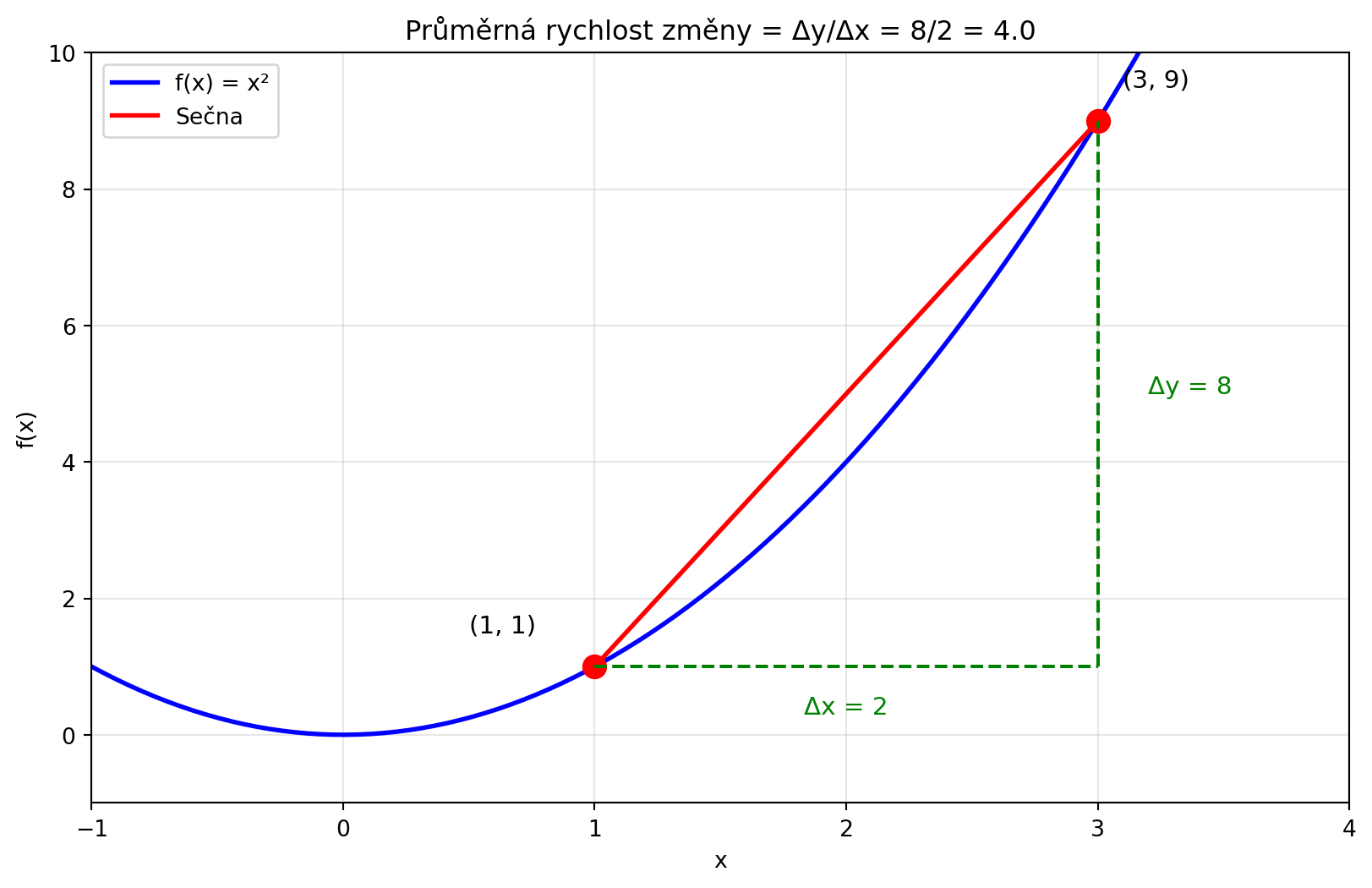
$$\text{průměrná rychlost změny} = \frac{f(x_2) - f(x_1)}{x_2 - x_1} = \frac{\Delta f}{\Delta x}$$
```{python}
#| fig-cap: "Průměrná rychlost změny = sklon sečny"
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**2
x = np.linspace(-1, 4, 100)
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(x, f(x), 'b-', linewidth=2, label='f(x) = x²')
# Dva body
x1, x2 = 1, 3
y1, y2 = f(x1), f(x2)
ax.plot([x1, x2], [y1, y2], 'ro', markersize=10)
ax.plot([x1, x2], [y1, y2], 'r-', linewidth=2, label='Sečna')
# Popisky
ax.annotate(f'({x1}, {y1})', xy=(x1, y1), xytext=(x1-0.5, y1+0.5), fontsize=11)
ax.annotate(f'({x2}, {y2})', xy=(x2, y2), xytext=(x2+0.1, y2+0.5), fontsize=11)
# Delta x a delta y
ax.plot([x1, x2], [y1, y1], 'g--', linewidth=1.5)
ax.plot([x2, x2], [y1, y2], 'g--', linewidth=1.5)
ax.text((x1+x2)/2, y1-0.7, f'Δx = {x2-x1}', fontsize=11, ha='center', color='green')
ax.text(x2+0.2, (y1+y2)/2, f'Δy = {y2-y1}', fontsize=11, color='green')
prumerna = (y2 - y1) / (x2 - x1)
ax.set_title(f'Průměrná rychlost změny = Δy/Δx = {y2-y1}/{x2-x1} = {prumerna}')
ax.set_xlabel('x')
ax.set_ylabel('f(x)')
ax.legend()
ax.grid(True, alpha=0.3)
ax.set_xlim(-1, 4)
ax.set_ylim(-1, 10)
plt.show()
```
```{python}
def prumerna_rychlost_zmeny(f, x1, x2):
"""Vypočítá průměrnou rychlost změny funkce f mezi x1 a x2."""
return (f(x2) - f(x1)) / (x2 - x1)
def f(x):
return x**2
# Průměrná rychlost změny mezi x=1 a x=3
rychlost = prumerna_rychlost_zmeny(f, 1, 3)
print(f"f(x) = x²")
print(f"Průměrná rychlost změny mezi x=1 a x=3: {rychlost}")
print(f"Δy = f(3) - f(1) = 9 - 1 = 8")
print(f"Δx = 3 - 1 = 2")
print(f"Průměrná rychlost = 8/2 = 4")
```
---
## Okamžitá rychlost změny (derivace)
Co když chceme vědět rychlost změny **v jednom konkrétním bodě**?
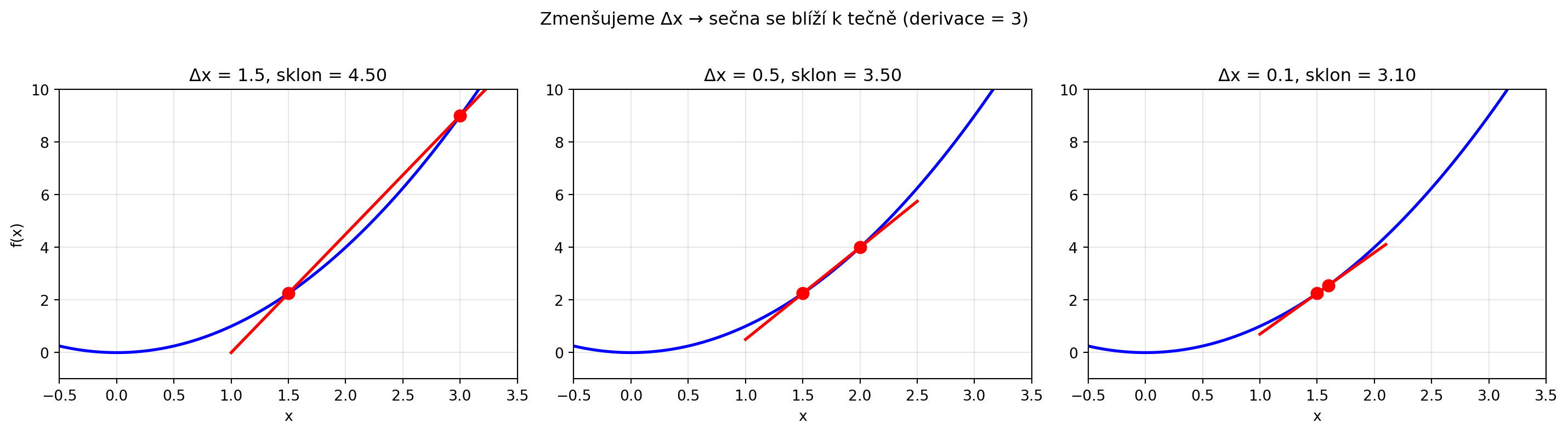
Musíme interval zmenšit na "nekonečně malý":
$$f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$$
Toto je **derivace** funkce $f$ v bodě $x$. Značíme ji $f'(x)$ nebo $\frac{df}{dx}$.
```{python}
#| fig-cap: "Od sečny k tečně"
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**2
x = np.linspace(-0.5, 3.5, 100)
bod = 1.5
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
delty = [1.5, 0.5, 0.1]
for ax, delta in zip(axes, delty):
ax.plot(x, f(x), 'b-', linewidth=2)
# Sečna
x1, x2 = bod, bod + delta
y1, y2 = f(x1), f(x2)
sklon = (y2 - y1) / (x2 - x1)
# Prodloužená sečna
x_secna = np.linspace(bod - 0.5, bod + delta + 0.5, 50)
y_secna = sklon * (x_secna - x1) + y1
ax.plot(x_secna, y_secna, 'r-', linewidth=2)
ax.plot([x1, x2], [y1, y2], 'ro', markersize=8)
ax.set_title(f'Δx = {delta}, sklon = {sklon:.2f}')
ax.set_xlim(-0.5, 3.5)
ax.set_ylim(-1, 10)
ax.grid(True, alpha=0.3)
ax.set_xlabel('x')
# Skutečná derivace v bodě 1.5 je 2*1.5 = 3
axes[0].set_ylabel('f(x)')
fig.suptitle('Zmenšujeme Δx → sečna se blíží k tečně (derivace = 3)', y=1.02)
plt.tight_layout()
plt.show()
```
### Numerická aproximace derivace
```{python}
def numericka_derivace(f, x, h=1e-5):
"""Aproximuje derivaci pomocí malého kroku h."""
return (f(x + h) - f(x)) / h
def f(x):
return x**2
# Derivace v bodě x=2
bod = 2
aprox = numericka_derivace(f, bod)
print(f"Funkce: f(x) = x²")
print(f"Analytická derivace: f'(x) = 2x")
print(f"V bodě x = {bod}:")
print(f" Numerická aproximace: {aprox:.6f}")
print(f" Přesná hodnota: {2 * bod}")
```
```{python}
# Jak se aproximace zlepšuje s menším h
print("\nKonvergence při zmenšování h:")
for h in [1, 0.1, 0.01, 0.001, 0.0001, 0.00001]:
aprox = numericka_derivace(f, 2, h)
chyba = abs(aprox - 4)
print(f"h = {h:8.5f}: f'(2) ≈ {aprox:.8f}, chyba = {chyba:.8f}")
```
---
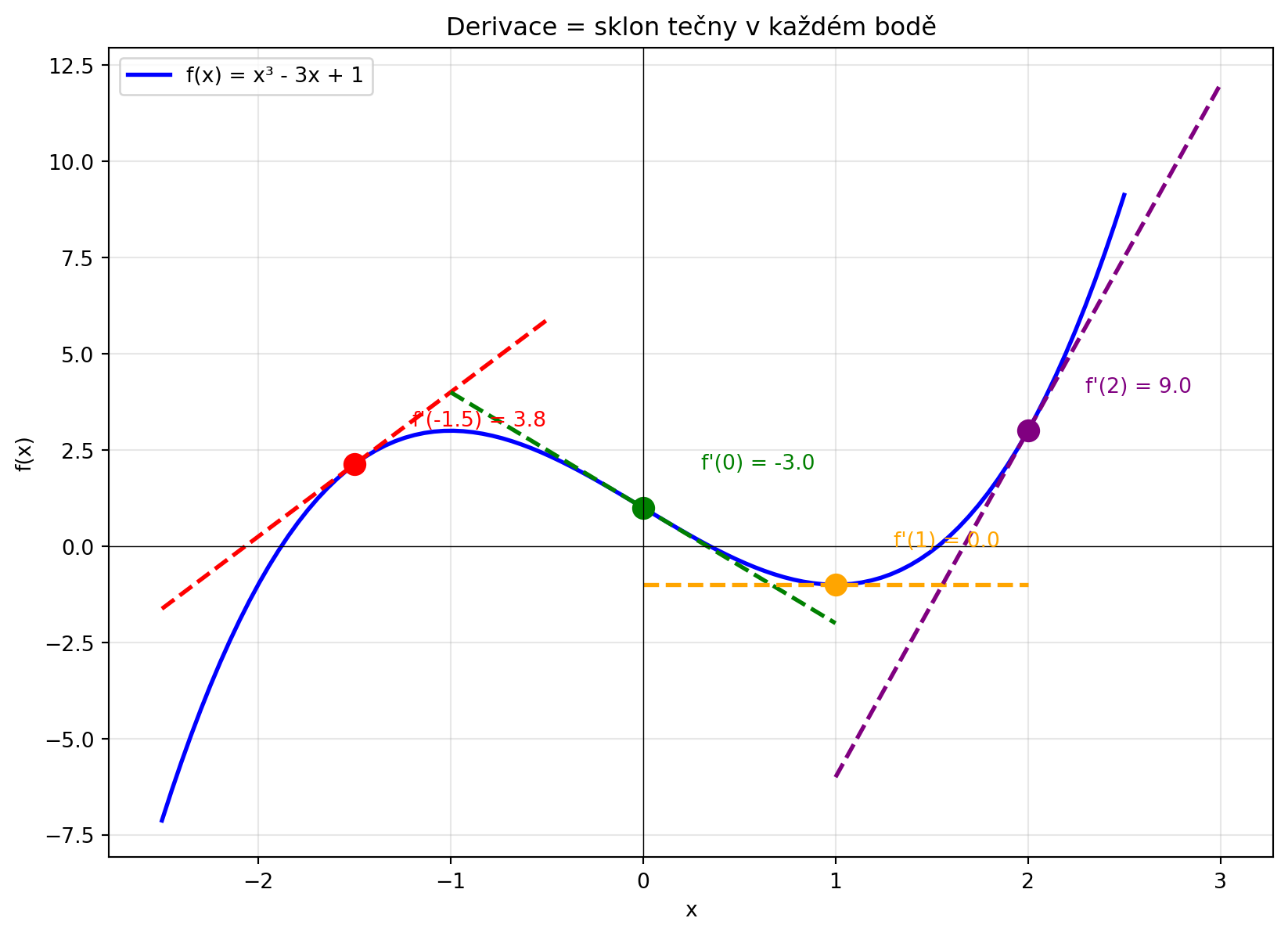
## Geometrická interpretace
Derivace $f'(x)$ je **sklon tečny** ke grafu funkce v bodě $x$.
```{python}
#| fig-cap: "Derivace = sklon tečny"
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**3 - 3*x + 1
def f_derivace(x):
return 3*x**2 - 3
x = np.linspace(-2.5, 2.5, 100)
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(x, f(x), 'b-', linewidth=2, label='f(x) = x³ - 3x + 1')
# Tečny v několika bodech
body = [-1.5, 0, 1, 2]
barvy = ['red', 'green', 'orange', 'purple']
for bod, barva in zip(body, barvy):
y_bod = f(bod)
sklon = f_derivace(bod)
# Tečna
x_tecna = np.linspace(bod - 1, bod + 1, 50)
y_tecna = sklon * (x_tecna - bod) + y_bod
ax.plot(x_tecna, y_tecna, color=barva, linewidth=2, linestyle='--')
ax.plot(bod, y_bod, 'o', color=barva, markersize=10)
ax.annotate(f"f'({bod}) = {sklon:.1f}", xy=(bod, y_bod),
xytext=(bod+0.3, y_bod+1), fontsize=10, color=barva)
ax.axhline(y=0, color='k', linewidth=0.5)
ax.axvline(x=0, color='k', linewidth=0.5)
ax.set_xlabel('x')
ax.set_ylabel('f(x)')
ax.set_title('Derivace = sklon tečny v každém bodě')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()
```
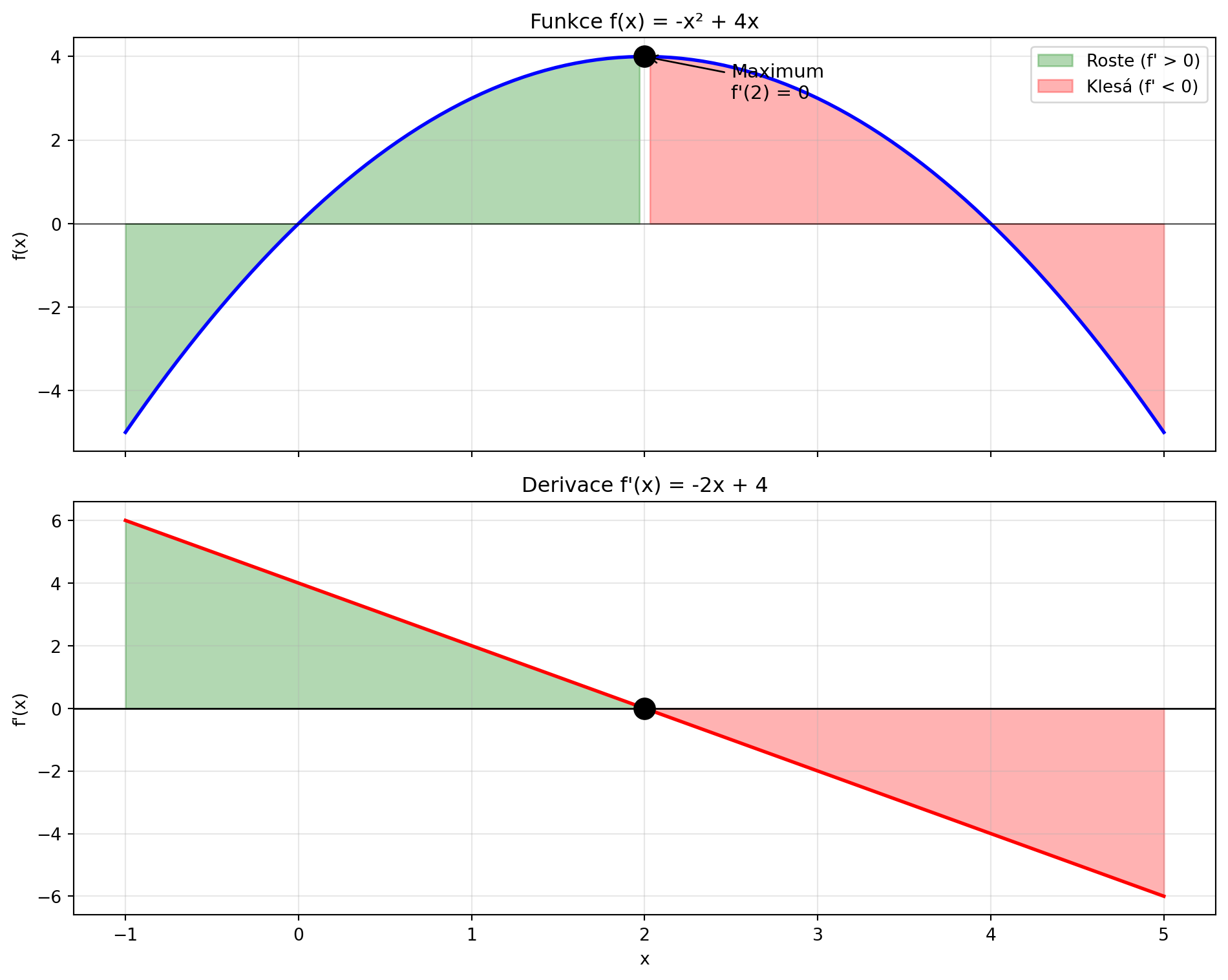
### Co nám derivace říká
| Derivace | Sklon | Funkce |
|----------|-------|--------|
| f'(x) > 0 | Kladný (/) | Roste |
| f'(x) = 0 | Nulový (—) | Lokální extrém |
| f'(x) < 0 | Záporný (\\) | Klesá |
```{python}
#| fig-cap: "Derivace a růst/pokles funkce"
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return -x**2 + 4*x
def f_derivace(x):
return -2*x + 4
x = np.linspace(-1, 5, 100)
fig, axes = plt.subplots(2, 1, figsize=(10, 8), sharex=True)
# Původní funkce
axes[0].plot(x, f(x), 'b-', linewidth=2)
axes[0].axhline(y=0, color='k', linewidth=0.5)
axes[0].fill_between(x[x < 2], f(x[x < 2]), alpha=0.3, color='green', label='Roste (f\' > 0)')
axes[0].fill_between(x[x > 2], f(x[x > 2]), alpha=0.3, color='red', label='Klesá (f\' < 0)')
axes[0].plot(2, f(2), 'ko', markersize=12)
axes[0].annotate('Maximum\nf\'(2) = 0', xy=(2, f(2)), xytext=(2.5, 3), fontsize=11,
arrowprops=dict(arrowstyle='->', color='black'))
axes[0].set_ylabel('f(x)')
axes[0].set_title('Funkce f(x) = -x² + 4x')
axes[0].legend()
axes[0].grid(True, alpha=0.3)
# Derivace
axes[1].plot(x, f_derivace(x), 'r-', linewidth=2)
axes[1].axhline(y=0, color='k', linewidth=1)
axes[1].fill_between(x[x < 2], f_derivace(x[x < 2]), 0, alpha=0.3, color='green')
axes[1].fill_between(x[x > 2], f_derivace(x[x > 2]), 0, alpha=0.3, color='red')
axes[1].plot(2, 0, 'ko', markersize=12)
axes[1].set_xlabel('x')
axes[1].set_ylabel("f'(x)")
axes[1].set_title("Derivace f'(x) = -2x + 4")
axes[1].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
---
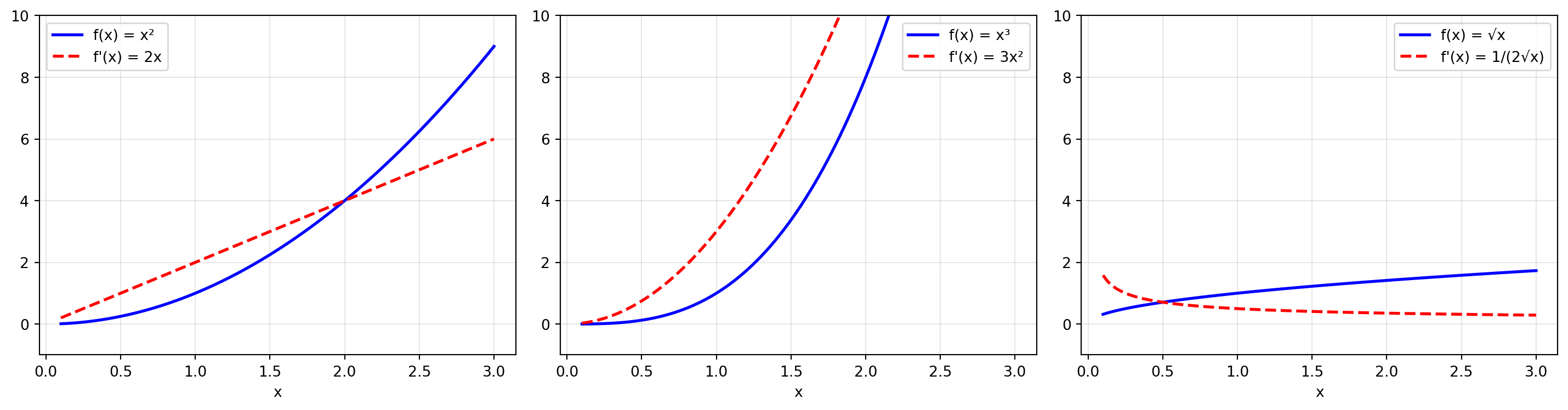
## Derivace základních funkcí
Některé derivace si zapamatujeme:
| Funkce $f(x)$ | Derivace $f'(x)$ |
|---------------|------------------|
| $c$ (konstanta) | $0$ |
| $x$ | $1$ |
| $x^n$ | $n \cdot x^{n-1}$ |
| $e^x$ | $e^x$ |
| $\ln(x)$ | $\frac{1}{x}$ |
| $\sin(x)$ | $\cos(x)$ |
| $\cos(x)$ | $-\sin(x)$ |
```{python}
#| fig-cap: "Derivace mocninných funkcí"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0.1, 3, 100)
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
funkce = [
(lambda x: x**2, lambda x: 2*x, 'x²', '2x'),
(lambda x: x**3, lambda x: 3*x**2, 'x³', '3x²'),
(lambda x: np.sqrt(x), lambda x: 1/(2*np.sqrt(x)), '√x', '1/(2√x)')
]
for ax, (f, df, nazev_f, nazev_df) in zip(axes, funkce):
ax.plot(x, f(x), 'b-', linewidth=2, label=f'f(x) = {nazev_f}')
ax.plot(x, df(x), 'r--', linewidth=2, label=f"f'(x) = {nazev_df}")
ax.set_xlabel('x')
ax.legend()
ax.grid(True, alpha=0.3)
ax.set_ylim(-1, 10)
plt.tight_layout()
plt.show()
```
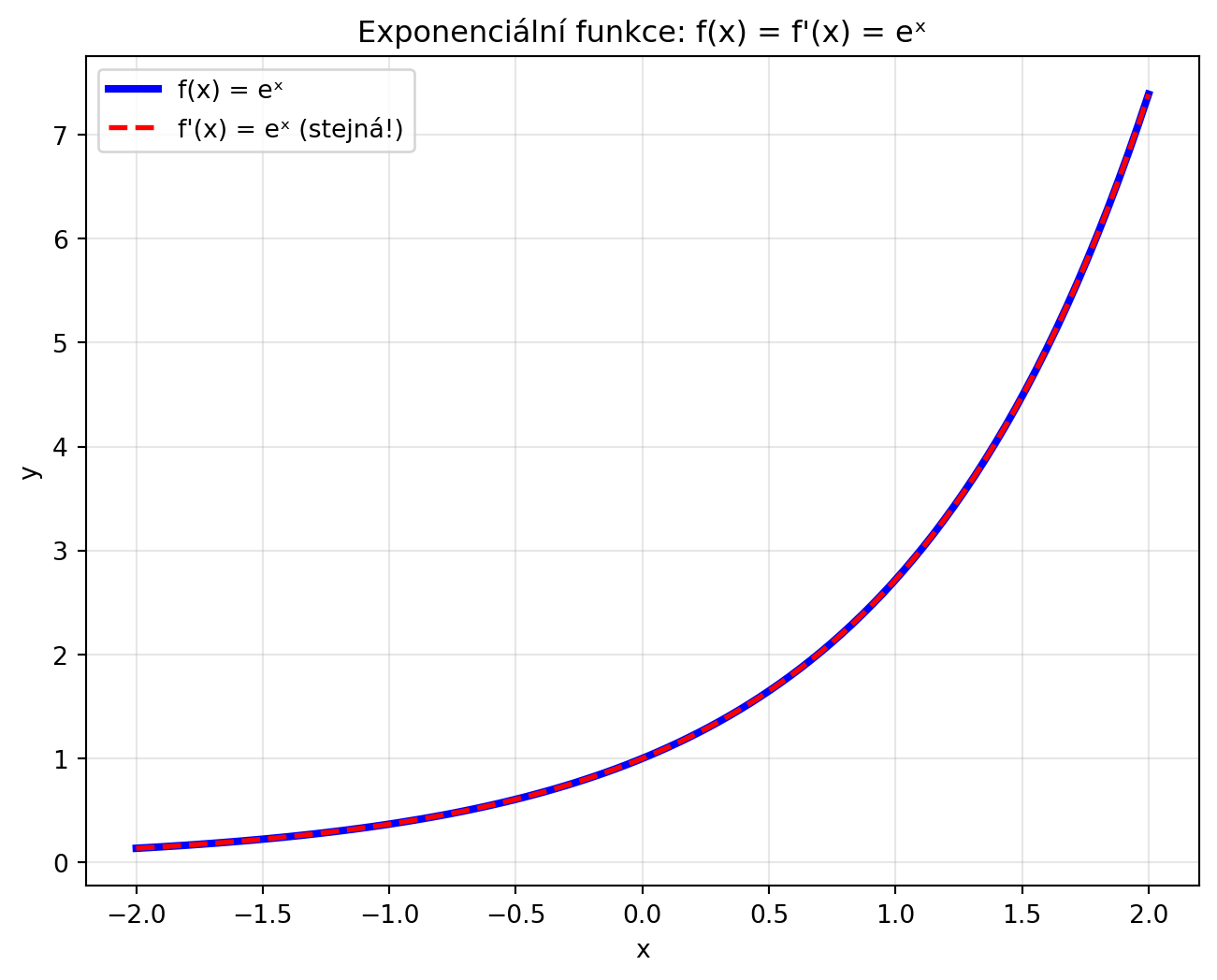
### Speciální případ: $e^x$
Funkce $e^x$ je unikátní -- její derivace je ona sama!
$$\frac{d}{dx} e^x = e^x$$
```{python}
#| fig-cap: "e^x je sama sobě derivací"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 2, 100)
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x, np.exp(x), 'b-', linewidth=3, label='f(x) = eˣ')
ax.plot(x, np.exp(x), 'r--', linewidth=2, label="f'(x) = eˣ (stejná!)")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Exponenciální funkce: f(x) = f\'(x) = eˣ')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()
print("V každém bodě: sklon tečny = hodnota funkce")
for x_val in [-1, 0, 1, 2]:
print(f"x = {x_val}: f({x_val}) = e^{x_val} = {np.exp(x_val):.4f} = f'({x_val})")
```
---
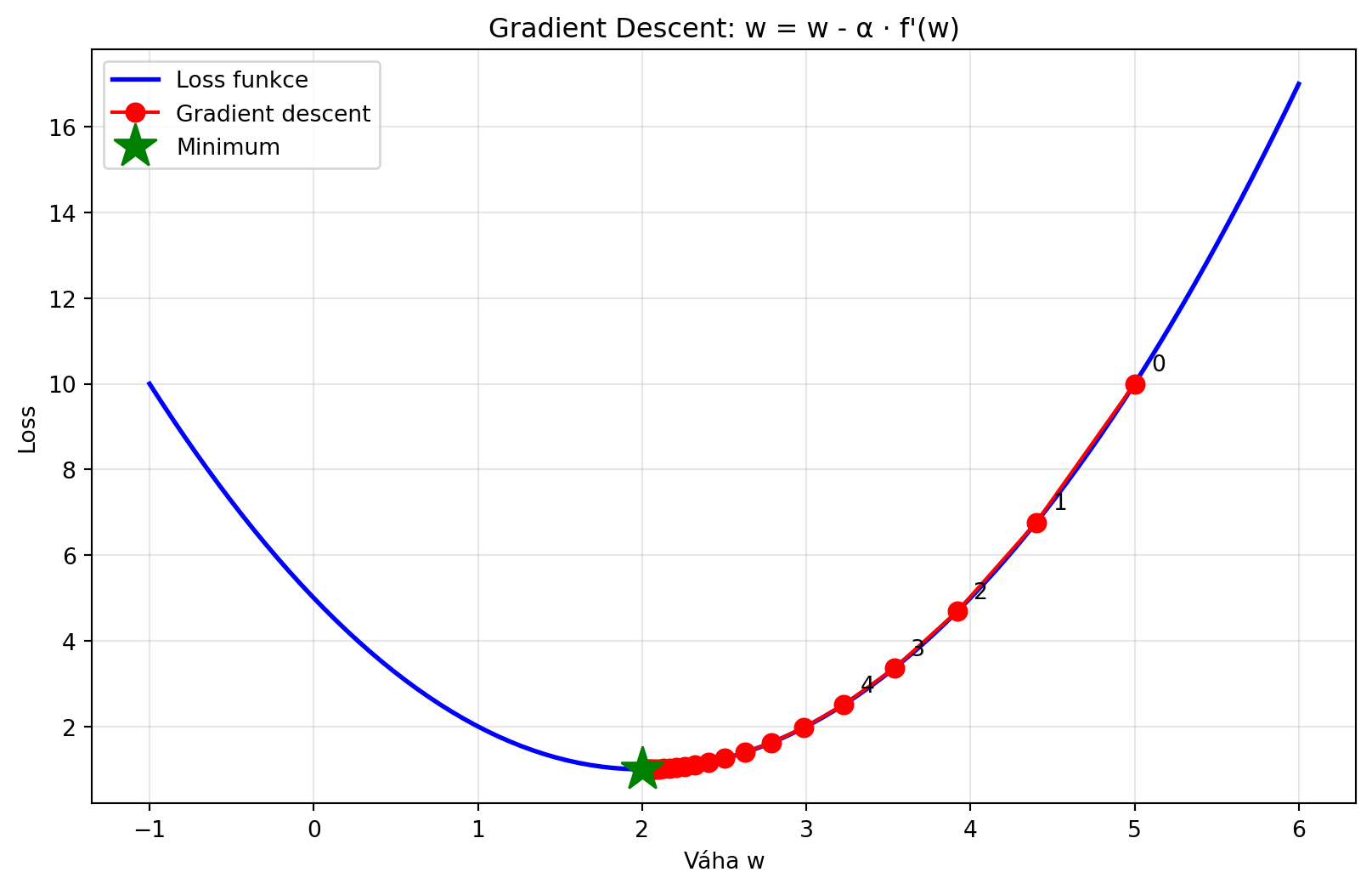
## Aplikace: Gradient Descent preview
V strojovém učení používáme derivaci k nalezení minima loss funkce:
```{python}
#| fig-cap: "Gradient descent - preview"
import numpy as np
import matplotlib.pyplot as plt
def loss(w):
return (w - 2)**2 + 1
def loss_derivace(w):
return 2 * (w - 2)
# Gradient descent
w = 5.0 # Počáteční bod
learning_rate = 0.1
historie = [w]
for i in range(20):
gradient = loss_derivace(w)
w = w - learning_rate * gradient # Klíčový krok!
historie.append(w)
# Vizualizace
x = np.linspace(-1, 6, 100)
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(x, loss(x), 'b-', linewidth=2, label='Loss funkce')
ax.plot(historie, [loss(w) for w in historie], 'ro-', markersize=8, label='Gradient descent')
ax.plot(2, 1, 'g*', markersize=20, label='Minimum')
for i, (w, l) in enumerate(zip(historie[:5], [loss(w) for w in historie[:5]])):
ax.annotate(f'{i}', xy=(w, l), xytext=(w+0.1, l+0.3), fontsize=10)
ax.set_xlabel('Váha w')
ax.set_ylabel('Loss')
ax.set_title('Gradient Descent: w = w - α · f\'(w)')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()
print(f"Počáteční w: {historie[0]}")
print(f"Konečné w: {historie[-1]:.4f}")
print(f"Optimální w: 2")
```
---
## Řešené příklady
### Příklad 1: Průměrná rychlost změny
Funkce $f(x) = x^2 - 2x$. Jaká je průměrná rychlost změny mezi $x = 1$ a $x = 4$?
```{python}
def f(x):
return x**2 - 2*x
x1, x2 = 1, 4
prz = (f(x2) - f(x1)) / (x2 - x1)
print(f"f(1) = 1 - 2 = {f(1)}")
print(f"f(4) = 16 - 8 = {f(4)}")
print(f"Průměrná rychlost = (8 - (-1)) / (4 - 1) = 9/3 = {prz}")
```
### Příklad 2: Derivace mocniny
Najděte derivaci $f(x) = x^5$.
**Řešení:** Použijeme pravidlo $(x^n)' = n \cdot x^{n-1}$
$$f'(x) = 5x^4$$
```{python}
def f(x):
return x**5
def f_derivace(x):
return 5 * x**4
# Ověření numericky
bod = 2
print(f"f(x) = x⁵, f'(x) = 5x⁴")
print(f"f'({bod}) = 5 · {bod}⁴ = {f_derivace(bod)}")
print(f"Numerická aproximace: {numericka_derivace(f, bod):.4f}")
```
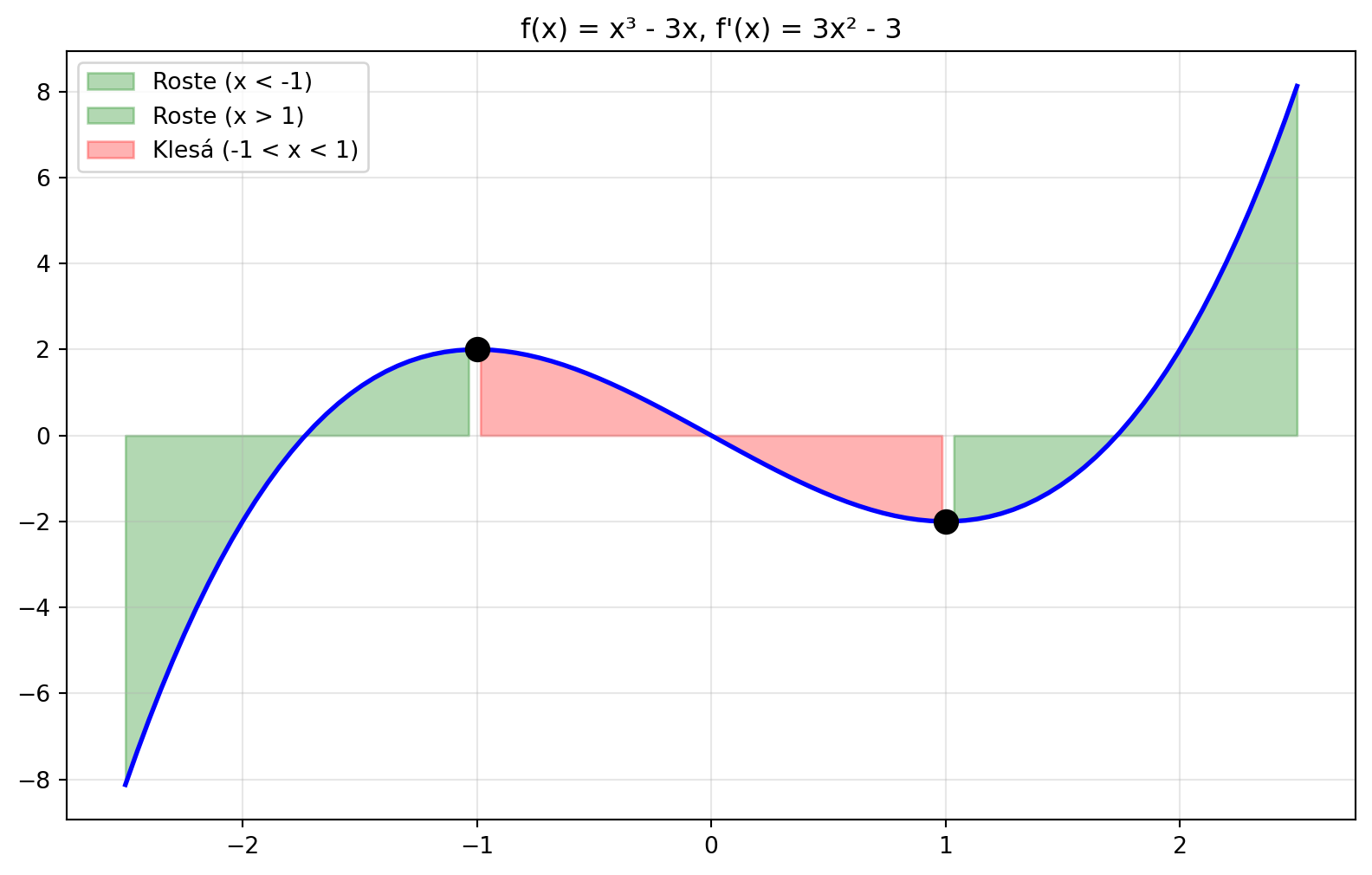
### Příklad 3: Kde je funkce rostoucí?
Pro $f(x) = x^3 - 3x$ určete, kde funkce roste.
```{python}
# f'(x) = 3x² - 3 = 3(x² - 1) = 3(x-1)(x+1)
# f'(x) > 0 když x < -1 nebo x > 1
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2.5, 2.5, 100)
def f(x):
return x**3 - 3*x
def f_der(x):
return 3*x**2 - 3
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(x, f(x), 'b-', linewidth=2)
# Rostoucí oblasti
ax.fill_between(x[x < -1], f(x[x < -1]), alpha=0.3, color='green', label='Roste (x < -1)')
ax.fill_between(x[x > 1], f(x[x > 1]), alpha=0.3, color='green', label='Roste (x > 1)')
ax.fill_between(x[(x >= -1) & (x <= 1)], f(x[(x >= -1) & (x <= 1)]),
alpha=0.3, color='red', label='Klesá (-1 < x < 1)')
ax.plot([-1, 1], [f(-1), f(1)], 'ko', markersize=10)
ax.set_title("f(x) = x³ - 3x, f'(x) = 3x² - 3")
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()
print("f'(x) = 3x² - 3 = 3(x² - 1)")
print("f'(x) = 0 pro x = ±1")
print("f'(x) > 0 (roste) pro x < -1 nebo x > 1")
print("f'(x) < 0 (klesá) pro -1 < x < 1")
```
### Příklad 4: Numerická derivace
Aproximujte derivaci $f(x) = \sin(x)$ v bodě $x = \pi/4$.
```{python}
import numpy as np
bod = np.pi / 4
# Numerická aproximace
h = 0.0001
aprox = (np.sin(bod + h) - np.sin(bod)) / h
# Přesná hodnota: derivace sin(x) je cos(x)
presna = np.cos(bod)
print(f"Bod: x = π/4 ≈ {bod:.4f}")
print(f"Numerická aproximace f'(π/4): {aprox:.6f}")
print(f"Přesná hodnota cos(π/4): {presna:.6f}")
print(f"Chyba: {abs(aprox - presna):.8f}")
```
---
## Cvičení
::: {.callout-warning title="Cvičení 1: Průměrná rychlost"}
Vypočítejte průměrnou rychlost změny funkce $f(x) = 2x + 3$ mezi $x = 1$ a $x = 5$.
**Výsledek:** 2
<details>
<summary>Řešení</summary>
$\frac{f(5) - f(1)}{5 - 1} = \frac{13 - 5}{4} = \frac{8}{4} = 2$
(Pro lineární funkci je průměrná rychlost rovna směrnici.)
</details>
:::
::: {.callout-warning title="Cvičení 2: Derivace mocniny"}
Najděte derivaci $f(x) = x^4$.
**Výsledek:** $f'(x) = 4x^3$
:::
::: {.callout-warning title="Cvičení 3: Derivace v bodě"}
Pro $f(x) = x^2 + 3x$ vypočítejte $f'(2)$.
**Výsledek:** 7
<details>
<summary>Řešení</summary>
$f'(x) = 2x + 3$
$f'(2) = 2 \cdot 2 + 3 = 7$
</details>
:::
::: {.callout-warning title="Cvičení 4: Kde je extrém?"}
Najděte bod, kde má funkce $f(x) = x^2 - 6x + 5$ minimum.
**Výsledek:** $x = 3$
<details>
<summary>Řešení</summary>
$f'(x) = 2x - 6 = 0$
$x = 3$
</details>
:::
::: {.callout-warning title="Cvičení 5: Numerická derivace"}
Napište funkci, která numericky aproximuje derivaci v bodě pomocí centrální diference:
$$f'(x) \approx \frac{f(x+h) - f(x-h)}{2h}$$
<details>
<summary>Řešení</summary>
```python
def centralni_derivace(f, x, h=1e-5):
return (f(x + h) - f(x - h)) / (2 * h)
```
</details>
:::
::: {.callout-warning title="Cvičení 6: Interpretace"}
Pokud $f'(3) = -2$, co to říká o funkci v bodě $x = 3$?
**Odpověď:** Funkce v bodě $x = 3$ klesá, sklon tečny je -2.
:::
---
## Shrnutí
::: {.callout-note title="Co si zapamatovat"}
- **Průměrná rychlost změny** = $\frac{\Delta f}{\Delta x}$ = sklon sečny
- **Derivace** = okamžitá rychlost změny = sklon tečny
- $f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$
- $f'(x) > 0$: funkce roste
- $f'(x) < 0$: funkce klesá
- $f'(x) = 0$: lokální extrém
- Klíčové derivace: $(x^n)' = nx^{n-1}$, $(e^x)' = e^x$
- V ML: derivace ukazuje směr ke snížení chyby
:::
V další kapitole se naučíme **pravidla derivování**, která nám umožní derivovat složitější funkce.