# Násobení matic
::: {.callout-tip title="Co se naučíte"}
V této kapitole se naučíte:
- Jak násobit matici vektorem
- Jak násobit dvě matice
- Proč násobení matic funguje tak, jak funguje
- Použití maticového násobení v neuronových sítích
:::
## Proč je násobení matic důležité?
Maticové násobení je **srdce** neuronových sítí. Každá vrstva neuronové sítě provádí:
$$\mathbf{y} = \mathbf{W}\mathbf{x} + \mathbf{b}$$
kde:
- $\mathbf{x}$ je vstupní vektor
- $\mathbf{W}$ je matice vah
- $\mathbf{b}$ je bias vektor
- $\mathbf{y}$ je výstupní vektor
Pochopení maticového násobení je tedy klíčové pro pochopení toho, jak AI funguje!
---
## Násobení matice vektorem
Začneme jednodušším případem: násobení matice $\mathbf{A}$ vektorem $\mathbf{x}$.
$$\mathbf{A}\mathbf{x} = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} a_{11}x_1 + a_{12}x_2 \\ a_{21}x_1 + a_{22}x_2 \end{bmatrix}$$
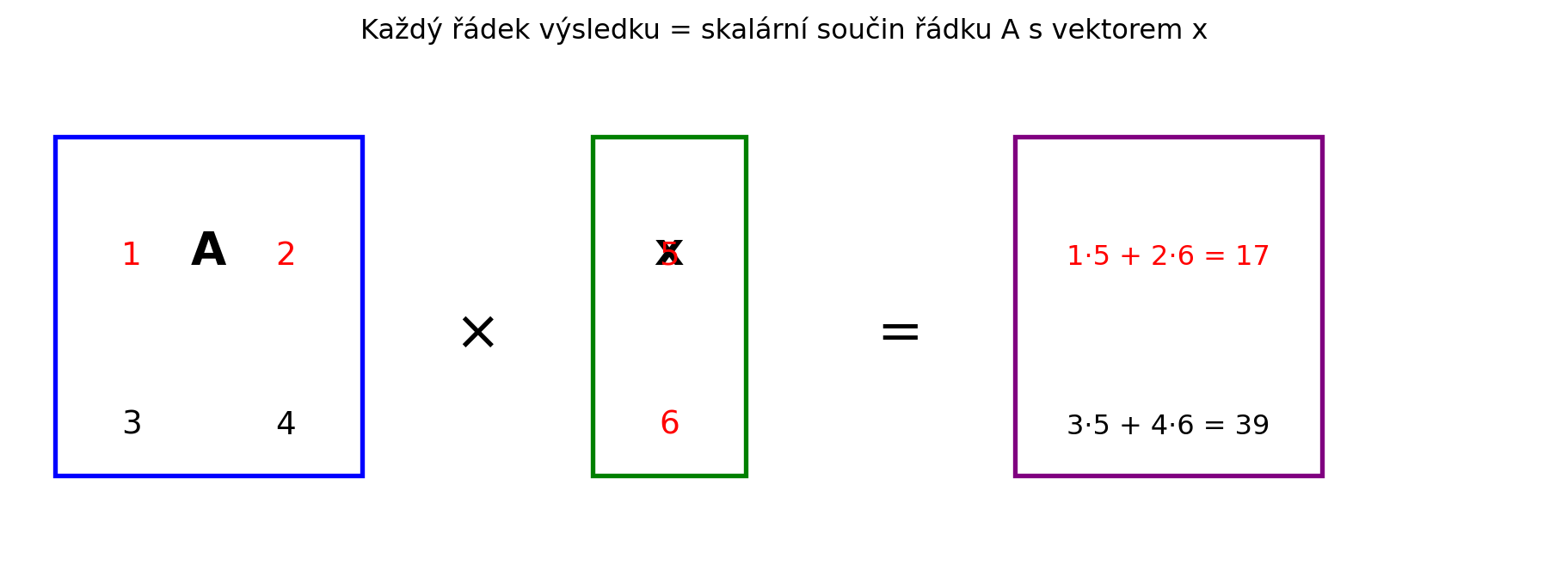
Každý prvek výsledku je **skalární součin** řádku matice s vektorem.
```{python}
import numpy as np
import matplotlib.pyplot as plt
A = np.array([
[1, 2],
[3, 4]
])
x = np.array([5, 6])
# Násobení
y = A @ x # nebo np.dot(A, x)
print("Matice A:")
print(A)
print(f"\nVektor x: {x}")
print(f"\nA @ x = [{1*5 + 2*6}, {3*5 + 4*6}] = {y}")
```
### Vizuální vysvětlení
```{python}
#| fig-cap: "Násobení matice vektorem"
#| code-fold: true
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12, 4))
# Matice
ax.text(0.5, 0.7, r'$\mathbf{A}$', fontsize=20, ha='center')
ax.add_patch(plt.Rectangle((0.1, 0.2), 0.8, 0.8, fill=False, edgecolor='blue', lw=2))
ax.text(0.3, 0.7, '1', fontsize=14, ha='center', color='red')
ax.text(0.7, 0.7, '2', fontsize=14, ha='center', color='red')
ax.text(0.3, 0.3, '3', fontsize=14, ha='center')
ax.text(0.7, 0.3, '4', fontsize=14, ha='center')
# Krát
ax.text(1.2, 0.5, '×', fontsize=24, ha='center')
# Vektor
ax.text(1.7, 0.7, r'$\mathbf{x}$', fontsize=20, ha='center')
ax.add_patch(plt.Rectangle((1.5, 0.2), 0.4, 0.8, fill=False, edgecolor='green', lw=2))
ax.text(1.7, 0.7, '5', fontsize=14, ha='center', color='red')
ax.text(1.7, 0.3, '6', fontsize=14, ha='center', color='red')
# Rovná se
ax.text(2.3, 0.5, '=', fontsize=24, ha='center')
# Výsledek
ax.add_patch(plt.Rectangle((2.6, 0.2), 0.8, 0.8, fill=False, edgecolor='purple', lw=2))
ax.text(3.0, 0.7, '1·5 + 2·6 = 17', fontsize=12, ha='center', color='red')
ax.text(3.0, 0.3, '3·5 + 4·6 = 39', fontsize=12, ha='center')
ax.set_xlim(0, 4)
ax.set_ylim(0, 1.2)
ax.axis('off')
ax.set_title('Každý řádek výsledku = skalární součin řádku A s vektorem x', fontsize=12)
plt.show()
```
### Pravidlo rozměrů
Pro násobení $\mathbf{A} \cdot \mathbf{x}$:
- $\mathbf{A}$ má rozměr $m \times n$
- $\mathbf{x}$ má rozměr $n$ (nebo $n \times 1$)
- Výsledek má rozměr $m$ (nebo $m \times 1$)
::: {.callout-warning title="Důležité!"}
Počet **sloupců matice** musí být roven **délce vektoru**!
:::
```{python}
import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6]]) # 2×3
x = np.array([1, 2, 3]) # 3 prvky
y = A @ x
print(f"A: {A.shape}")
print(f"x: {x.shape}")
print(f"y = A @ x: {y.shape}")
print(f"y = {y}")
```
---
## Násobení dvou matic
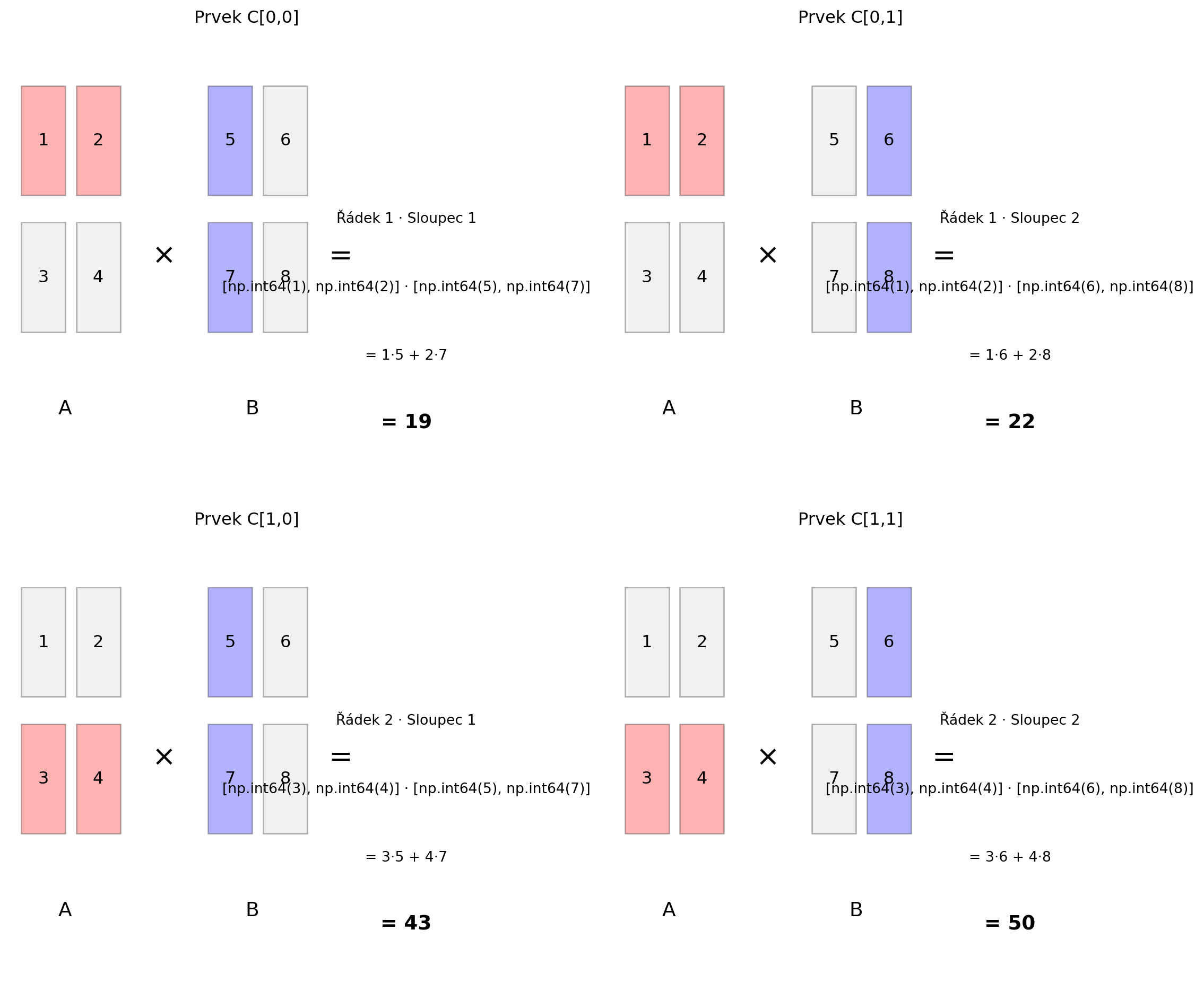
Při násobení matic $\mathbf{C} = \mathbf{A} \cdot \mathbf{B}$ je prvek $c_{ij}$ skalární součin **i-tého řádku A** a **j-tého sloupce B**.
$$c_{ij} = \sum_{k=1}^{n} a_{ik} \cdot b_{kj}$$
```{python}
import numpy as np
A = np.array([
[1, 2],
[3, 4]
])
B = np.array([
[5, 6],
[7, 8]
])
C = A @ B
print("A =")
print(A)
print("\nB =")
print(B)
print("\nA @ B =")
print(C)
# Ověření prvků
print(f"\nc[0,0] = 1·5 + 2·7 = {1*5 + 2*7}")
print(f"c[0,1] = 1·6 + 2·8 = {1*6 + 2*8}")
print(f"c[1,0] = 3·5 + 4·7 = {3*5 + 4*7}")
print(f"c[1,1] = 3·6 + 4·8 = {3*6 + 4*8}")
```
```{python}
#| fig-cap: "Násobení matic krok za krokem"
#| code-fold: true
import numpy as np
import matplotlib.pyplot as plt
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
pozice = [(0, 0), (0, 1), (1, 0), (1, 1)]
vysledky = [19, 22, 43, 50]
for idx, (ax, (i, j), vysl) in enumerate(zip(axes.flat, pozice, vysledky)):
# Matice A
for r in range(2):
for c in range(2):
color = 'red' if r == i else 'lightgray'
ax.add_patch(plt.Rectangle((c*0.5, 1-r*0.5), 0.4, 0.4,
facecolor=color, alpha=0.3, edgecolor='black'))
ax.text(c*0.5+0.2, 1.2-r*0.5, str(A[r, c]), ha='center', va='center', fontsize=12)
ax.text(0.4, 0.2, 'A', fontsize=14, ha='center')
# Krát
ax.text(1.3, 0.75, '×', fontsize=20, ha='center')
# Matice B
for r in range(2):
for c in range(2):
color = 'blue' if c == j else 'lightgray'
ax.add_patch(plt.Rectangle((1.7+c*0.5, 1-r*0.5), 0.4, 0.4,
facecolor=color, alpha=0.3, edgecolor='black'))
ax.text(1.7+c*0.5+0.2, 1.2-r*0.5, str(B[r, c]), ha='center', va='center', fontsize=12)
ax.text(2.1, 0.2, 'B', fontsize=14, ha='center')
# Rovná se
ax.text(2.9, 0.75, '=', fontsize=20, ha='center')
# Výpočet
radek_A = A[i, :]
sloupec_B = B[:, j]
ax.text(3.5, 0.9, f'Řádek {i+1} · Sloupec {j+1}', fontsize=10, ha='center')
ax.text(3.5, 0.65, f'{list(radek_A)} · {list(sloupec_B)}', fontsize=10, ha='center')
ax.text(3.5, 0.4, f'= {radek_A[0]}·{sloupec_B[0]} + {radek_A[1]}·{sloupec_B[1]}',
fontsize=10, ha='center')
ax.text(3.5, 0.15, f'= {vysl}', fontsize=14, ha='center', fontweight='bold')
ax.set_xlim(-0.1, 4.2)
ax.set_ylim(-0.1, 1.6)
ax.axis('off')
ax.set_title(f'Prvek C[{i},{j}]', fontsize=12)
plt.tight_layout()
plt.show()
```
### Pravidlo rozměrů pro násobení matic
Pro násobení $\mathbf{A} \cdot \mathbf{B}$:
- $\mathbf{A}$ má rozměr $m \times n$
- $\mathbf{B}$ má rozměr $n \times p$
- Výsledek $\mathbf{C}$ má rozměr $m \times p$
::: {.callout-warning title="Vnitřní rozměry musí souhlasit!"}
Počet **sloupců A** = Počet **řádků B**
$(m \times \mathbf{n}) \cdot (\mathbf{n} \times p) = (m \times p)$
:::
```{python}
import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6]]) # 2×3
B = np.array([[1, 2], [3, 4], [5, 6]]) # 3×2
C = A @ B
print(f"A: {A.shape}")
print(f"B: {B.shape}")
print(f"C = A @ B: {C.shape}")
print("\nC =")
print(C)
```
---
## Důležité vlastnosti
### Násobení NENÍ komutativní!
$$\mathbf{A} \cdot \mathbf{B} \neq \mathbf{B} \cdot \mathbf{A}$$
```{python}
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
print("A @ B =")
print(A @ B)
print("\nB @ A =")
print(B @ A)
print(f"\nJsou stejné? {np.array_equal(A @ B, B @ A)}")
```
### Násobení jednotkovou maticí
$$\mathbf{A} \cdot \mathbf{I} = \mathbf{I} \cdot \mathbf{A} = \mathbf{A}$$
```{python}
import numpy as np
A = np.array([[1, 2], [3, 4]])
I = np.eye(2)
print("A @ I = A:")
print(A @ I)
print("\nI @ A = A:")
print(I @ A)
```
### Asociativita
$$(\mathbf{A} \cdot \mathbf{B}) \cdot \mathbf{C} = \mathbf{A} \cdot (\mathbf{B} \cdot \mathbf{C})$$
```{python}
import numpy as np
A = np.random.randn(2, 3)
B = np.random.randn(3, 4)
C = np.random.randn(4, 2)
leva = (A @ B) @ C
prava = A @ (B @ C)
print(f"(A @ B) @ C = A @ (B @ C): {np.allclose(leva, prava)}")
```
---
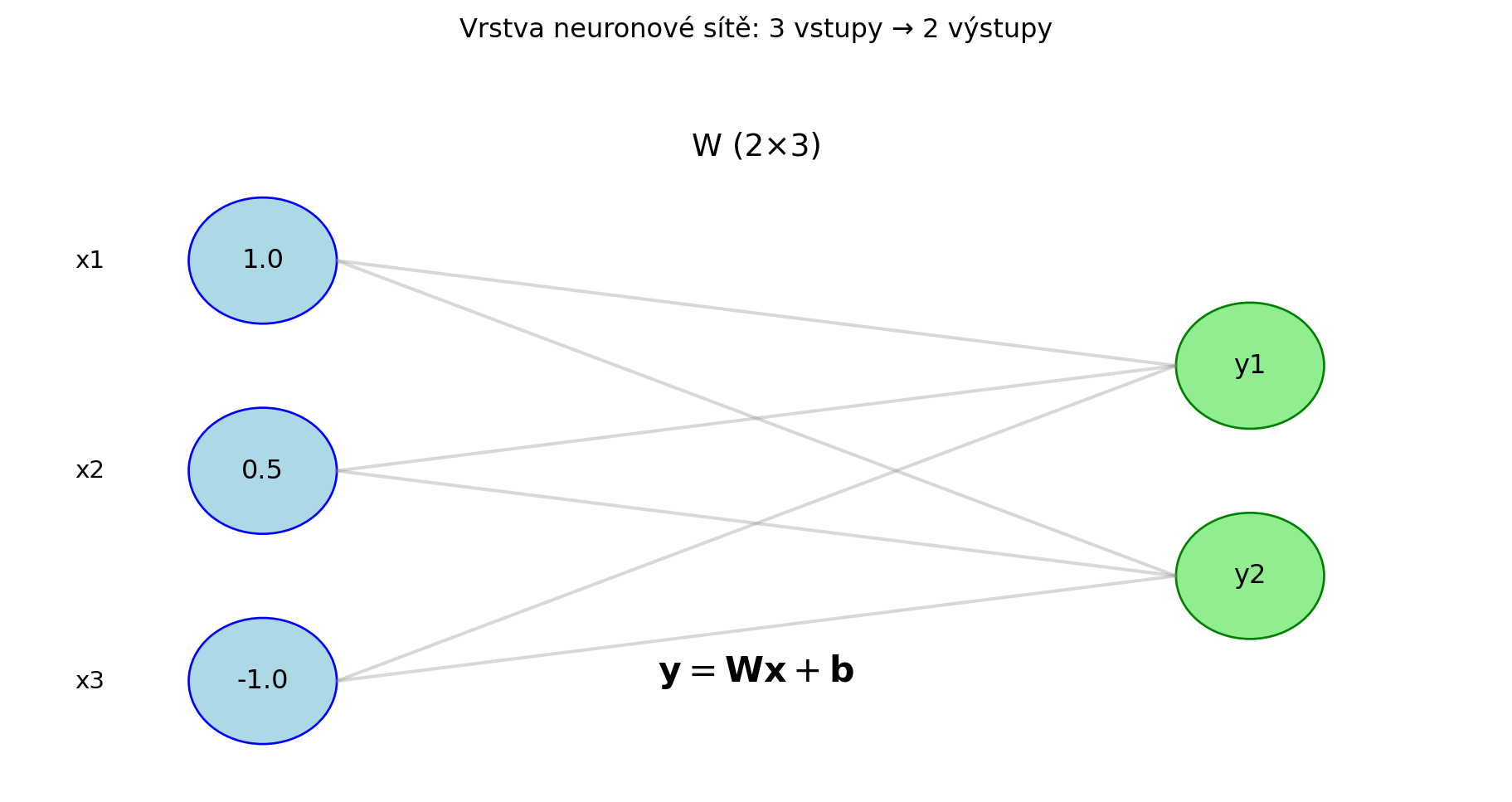
## Aplikace: Vrstva neuronové sítě
Jednoduchá vrstva neuronové sítě transformuje vstup takto:
$$\mathbf{y} = \mathbf{W}\mathbf{x} + \mathbf{b}$$
```{python}
# Vrstva s 3 vstupy a 2 výstupy
import numpy as np
np.random.seed(42)
# Vstup (3 neurony)
x = np.array([1.0, 0.5, -1.0])
# Váhy (matice 2×3)
W = np.random.randn(2, 3)
# Bias (vektor délky 2)
b = np.array([0.1, -0.1])
# Forward pass
y = W @ x + b
print(f"Vstup x: {x}")
print(f"\nVáhy W:\n{W.round(3)}")
print(f"\nBias b: {b}")
print(f"\nVýstup y = Wx + b: {y.round(3)}")
```
```{python}
#| fig-cap: "Vrstva neuronové sítě jako maticové násobení"
#| code-fold: true
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(12, 6))
# Vstupní neurony
for i, val in enumerate([1.0, 0.5, -1.0]):
y_pos = 2 - i
ax.add_patch(plt.Circle((1, y_pos), 0.3, facecolor='lightblue', edgecolor='blue'))
ax.text(1, y_pos, f'{val}', ha='center', va='center', fontsize=12)
ax.text(0.3, y_pos, f'x{i+1}', ha='center', va='center', fontsize=11)
# Výstupní neurony
for i in range(2):
y_pos = 1.5 - i
ax.add_patch(plt.Circle((5, y_pos), 0.3, facecolor='lightgreen', edgecolor='green'))
ax.text(5, y_pos, f'y{i+1}', ha='center', va='center', fontsize=12)
# Spojení (váhy)
for i in range(3):
for j in range(2):
ax.plot([1.3, 4.7], [2-i, 1.5-j], 'gray', alpha=0.3)
ax.text(3, 2.5, 'W (2×3)', ha='center', fontsize=14)
ax.text(3, 0, r'$\mathbf{y} = \mathbf{W}\mathbf{x} + \mathbf{b}$', ha='center', fontsize=16)
ax.set_xlim(0, 6)
ax.set_ylim(-0.5, 3)
ax.axis('off')
ax.set_title('Vrstva neuronové sítě: 3 vstupy → 2 výstupy')
plt.show()
```
### Batch zpracování
V praxi zpracováváme více vstupů najednou (batch). Vstupy poskládáme do matice:
```{python}
# 4 vstupy najednou (batch size = 4)
import numpy as np
X = np.array([
[1.0, 0.5, -1.0], # vzorek 1
[0.5, 1.0, 0.0], # vzorek 2
[-0.5, 0.5, 1.0], # vzorek 3
[1.0, 1.0, 1.0] # vzorek 4
])
print(f"Batch vstupů X: {X.shape}") # 4×3
# Pro batch násobíme zprava: Y = X @ W^T + b
# (protože chceme zachovat batch dimenzi)
Y = X @ W.T + b
print(f"Batch výstupů Y: {Y.shape}") # 4×2
print("\nVýstupy pro každý vzorek:")
print(Y.round(3))
```
---
## Řešené příklady
### Příklad 1: Matice krát vektor
Vypočítejte $\mathbf{A}\mathbf{x}$:
$$\mathbf{A} = \begin{bmatrix} 2 & 1 \\ 0 & 3 \end{bmatrix}, \quad \mathbf{x} = \begin{bmatrix} 4 \\ 5 \end{bmatrix}$$
```{python}
import numpy as np
A = np.array([[2, 1], [0, 3]])
x = np.array([4, 5])
y = A @ x
print(f"y[0] = 2·4 + 1·5 = {2*4 + 1*5}")
print(f"y[1] = 0·4 + 3·5 = {0*4 + 3*5}")
print(f"\nA @ x = {y}")
```
### Příklad 2: Násobení matic 2×2
Vypočítejte $\mathbf{A} \cdot \mathbf{B}$:
$$\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad \mathbf{B} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}$$
```{python}
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[0, 1], [1, 0]])
C = A @ B
print("Ruční výpočet:")
print(f"c[0,0] = 1·0 + 2·1 = {1*0 + 2*1}")
print(f"c[0,1] = 1·1 + 2·0 = {1*1 + 2*0}")
print(f"c[1,0] = 3·0 + 4·1 = {3*0 + 4*1}")
print(f"c[1,1] = 3·1 + 4·0 = {3*1 + 4*0}")
print(f"\nA @ B =\n{C}")
```
### Příklad 3: Kontrola rozměrů
Které násobení je možné?
- A (2×3) × B (3×4) → ?
- A (2×3) × B (2×4) → ?
- A (4×2) × B (2×1) → ?
```{python}
# A (2×3) × B (3×4) → (2×4) ✓
import numpy as np
A1 = np.random.randn(2, 3)
B1 = np.random.randn(3, 4)
print(f"(2×3) × (3×4) → {(A1 @ B1).shape} ✓")
# A (2×3) × B (2×4) → NELZE (3 ≠ 2)
print("(2×3) × (2×4) → NELZE (vnitřní rozměry nesouhlasí)")
# A (4×2) × B (2×1) → (4×1) ✓
A3 = np.random.randn(4, 2)
B3 = np.random.randn(2, 1)
print(f"(4×2) × (2×1) → {(A3 @ B3).shape} ✓")
```
### Příklad 4: Dvě vrstvy sítě
Máme síť se dvěma vrstvami:
- Vstup: 4 neurony
- Skrytá vrstva: 3 neurony
- Výstup: 2 neurony
```{python}
import numpy as np
np.random.seed(123)
# Vstup
x = np.array([1, 2, 3, 4])
# Váhy první vrstvy (3×4)
W1 = np.random.randn(3, 4)
# Váhy druhé vrstvy (2×3)
W2 = np.random.randn(2, 3)
# Forward pass
h = W1 @ x # skrytá vrstva (3 neurony)
y = W2 @ h # výstup (2 neurony)
print(f"Vstup x: {x.shape} → {x}")
print(f"Skrytá vrstva h: {h.shape} → {h.round(3)}")
print(f"Výstup y: {y.shape} → {y.round(3)}")
```
### Příklad 5: Transpozice a násobení
Ověřte, že $(\mathbf{A}\mathbf{B})^T = \mathbf{B}^T \mathbf{A}^T$:
```{python}
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
leva = (A @ B).T
prava = B.T @ A.T
print("(AB)^T =")
print(leva)
print("\nB^T @ A^T =")
print(prava)
print(f"\nJsou stejné: {np.array_equal(leva, prava)}")
```
---
## Cvičení
::: {.callout-warning title="Cvičení 1: Matice × vektor"}
Vypočítejte:
$$\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 5 \\ 3 \end{bmatrix}$$
**Výsledek:** [5, 3]
:::
::: {.callout-warning title="Cvičení 2: Násobení matic"}
Vypočítejte:
$$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$
**Výsledek:** $\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$
:::
::: {.callout-warning title="Cvičení 3: Rozměr výsledku"}
Jaký rozměr bude mít výsledek násobení matice 5×3 a matice 3×7?
**Výsledek:** 5×7
:::
::: {.callout-warning title="Cvičení 4: Je násobení možné?"}
Je možné vynásobit matici 2×3 maticí 4×2?
**Výsledek:** Ne (3 ≠ 4)
:::
::: {.callout-warning title="Cvičení 5: Vrstva sítě"}
Navrhněte rozměry váhové matice W pro vrstvu, která má 10 vstupů a 5 výstupů.
**Výsledek:** W má rozměr 5×10
<details>
<summary>Řešení</summary>
$\mathbf{y} = \mathbf{W}\mathbf{x}$
- x má rozměr 10
- y má rozměr 5
- W musí mít rozměr 5×10
</details>
:::
::: {.callout-warning title="Cvičení 6: Ruční výpočet"}
Vypočítejte ručně:
$$\begin{bmatrix} 2 & -1 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \end{bmatrix}$$
**Výsledek:** [0, 7]
<details>
<summary>Řešení</summary>
$y_1 = 2 \cdot 1 + (-1) \cdot 2 = 2 - 2 = 0$
$y_2 = 1 \cdot 1 + 3 \cdot 2 = 1 + 6 = 7$
</details>
:::
---
## Shrnutí
::: {.callout-note title="Co si zapamatovat"}
- **Matice × vektor**: každý prvek výsledku = skalární součin řádku s vektorem
- **Matice × matice**: $c_{ij}$ = skalární součin i-tého řádku A a j-tého sloupce B
- **Pravidlo rozměrů**: $(m \times n) \cdot (n \times p) = (m \times p)$
- Vnitřní rozměry musí souhlasit!
- Násobení **NENÍ** komutativní: $\mathbf{AB} \neq \mathbf{BA}$
- V NumPy: operátor `@` nebo `np.dot()`
- Neuronová síť: $\mathbf{y} = \mathbf{Wx} + \mathbf{b}$
:::
V další kapitole uvidíme, jak matice reprezentují **transformace** -- rotace, škálování a další geometrické operace.