# Informace a entropie {#sec-entropie}
## Motivace: Kolik informace je ve zprávě?
Představte si dvě zprávy:
1. "Zítra bude v Praze počasí." (samozřejmé)
2. "Zítra bude v Praze sněžit." (v létě - překvapivé!)
Druhá zpráva nese více **informace**, protože je překvapivější. Tuto intuici formalizoval Claude Shannon v roce 1948 a položil základy **teorie informace**.
V strojovém učení je entropie klíčová pro:
- **Cross-entropy loss** - nejpoužívanější loss funkce pro klasifikaci
- **Perplexita** - míra kvality jazykových modelů
- **KL divergence** - měření rozdílu mezi rozděleními
- **Informační zisk** - rozhodovací stromy
## Co je informace?
Intuitivně: čím méně pravděpodobná událost, tím více informace nese.
::: {.callout-note}
## Definice: Informace (překvapení)
**Informace** (nebo **překvapení**) spojená s událostí o pravděpodobnosti $p$ je:
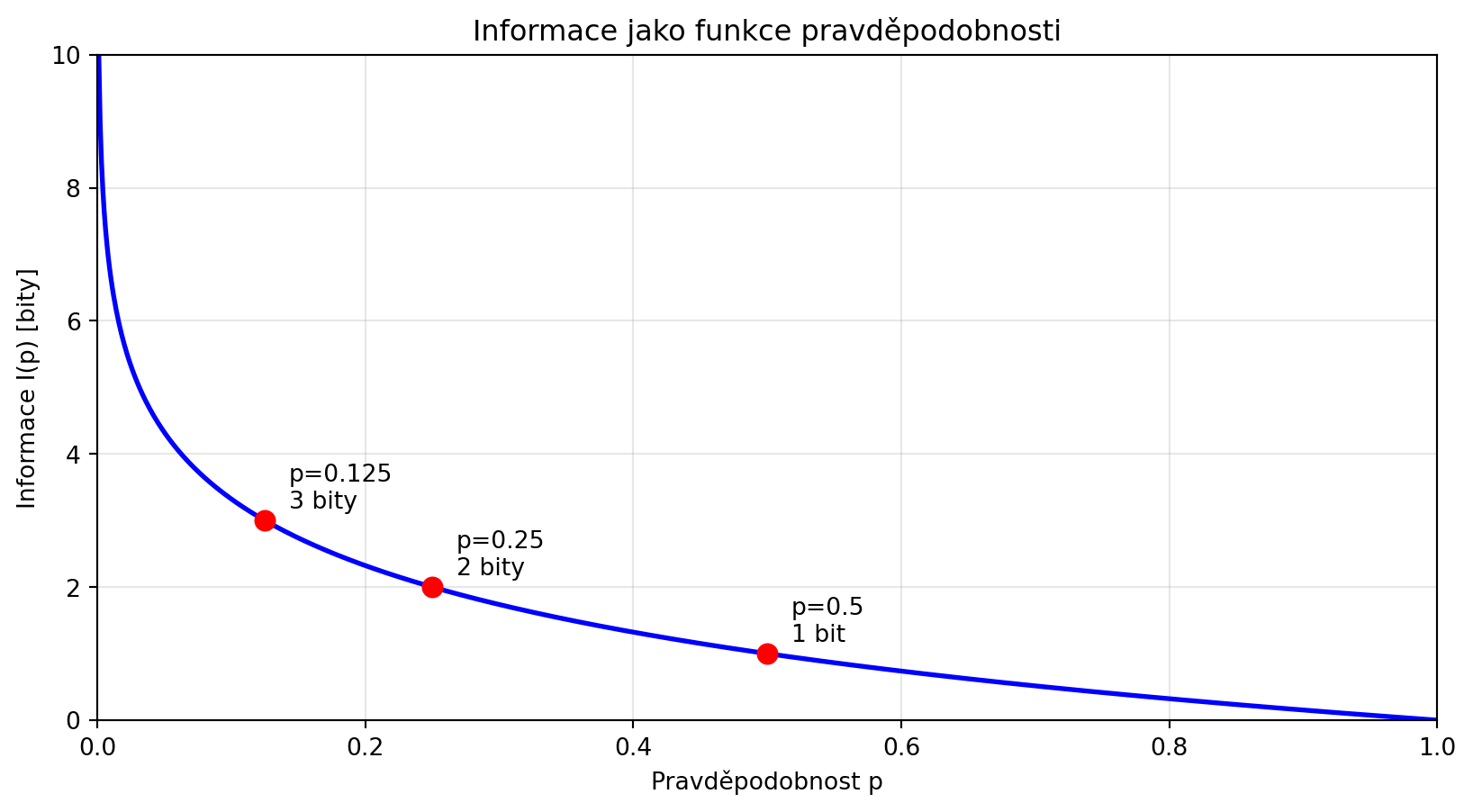
$$I(p) = -\log_2(p) = \log_2\left(\frac{1}{p}\right)$$
Jednotkou jsou **bity** (při použití logaritmu o základu 2).
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
def informace(p):
"""Informace v bitech pro pravděpodobnost p."""
return -np.log2(p)
# Příklady
print("Informace pro různé pravděpodobnosti:")
print("-" * 40)
for p in [1.0, 0.5, 0.25, 0.125, 0.1, 0.01, 0.001]:
if p > 0:
info = informace(p)
print(f"P = {p:<6} → I = {info:.3f} bitů")
# Vizualizace
p_range = np.linspace(0.001, 1, 1000)
info_range = informace(p_range)
plt.figure(figsize=(10, 5))
plt.plot(p_range, info_range, 'b-', lw=2)
plt.xlabel('Pravděpodobnost p')
plt.ylabel('Informace I(p) [bity]')
plt.title('Informace jako funkce pravděpodobnosti')
plt.grid(True, alpha=0.3)
plt.xlim(0, 1)
plt.ylim(0, 10)
# Vyznačení důležitých bodů
for p, label in [(0.5, 'p=0.5\n1 bit'), (0.25, 'p=0.25\n2 bity'), (0.125, 'p=0.125\n3 bity')]:
plt.plot(p, informace(p), 'ro', markersize=8)
plt.annotate(label, (p, informace(p)), textcoords="offset points", xytext=(10, 5))
plt.show()
```
### Proč logaritmus?
Logaritmus má speciální vlastnosti:
1. $I(1) = 0$ - jistá událost nese nula informace
2. $I(p) > 0$ pro $p < 1$ - nejistá událost nese pozitivní informaci
3. $I(p_1 \cdot p_2) = I(p_1) + I(p_2)$ - informace nezávislých událostí se sčítá
```{python}
# Příklad: Dva nezávislé hody mincí
p_panna = 0.5
p_dve_panny = 0.5 * 0.5
I_jedna = informace(p_panna)
I_dve = informace(p_dve_panny)
print(f"I(panna) = {I_jedna:.2f} bit")
print(f"I(dvě panny) = {I_dve:.2f} bity")
print(f"I(panna) + I(panna) = {2 * I_jedna:.2f} bity")
print(f"\nInformace se sčítá! ✓")
```
## Entropie
**Entropie** je průměrná (očekávaná) informace náhodné veličiny:
::: {.callout-note}
## Definice: Entropie
Pro diskrétní náhodnou veličinu $X$ s pravděpodobnostmi $p_1, p_2, \ldots, p_n$:
$$H(X) = -\sum_{i=1}^n p_i \log_2(p_i) = \sum_{i=1}^n p_i \cdot I(p_i)$$
Entropie měří **průměrnou nejistotu** nebo **průměrné překvapení**.
:::
```{python}
import numpy as np
def entropie(p):
"""Entropie rozdělení pravděpodobnosti."""
p = np.array(p)
p = p[p > 0] # Vyloučíme nuly (0 * log(0) = 0)
return -np.sum(p * np.log2(p))
# Příklad: Spravedlivá vs nefér mince
fer_mince = [0.5, 0.5]
nefer_mince = [0.9, 0.1]
velmi_nefer = [0.99, 0.01]
print("Entropie různých mincí:")
print(f"Férová (50/50): H = {entropie(fer_mince):.4f} bitů")
print(f"Neférová (90/10): H = {entropie(nefer_mince):.4f} bitů")
print(f"Velmi neférová (99/1): H = {entropie(velmi_nefer):.4f} bitů")
print(f"\nFérová mince má nejvyšší entropii = největší nejistotu")
```
### Entropie jako funkce pravděpodobnosti
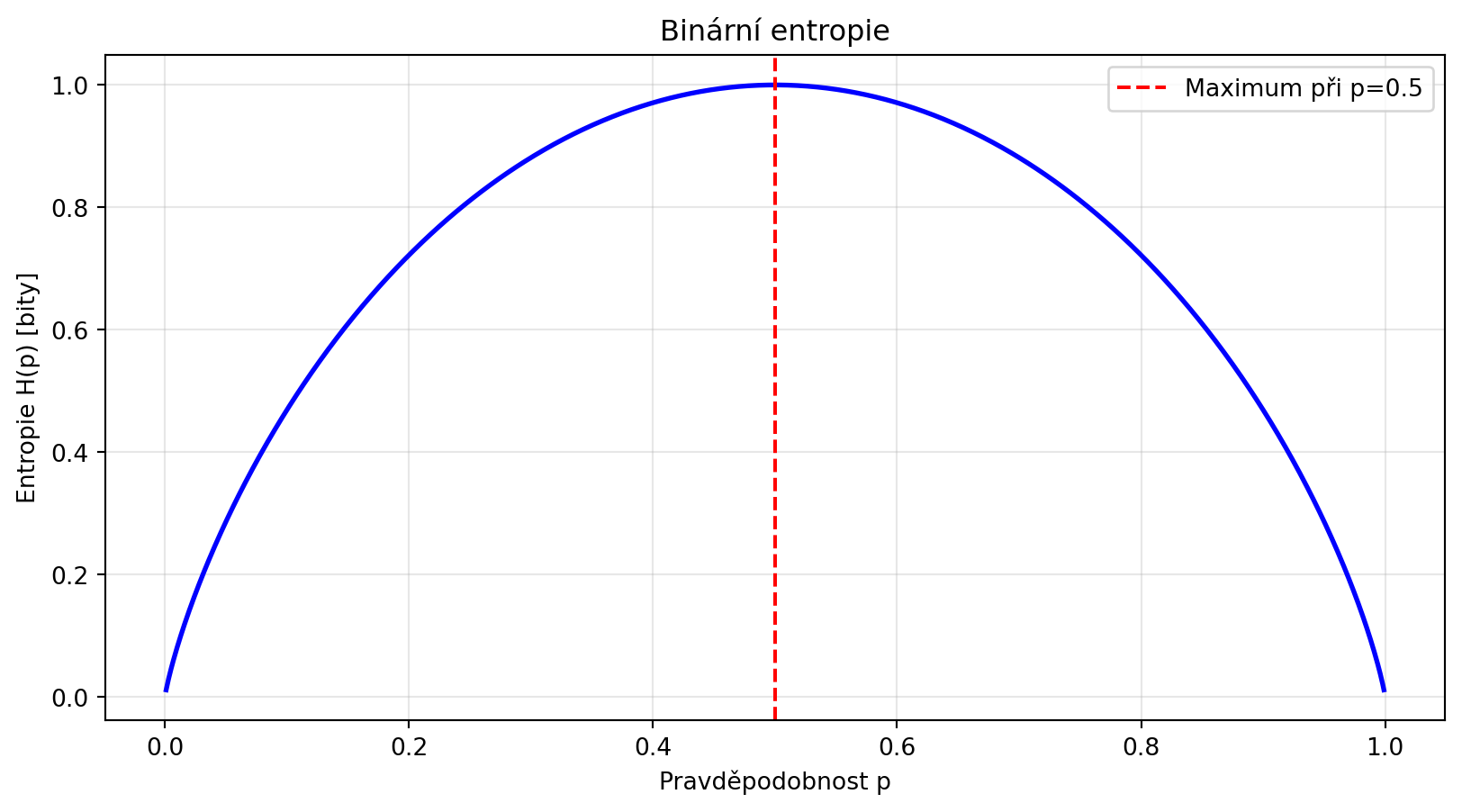
Pro binární případ ($p$ a $1-p$):
```{python}
import numpy as np
import matplotlib.pyplot as plt
def binarni_entropie(p):
"""Entropie binárního rozdělení."""
if p == 0 or p == 1:
return 0
return -p * np.log2(p) - (1-p) * np.log2(1-p)
p_range = np.linspace(0.001, 0.999, 1000)
H_range = [binarni_entropie(p) for p in p_range]
plt.figure(figsize=(10, 5))
plt.plot(p_range, H_range, 'b-', lw=2)
plt.xlabel('Pravděpodobnost p')
plt.ylabel('Entropie H(p) [bity]')
plt.title('Binární entropie')
plt.grid(True, alpha=0.3)
plt.axvline(x=0.5, color='red', linestyle='--', label='Maximum při p=0.5')
plt.legend()
plt.show()
print("Binární entropie je maximální při p=0.5 (největší nejistota)")
print("a nulová při p=0 nebo p=1 (jistota)")
```
### Entropie kostky
```{python}
# Spravedlivá kostka
import numpy as np
import matplotlib.pyplot as plt
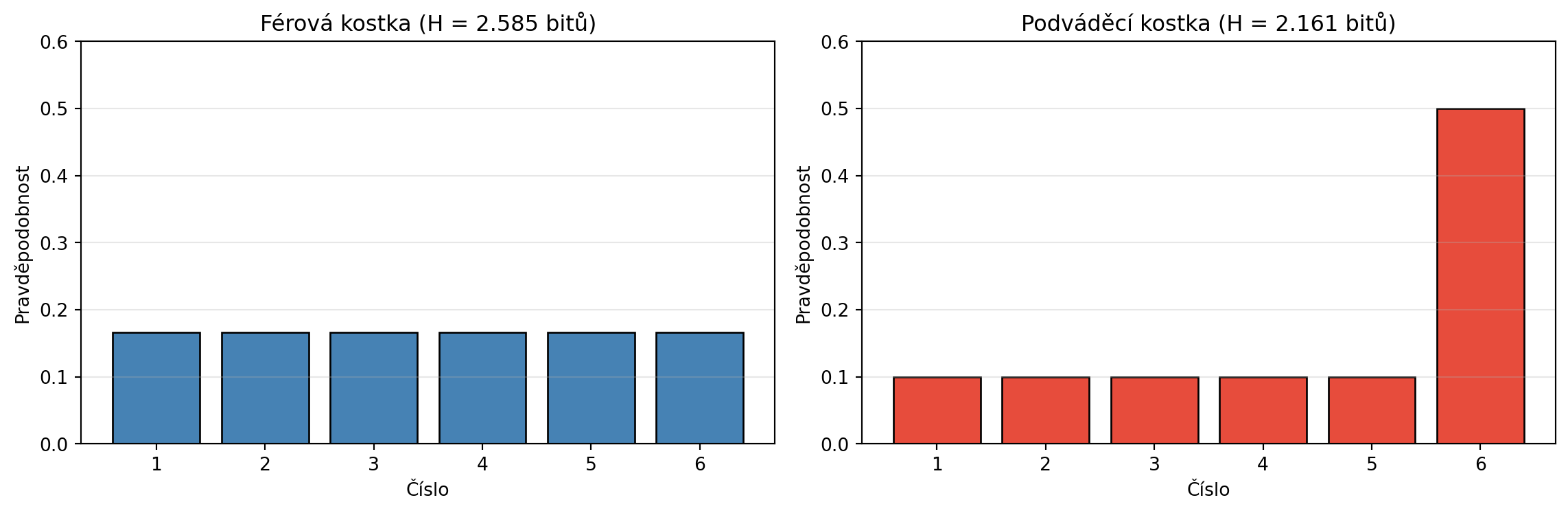
fer_kostka = [1/6] * 6
# "Podváděcí" kostka (6 padá častěji)
podvadeci_kostka = [0.1, 0.1, 0.1, 0.1, 0.1, 0.5]
H_fer = entropie(fer_kostka)
H_podvadeci = entropie(podvadeci_kostka)
print(f"Férová kostka: H = {H_fer:.4f} bitů = log₂(6) = {np.log2(6):.4f}")
print(f"Podváděcí kostka: H = {H_podvadeci:.4f} bitů")
print(f"\nMaximální entropie = log₂(n) pro rovnoměrné rozdělení")
# Vizualizace
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.bar(range(1, 7), fer_kostka, color='steelblue', edgecolor='black')
ax1.set_xlabel('Číslo')
ax1.set_ylabel('Pravděpodobnost')
ax1.set_title(f'Férová kostka (H = {H_fer:.3f} bitů)')
ax1.set_ylim(0, 0.6)
ax1.grid(axis='y', alpha=0.3)
ax2.bar(range(1, 7), podvadeci_kostka, color='#e74c3c', edgecolor='black')
ax2.set_xlabel('Číslo')
ax2.set_ylabel('Pravděpodobnost')
ax2.set_title(f'Podváděcí kostka (H = {H_podvadeci:.3f} bitů)')
ax2.set_ylim(0, 0.6)
ax2.grid(axis='y', alpha=0.3)
plt.tight_layout()
plt.show()
```
## Cross-entropy
**Cross-entropy** měří, kolik bitů potřebujeme k zakódování dat ze skutečného rozdělení $p$, pokud používáme kód optimalizovaný pro rozdělení $q$:
::: {.callout-note}
## Definice: Cross-entropy
$$H(p, q) = -\sum_i p_i \log_2(q_i)$$
kde $p$ je skutečné rozdělení a $q$ je predikované rozdělení.
:::
```{python}
import numpy as np
def cross_entropie(p, q):
"""Cross-entropy mezi rozděleními p a q."""
p = np.array(p)
q = np.array(q)
# Ošetření log(0)
q = np.clip(q, 1e-15, 1)
return -np.sum(p * np.log2(q))
# Příklad: Klasifikace
# Skutečné rozdělení (one-hot): třída 0
p_true = [1, 0, 0]
# Různé predikce modelu
q_good = [0.9, 0.05, 0.05] # Dobrá predikce
q_bad = [0.3, 0.4, 0.3] # Špatná predikce
q_terrible = [0.1, 0.1, 0.8] # Hrozná predikce (jistá, ale špatně)
print("Cross-entropy pro různé predikce:")
print(f"Skutečná třída: 0 (one-hot: {p_true})")
print("-" * 50)
print(f"Dobrá predikce {q_good}: CE = {cross_entropie(p_true, q_good):.4f}")
print(f"Špatná predikce {q_bad}: CE = {cross_entropie(p_true, q_bad):.4f}")
print(f"Hrozná predikce {q_terrible}: CE = {cross_entropie(p_true, q_terrible):.4f}")
print("\nNižší cross-entropy = lepší model!")
```
### Cross-entropy jako loss funkce
V klasifikaci používáme cross-entropy jako loss funkci:
```{python}
import torch
import torch.nn as nn
# PyTorch CrossEntropyLoss
criterion = nn.CrossEntropyLoss()
# Logity (výstupy sítě před softmax)
logits = torch.tensor([[2.0, 1.0, 0.1]]) # Predikce pro jeden vzorek
target = torch.tensor([0]) # Skutečná třída je 0
loss = criterion(logits, target)
print(f"PyTorch CrossEntropyLoss: {loss.item():.4f}")
# Ruční výpočet
probs = torch.softmax(logits, dim=1)
print(f"Softmax pravděpodobnosti: {probs.numpy()[0]}")
# Cross-entropy = -log(p[správná třída])
manual_loss = -torch.log(probs[0, target[0]])
print(f"Ruční výpočet: {manual_loss.item():.4f}")
```
### Vizualizace cross-entropy loss
```{python}
# Jak se mění loss s pravděpodobností správné třídy
import numpy as np
import matplotlib.pyplot as plt
p_correct = np.linspace(0.01, 0.99, 100)
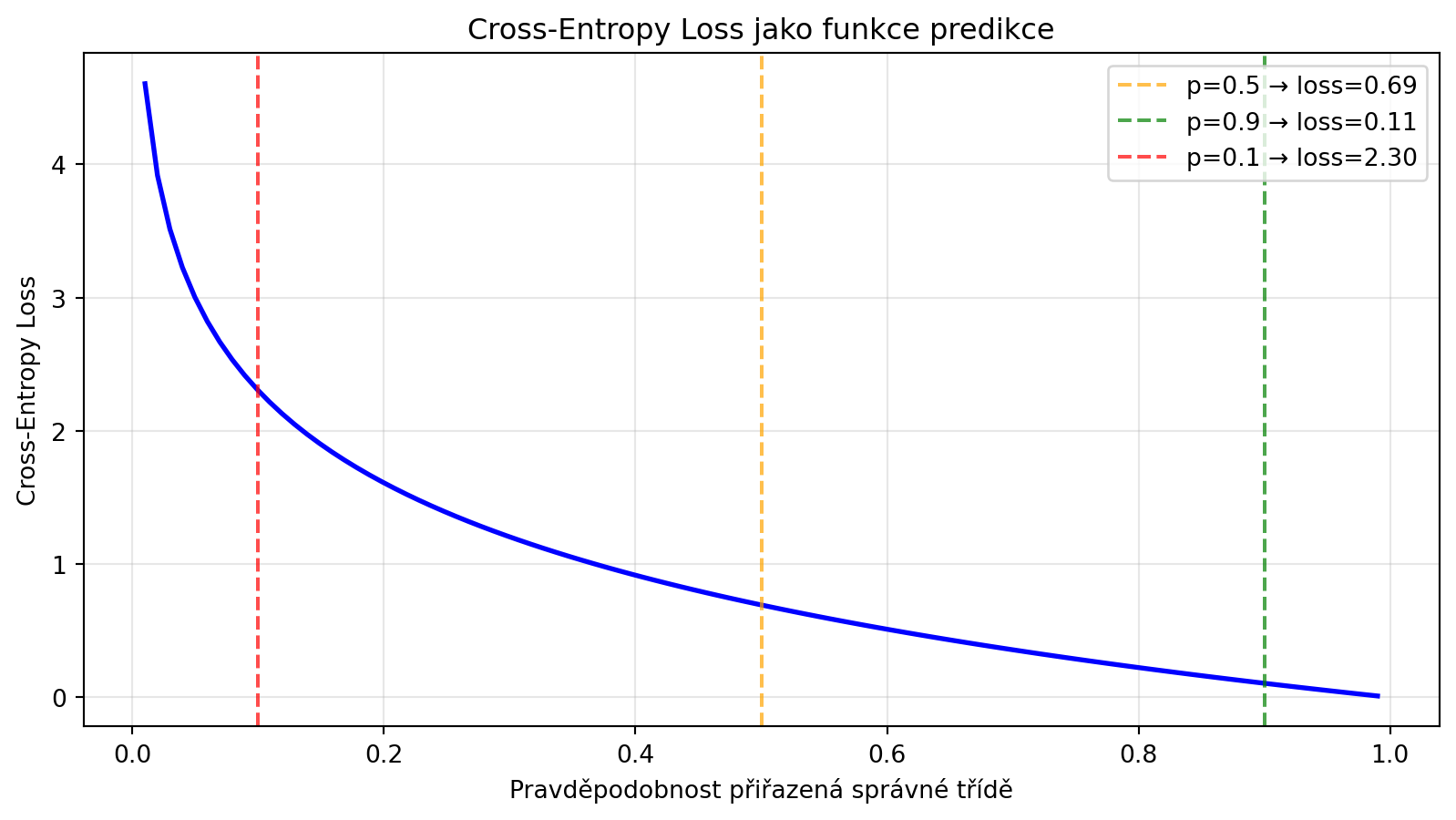
ce_loss = -np.log(p_correct) # Používáme přirozený logaritmus (jako PyTorch)
plt.figure(figsize=(10, 5))
plt.plot(p_correct, ce_loss, 'b-', lw=2)
plt.xlabel('Pravděpodobnost přiřazená správné třídě')
plt.ylabel('Cross-Entropy Loss')
plt.title('Cross-Entropy Loss jako funkce predikce')
plt.grid(True, alpha=0.3)
# Důležité body
plt.axvline(x=0.5, color='orange', linestyle='--', alpha=0.7, label='p=0.5 → loss=0.69')
plt.axvline(x=0.9, color='green', linestyle='--', alpha=0.7, label='p=0.9 → loss=0.11')
plt.axvline(x=0.1, color='red', linestyle='--', alpha=0.7, label='p=0.1 → loss=2.30')
plt.legend()
plt.show()
print("Cross-entropy prudce roste, když model přiřadí nízkou pravděpodobnost správné třídě")
```
## KL Divergence
**Kullback-Leibler divergence** měří, jak moc se rozdělení $q$ liší od $p$:
::: {.callout-note}
## Definice: KL Divergence
$$D_{KL}(p \| q) = \sum_i p_i \log\left(\frac{p_i}{q_i}\right) = H(p, q) - H(p)$$
KL divergence je "extra bity" potřebné kvůli použití $q$ místo $p$.
:::
```{python}
import numpy as np
def kl_divergence(p, q):
"""KL divergence D_KL(p || q)."""
p = np.array(p)
q = np.array(q)
# Ošetření 0/0 a log(0)
mask = p > 0
p = p[mask]
q = q[mask]
q = np.clip(q, 1e-15, 1)
return np.sum(p * np.log2(p / q))
# Příklad
p = [0.5, 0.3, 0.2]
q1 = [0.5, 0.3, 0.2] # Stejné jako p
q2 = [0.4, 0.35, 0.25] # Blízké p
q3 = [0.2, 0.2, 0.6] # Vzdálené od p
print(f"p = {p}")
print("-" * 40)
print(f"D_KL(p || q1={q1}) = {kl_divergence(p, q1):.6f}")
print(f"D_KL(p || q2={q2}) = {kl_divergence(p, q2):.6f}")
print(f"D_KL(p || q3={q3}) = {kl_divergence(p, q3):.6f}")
# Asymetrie KL divergence
print(f"\nAsymetrie:")
print(f"D_KL(p || q3) = {kl_divergence(p, q3):.4f}")
print(f"D_KL(q3 || p) = {kl_divergence(q3, p):.4f}")
print("KL divergence není symetrická!")
```
### Vztah mezi entropií, cross-entropií a KL divergencí
```{python}
import numpy as np
import matplotlib.pyplot as plt
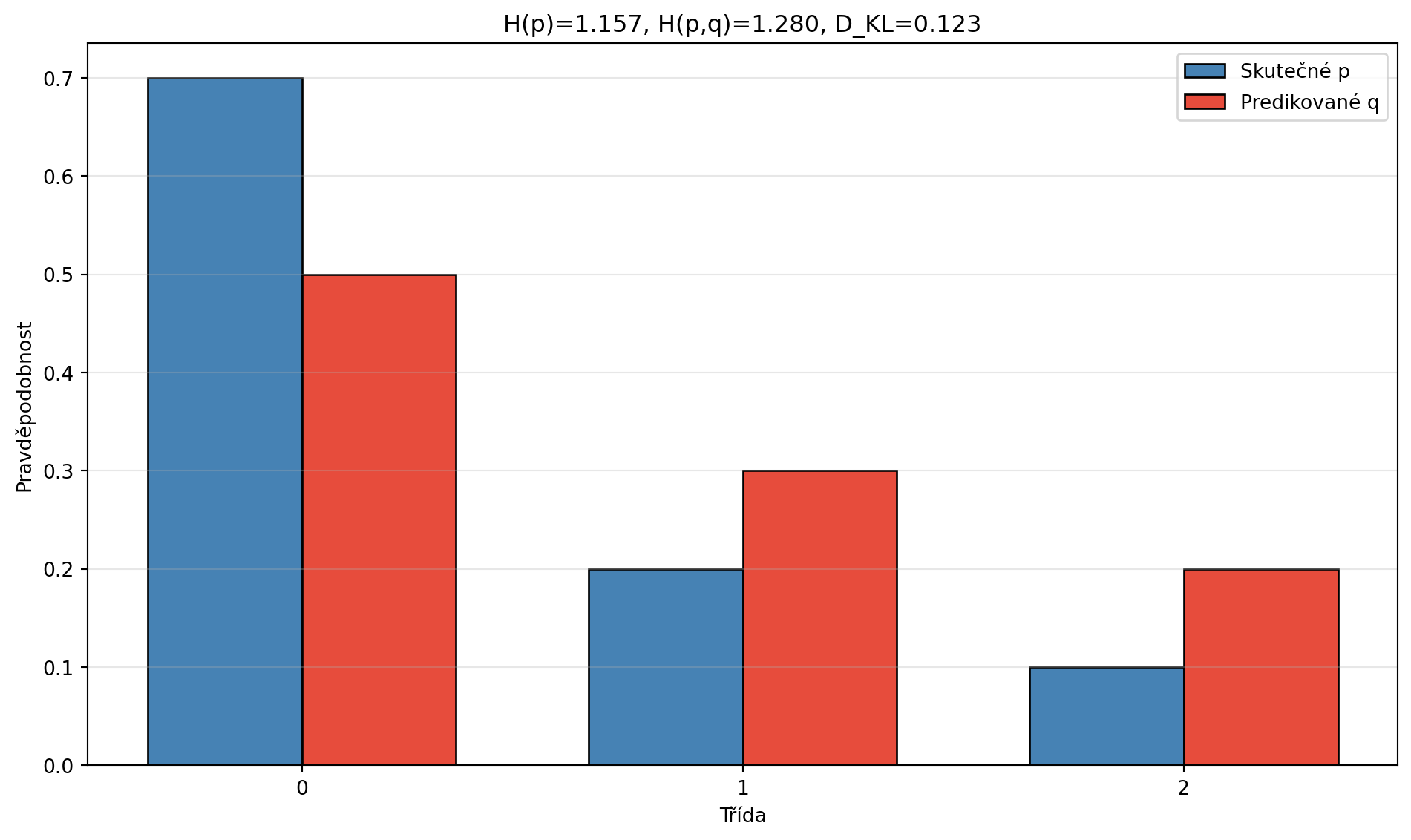
p = [0.7, 0.2, 0.1]
q = [0.5, 0.3, 0.2]
H_p = entropie(p)
H_pq = cross_entropie(p, q)
D_KL = kl_divergence(p, q)
print(f"p = {p}")
print(f"q = {q}")
print("-" * 40)
print(f"Entropie H(p) = {H_p:.4f}")
print(f"Cross-entropy H(p,q) = {H_pq:.4f}")
print(f"KL divergence D_KL(p||q) = {D_KL:.4f}")
print(f"\nOvěření: H(p,q) = H(p) + D_KL(p||q)")
print(f"{H_pq:.4f} = {H_p:.4f} + {D_KL:.4f} = {H_p + D_KL:.4f} ✓")
# Vizualizace
fig, ax = plt.subplots(figsize=(10, 6))
x = np.arange(3)
width = 0.35
bars1 = ax.bar(x - width/2, p, width, label='Skutečné p', color='steelblue', edgecolor='black')
bars2 = ax.bar(x + width/2, q, width, label='Predikované q', color='#e74c3c', edgecolor='black')
ax.set_ylabel('Pravděpodobnost')
ax.set_xlabel('Třída')
ax.set_title(f'H(p)={H_p:.3f}, H(p,q)={H_pq:.3f}, D_KL={D_KL:.3f}')
ax.set_xticks(x)
ax.legend()
ax.grid(axis='y', alpha=0.3)
plt.tight_layout()
plt.show()
```
## Perplexita
**Perplexita** je míra kvality jazykových modelů - měří, jak "překvapený" je model pozorovanými daty:
::: {.callout-note}
## Definice: Perplexita
$$\text{PPL} = 2^{H(p, q)}$$
kde $H(p, q)$ je cross-entropy mezi skutečným a predikovaným rozdělením.
Pro sekvenci slov délky $N$:
$$\text{PPL} = \exp\left(-\frac{1}{N}\sum_{i=1}^N \log P(w_i | w_{<i})\right)$$
:::
```{python}
def perplexita(cross_entropy):
"""Perplexita z cross-entropy."""
return 2 ** cross_entropy
# Příklad: Jazykový model
# Predikce pro slovo po "The cat"
p_true = [0, 0, 0, 1, 0] # Skutečné slovo: "sat" (index 3)
slova = ['the', 'a', 'dog', 'sat', 'ran']
# Různé modely
q_good = [0.05, 0.05, 0.1, 0.7, 0.1] # Dobrý model
q_medium = [0.1, 0.1, 0.2, 0.4, 0.2] # Střední model
q_bad = [0.2, 0.2, 0.2, 0.2, 0.2] # Špatný model (náhodný)
modely = [("Dobrý", q_good), ("Střední", q_medium), ("Špatný", q_bad)]
print("Perplexita různých jazykových modelů:")
print("-" * 50)
for nazev, q in modely:
ce = cross_entropie(p_true, q)
ppl = perplexita(ce)
print(f"{nazev:10} model: CE = {ce:.3f} bitů, PPL = {ppl:.2f}")
print("\nNižší perplexita = lepší model")
print("PPL ≈ počet možností, mezi kterými model 'váhá'")
```
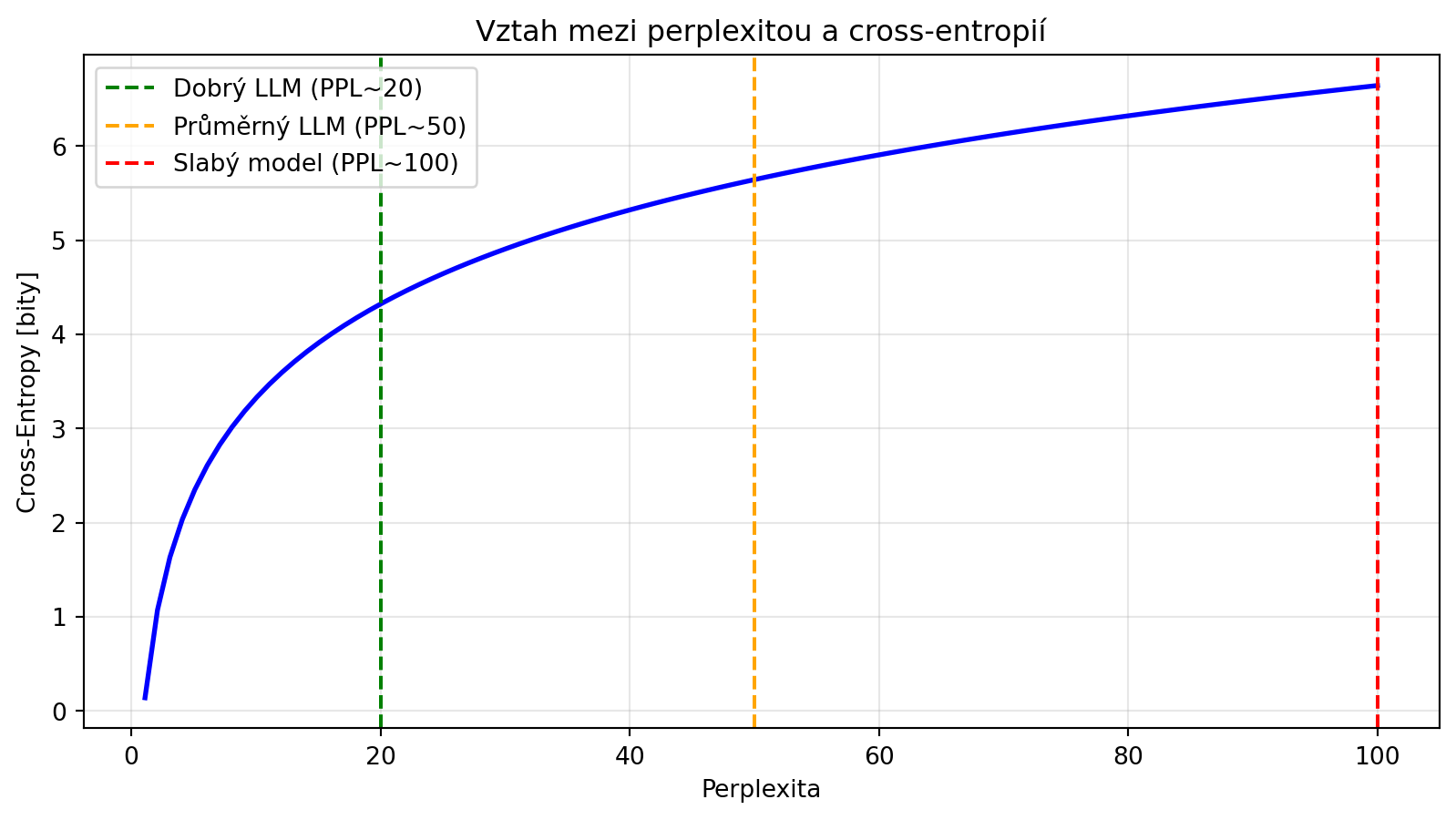
### Interpretace perplexity
```{python}
# Perplexita jako "efektivní počet možností"
import numpy as np
import matplotlib.pyplot as plt
perplexity_values = [2, 10, 100, 1000, 10000]
print("Interpretace perplexity:")
print("-" * 50)
for ppl in perplexity_values:
print(f"PPL = {ppl:5}: Model je 'nejistý' jako při výběru z ~{ppl} možností")
# Vizualizace
ppl_range = np.linspace(1.1, 100, 100)
ce_range = np.log2(ppl_range)
plt.figure(figsize=(10, 5))
plt.plot(ppl_range, ce_range, 'b-', lw=2)
plt.xlabel('Perplexita')
plt.ylabel('Cross-Entropy [bity]')
plt.title('Vztah mezi perplexitou a cross-entropií')
plt.grid(True, alpha=0.3)
# Typické hodnoty pro jazykové modely
plt.axvline(x=20, color='green', linestyle='--', label='Dobrý LLM (PPL~20)')
plt.axvline(x=50, color='orange', linestyle='--', label='Průměrný LLM (PPL~50)')
plt.axvline(x=100, color='red', linestyle='--', label='Slabý model (PPL~100)')
plt.legend()
plt.show()
```
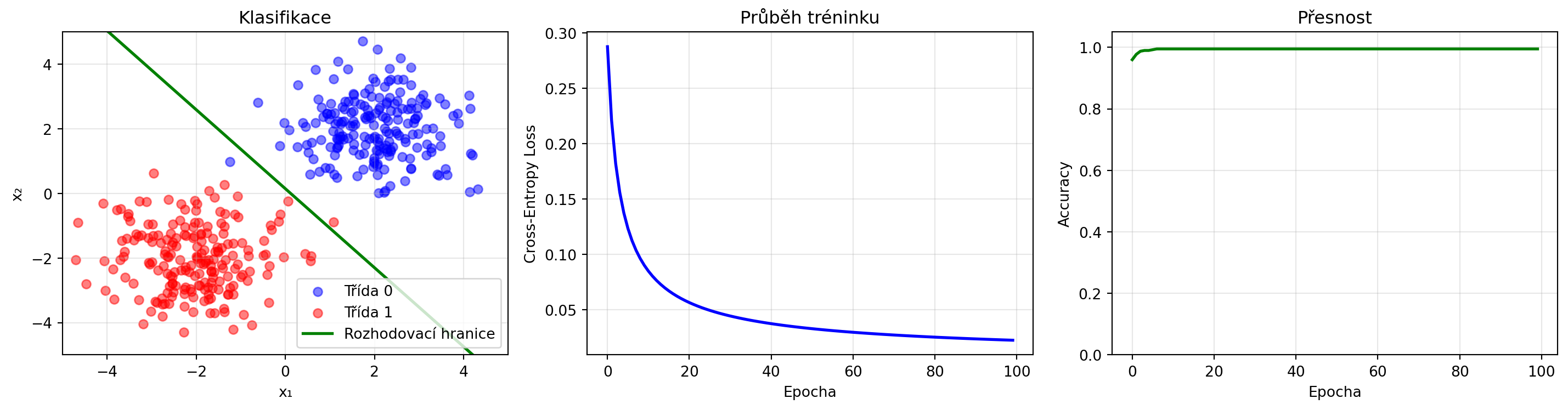
## Aplikace: Trénink klasifikátoru
Pojďme vidět cross-entropy loss v akci:
```{python}
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
# Syntetická data pro binární klasifikaci
np.random.seed(42)
torch.manual_seed(42)
# Dvě třídy
n_samples = 200
X0 = np.random.randn(n_samples, 2) + np.array([2, 2])
X1 = np.random.randn(n_samples, 2) + np.array([-2, -2])
X = np.vstack([X0, X1])
y = np.array([0] * n_samples + [1] * n_samples)
# Převod na PyTorch tensory
X_tensor = torch.FloatTensor(X)
y_tensor = torch.LongTensor(y)
# Jednoduchý model
class Klasifikator(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(2, 2)
def forward(self, x):
return self.linear(x)
model = Klasifikator()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)
# Trénink
losses = []
accuracies = []
for epoch in range(100):
# Forward
outputs = model(X_tensor)
loss = criterion(outputs, y_tensor)
# Backward
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Metriky
_, predicted = torch.max(outputs, 1)
accuracy = (predicted == y_tensor).float().mean()
losses.append(loss.item())
accuracies.append(accuracy.item())
# Vizualizace
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# Data a rozhodovací hranice
ax = axes[0]
ax.scatter(X[y==0, 0], X[y==0, 1], c='blue', alpha=0.5, label='Třída 0')
ax.scatter(X[y==1, 0], X[y==1, 1], c='red', alpha=0.5, label='Třída 1')
# Rozhodovací hranice
w = model.linear.weight.detach().numpy()
b = model.linear.bias.detach().numpy()
x_line = np.linspace(-5, 5, 100)
# w[0]x + w[1]y + b = 0 pro obě třídy
# Hledáme kde jsou logity stejné
y_line = -(w[0,0] - w[1,0]) * x_line / (w[0,1] - w[1,1]) - (b[0] - b[1]) / (w[0,1] - w[1,1])
ax.plot(x_line, y_line, 'g-', lw=2, label='Rozhodovací hranice')
ax.set_xlabel('x₁')
ax.set_ylabel('x₂')
ax.set_title('Klasifikace')
ax.legend()
ax.set_xlim(-5, 5)
ax.set_ylim(-5, 5)
ax.grid(True, alpha=0.3)
# Loss
axes[1].plot(losses, 'b-', lw=2)
axes[1].set_xlabel('Epocha')
axes[1].set_ylabel('Cross-Entropy Loss')
axes[1].set_title('Průběh tréninku')
axes[1].grid(True, alpha=0.3)
# Accuracy
axes[2].plot(accuracies, 'g-', lw=2)
axes[2].set_xlabel('Epocha')
axes[2].set_ylabel('Accuracy')
axes[2].set_title('Přesnost')
axes[2].set_ylim(0, 1.05)
axes[2].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print(f"Finální loss: {losses[-1]:.4f}")
print(f"Finální accuracy: {accuracies[-1]:.2%}")
```
## Řešené příklady
### Příklad 1: Výpočet entropie
**Zadání**: Spočítejte entropii rozdělení $p = (0.5, 0.25, 0.125, 0.125)$.
**Řešení**:
```{python}
import numpy as np
p = [0.5, 0.25, 0.125, 0.125]
# Ruční výpočet
H = 0
for pi in p:
H -= pi * np.log2(pi)
print("Ruční výpočet:")
for pi in p:
print(f" {pi} × log₂({pi}) = {pi} × {np.log2(pi):.3f} = {pi * np.log2(pi):.3f}")
print(f" H = {H:.4f} bitů")
# Ověření
print(f"\nOvěření funkcí: H = {entropie(p):.4f} bitů")
```
### Příklad 2: Porovnání modelů pomocí cross-entropy
**Zadání**: Máme dva modely pro předpověď počasí. Skutečné pravděpodobnosti jsou slunečno=60%, zataženo=30%, déšť=10%. Model A predikuje 50%, 30%, 20%. Model B predikuje 70%, 20%, 10%. Který je lepší?
**Řešení**:
```{python}
p_true = [0.6, 0.3, 0.1]
q_A = [0.5, 0.3, 0.2]
q_B = [0.7, 0.2, 0.1]
CE_A = cross_entropie(p_true, q_A)
CE_B = cross_entropie(p_true, q_B)
print(f"Skutečné rozdělení: {p_true}")
print(f"Model A: {q_A}")
print(f"Model B: {q_B}")
print("-" * 40)
print(f"Cross-entropy A: {CE_A:.4f}")
print(f"Cross-entropy B: {CE_B:.4f}")
print(f"\nLepší je Model {'A' if CE_A < CE_B else 'B'} (nižší cross-entropy)")
# KL divergence
KL_A = kl_divergence(p_true, q_A)
KL_B = kl_divergence(p_true, q_B)
print(f"\nKL divergence A: {KL_A:.4f}")
print(f"KL divergence B: {KL_B:.4f}")
```
### Příklad 3: Perplexita jazykového modelu
**Zadání**: Jazyková model přiřadil větě "The cat sat" následující pravděpodobnosti: P("The")=0.1, P("cat"|"The")=0.3, P("sat"|"The cat")=0.5. Jaká je perplexita?
**Řešení**:
```{python}
# Pravděpodobnosti jednotlivých slov
import numpy as np
probs = [0.1, 0.3, 0.5]
N = len(probs)
# Log-likelihood
log_likelihood = sum(np.log(p) for p in probs)
# Průměrná log-likelihood
avg_log_likelihood = log_likelihood / N
# Perplexita
ppl = np.exp(-avg_log_likelihood)
print(f"Pravděpodobnosti: {probs}")
print(f"Log-likelihood: {log_likelihood:.4f}")
print(f"Průměrná log-likelihood: {avg_log_likelihood:.4f}")
print(f"Perplexita: {ppl:.2f}")
# Alternativní výpočet
ppl_alt = (np.prod(probs)) ** (-1/N)
print(f"Alternativní výpočet: {ppl_alt:.2f}")
```
### Příklad 4: Informační zisk
**Zadání**: V rozhodovacím stromu chceme rozdělit data podle atributu. Spočítejte informační zisk.
**Řešení**:
```{python}
# Původní data: 10 pozitivních, 10 negativních
p_parent = [0.5, 0.5]
H_parent = entropie(p_parent)
# Po rozdělení podle atributu:
# Levá větev: 8 pozitivních, 2 negativní (10 vzorků)
# Pravá větev: 2 pozitivní, 8 negativních (10 vzorků)
p_left = [0.8, 0.2]
p_right = [0.2, 0.8]
H_left = entropie(p_left)
H_right = entropie(p_right)
# Vážený průměr entropie po rozdělení
w_left = 10/20
w_right = 10/20
H_after = w_left * H_left + w_right * H_right
# Informační zisk
info_gain = H_parent - H_after
print(f"Entropie před rozdělením: H = {H_parent:.4f}")
print(f"Entropie levé větve: H = {H_left:.4f}")
print(f"Entropie pravé větve: H = {H_right:.4f}")
print(f"Vážená entropie po rozdělení: H = {H_after:.4f}")
print(f"\nInformační zisk: {info_gain:.4f} bitů")
```
### Příklad 5: Multiclass klasifikace
**Zadání**: Implementujte cross-entropy loss pro multiclass klasifikaci a vizualizujte gradient.
**Řešení**:
```{python}
import numpy as np
def softmax(z):
exp_z = np.exp(z - np.max(z))
return exp_z / np.sum(exp_z)
def cross_entropy_loss(logits, target):
"""Cross-entropy loss pro jeden vzorek."""
probs = softmax(logits)
return -np.log(probs[target])
def cross_entropy_gradient(logits, target):
"""Gradient cross-entropy loss vzhledem k logitům."""
probs = softmax(logits)
grad = probs.copy()
grad[target] -= 1
return grad
# Příklad
logits = np.array([2.0, 1.0, 0.5])
target = 0 # Správná třída
probs = softmax(logits)
loss = cross_entropy_loss(logits, target)
grad = cross_entropy_gradient(logits, target)
print(f"Logity: {logits}")
print(f"Softmax: {probs}")
print(f"Správná třída: {target}")
print(f"Loss: {loss:.4f}")
print(f"Gradient: {grad}")
print(f"\nGradient = softmax - one_hot")
print(f"Pro správnou třídu: grad[0] = {probs[0]:.3f} - 1 = {grad[0]:.3f}")
print(f"Pro ostatní: grad[1] = {probs[1]:.3f} - 0 = {grad[1]:.3f}")
```
## Python v praxi: PyTorch loss funkce
```{python}
import torch
import torch.nn as nn
# Vytvoření dat
batch_size = 4
num_classes = 5
# Náhodné logity a cíle
logits = torch.randn(batch_size, num_classes)
targets = torch.randint(0, num_classes, (batch_size,))
print("Logity (výstupy sítě):")
print(logits)
print(f"\nCíle: {targets}")
# Cross-Entropy Loss
criterion = nn.CrossEntropyLoss()
loss = criterion(logits, targets)
print(f"\nCross-Entropy Loss: {loss.item():.4f}")
# Ekvivalentní: NLLLoss + LogSoftmax
log_softmax = nn.LogSoftmax(dim=1)
nll_loss = nn.NLLLoss()
loss_alt = nll_loss(log_softmax(logits), targets)
print(f"NLLLoss + LogSoftmax: {loss_alt.item():.4f}")
# Pro binární klasifikaci: BCEWithLogitsLoss
binary_logits = torch.randn(batch_size)
binary_targets = torch.randint(0, 2, (batch_size,)).float()
bce_criterion = nn.BCEWithLogitsLoss()
bce_loss = bce_criterion(binary_logits, binary_targets)
print(f"\nBCE Loss (binární): {bce_loss.item():.4f}")
```
## Cvičení
::: {.callout-note icon=false}
## Cvičení 1: Entropie
Spočítejte entropii:
a) Rovnoměrného rozdělení na 8 výsledcích
b) Rozdělení [0.9, 0.05, 0.05]
c) Jaké rozdělení na 3 výsledcích má maximální entropii?
:::
::: {.callout-note icon=false}
## Cvičení 2: Cross-entropy
Model přiřadil třídám pravděpodobnosti [0.7, 0.2, 0.1]. Skutečná třída je 0. Spočítejte cross-entropy loss. Jak by se loss změnila, kdyby skutečná třída byla 2?
:::
::: {.callout-note icon=false}
## Cvičení 3: KL divergence
Dokažte, že KL divergence je vždy nezáporná (Jensen inequality). Simulujte to pro náhodná rozdělení.
:::
::: {.callout-note icon=false}
## Cvičení 4: Perplexita
Jazyková model má perplexitu 25 na testovací sadě. Co to znamená intuitivně? Jaká by byla perplexita modelu, který by pouze náhodně vybíral z 10000 slov slovníku?
:::
::: {.callout-note icon=false}
## Cvičení 5: Label smoothing
Implementujte "label smoothing" - místo one-hot vektorů používáme měkké labely jako [0.9, 0.05, 0.05]. Jak to ovlivní trénink?
:::
::: {.callout-note icon=false}
## Cvičení 6: Focal Loss
Implementujte Focal Loss: $FL = -\alpha(1-p_t)^\gamma \log(p_t)$, která klade větší důraz na obtížné vzorky. Porovnejte s běžnou cross-entropy.
:::
## Shrnutí
::: {.callout-tip}
## Co jsme se naučili
1. **Informace** $I(p) = -\log_2(p)$ měří překvapení z události
2. **Entropie** $H(X) = -\sum p_i \log_2(p_i)$ je průměrná nejistota
3. **Cross-entropy** $H(p,q) = -\sum p_i \log_2(q_i)$ měří kvalitu predikce
4. **KL divergence** $D_{KL}(p||q) = H(p,q) - H(p)$ měří rozdíl mezi rozděleními
5. **Cross-entropy loss** je standardní loss funkce pro klasifikaci
6. **Perplexita** $2^{H(p,q)}$ měří kvalitu jazykových modelů
:::
::: {.callout-important}
## Klíčové vzorce
- **Informace**: $I(p) = -\log_2(p)$
- **Entropie**: $H(X) = -\sum_i p_i \log_2(p_i)$
- **Cross-entropy**: $H(p,q) = -\sum_i p_i \log_2(q_i)$
- **KL divergence**: $D_{KL}(p||q) = \sum_i p_i \log_2(p_i/q_i)$
- **Perplexita**: $\text{PPL} = 2^{H(p,q)}$
:::
Tímto končíme část o pravděpodobnosti. V další části se podíváme na optimalizaci - jak používat gradienty k minimalizaci loss funkcí a trénování modelů.