# Souřadnicový systém
::: {.callout-tip title="Co se naučíte"}
V této kapitole se naučíte:
- Co je kartézská soustava souřadnic
- Jak zapisovat a zobrazovat body v rovině
- Jak vypočítat vzdálenost mezi dvěma body
- Jak pracovat se souřadnicemi v Pythonu
:::
## Proč potřebujeme souřadnice?
Představte si, že hrajete hru, kde ovládáte postavu na obrazovce. Jak počítač ví, kde postava je? Používá **souřadnice** -- dvojici čísel, která přesně určuje pozici.
Souřadnice používáme všude:
- **GPS navigace** -- určuje pozici jako zeměpisnou šířku a délku
- **Počítačová grafika** -- každý pixel má své souřadnice
- **Mapy v hrách** -- pozice postav, nepřátel, pokladů
- **Strojové učení** -- data jsou body v prostoru souřadnic
::: {.callout-note title="Historická poznámka"}
Souřadnicový systém vynalezl francouzský filosof a matematik **René Descartes** (1596-1650). Proto se mu říká **kartézská** soustava souřadnic (z latinské podoby jeho jména: Cartesius).
:::
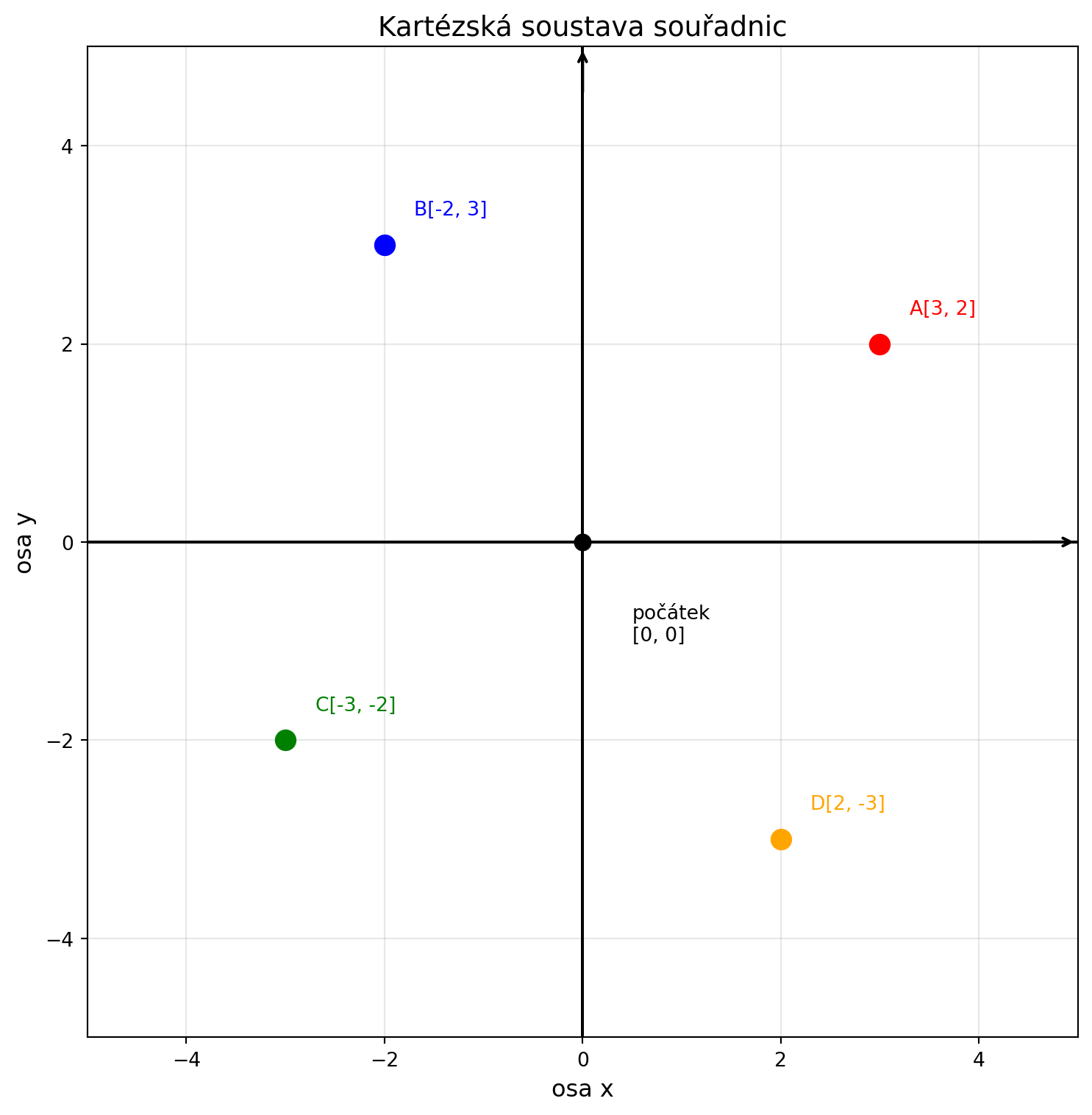
## Kartézská soustava souřadnic
Kartézská soustava souřadnic se skládá ze dvou os:
- **Osa x** (vodorovná) -- běží zleva doprava
- **Osa y** (svislá) -- běží zdola nahoru
Osy se protínají v **počátku** (anglicky *origin*), který má souřadnice [0, 0].
```{python}
#| fig-cap: "Kartézská soustava souřadnic"
#| code-fold: true
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 8))
# Osy
ax.axhline(y=0, color='k', linewidth=1.5)
ax.axvline(x=0, color='k', linewidth=1.5)
# Mřížka
ax.grid(True, alpha=0.3)
ax.set_xlim(-5, 5)
ax.set_ylim(-5, 5)
# Popisky os
ax.set_xlabel('osa x', fontsize=12)
ax.set_ylabel('osa y', fontsize=12)
# Šipky na koncích os
ax.annotate('', xy=(5, 0), xytext=(4.5, 0),
arrowprops=dict(arrowstyle='->', color='black', lw=1.5))
ax.annotate('', xy=(0, 5), xytext=(0, 4.5),
arrowprops=dict(arrowstyle='->', color='black', lw=1.5))
# Počátek
ax.plot(0, 0, 'ko', markersize=8)
ax.annotate('počátek\n[0, 0]', xy=(0, 0), xytext=(0.5, -1),
fontsize=10, ha='left')
# Ukázkové body
body = [(3, 2), (-2, 3), (-3, -2), (2, -3)]
barvy = ['red', 'blue', 'green', 'orange']
nazvy = ['A[3, 2]', 'B[-2, 3]', 'C[-3, -2]', 'D[2, -3]']
for (x, y), barva, nazev in zip(body, barvy, nazvy):
ax.plot(x, y, 'o', color=barva, markersize=10)
ax.annotate(nazev, xy=(x, y), xytext=(x+0.3, y+0.3),
fontsize=10, color=barva)
ax.set_aspect('equal')
ax.set_title('Kartézská soustava souřadnic', fontsize=14)
plt.tight_layout()
plt.show()
```
## Body v rovině
Každý bod v rovině má dvě souřadnice:
- **x-ová souřadnice** -- říká, jak daleko je bod od osy y (vpravo = kladné, vlevo = záporné)
- **y-ová souřadnice** -- říká, jak daleko je bod od osy x (nahoru = kladné, dolů = záporné)
Bod zapisujeme jako **[x, y]** nebo **(x, y)**.
::: {.callout-note title="Příklad"}
Bod **A[3, 2]** znamená:
- Jdi 3 jednotky doprava (x = 3)
- Jdi 2 jednotky nahoru (y = 2)
:::
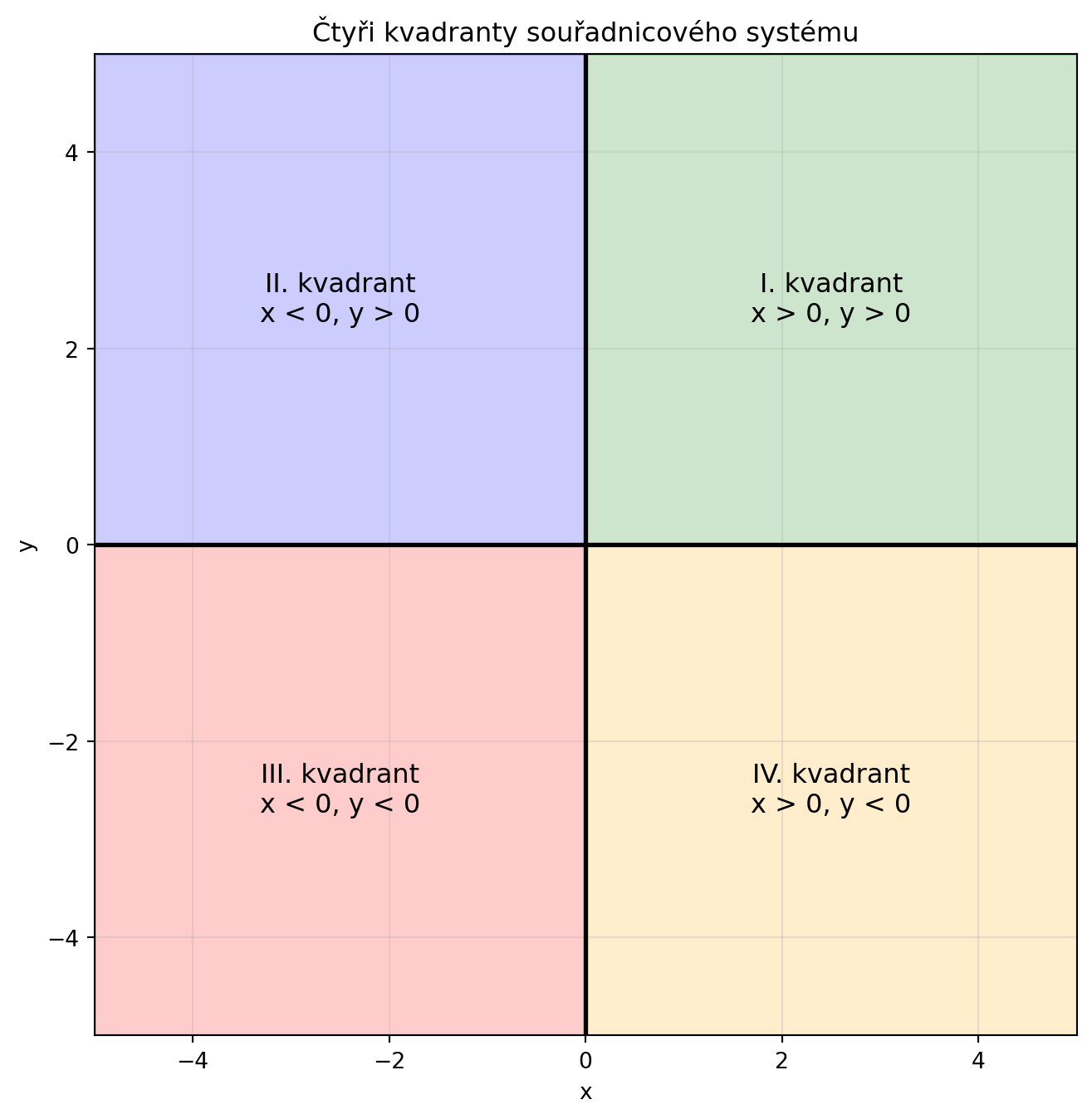
### Čtyři kvadranty
Rovina je rozdělena na čtyři části zvané **kvadranty**:
```{python}
#| fig-cap: "Čtyři kvadranty"
#| code-fold: true
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 8))
# Barevné vyplnění kvadrantů
ax.fill([0, 5, 5, 0], [0, 0, 5, 5], alpha=0.2, color='green')
ax.fill([-5, 0, 0, -5], [0, 0, 5, 5], alpha=0.2, color='blue')
ax.fill([-5, 0, 0, -5], [-5, -5, 0, 0], alpha=0.2, color='red')
ax.fill([0, 5, 5, 0], [-5, -5, 0, 0], alpha=0.2, color='orange')
# Osy
ax.axhline(y=0, color='k', linewidth=2)
ax.axvline(x=0, color='k', linewidth=2)
# Popisky kvadrantů
ax.text(2.5, 2.5, 'I. kvadrant\nx > 0, y > 0', ha='center', va='center', fontsize=12)
ax.text(-2.5, 2.5, 'II. kvadrant\nx < 0, y > 0', ha='center', va='center', fontsize=12)
ax.text(-2.5, -2.5, 'III. kvadrant\nx < 0, y < 0', ha='center', va='center', fontsize=12)
ax.text(2.5, -2.5, 'IV. kvadrant\nx > 0, y < 0', ha='center', va='center', fontsize=12)
ax.set_xlim(-5, 5)
ax.set_ylim(-5, 5)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Čtyři kvadranty souřadnicového systému')
plt.show()
```
| Kvadrant | x | y |
|----------|---|---|
| I. | + | + |
| II. | - | + |
| III. | - | - |
| IV. | + | - |
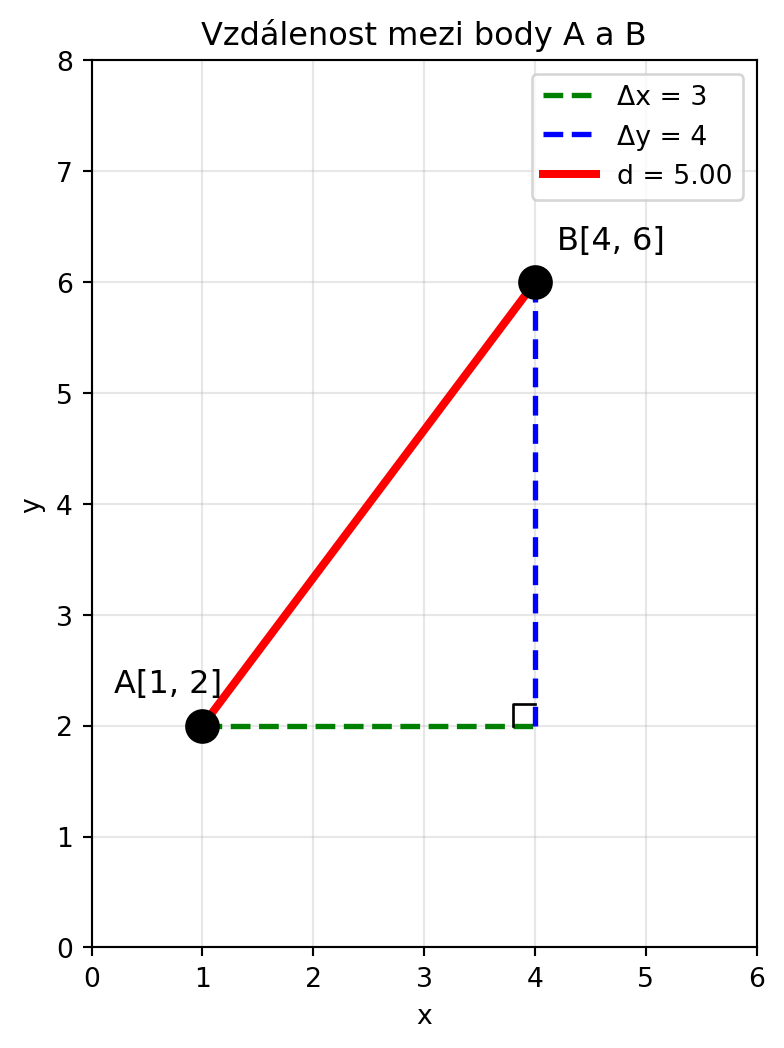
## Vzdálenost mezi dvěma body
Jak zjistíme vzdálenost mezi body A[x₁, y₁] a B[x₂, y₂]?
Použijeme **Pythagorovu větu**! Vzdálenost je přepona pravoúhlého trojúhelníku:
$$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$
```{python}
#| fig-cap: "Vzdálenost mezi dvěma body"
#| code-fold: true
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 6))
# Body
A = (1, 2)
B = (4, 6)
# Vzdálenost
dx = B[0] - A[0]
dy = B[1] - A[1]
d = np.sqrt(dx**2 + dy**2)
# Trojúhelník
ax.plot([A[0], B[0]], [A[1], A[1]], 'g--', linewidth=2, label=f'Δx = {dx}')
ax.plot([B[0], B[0]], [A[1], B[1]], 'b--', linewidth=2, label=f'Δy = {dy}')
ax.plot([A[0], B[0]], [A[1], B[1]], 'r-', linewidth=3, label=f'd = {d:.2f}')
# Body
ax.plot(*A, 'ko', markersize=12)
ax.plot(*B, 'ko', markersize=12)
ax.annotate('A[1, 2]', xy=A, xytext=(A[0]-0.8, A[1]+0.3), fontsize=12)
ax.annotate('B[4, 6]', xy=B, xytext=(B[0]+0.2, B[1]+0.3), fontsize=12)
# Pravý úhel
ax.plot([B[0]-0.2, B[0]-0.2, B[0]], [A[1], A[1]+0.2, A[1]+0.2], 'k-', linewidth=1)
ax.set_xlim(0, 6)
ax.set_ylim(0, 8)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.legend()
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Vzdálenost mezi body A a B')
plt.show()
```
::: {.callout-note title="Příklad"}
Vypočítejme vzdálenost mezi body A[1, 2] a B[4, 6]:
$$d = \sqrt{(4-1)^2 + (6-2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$$
:::
## Python: Práce se souřadnicemi
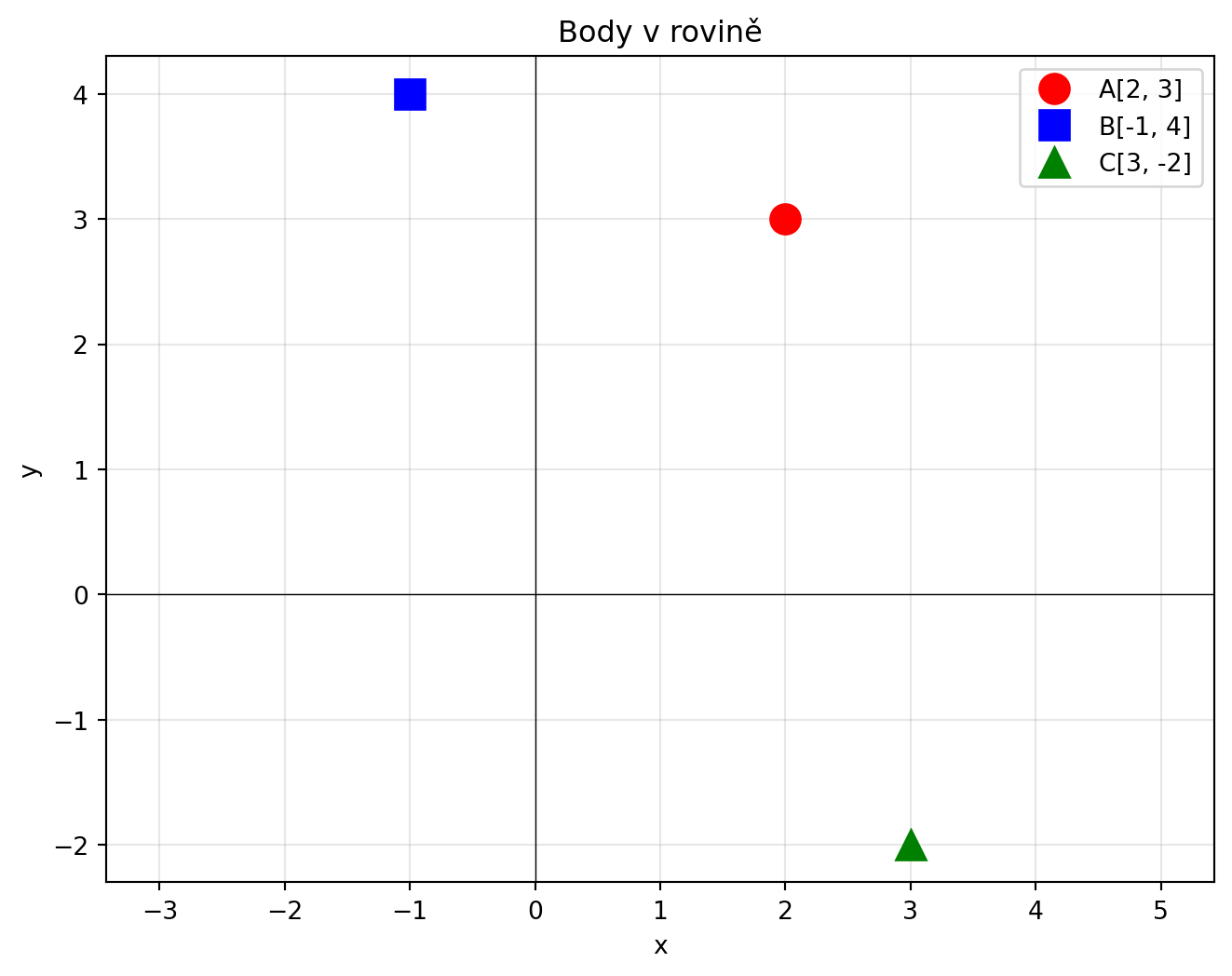
### Kreslení bodů
```{python}
#| fig-cap: "Body v Pythonu"
import matplotlib.pyplot as plt
# Definujeme body jako dvojice [x, y]
bod_A = [2, 3]
bod_B = [-1, 4]
bod_C = [3, -2]
# Nakreslíme je
plt.figure(figsize=(8, 6))
plt.plot(bod_A[0], bod_A[1], 'ro', markersize=12, label='A[2, 3]')
plt.plot(bod_B[0], bod_B[1], 'bs', markersize=12, label='B[-1, 4]')
plt.plot(bod_C[0], bod_C[1], 'g^', markersize=12, label='C[3, -2]')
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.title('Body v rovině')
plt.axis('equal')
plt.show()
```
### Výpočet vzdálenosti
```{python}
import numpy as np
def vzdalenost(bod1, bod2):
"""Vypočítá vzdálenost mezi dvěma body."""
x1, y1 = bod1
x2, y2 = bod2
return np.sqrt((x2 - x1)**2 + (y2 - y1)**2)
# Příklad
A = [1, 2]
B = [4, 6]
d = vzdalenost(A, B)
print(f"Vzdálenost mezi A a B: {d}")
```
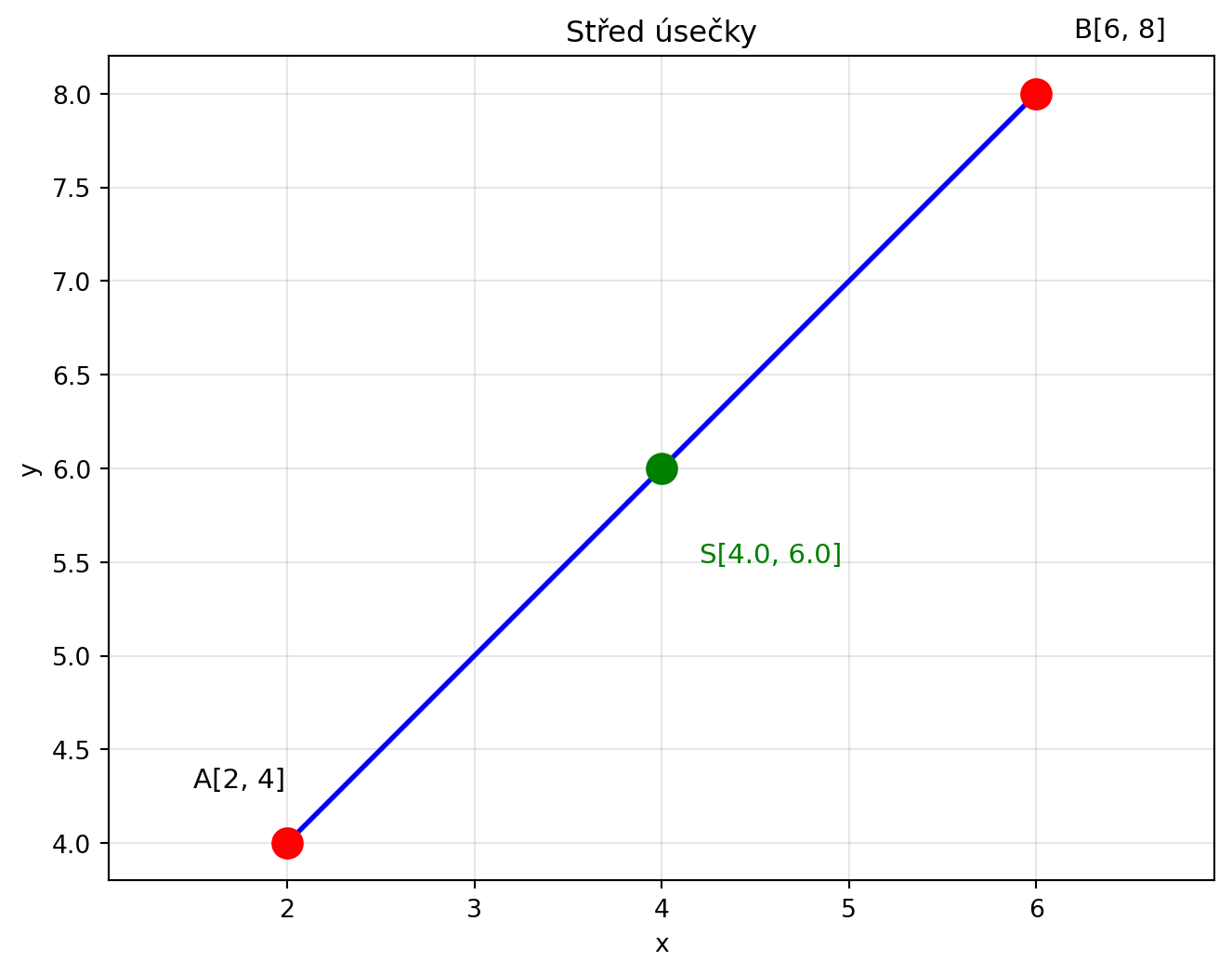
### Střed úsečky
Střed úsečky AB je bod, jehož souřadnice jsou průměry souřadnic krajních bodů:
$$S = \left[\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right]$$
```{python}
def stred_usecky(bod1, bod2):
"""Vypočítá střed úsečky."""
x1, y1 = bod1
x2, y2 = bod2
return [(x1 + x2) / 2, (y1 + y2) / 2]
A = [2, 4]
B = [6, 8]
S = stred_usecky(A, B)
print(f"Střed úsečky AB: {S}")
```
```{python}
#| fig-cap: "Střed úsečky"
# Vizualizace
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 6))
# Body a úsečka
A = [2, 4]
B = [6, 8]
S = stred_usecky(A, B)
plt.plot([A[0], B[0]], [A[1], B[1]], 'b-', linewidth=2)
plt.plot(A[0], A[1], 'ro', markersize=12)
plt.plot(B[0], B[1], 'ro', markersize=12)
plt.plot(S[0], S[1], 'go', markersize=12)
plt.annotate('A[2, 4]', xy=A, xytext=(A[0]-0.5, A[1]+0.3), fontsize=11)
plt.annotate('B[6, 8]', xy=B, xytext=(B[0]+0.2, B[1]+0.3), fontsize=11)
plt.annotate(f'S[{S[0]}, {S[1]}]', xy=S, xytext=(S[0]+0.2, S[1]-0.5), fontsize=11, color='green')
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Střed úsečky')
plt.axis('equal')
plt.show()
```
---
## Aplikace v praxi
### Souřadnice pixelů
Na obrazovce počítače má každý pixel své souřadnice. Pozor -- počítačová grafika má často **osu y obrácenou** (roste směrem dolů)!
```{python}
#| fig-cap: "Souřadnice pixelů (obrácená osa y)"
# Simulace pixelové mřížky
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 6))
# Mřížka pixelů
for i in range(10):
ax.axhline(y=i, color='gray', linewidth=0.5)
ax.axvline(x=i, color='gray', linewidth=0.5)
# Ukázkové pixely
pixely = [(2, 1), (5, 3), (7, 7)]
for px, py in pixely:
ax.add_patch(plt.Rectangle((px, py), 1, 1, color='blue', alpha=0.5))
ax.text(px+0.5, py+0.5, f'[{px},{py}]', ha='center', va='center', fontsize=9)
ax.set_xlim(0, 10)
ax.set_ylim(0, 10)
ax.invert_yaxis() # Obrátíme osu y
ax.set_xlabel('x (sloupec)')
ax.set_ylabel('y (řádek)')
ax.set_title('Souřadnice pixelů (y roste dolů)')
ax.set_aspect('equal')
plt.show()
```
### GPS souřadnice
GPS pozice se udává jako zeměpisná šířka (latitude) a délka (longitude):
```{python}
# Praha - Staroměstské náměstí
praha = {'lat': 50.0875, 'lon': 14.4214}
# Brno - náměstí Svobody
brno = {'lat': 49.1951, 'lon': 16.6068}
print(f"Praha: {praha['lat']}° N, {praha['lon']}° E")
print(f"Brno: {brno['lat']}° N, {brno['lon']}° E")
```
---
## Řešené příklady
### Příklad 1: Určení kvadrantu
V jakém kvadrantu leží bod P[-3, 5]?
**Řešení:**
- x = -3 (záporné, tedy vlevo od osy y)
- y = 5 (kladné, tedy nad osou x)
- Bod leží ve **II. kvadrantu**
```{python}
def urcit_kvadrant(x, y):
if x > 0 and y > 0:
return "I. kvadrant"
elif x < 0 and y > 0:
return "II. kvadrant"
elif x < 0 and y < 0:
return "III. kvadrant"
elif x > 0 and y < 0:
return "IV. kvadrant"
else:
return "Na ose"
print(urcit_kvadrant(-3, 5))
```
### Příklad 2: Vzdálenost od počátku
Jaká je vzdálenost bodu A[3, 4] od počátku [0, 0]?
**Řešení:**
$$d = \sqrt{(3-0)^2 + (4-0)^2} = \sqrt{9 + 16} = \sqrt{25} = 5$$
```{python}
A = [3, 4]
pocatek = [0, 0]
d = vzdalenost(A, pocatek)
print(f"Vzdálenost od počátku: {d}")
```
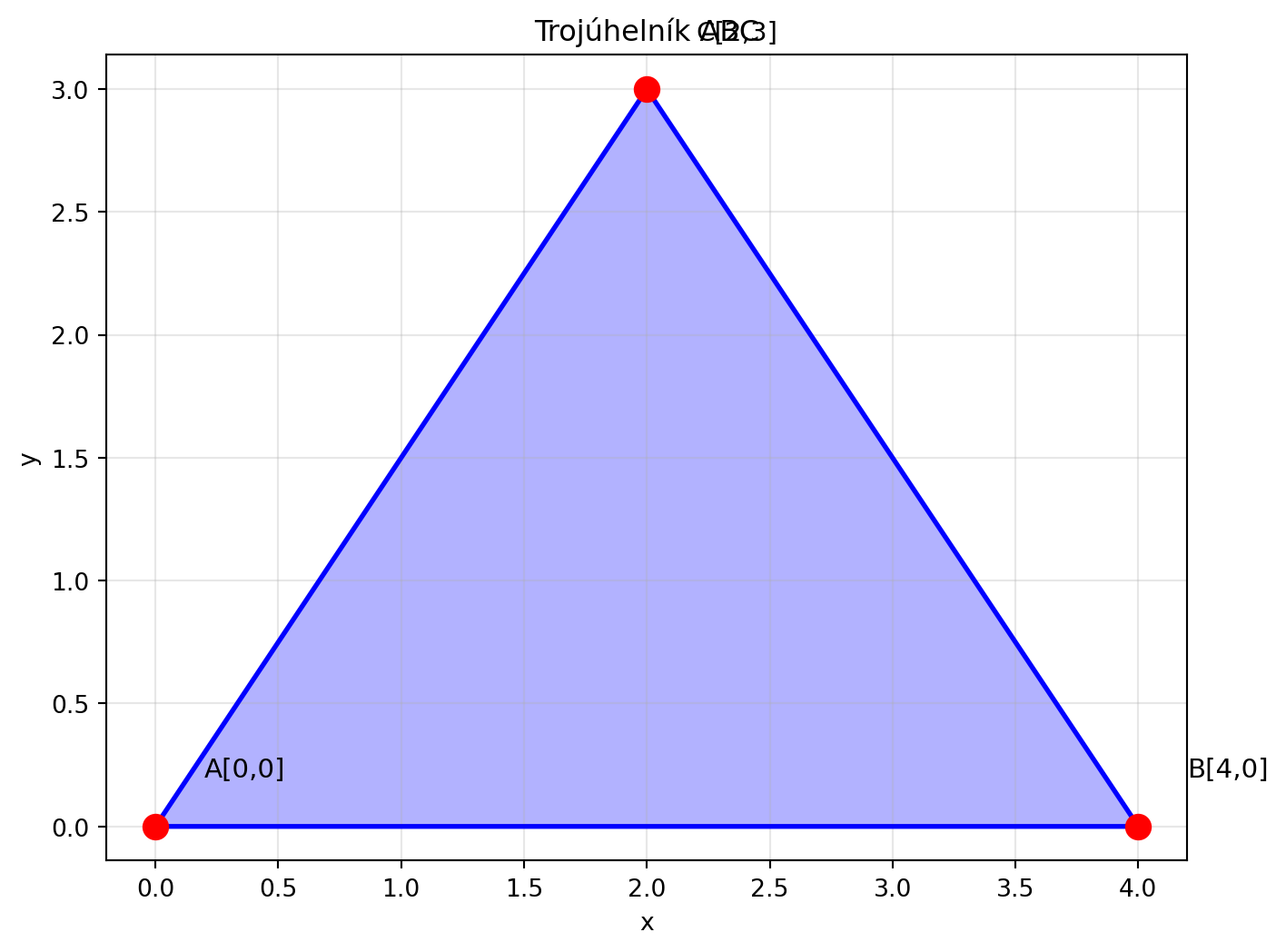
### Příklad 3: Trojúhelník
Jsou dány vrcholy trojúhelníku: A[0, 0], B[4, 0], C[2, 3]. Vypočítejte obvod trojúhelníku.
```{python}
A = [0, 0]
B = [4, 0]
C = [2, 3]
# Délky stran
AB = vzdalenost(A, B)
BC = vzdalenost(B, C)
CA = vzdalenost(C, A)
print(f"Strana AB: {AB:.2f}")
print(f"Strana BC: {BC:.2f}")
print(f"Strana CA: {CA:.2f}")
print(f"Obvod: {AB + BC + CA:.2f}")
```
```{python}
#| fig-cap: "Trojúhelník ABC"
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 6))
# Vrcholy
trojuhelnik_x = [A[0], B[0], C[0], A[0]] # Zavřeme trojúhelník
trojuhelnik_y = [A[1], B[1], C[1], A[1]]
plt.fill(trojuhelnik_x, trojuhelnik_y, alpha=0.3, color='blue')
plt.plot(trojuhelnik_x, trojuhelnik_y, 'b-', linewidth=2)
# Popisky vrcholů
for bod, nazev in [(A, 'A[0,0]'), (B, 'B[4,0]'), (C, 'C[2,3]')]:
plt.plot(bod[0], bod[1], 'ro', markersize=10)
plt.annotate(nazev, xy=bod, xytext=(bod[0]+0.2, bod[1]+0.2), fontsize=11)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Trojúhelník ABC')
plt.axis('equal')
plt.show()
```
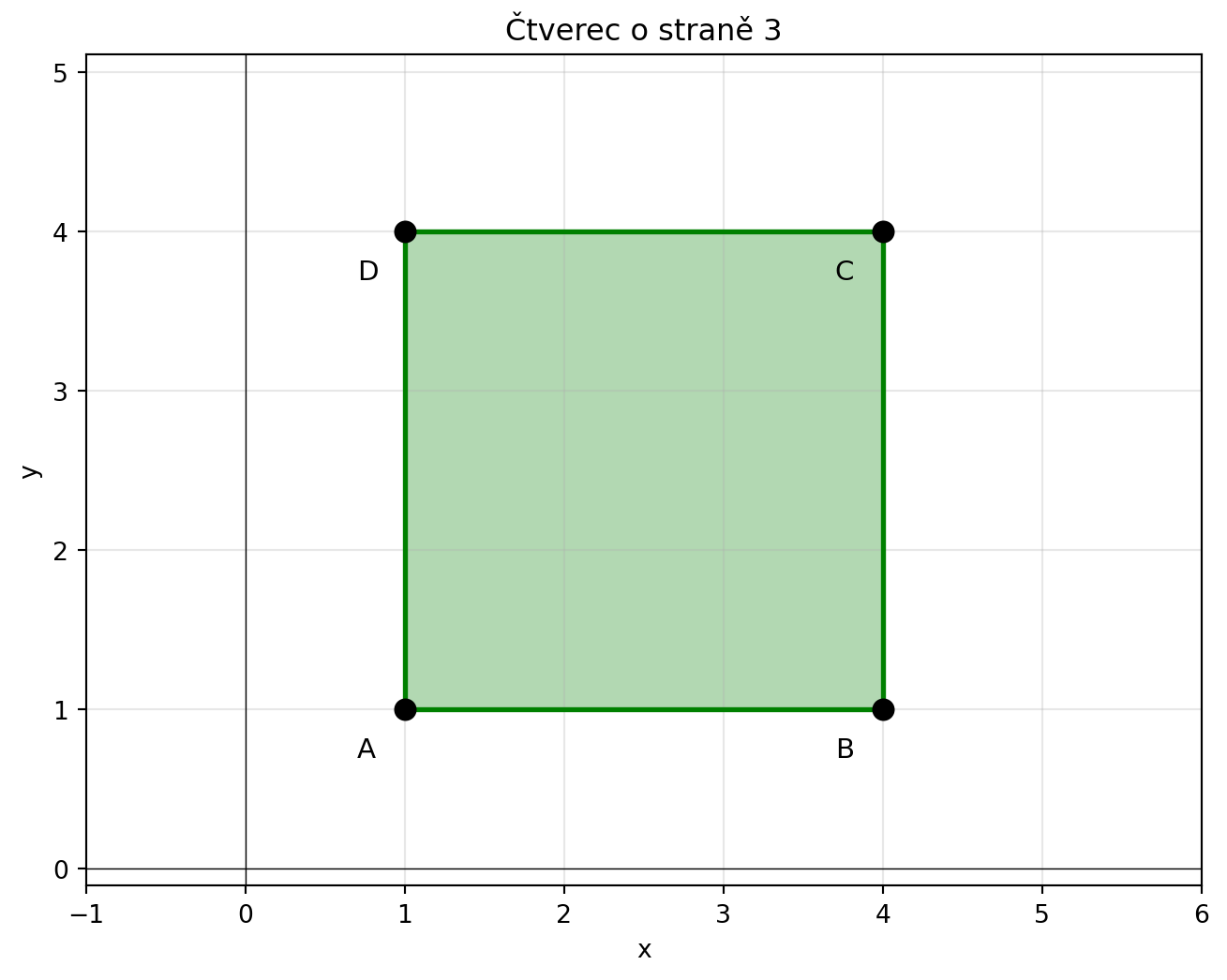
### Příklad 4: Čtverec
Nakreslete čtverec o straně 3 s levým dolním rohem v bodě [1, 1].
```{python}
#| fig-cap: "Čtverec"
# Vrcholy čtverce
import matplotlib.pyplot as plt
A = [1, 1]
B = [4, 1] # A + [3, 0]
C = [4, 4] # A + [3, 3]
D = [1, 4] # A + [0, 3]
plt.figure(figsize=(8, 6))
# Čtverec
ctverec_x = [A[0], B[0], C[0], D[0], A[0]]
ctverec_y = [A[1], B[1], C[1], D[1], A[1]]
plt.fill(ctverec_x, ctverec_y, alpha=0.3, color='green')
plt.plot(ctverec_x, ctverec_y, 'g-', linewidth=2)
# Vrcholy
for bod, nazev in [(A, 'A'), (B, 'B'), (C, 'C'), (D, 'D')]:
plt.plot(bod[0], bod[1], 'ko', markersize=8)
plt.annotate(nazev, xy=bod, xytext=(bod[0]-0.3, bod[1]-0.3), fontsize=11)
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Čtverec o straně 3')
plt.axis('equal')
plt.xlim(-1, 6)
plt.ylim(-1, 6)
plt.show()
```
---
## Cvičení
::: {.callout-warning title="Cvičení 1: Nakresli body"}
Nakreslete body A[2, 3], B[-4, 1], C[0, -2], D[3, -4] do souřadnicového systému a určete, ve kterém kvadrantu leží.
<details>
<summary>Řešení</summary>
- A[2, 3]: I. kvadrant (x > 0, y > 0)
- B[-4, 1]: II. kvadrant (x < 0, y > 0)
- C[0, -2]: na ose y (x = 0)
- D[3, -4]: IV. kvadrant (x > 0, y < 0)
</details>
:::
::: {.callout-warning title="Cvičení 2: Vzdálenost"}
Vypočítejte vzdálenost mezi body P[1, 1] a Q[4, 5].
**Výsledek:** 5
<details>
<summary>Řešení</summary>
$d = \sqrt{(4-1)^2 + (5-1)^2} = \sqrt{9 + 16} = \sqrt{25} = 5$
</details>
:::
::: {.callout-warning title="Cvičení 3: Střed úsečky"}
Najděte střed úsečky s krajními body A[-2, 4] a B[6, 0].
**Výsledek:** S[2, 2]
<details>
<summary>Řešení</summary>
$S_x = \frac{-2 + 6}{2} = 2$
$S_y = \frac{4 + 0}{2} = 2$
Střed je S[2, 2]
</details>
:::
::: {.callout-warning title="Cvičení 4: Obdélník"}
Jsou dány dva protilehlé vrcholy obdélníku: A[1, 2] a C[5, 6]. Najděte zbývající dva vrcholy B a D (předpokládejte, že strany jsou rovnoběžné s osami).
<details>
<summary>Řešení</summary>
B[5, 2] a D[1, 6]
</details>
:::
::: {.callout-warning title="Cvičení 5: Rovnostranný trojúhelník"}
Napište Python funkci, která pro danou stranu `a` a bod `A` (levý dolní vrchol) vypočítá souřadnice všech tří vrcholů rovnostranného trojúhelníku.
<details>
<summary>Nápověda</summary>
Výška rovnostranného trojúhelníku je $h = \frac{a \cdot \sqrt{3}}{2}$
</details>
<details>
<summary>Řešení</summary>
```python
import numpy as np
def rovnostranny_trojuhelnik(A, a):
"""Vrátí vrcholy rovnostranného trojúhelníku."""
B = [A[0] + a, A[1]]
vyska = a * np.sqrt(3) / 2
C = [A[0] + a/2, A[1] + vyska]
return A, B, C
A = [0, 0]
a = 4
vrcholy = rovnostranny_trojuhelnik(A, a)
print(vrcholy)
```
</details>
:::
::: {.callout-warning title="Cvičení 6: Vzdálenost od přímky"}
Bod P[3, 4] leží na kružnici se středem v počátku. Jaký je poloměr této kružnice?
**Výsledek:** r = 5
<details>
<summary>Řešení</summary>
Poloměr je vzdálenost od středu: $r = \sqrt{3^2 + 4^2} = 5$
</details>
:::
---
## Shrnutí
::: {.callout-note title="Co si zapamatovat"}
- **Kartézská soustava souřadnic** má dvě osy: x (vodorovná) a y (svislá)
- Bod zapisujeme jako **[x, y]**
- Rovina je rozdělena do **čtyř kvadrantů**
- **Vzdálenost** mezi body: $d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
- **Střed úsečky**: $S = \left[\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right]$
- V Pythonu body reprezentujeme jako seznamy `[x, y]` nebo n-tice `(x, y)`
:::
V další kapitole se naučíme, co je funkce -- základní koncept, který spojuje vstupy s výstupy a je klíčový pro pochopení neuronových sítí.