import numpy as np
import matplotlib.pyplot as plt
u = np.array([2, 1])
v = np.array([1, 3])
soucet = u + v
print(f"u = {u}")
print(f"v = {v}")
print(f"u + v = {soucet}")u = [2 1]
v = [1 3]
u + v = [3 4]V této kapitole se naučíte:
Vektory sčítáme po složkách:
\[\mathbf{u} + \mathbf{v} = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} + \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \begin{bmatrix} u_1 + v_1 \\ u_2 + v_2 \end{bmatrix}\]
import numpy as np
import matplotlib.pyplot as plt
u = np.array([2, 1])
v = np.array([1, 3])
soucet = u + v
print(f"u = {u}")
print(f"v = {v}")
print(f"u + v = {soucet}")u = [2 1]
v = [1 3]
u + v = [3 4]Sčítání vektorů si představíme jako “jdi podle u, pak podle v”:
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10, 8))
u = np.array([3, 1])
v = np.array([1, 2])
soucet = u + v
# Vektor u z počátku
ax.annotate('', xy=u, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='blue', lw=2))
ax.text(u[0]/2 - 0.3, u[1]/2 + 0.2, 'u', fontsize=14, color='blue')
# Vektor v z počátku
ax.annotate('', xy=v, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='red', lw=2))
ax.text(v[0]/2 + 0.2, v[1]/2, 'v', fontsize=14, color='red')
# Vektor v posunutý za u
ax.annotate('', xy=soucet, xytext=u,
arrowprops=dict(arrowstyle='->', color='red', lw=2, linestyle='--'))
# Vektor u posunutý za v
ax.annotate('', xy=soucet, xytext=v,
arrowprops=dict(arrowstyle='->', color='blue', lw=2, linestyle='--'))
# Součet
ax.annotate('', xy=soucet, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='green', lw=3))
ax.text(soucet[0]/2 + 0.2, soucet[1]/2, 'u + v', fontsize=14, color='green')
ax.plot(*soucet, 'go', markersize=10)
ax.text(soucet[0] + 0.15, soucet[1] + 0.15, f'{list(soucet)}', fontsize=11)
ax.set_xlim(-0.5, 5)
ax.set_ylim(-0.5, 4)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='k', linewidth=0.5)
ax.axvline(x=0, color='k', linewidth=0.5)
ax.set_title('Sčítání vektorů: pravidlo rovnoběžníku')
plt.show()
Odčítání funguje podobně:
\[\mathbf{u} - \mathbf{v} = \begin{bmatrix} u_1 - v_1 \\ u_2 - v_2 \end{bmatrix}\]
import numpy as np
u = np.array([4, 3])
v = np.array([1, 2])
rozdil = u - v
print(f"u = {u}")
print(f"v = {v}")
print(f"u - v = {rozdil}")u = [4 3]
v = [1 2]
u - v = [3 1]Vektor z bodu A do bodu B je: \[\overrightarrow{AB} = \mathbf{B} - \mathbf{A}\]
import numpy as np
import matplotlib.pyplot as plt
A = np.array([1, 2])
B = np.array([4, 5])
AB = B - A
fig, ax = plt.subplots(figsize=(8, 6))
# Body
ax.plot(*A, 'bo', markersize=12)
ax.plot(*B, 'ro', markersize=12)
ax.text(A[0]-0.3, A[1]+0.2, f'A{list(A)}', fontsize=11, color='blue')
ax.text(B[0]+0.1, B[1]+0.2, f'B{list(B)}', fontsize=11, color='red')
# Vektor AB
ax.annotate('', xy=B, xytext=A,
arrowprops=dict(arrowstyle='->', color='green', lw=2))
ax.text((A[0]+B[0])/2 + 0.2, (A[1]+B[1])/2, f'AB = {list(AB)}',
fontsize=11, color='green')
ax.set_xlim(0, 6)
ax.set_ylim(0, 7)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.set_title('Vektor AB = B - A')
plt.show()
print(f"A = {A}")
print(f"B = {B}")
print(f"Vektor AB = B - A = {AB}")
A = [1 2]
B = [4 5]
Vektor AB = B - A = [3 3]Vektor vynásobíme číslem (skalárem) tak, že vynásobíme každou složku:
\[c \cdot \mathbf{v} = c \cdot \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \begin{bmatrix} c \cdot v_1 \\ c \cdot v_2 \end{bmatrix}\]
import numpy as np
v = np.array([2, 1])
print(f"v = {v}")
print(f"2 * v = {2 * v}")
print(f"0.5 * v = {0.5 * v}")
print(f"-1 * v = {-1 * v}")v = [2 1]
2 * v = [4 2]
0.5 * v = [1. 0.5]
-1 * v = [-2 -1]import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10, 6))
v = np.array([2, 1])
# Původní vektor
ax.annotate('', xy=v, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='blue', lw=2))
ax.text(v[0]+0.1, v[1]+0.1, 'v', fontsize=12, color='blue')
# 2 * v
v2 = 2 * v
ax.annotate('', xy=v2, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='green', lw=2))
ax.text(v2[0]+0.1, v2[1]+0.1, '2v', fontsize=12, color='green')
# 0.5 * v
v05 = 0.5 * v
ax.annotate('', xy=v05, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='orange', lw=2))
ax.text(v05[0]+0.1, v05[1]+0.1, '0.5v', fontsize=12, color='orange')
# -1 * v
vm1 = -1 * v
ax.annotate('', xy=vm1, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='red', lw=2))
ax.text(vm1[0]-0.5, vm1[1], '-v', fontsize=12, color='red')
ax.set_xlim(-3, 5)
ax.set_ylim(-2, 3)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='k', linewidth=0.5)
ax.axvline(x=0, color='k', linewidth=0.5)
ax.set_title('Násobení vektoru skalárem mění jeho délku (a směr pro záporné c)')
plt.show()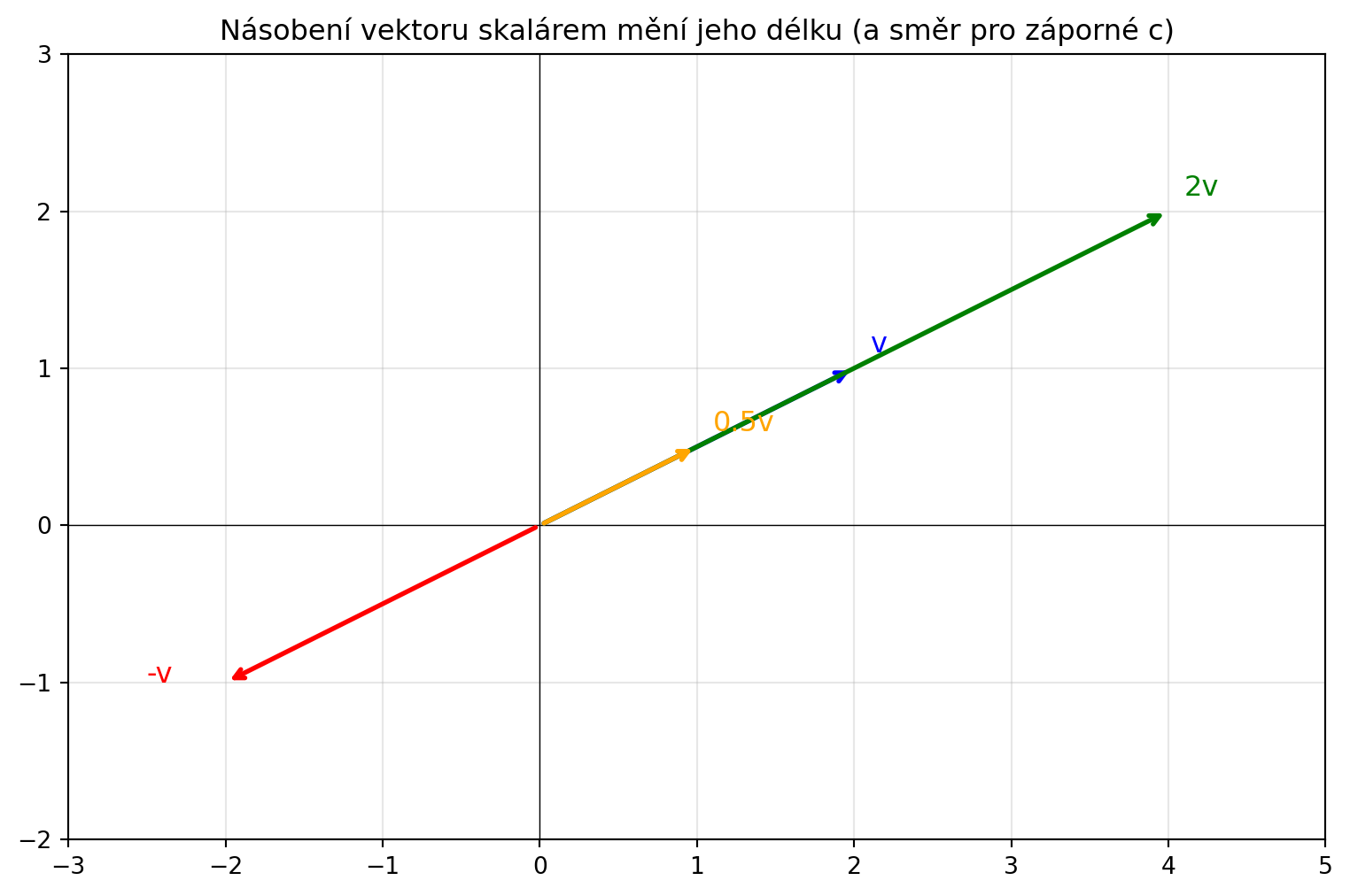
Skalární součin je jedna z nejdůležitějších operací s vektory. Výsledkem je číslo (skalár), ne vektor.
\[\mathbf{u} \cdot \mathbf{v} = u_1 v_1 + u_2 v_2 + ... + u_n v_n = \sum_{i=1}^{n} u_i v_i\]
import numpy as np
u = np.array([1, 2, 3])
v = np.array([4, 5, 6])
# Ručně
dot_rucne = u[0]*v[0] + u[1]*v[1] + u[2]*v[2]
print(f"u · v = 1·4 + 2·5 + 3·6 = 4 + 10 + 18 = {dot_rucne}")
# NumPy způsoby
dot_numpy = np.dot(u, v)
dot_at = u @ v # Operátor @
print(f"np.dot(u, v) = {dot_numpy}")
print(f"u @ v = {dot_at}")u · v = 1·4 + 2·5 + 3·6 = 4 + 10 + 18 = 32
np.dot(u, v) = 32
u @ v = 32Skalární součin lze vyjádřit také pomocí úhlu:
\[\mathbf{u} \cdot \mathbf{v} = \|\mathbf{u}\| \cdot \|\mathbf{v}\| \cdot \cos(\theta)\]
kde \(\theta\) je úhel mezi vektory.
import numpy as np
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
vektory = [
(np.array([2, 0]), np.array([1, 1.5]), "Ostrý úhel: u·v > 0"),
(np.array([2, 0]), np.array([0, 2]), "Pravý úhel: u·v = 0"),
(np.array([2, 0]), np.array([-1, 1]), "Tupý úhel: u·v < 0")
]
for ax, (u, v, titulek) in zip(axes, vektory):
ax.annotate('', xy=u, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='blue', lw=2))
ax.annotate('', xy=v, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='red', lw=2))
ax.text(u[0]+0.1, u[1]+0.1, 'u', color='blue', fontsize=12)
ax.text(v[0]+0.1, v[1]+0.1, 'v', color='red', fontsize=12)
dot = np.dot(u, v)
ax.set_title(f'{titulek}\nu·v = {dot:.1f}', fontsize=11)
ax.set_xlim(-2, 3)
ax.set_ylim(-0.5, 2.5)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='k', linewidth=0.5)
ax.axvline(x=0, color='k', linewidth=0.5)
plt.tight_layout()
plt.show()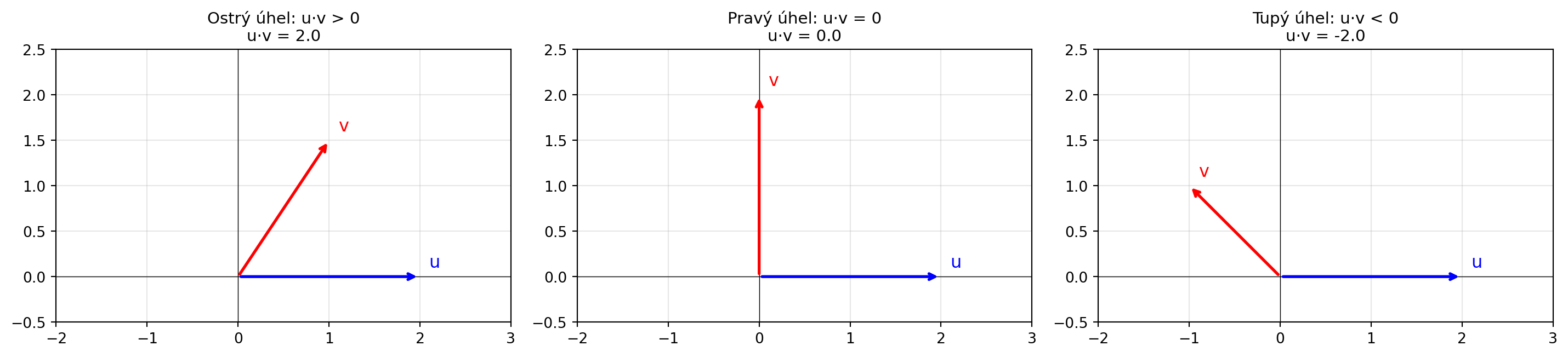
| Hodnota u·v | Úhel θ | Vztah vektorů |
|---|---|---|
| > 0 | 0° < θ < 90° | Podobný směr |
| = 0 | θ = 90° | Kolmé (ortogonální) |
| < 0 | 90° < θ < 180° | Opačný směr |
import numpy as np
def uhel_mezi_vektory(u, v):
"""Vypočítá úhel mezi dvěma vektory v radiánech a stupních."""
cos_uhel = np.dot(u, v) / (np.linalg.norm(u) * np.linalg.norm(v))
# Ošetříme numerické chyby (cos musí být v [-1, 1])
cos_uhel = np.clip(cos_uhel, -1, 1)
uhel_rad = np.arccos(cos_uhel)
uhel_deg = np.degrees(uhel_rad)
return uhel_rad, uhel_deg
# Příklady
u = np.array([1, 0])
v = np.array([1, 1])
rad, deg = uhel_mezi_vektory(u, v)
print(f"Úhel mezi [1,0] a [1,1]: {deg:.1f}°")
# Kolmé vektory
u2 = np.array([1, 0])
v2 = np.array([0, 1])
rad2, deg2 = uhel_mezi_vektory(u2, v2)
print(f"Úhel mezi [1,0] a [0,1]: {deg2:.1f}°")Úhel mezi [1,0] a [1,1]: 45.0°
Úhel mezi [1,0] a [0,1]: 90.0°Kosínová podobnost měří, jak moc jsou dva vektory “podobné” bez ohledu na jejich délku:
\[\text{cos\_sim}(\mathbf{u}, \mathbf{v}) = \frac{\mathbf{u} \cdot \mathbf{v}}{\|\mathbf{u}\| \cdot \|\mathbf{v}\|} = \cos(\theta)\]
Hodnota je mezi -1 a 1:
import numpy as np
def kosinova_podobnost(u, v):
"""Vypočítá kosínovou podobnost dvou vektorů."""
return np.dot(u, v) / (np.linalg.norm(u) * np.linalg.norm(v))
# Příklady
a = np.array([1, 2, 3])
b = np.array([2, 4, 6]) # Stejný směr (b = 2*a)
c = np.array([1, 0, 0])
d = np.array([-1, -2, -3]) # Opačný směr
print(f"Podobnost a a b (stejný směr): {kosinova_podobnost(a, b):.3f}")
print(f"Podobnost a a c: {kosinova_podobnost(a, c):.3f}")
print(f"Podobnost a a d (opačný směr): {kosinova_podobnost(a, d):.3f}")Podobnost a a b (stejný směr): 1.000
Podobnost a a c: 0.267
Podobnost a a d (opačný směr): -1.000V NLP se kosínová podobnost používá pro měření podobnosti dokumentů nebo slov:
# Zjednodušené word embeddings
import numpy as np
slova = {
'pes': np.array([0.9, 0.1, 0.8]),
'kočka': np.array([0.8, 0.2, 0.7]),
'auto': np.array([0.1, 0.9, 0.2]),
'štěně': np.array([0.85, 0.15, 0.9])
}
print("Kosínová podobnost mezi slovy:")
print("-" * 35)
for s1 in slova:
for s2 in slova:
if s1 < s2: # Každou dvojici jen jednou
sim = kosinova_podobnost(slova[s1], slova[s2])
print(f"{s1:8} - {s2:8}: {sim:.3f}")Kosínová podobnost mezi slovy:
-----------------------------------
pes - štěně : 0.996
kočka - pes : 0.995
kočka - štěně : 0.993
auto - pes : 0.303
auto - kočka : 0.399
auto - štěně : 0.346import numpy as np
import matplotlib.pyplot as plt
nazvy = list(slova.keys())
n = len(nazvy)
matice = np.zeros((n, n))
for i, s1 in enumerate(nazvy):
for j, s2 in enumerate(nazvy):
matice[i, j] = kosinova_podobnost(slova[s1], slova[s2])
plt.figure(figsize=(8, 6))
plt.imshow(matice, cmap='RdYlGn', vmin=-1, vmax=1)
plt.colorbar(label='Kosínová podobnost')
plt.xticks(range(n), nazvy)
plt.yticks(range(n), nazvy)
plt.title('Matice podobnosti slov')
# Hodnoty do buněk
for i in range(n):
for j in range(n):
plt.text(j, i, f'{matice[i,j]:.2f}', ha='center', va='center')
plt.show()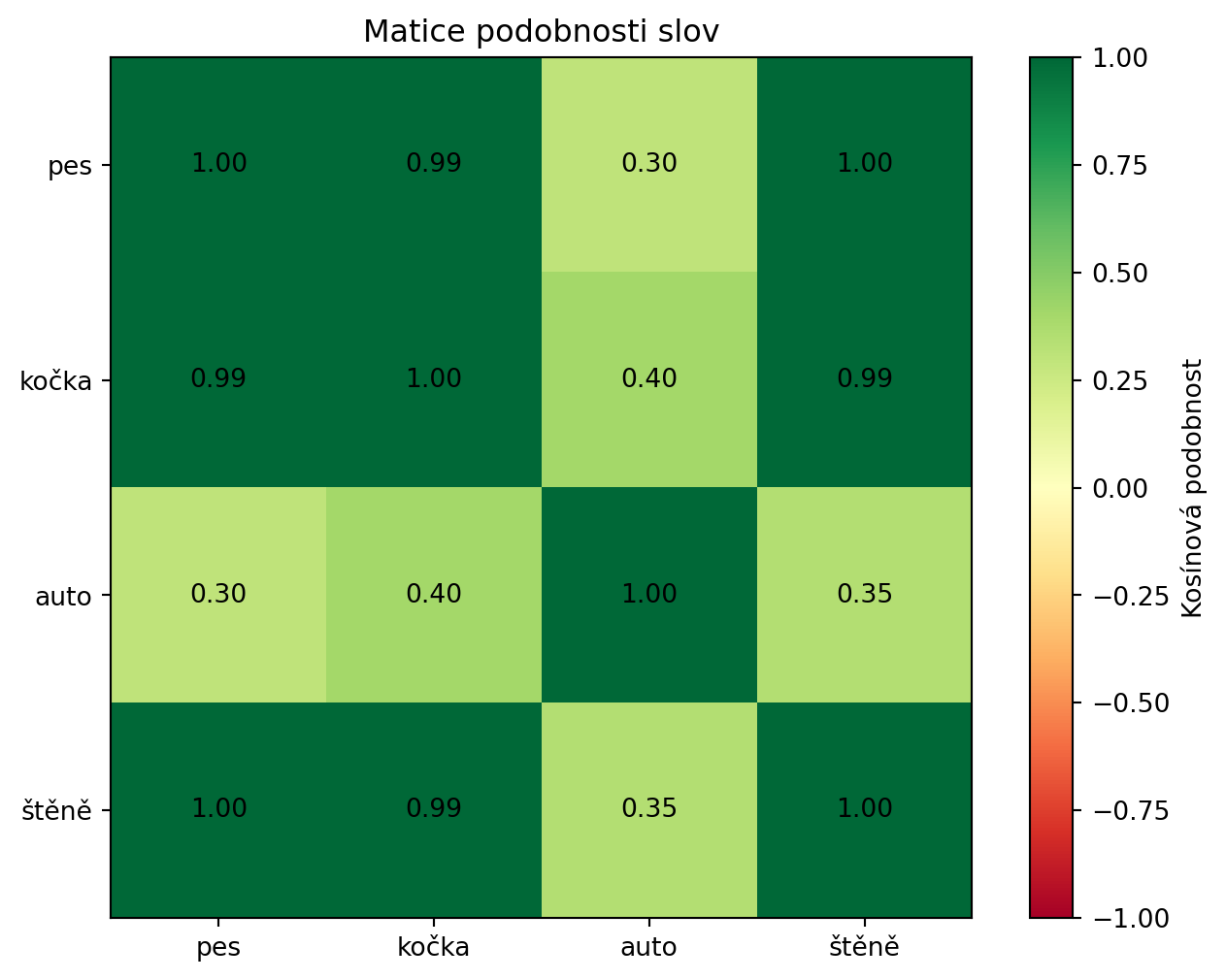
Projekce vektoru \(\mathbf{u}\) na vektor \(\mathbf{v}\) je “stín” vektoru u ve směru v:
\[\text{proj}_{\mathbf{v}}(\mathbf{u}) = \frac{\mathbf{u} \cdot \mathbf{v}}{\mathbf{v} \cdot \mathbf{v}} \cdot \mathbf{v}\]
import numpy as np
import matplotlib.pyplot as plt
u = np.array([3, 2])
v = np.array([4, 0])
# Projekce u na v
projekce = (np.dot(u, v) / np.dot(v, v)) * v
fig, ax = plt.subplots(figsize=(10, 6))
# Vektory
ax.annotate('', xy=u, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='blue', lw=2))
ax.annotate('', xy=v, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='green', lw=2))
ax.annotate('', xy=projekce, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='red', lw=3))
# Kolmice
ax.plot([u[0], projekce[0]], [u[1], projekce[1]], 'k--', linewidth=1)
ax.text(u[0]+0.1, u[1]+0.1, 'u', color='blue', fontsize=14)
ax.text(v[0]+0.1, v[1]+0.1, 'v', color='green', fontsize=14)
ax.text(projekce[0]/2, -0.4, 'proj_v(u)', color='red', fontsize=12)
ax.set_xlim(-0.5, 5)
ax.set_ylim(-1, 3)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='k', linewidth=0.5)
ax.axvline(x=0, color='k', linewidth=0.5)
ax.set_title('Projekce vektoru u na vektor v')
plt.show()
print(f"u = {u}")
print(f"v = {v}")
print(f"Projekce u na v = {projekce}")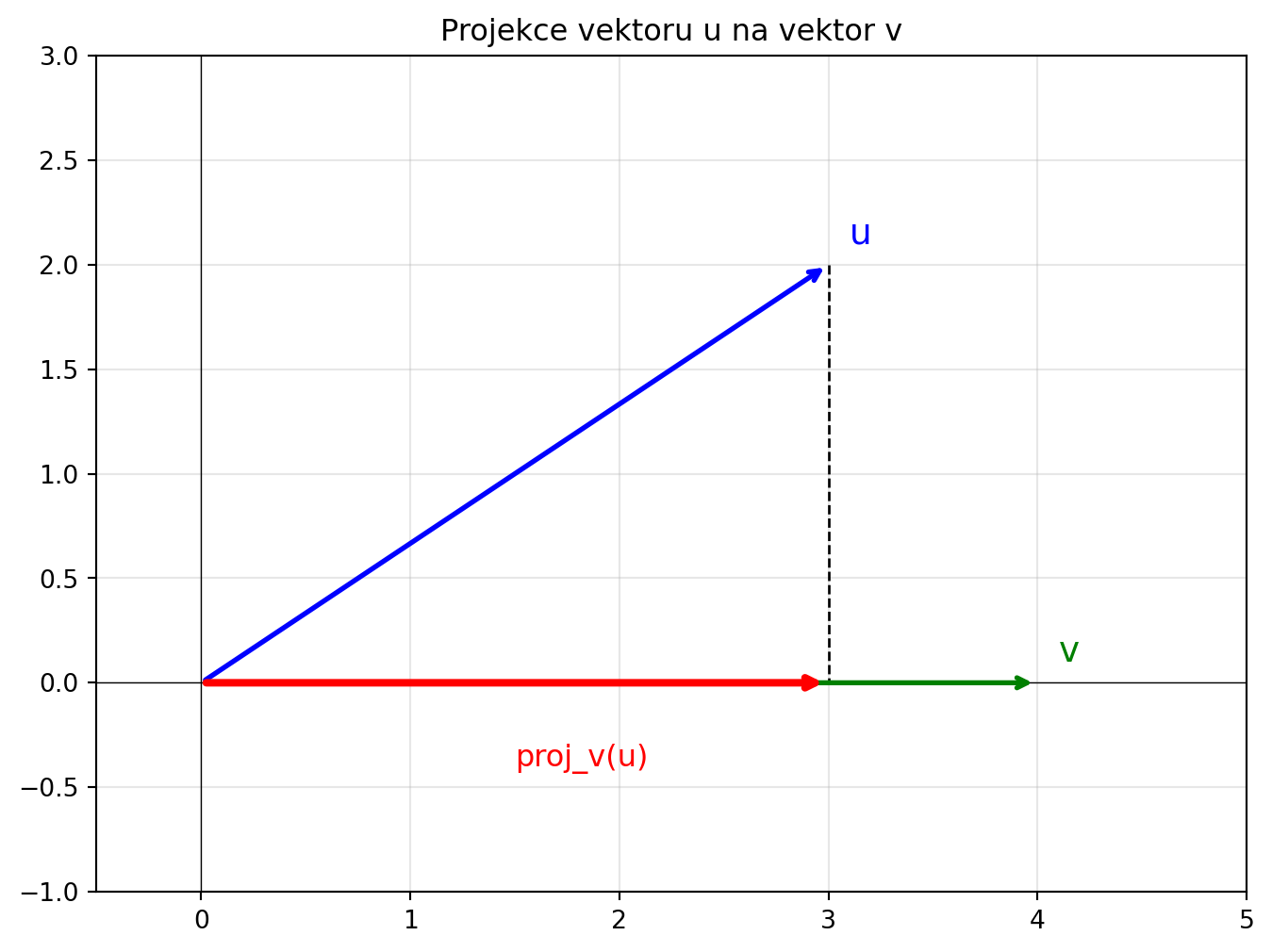
u = [3 2]
v = [4 0]
Projekce u na v = [3. 0.]# Vytvoření vektorů
import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print("Vektory:")
print(f" a = {a}")
print(f" b = {b}")
print("\nZákladní operace:")
print(f" a + b = {a + b}")
print(f" a - b = {a - b}")
print(f" 2 * a = {2 * a}")
print("\nPo-složkové operace:")
print(f" a * b = {a * b}") # Element-wise!
print(f" a / b = {np.round(a / b, 3)}")
print(f" a ** 2 = {a ** 2}")
print("\nSkalární součin:")
print(f" a · b = {np.dot(a, b)}")
print(f" a @ b = {a @ b}")
print("\nNormy:")
print(f" ||a|| = {np.linalg.norm(a):.3f}")
print("\nUžitečné funkce:")
print(f" sum(a) = {np.sum(a)}")
print(f" mean(a) = {np.mean(a)}")
print(f" max(a) = {np.max(a)}")Vektory:
a = [1 2 3]
b = [4 5 6]
Základní operace:
a + b = [5 7 9]
a - b = [-3 -3 -3]
2 * a = [2 4 6]
Po-složkové operace:
a * b = [ 4 10 18]
a / b = [0.25 0.4 0.5 ]
a ** 2 = [1 4 9]
Skalární součin:
a · b = 32
a @ b = 32
Normy:
||a|| = 3.742
Užitečné funkce:
sum(a) = 6
mean(a) = 2.0
max(a) = 3Jsou dány vektory \(\mathbf{u} = [3, -1, 2]\) a \(\mathbf{v} = [1, 4, -2]\). Vypočítejte \(\mathbf{u} + \mathbf{v}\) a \(\mathbf{u} - \mathbf{v}\).
import numpy as np
u = np.array([3, -1, 2])
v = np.array([1, 4, -2])
print(f"u + v = [{3+1}, {-1+4}, {2-2}] = {u + v}")
print(f"u - v = [{3-1}, {-1-4}, {2-(-2)}] = {u - v}")u + v = [4, 3, 0] = [4 3 0]
u - v = [2, -5, 4] = [ 2 -5 4]Vypočítejte skalární součin vektorů \(\mathbf{a} = [2, 3]\) a \(\mathbf{b} = [4, -1]\).
import numpy as np
a = np.array([2, 3])
b = np.array([4, -1])
dot = a @ b
print(f"a · b = 2·4 + 3·(-1) = 8 - 3 = {dot}")a · b = 2·4 + 3·(-1) = 8 - 3 = 5Jaký je úhel mezi vektory \(\mathbf{u} = [1, 1]\) a \(\mathbf{v} = [1, 0]\)?
import numpy as np
u = np.array([1, 1])
v = np.array([1, 0])
cos_theta = np.dot(u, v) / (np.linalg.norm(u) * np.linalg.norm(v))
theta = np.degrees(np.arccos(cos_theta))
print(f"cos(θ) = (1·1 + 1·0) / (√2 · 1) = 1/√2 ≈ {cos_theta:.4f}")
print(f"θ = {theta:.1f}°")cos(θ) = (1·1 + 1·0) / (√2 · 1) = 1/√2 ≈ 0.7071
θ = 45.0°Jsou vektory \(\mathbf{a} = [3, 4]\) a \(\mathbf{b} = [-4, 3]\) kolmé?
import numpy as np
a = np.array([3, 4])
b = np.array([-4, 3])
dot = a @ b
print(f"a · b = 3·(-4) + 4·3 = -12 + 12 = {dot}")
print(f"Vektory jsou {'kolmé' if dot == 0 else 'nekolmé'}")a · b = 3·(-4) + 4·3 = -12 + 12 = 0
Vektory jsou kolméVypočítejte kosínovou podobnost vektorů \(\mathbf{x} = [1, 2, 3]\) a \(\mathbf{y} = [4, 5, 6]\).
import numpy as np
x = np.array([1, 2, 3])
y = np.array([4, 5, 6])
sim = kosinova_podobnost(x, y)
print(f"x · y = {np.dot(x, y)}")
print(f"||x|| = {np.linalg.norm(x):.3f}")
print(f"||y|| = {np.linalg.norm(y):.3f}")
print(f"cos_sim = {np.dot(x,y)} / ({np.linalg.norm(x):.3f} · {np.linalg.norm(y):.3f}) = {sim:.4f}")x · y = 32
||x|| = 3.742
||y|| = 8.775
cos_sim = 32 / (3.742 · 8.775) = 0.9746Vypočítejte \([2, 5, -1] + [-1, 3, 4]\).
Výsledek: [1, 8, 3]
Vypočítejte \(3 \cdot [2, -1, 4]\).
Výsledek: [6, -3, 12]
Vypočítejte skalární součin \([1, 2, 3] \cdot [2, 0, -1]\).
Výsledek: -1
Pro jakou hodnotu \(k\) jsou vektory \([k, 2]\) a \([4, -6]\) kolmé?
Výsledek: k = 3
\(k·4 + 2·(-6) = 0\)
\(4k - 12 = 0\)
\(k = 3\)Jaký je úhel mezi vektory \([1, 0, 0]\) a \([0, 1, 0]\)?
Výsledek: 90°
Vypočítejte kosínovou podobnost vektorů \([3, 4]\) a \([6, 8]\).
Výsledek: 1.0 (stejný směr)
import numpy as np
u = np.array([3, 4])
v = np.array([6, 8]) # v = 2*u
sim = np.dot(u, v) / (np.linalg.norm(u) * np.linalg.norm(v))
# = 50 / (5 * 10) = 1.0+, -, * (po složkách), @ nebo np.dot() (skalární součin)V další kapitole přejdeme k maticím – “tabulkám čísel”, které jsou základem pro reprezentaci neuronových sítí.