# Nelineární funkce
::: {.callout-tip title="Co se naučíte"}
V této kapitole se naučíte:
- Co je kvadratická funkce a parabola
- Jak fungují mocninné funkce
- Principy exponenciálního růstu a poklesu
- Co je logaritmus a k čemu slouží
- Kde se tyto funkce používají v praxi a strojovém učení
:::
## Proč nelineární funkce?
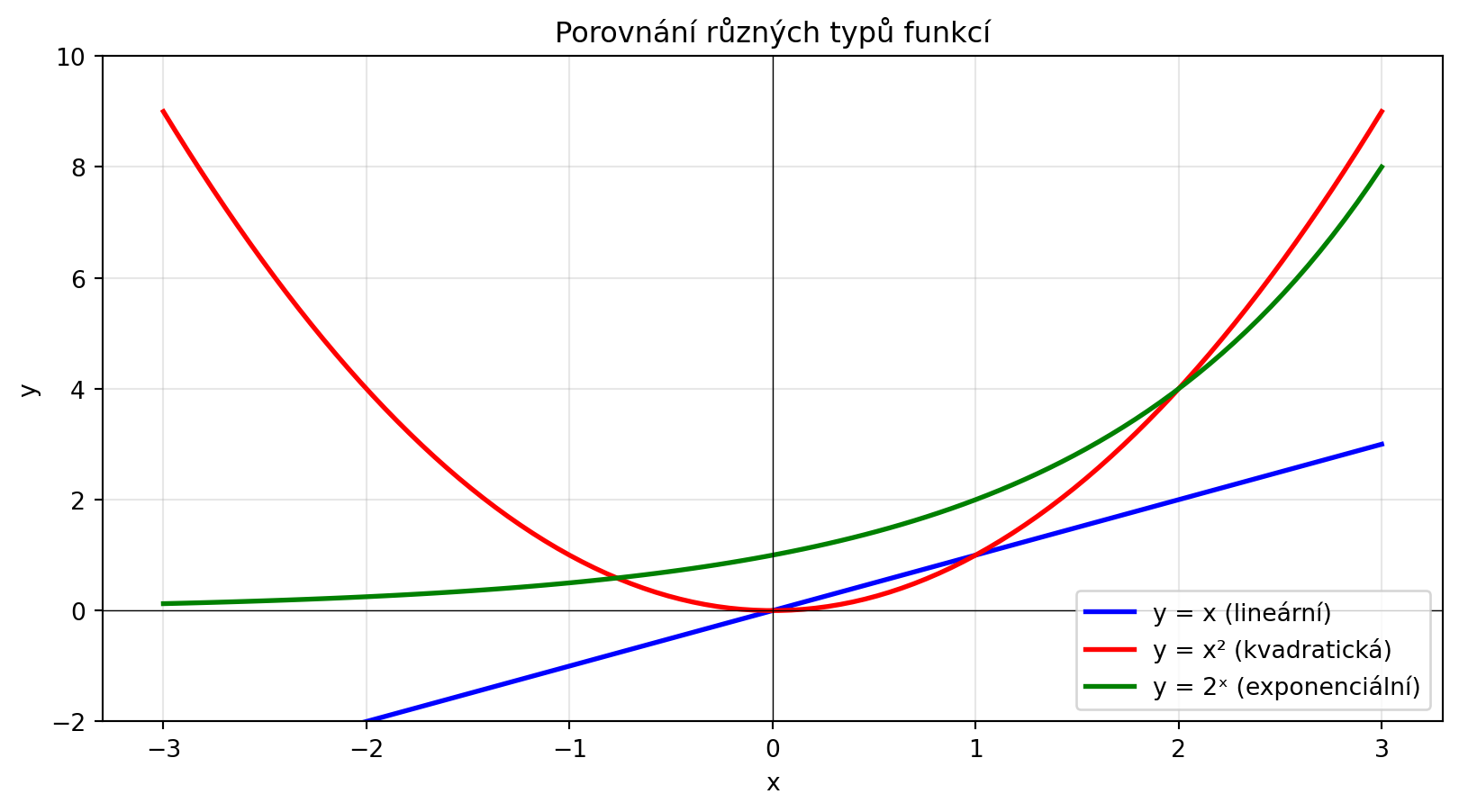
Svět kolem nás často není lineární. Populace roste exponenciálně, radioaktivní látky se rozpadají, a neuronové sítě používají nelineární aktivační funkce.
```{python}
#| fig-cap: "Lineární vs. nelineární funkce"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
plt.figure(figsize=(10, 5))
plt.plot(x, x, 'b-', linewidth=2, label='y = x (lineární)')
plt.plot(x, x**2, 'r-', linewidth=2, label='y = x² (kvadratická)')
plt.plot(x, 2**x, 'g-', linewidth=2, label='y = 2ˣ (exponenciální)')
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Porovnání různých typů funkcí')
plt.legend()
plt.ylim(-2, 10)
plt.show()
```
---
## Kvadratická funkce
**Kvadratická funkce** má tvar:
$$f(x) = ax^2 + bx + c$$
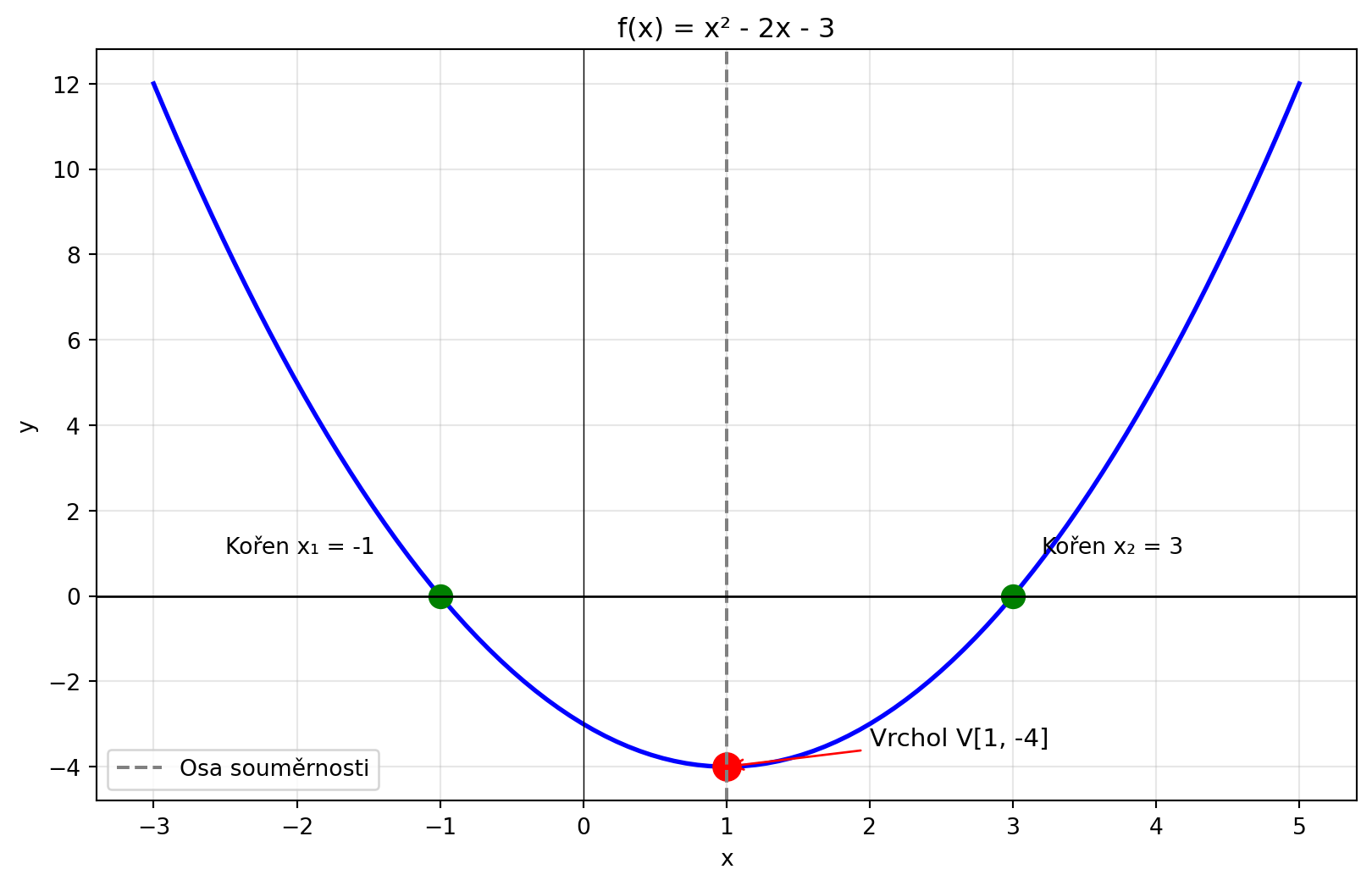
Její graf je **parabola**.
```{python}
#| fig-cap: "Parabola a její části"
#| code-fold: true
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 5, 100)
y = (x - 1)**2 - 4 # Ekvivalent x² - 2x - 3
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(x, y, 'b-', linewidth=2)
# Vrchol
ax.plot(1, -4, 'ro', markersize=12)
ax.annotate('Vrchol V[1, -4]', xy=(1, -4), xytext=(2, -3.5),
fontsize=11, arrowprops=dict(arrowstyle='->', color='red'))
# Osa souměrnosti
ax.axvline(x=1, color='gray', linestyle='--', label='Osa souměrnosti')
# Průsečíky s osou x (kořeny)
ax.plot([-1, 3], [0, 0], 'go', markersize=10)
ax.annotate('Kořen x₁ = -1', xy=(-1, 0), xytext=(-2.5, 1), fontsize=10)
ax.annotate('Kořen x₂ = 3', xy=(3, 0), xytext=(3.2, 1), fontsize=10)
ax.axhline(y=0, color='k', linewidth=1)
ax.axvline(x=0, color='k', linewidth=0.5)
ax.grid(True, alpha=0.3)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('f(x) = x² - 2x - 3')
ax.legend()
plt.show()
```
### Vrchol paraboly
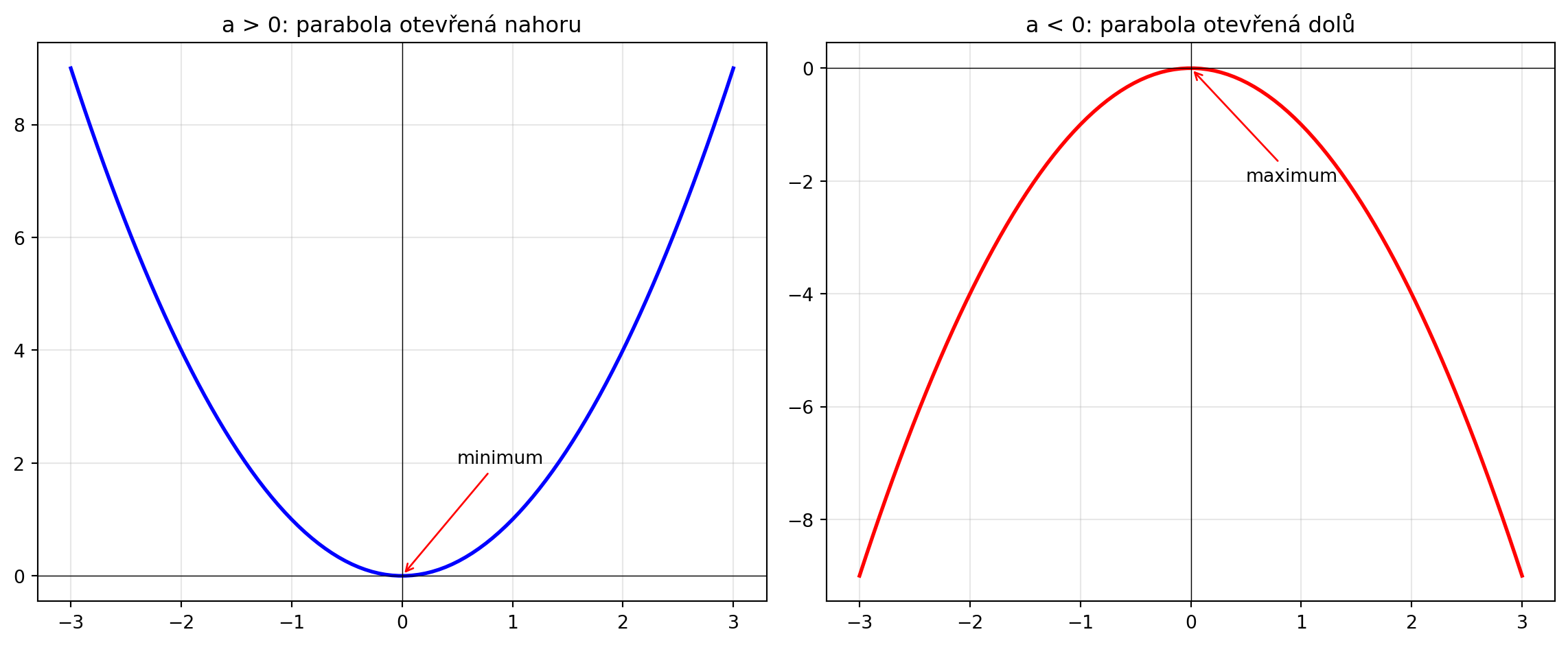
Vrchol je nejnižší (pro a > 0) nebo nejvyšší (pro a < 0) bod paraboly:
$$x_v = -\frac{b}{2a}, \quad y_v = f(x_v)$$
```{python}
def vrchol_paraboly(a, b, c):
"""Vypočítá souřadnice vrcholu paraboly."""
x_v = -b / (2 * a)
y_v = a * x_v**2 + b * x_v + c
return x_v, y_v
# Příklad: f(x) = 2x² - 8x + 5
a, b, c = 2, -8, 5
V = vrchol_paraboly(a, b, c)
print(f"Vrchol paraboly: V[{V[0]}, {V[1]}]")
```
### Kořeny kvadratické rovnice
Kořeny (průsečíky s osou x) najdeme pomocí **diskriminantu**:
$$D = b^2 - 4ac$$
$$x_{1,2} = \frac{-b \pm \sqrt{D}}{2a}$$
```{python}
import numpy as np
def koreny_kvadraticke_rovnice(a, b, c):
"""Najde kořeny kvadratické rovnice ax² + bx + c = 0."""
D = b**2 - 4*a*c
if D < 0:
return None, None, "Žádné reálné kořeny"
elif D == 0:
x = -b / (2*a)
return x, x, "Jeden dvojnásobný kořen"
else:
x1 = (-b + np.sqrt(D)) / (2*a)
x2 = (-b - np.sqrt(D)) / (2*a)
return x1, x2, "Dva různé kořeny"
# Příklady
print("x² - 5x + 6 = 0:")
x1, x2, typ = koreny_kvadraticke_rovnice(1, -5, 6)
print(f" {typ}: x₁ = {x1}, x₂ = {x2}")
print("\nx² + 4x + 4 = 0:")
x1, x2, typ = koreny_kvadraticke_rovnice(1, 4, 4)
print(f" {typ}: x = {x1}")
print("\nx² + x + 1 = 0:")
x1, x2, typ = koreny_kvadraticke_rovnice(1, 1, 1)
print(f" {typ}")
```
### Směr paraboly
```{python}
#| fig-cap: "Parabola otevřená nahoru vs. dolů"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
# a > 0
axes[0].plot(x, x**2, 'b-', linewidth=2)
axes[0].set_title('a > 0: parabola otevřená nahoru', fontsize=12)
axes[0].annotate('minimum', xy=(0, 0), xytext=(0.5, 2),
arrowprops=dict(arrowstyle='->', color='red'))
axes[0].grid(True, alpha=0.3)
axes[0].axhline(y=0, color='k', linewidth=0.5)
axes[0].axvline(x=0, color='k', linewidth=0.5)
# a < 0
axes[1].plot(x, -x**2, 'r-', linewidth=2)
axes[1].set_title('a < 0: parabola otevřená dolů', fontsize=12)
axes[1].annotate('maximum', xy=(0, 0), xytext=(0.5, -2),
arrowprops=dict(arrowstyle='->', color='red'))
axes[1].grid(True, alpha=0.3)
axes[1].axhline(y=0, color='k', linewidth=0.5)
axes[1].axvline(x=0, color='k', linewidth=0.5)
plt.tight_layout()
plt.show()
```
---
## Mocninné funkce
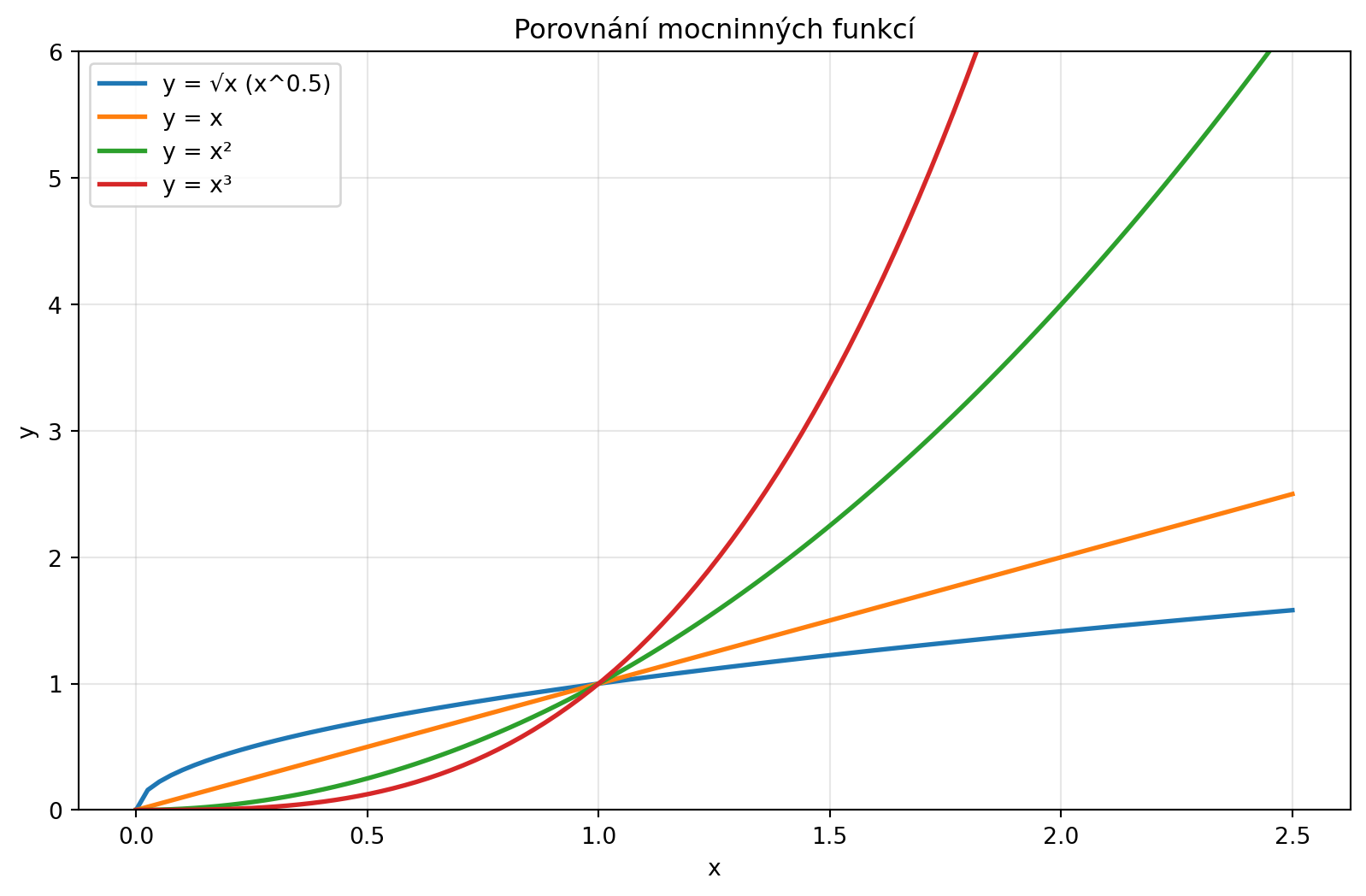
**Mocninná funkce** má tvar $f(x) = x^n$, kde n je exponent.
```{python}
#| fig-cap: "Mocninné funkce"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 2.5, 100)
plt.figure(figsize=(10, 6))
plt.plot(x, x**0.5, label='y = √x (x^0.5)', linewidth=2)
plt.plot(x, x, label='y = x', linewidth=2)
plt.plot(x, x**2, label='y = x²', linewidth=2)
plt.plot(x, x**3, label='y = x³', linewidth=2)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Porovnání mocninných funkcí')
plt.legend()
plt.ylim(0, 6)
plt.show()
```
::: {.callout-note title="Vlastnosti mocninných funkcí"}
| Exponent | Název | Vlastnosti |
|----------|-------|------------|
| n = 0.5 | Odmocnina | Roste pomalu, definována jen pro x ≥ 0 |
| n = 1 | Lineární | Přímka |
| n = 2 | Kvadratická | Parabola |
| n = 3 | Kubická | Inflexní bod v počátku |
| n = -1 | Hyperbola | 1/x, nedefinována v 0 |
:::
---
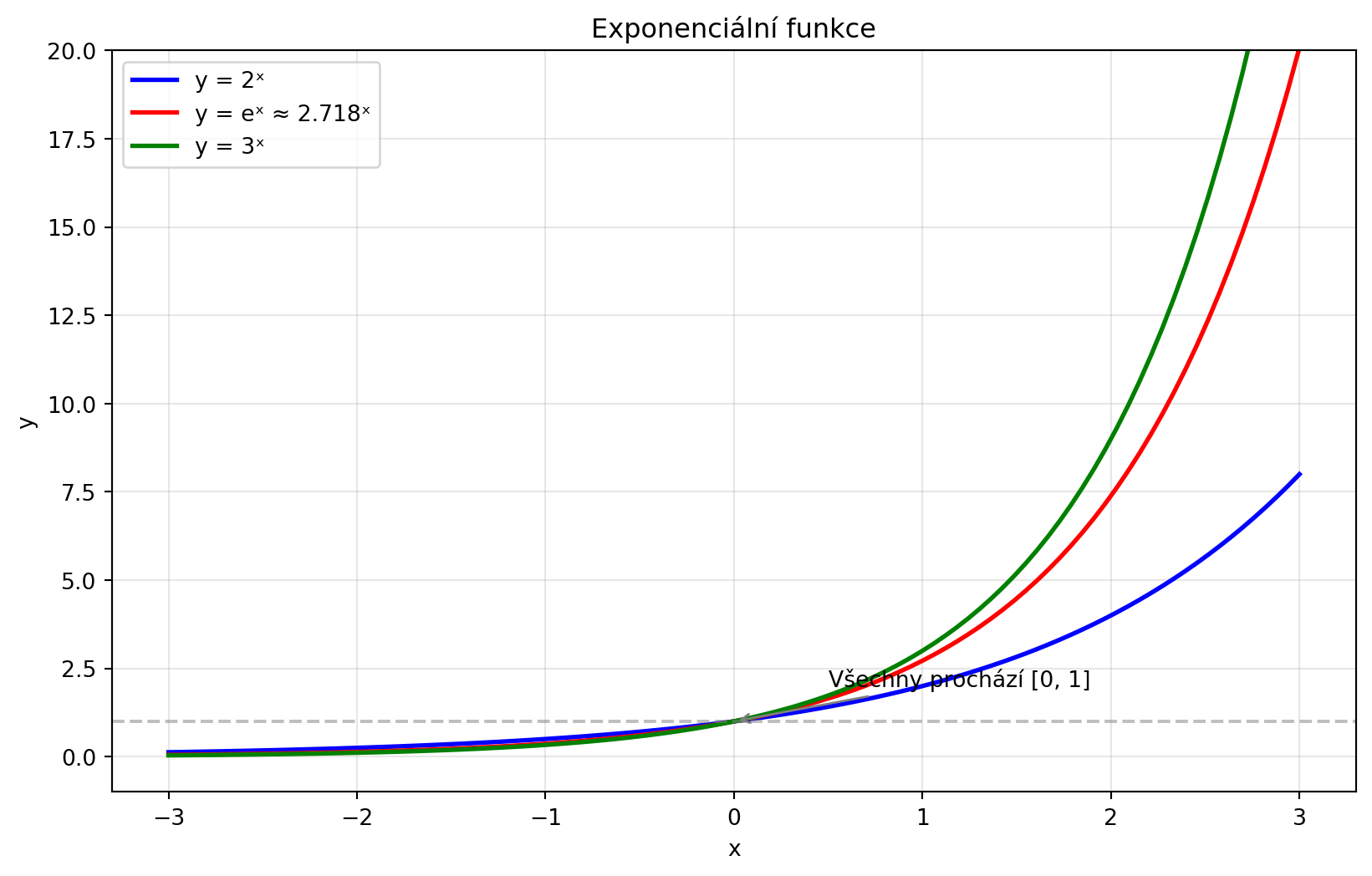
## Exponenciální funkce
**Exponenciální funkce** má tvar:
$$f(x) = a^x$$
kde $a > 0$ je základ a $x$ je exponent.
Nejdůležitější případ: $f(x) = e^x$, kde $e \approx 2.718$ (Eulerovo číslo).
```{python}
#| fig-cap: "Exponenciální funkce"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
plt.figure(figsize=(10, 6))
plt.plot(x, 2**x, 'b-', linewidth=2, label='y = 2ˣ')
plt.plot(x, np.exp(x), 'r-', linewidth=2, label='y = eˣ ≈ 2.718ˣ')
plt.plot(x, 3**x, 'g-', linewidth=2, label='y = 3ˣ')
plt.axhline(y=1, color='gray', linestyle='--', alpha=0.5)
plt.annotate('Všechny prochází [0, 1]', xy=(0, 1), xytext=(0.5, 2),
fontsize=10, arrowprops=dict(arrowstyle='->', color='gray'))
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Exponenciální funkce')
plt.legend()
plt.ylim(-1, 20)
plt.show()
```
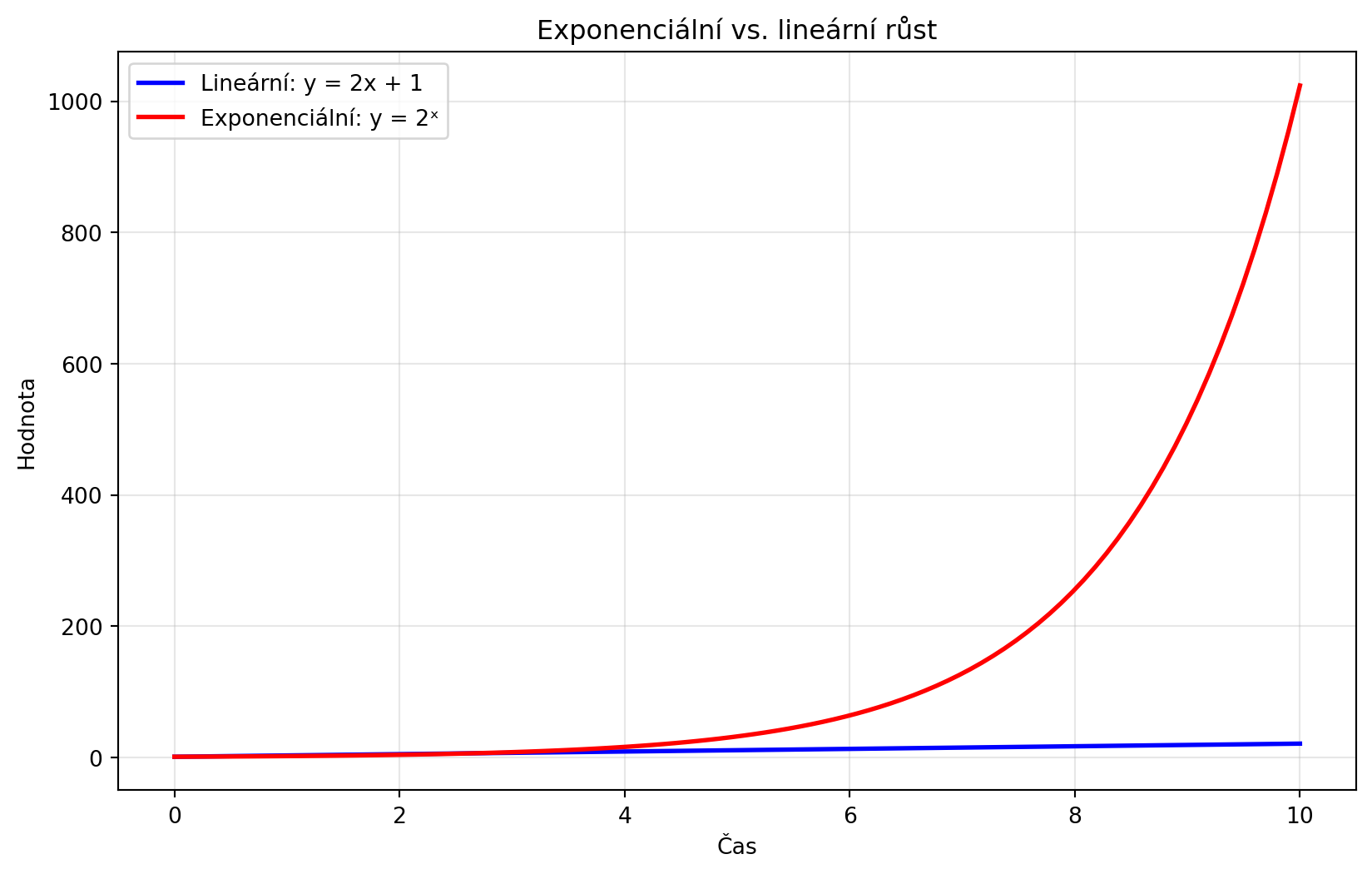
### Exponenciální růst
Exponenciální růst je velmi rychlý -- hodnota se za konstantní čas zdvojnásobí.
```{python}
#| fig-cap: "Exponenciální růst vs. lineární"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 10, 100)
plt.figure(figsize=(10, 6))
plt.plot(x, 2*x + 1, 'b-', linewidth=2, label='Lineární: y = 2x + 1')
plt.plot(x, 2**x, 'r-', linewidth=2, label='Exponenciální: y = 2ˣ')
plt.grid(True, alpha=0.3)
plt.xlabel('Čas')
plt.ylabel('Hodnota')
plt.title('Exponenciální vs. lineární růst')
plt.legend()
plt.show()
```
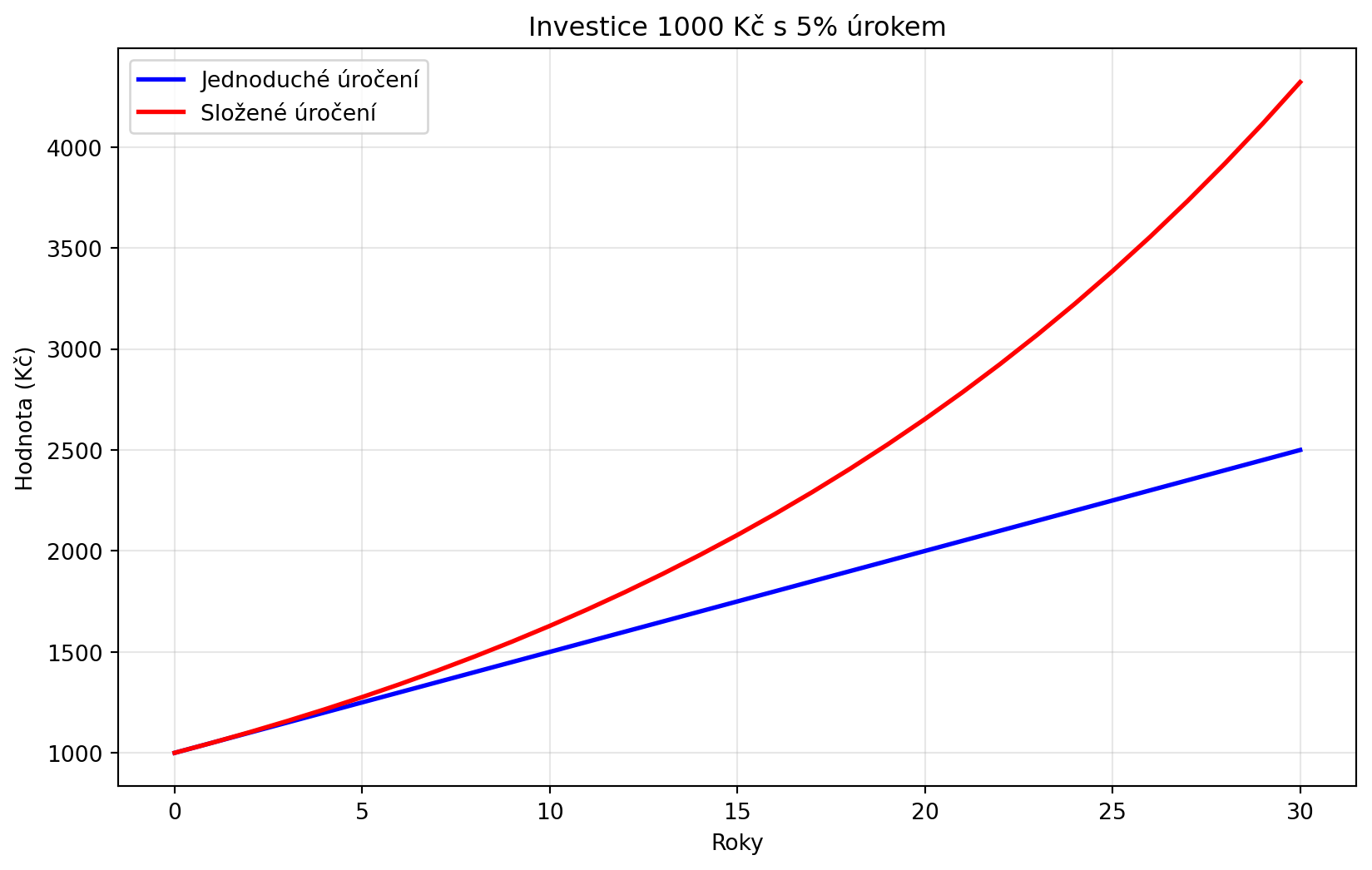
::: {.callout-tip title="Příklad: Složené úročení"}
Pokud investujete 1000 Kč s 5% ročním úrokem:
- **Jednoduché úročení** (lineární): $1000 + 1000 \times 0.05 \times t$
- **Složené úročení** (exponenciální): $1000 \times 1.05^t$
:::
```{python}
#| fig-cap: "Jednoduché vs. složené úročení"
import numpy as np
import matplotlib.pyplot as plt
roky = np.arange(0, 31)
pocatek = 1000
urok = 0.05
jednoduche = pocatek + pocatek * urok * roky
slozene = pocatek * (1 + urok) ** roky
plt.figure(figsize=(10, 6))
plt.plot(roky, jednoduche, 'b-', linewidth=2, label='Jednoduché úročení')
plt.plot(roky, slozene, 'r-', linewidth=2, label='Složené úročení')
plt.xlabel('Roky')
plt.ylabel('Hodnota (Kč)')
plt.title('Investice 1000 Kč s 5% úrokem')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
print(f"Po 30 letech - jednoduché: {jednoduche[-1]:.0f} Kč")
print(f"Po 30 letech - složené: {slozene[-1]:.0f} Kč")
```
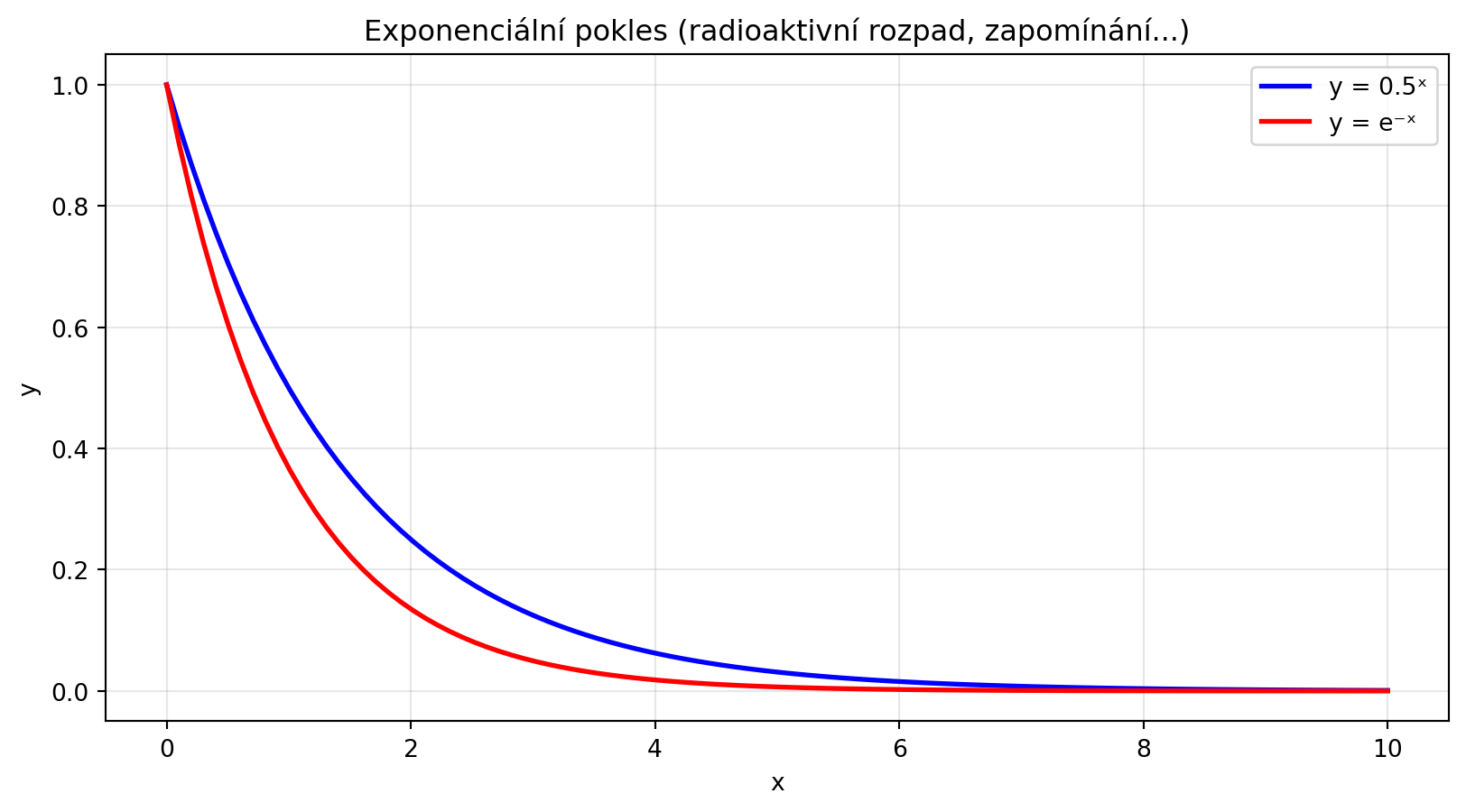
### Exponenciální pokles
Pro základ 0 < a < 1 funkce klesá:
```{python}
#| fig-cap: "Exponenciální pokles"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 10, 100)
plt.figure(figsize=(10, 5))
plt.plot(x, 0.5**x, 'b-', linewidth=2, label='y = 0.5ˣ')
plt.plot(x, np.exp(-x), 'r-', linewidth=2, label='y = e⁻ˣ')
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Exponenciální pokles (radioaktivní rozpad, zapomínání...)')
plt.legend()
plt.show()
```
---
## Logaritmus
**Logaritmus** je opačná operace k exponenciále:
$$\text{Pokud } a^y = x, \text{ pak } \log_a(x) = y$$
```{python}
# Příklad: 2³ = 8, tedy log₂(8) = 3
import numpy as np
print(f"2³ = {2**3}")
print(f"log₂(8) = {np.log2(8)}")
# e^2 ≈ 7.389, tedy ln(7.389) ≈ 2
print(f"\ne² = {np.exp(2):.3f}")
print(f"ln({np.exp(2):.3f}) = {np.log(np.exp(2)):.1f}")
```
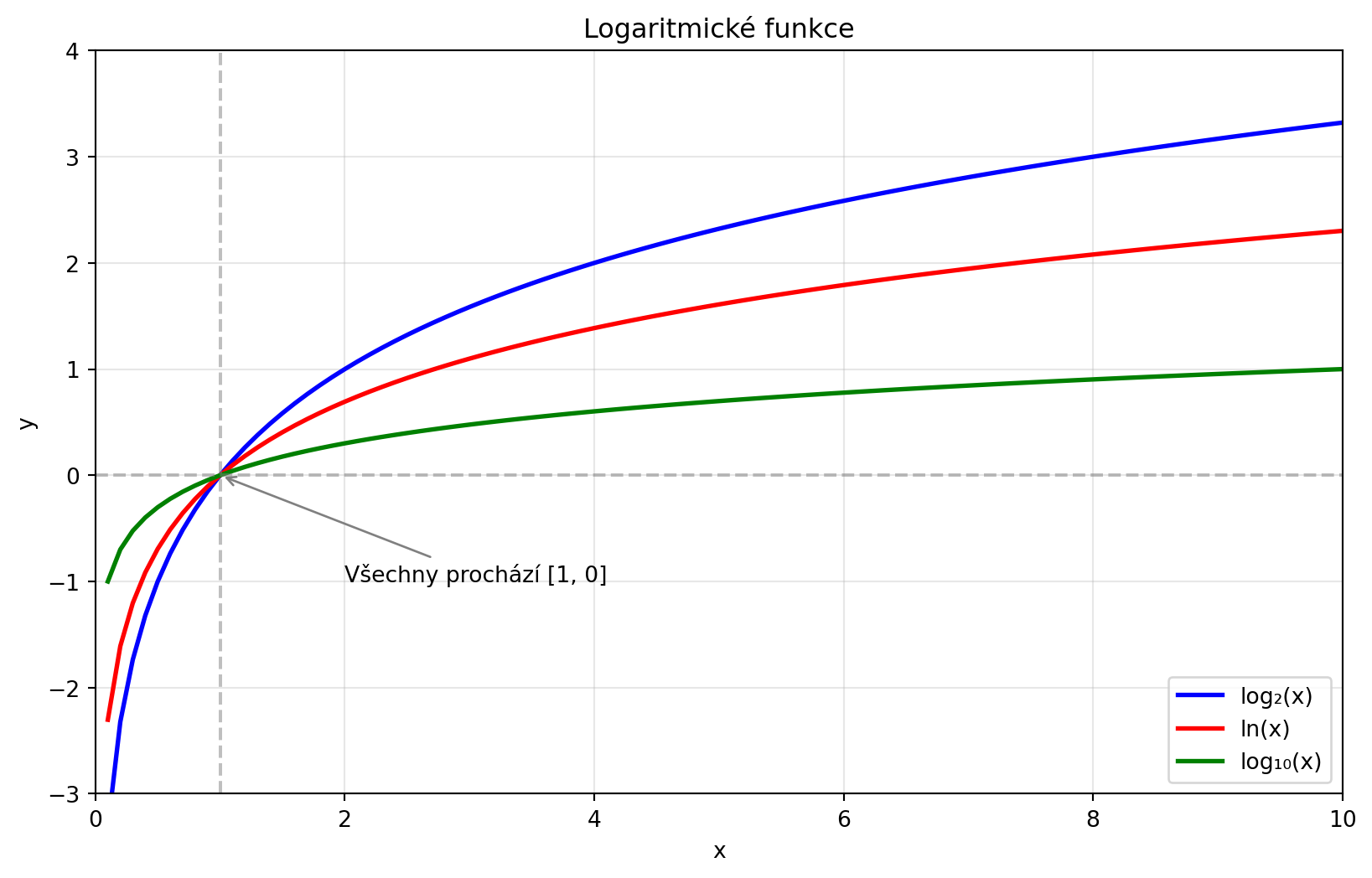
### Typy logaritmů
| Zápis | Základ | Název | V Pythonu |
|-------|--------|-------|-----------|
| log₂(x) | 2 | Dvojkový logaritmus | `np.log2(x)` |
| ln(x) | e | Přirozený logaritmus | `np.log(x)` |
| log₁₀(x) | 10 | Dekadický logaritmus | `np.log10(x)` |
```{python}
#| fig-cap: "Logaritmické funkce"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0.1, 10, 100)
plt.figure(figsize=(10, 6))
plt.plot(x, np.log2(x), 'b-', linewidth=2, label='log₂(x)')
plt.plot(x, np.log(x), 'r-', linewidth=2, label='ln(x)')
plt.plot(x, np.log10(x), 'g-', linewidth=2, label='log₁₀(x)')
plt.axhline(y=0, color='gray', linestyle='--', alpha=0.5)
plt.axvline(x=1, color='gray', linestyle='--', alpha=0.5)
plt.annotate('Všechny prochází [1, 0]', xy=(1, 0), xytext=(2, -1),
fontsize=10, arrowprops=dict(arrowstyle='->', color='gray'))
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Logaritmické funkce')
plt.legend()
plt.xlim(0, 10)
plt.ylim(-3, 4)
plt.show()
```
### Vlastnosti logaritmu
::: {.callout-note title="Základní vlastnosti"}
1. $\log(a \cdot b) = \log(a) + \log(b)$
2. $\log(a / b) = \log(a) - \log(b)$
3. $\log(a^n) = n \cdot \log(a)$
4. $\log_a(1) = 0$
5. $\log_a(a) = 1$
:::
```{python}
# Ověření vlastností
import numpy as np
print("Vlastnost 1: log(ab) = log(a) + log(b)")
print(f" log(6) = {np.log(6):.4f}")
print(f" log(2) + log(3) = {np.log(2) + np.log(3):.4f}")
print("\nVlastnost 3: log(a^n) = n·log(a)")
print(f" log(8) = log(2³) = {np.log(8):.4f}")
print(f" 3·log(2) = {3 * np.log(2):.4f}")
```
---
## Aplikace v praxi
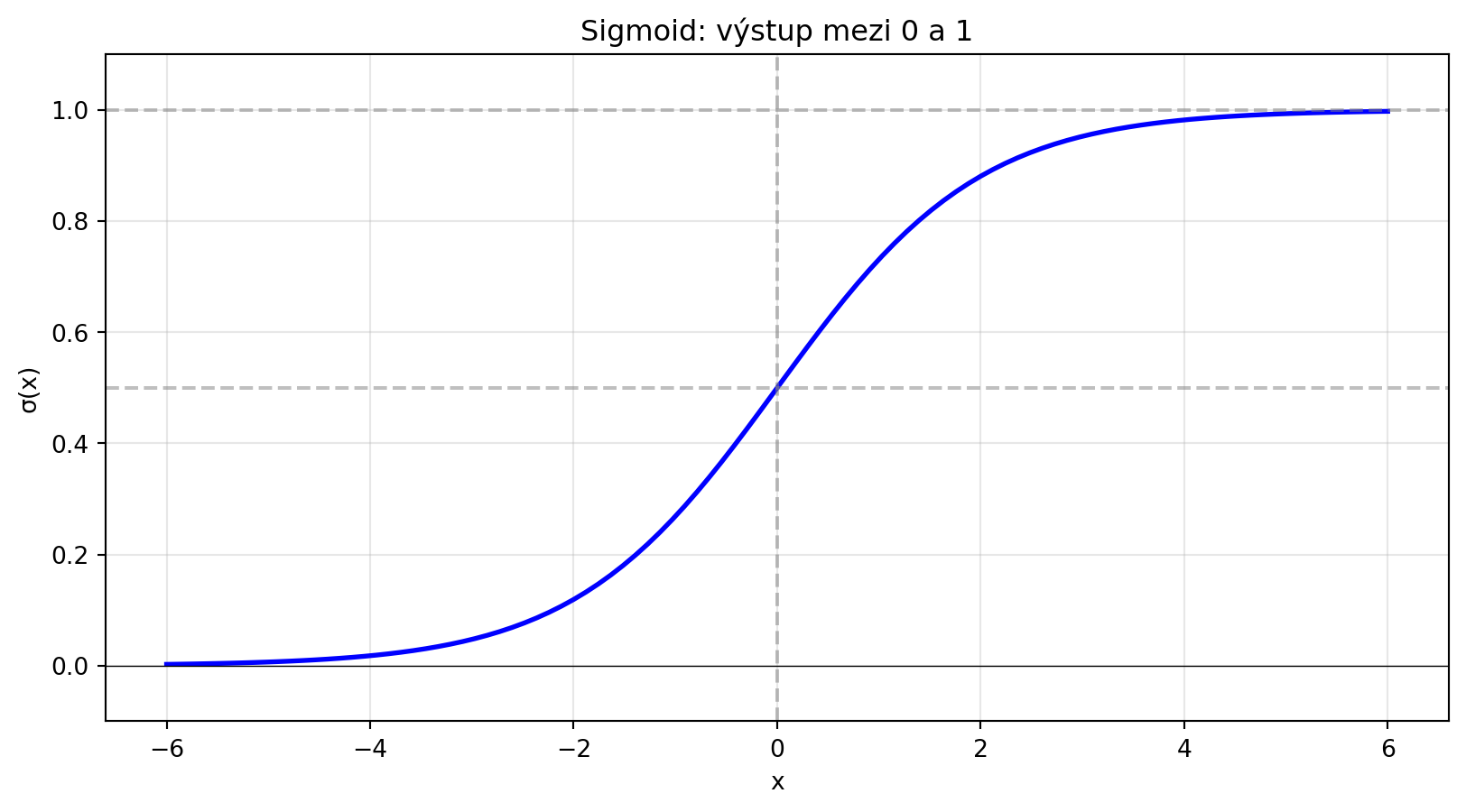
### Sigmoid -- aktivační funkce
**Sigmoid** (logistická funkce) je klíčová v neuronových sítích:
$$\sigma(x) = \frac{1}{1 + e^{-x}}$$
```{python}
#| fig-cap: "Sigmoid funkce"
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.linspace(-6, 6, 100)
plt.figure(figsize=(10, 5))
plt.plot(x, sigmoid(x), 'b-', linewidth=2)
plt.axhline(y=0.5, color='gray', linestyle='--', alpha=0.5)
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axhline(y=1, color='gray', linestyle='--', alpha=0.5)
plt.axvline(x=0, color='gray', linestyle='--', alpha=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('σ(x)')
plt.title('Sigmoid: výstup mezi 0 a 1')
plt.ylim(-0.1, 1.1)
plt.show()
```
::: {.callout-tip title="Proč sigmoid?"}
Sigmoid převádí libovolné reálné číslo na hodnotu mezi 0 a 1. Používá se pro:
- **Binární klasifikaci** -- pravděpodobnost, že výstup je 1
- **Logistická regrese** -- základní model klasifikace
- **Gating mechanismy** v sítích LSTM
:::
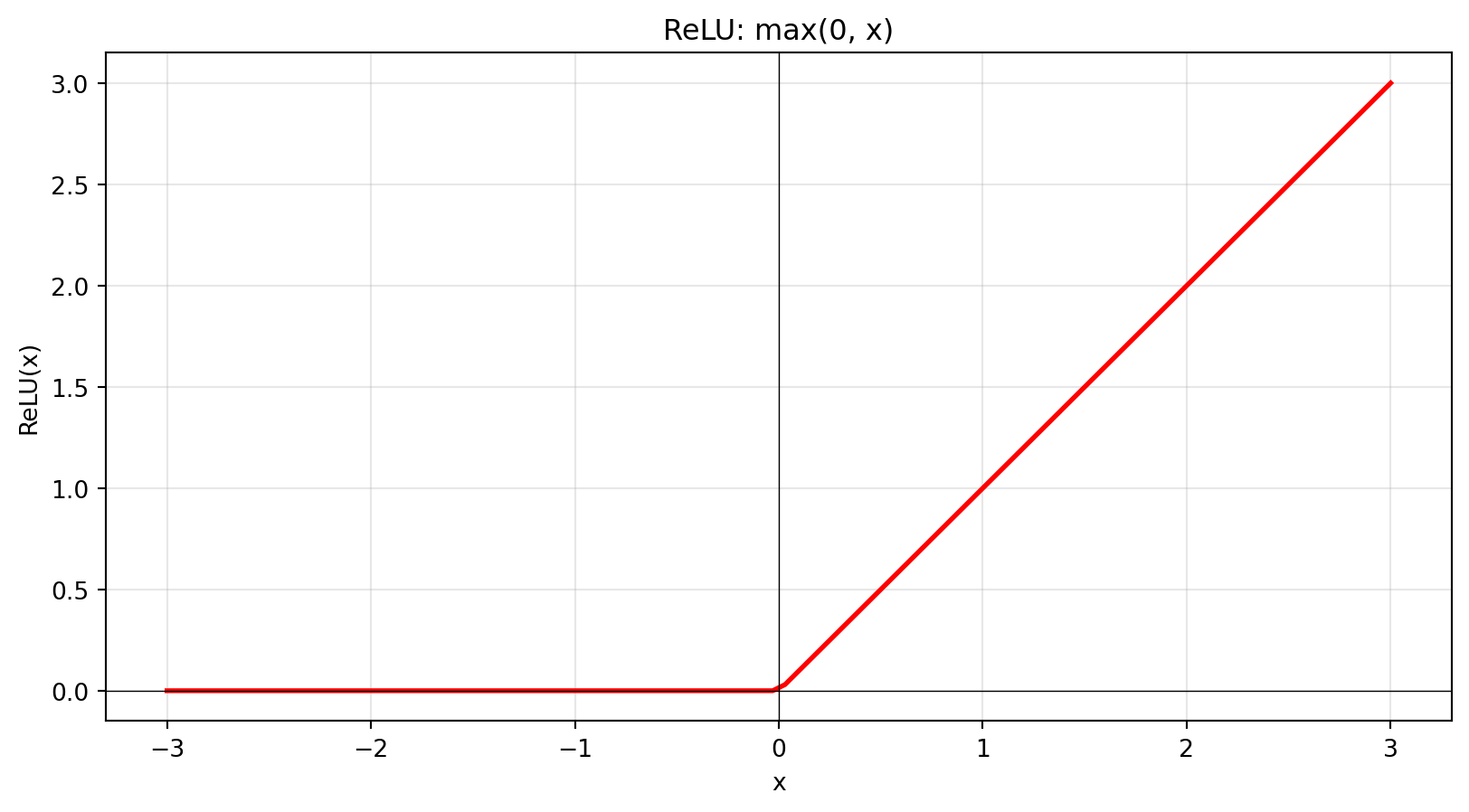
### ReLU -- nejpopulárnější aktivační funkce
**ReLU** (Rectified Linear Unit) je ještě jednodušší:
$$\text{ReLU}(x) = \max(0, x)$$
```{python}
#| fig-cap: "ReLU funkce"
import numpy as np
import matplotlib.pyplot as plt
def relu(x):
return np.maximum(0, x)
x = np.linspace(-3, 3, 100)
plt.figure(figsize=(10, 5))
plt.plot(x, relu(x), 'r-', linewidth=2)
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('ReLU(x)')
plt.title('ReLU: max(0, x)')
plt.show()
```
### Softmax -- pravděpodobnosti
**Softmax** převádí vektor čísel na pravděpodobnosti:
$$\text{softmax}(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}}$$
```{python}
import numpy as np
def softmax(x):
"""Převede vektor na pravděpodobnosti."""
exp_x = np.exp(x)
return exp_x / np.sum(exp_x)
# Příklad: skóre pro 3 třídy
skore = np.array([2.0, 1.0, 0.1])
pravdepodobnosti = softmax(skore)
print("Skóre: ", skore)
print("Pravděpodobnosti:", np.round(pravdepodobnosti, 3))
print("Součet: ", np.sum(pravdepodobnosti))
```
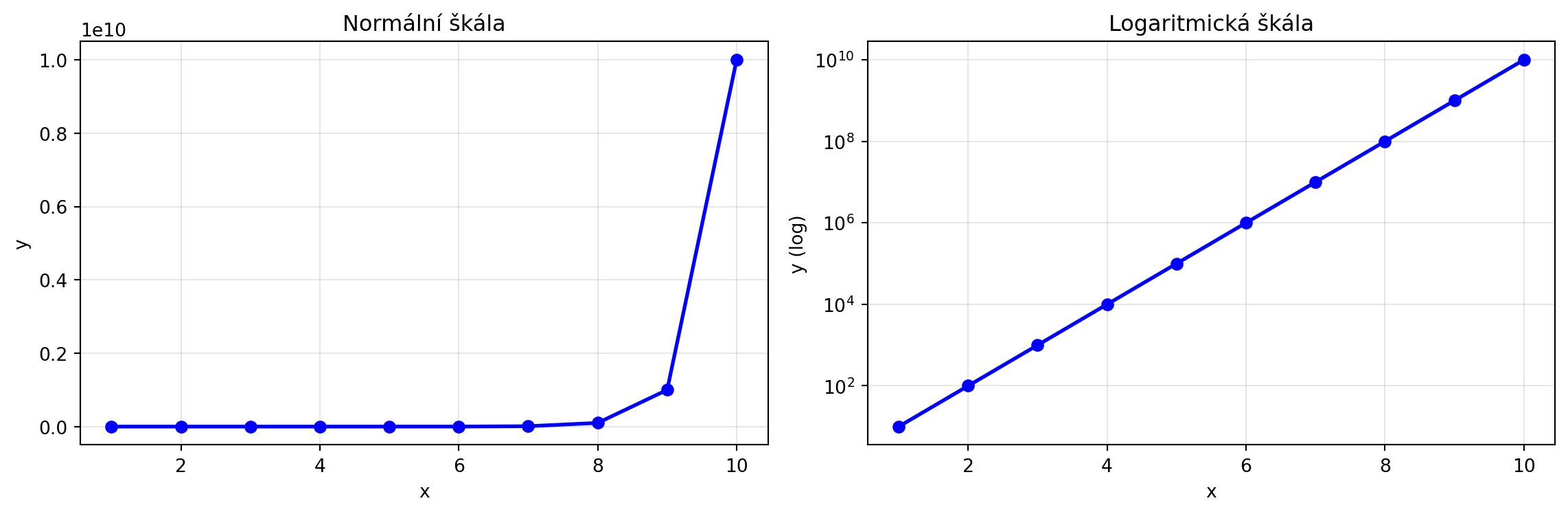
### Logaritmická škála
Pro zobrazení dat s velkým rozsahem používáme logaritmickou škálu:
```{python}
#| fig-cap: "Normální vs. logaritmická škála"
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(1, 11)
y = 10**x # Exponenciální data
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].plot(x, y, 'bo-', linewidth=2)
axes[0].set_title('Normální škála')
axes[0].set_xlabel('x')
axes[0].set_ylabel('y')
axes[0].grid(True, alpha=0.3)
axes[1].plot(x, y, 'bo-', linewidth=2)
axes[1].set_yscale('log')
axes[1].set_title('Logaritmická škála')
axes[1].set_xlabel('x')
axes[1].set_ylabel('y (log)')
axes[1].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
---
## Řešené příklady
### Příklad 1: Kořeny kvadratické rovnice
Řešte rovnici $x^2 - 4x - 5 = 0$.
```{python}
import numpy as np
a, b, c = 1, -4, -5
D = b**2 - 4*a*c
print(f"Diskriminant D = {b}² - 4·{a}·{c} = {D}")
x1 = (-b + np.sqrt(D)) / (2*a)
x2 = (-b - np.sqrt(D)) / (2*a)
print(f"x₁ = (-({b}) + √{D}) / (2·{a}) = {x1}")
print(f"x₂ = (-({b}) - √{D}) / (2·{a}) = {x2}")
```
### Příklad 2: Vrchol paraboly
Najděte vrchol paraboly $f(x) = -2x^2 + 8x - 3$.
```{python}
a, b, c = -2, 8, -3
x_v = -b / (2*a)
y_v = a*x_v**2 + b*x_v + c
print(f"x_v = -{b} / (2·{a}) = {x_v}")
print(f"y_v = f({x_v}) = {a}·{x_v}² + {b}·{x_v} + {c} = {y_v}")
print(f"\nVrchol: V[{x_v}, {y_v}]")
print(f"Parabola má maximum (a < 0)")
```
### Příklad 3: Exponenciální růst
Populace bakterií se zdvojnásobí každé 2 hodiny. Začínáme s 1000 bakteriemi. Kolik jich bude za 10 hodin?
```{python}
pocatek = 1000
zdvojeni = 2 # hodiny
cas = 10 # hodiny
# Za čas t se populace zdvojnásobí t/zdvojeni krát
pocet_zdvojeni = cas / zdvojeni
konec = pocatek * 2**pocet_zdvojeni
print(f"Počet zdvojení: {pocet_zdvojeni}")
print(f"Počet bakterií po {cas} hodinách: {konec:.0f}")
```
### Příklad 4: Logaritmická rovnice
Řešte rovnici $\log_2(x) = 5$.
```{python}
# log₂(x) = 5 znamená 2⁵ = x
import numpy as np
x = 2**5
print(f"log₂(x) = 5")
print(f"x = 2⁵ = {x}")
# Ověření
print(f"Ověření: log₂({x}) = {np.log2(x)}")
```
### Příklad 5: Sigmoid a pravděpodobnost
Neuron produkuje hodnotu z = 2.5. Jaká je pravděpodobnost po aplikaci sigmoidu?
```{python}
z = 2.5
p = sigmoid(z)
print(f"sigmoid({z}) = 1 / (1 + e^(-{z})) = {p:.4f}")
print(f"Pravděpodobnost: {p*100:.1f}%")
```
---
## Cvičení
::: {.callout-warning title="Cvičení 1: Vrchol paraboly"}
Najděte vrchol paraboly $f(x) = x^2 - 6x + 5$ a určete, zda jde o minimum nebo maximum.
**Výsledek:** V[3, -4], minimum
<details>
<summary>Řešení</summary>
$x_v = \frac{6}{2 \cdot 1} = 3$
$y_v = 9 - 18 + 5 = -4$
Minimum (a = 1 > 0)
</details>
:::
::: {.callout-warning title="Cvičení 2: Kořeny"}
Řešte rovnici $2x^2 - 7x + 3 = 0$.
**Výsledek:** x₁ = 3, x₂ = 0.5
:::
::: {.callout-warning title="Cvičení 3: Exponenciální růst"}
Investice 10 000 Kč roste o 8% ročně. Jaká bude hodnota za 5 let?
**Výsledek:** přibližně 14 693 Kč
<details>
<summary>Řešení</summary>
$10000 \times 1.08^5 = 14693.28$ Kč
</details>
:::
::: {.callout-warning title="Cvičení 4: Logaritmus"}
Vypočítejte bez kalkulačky:
a) $\log_2(32)$
b) $\log_{10}(1000)$
c) $\ln(e^5)$
**Výsledky:** 5, 3, 5
:::
::: {.callout-warning title="Cvičení 5: Sigmoid"}
Pro jakou hodnotu x platí $\sigma(x) = 0.5$?
**Výsledek:** x = 0
<details>
<summary>Řešení</summary>
$\sigma(x) = 0.5$ když $e^{-x} = 1$, což platí pro $x = 0$.
</details>
:::
::: {.callout-warning title="Cvičení 6: Graf funkce"}
Nakreslete graf funkce $f(x) = e^{-x^2}$ (Gaussova křivka) pro x od -3 do 3.
<details>
<summary>Řešení</summary>
```python
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
y = np.exp(-x**2)
plt.plot(x, y)
plt.title('Gaussova křivka')
plt.grid(True)
plt.show()
```
</details>
:::
---
## Shrnutí
::: {.callout-note title="Co si zapamatovat"}
- **Kvadratická funkce**: $f(x) = ax^2 + bx + c$, graf je parabola
- **Vrchol paraboly**: $x_v = -\frac{b}{2a}$
- **Diskriminant**: $D = b^2 - 4ac$ určuje počet kořenů
- **Exponenciální funkce**: $f(x) = a^x$, rychlý růst/pokles
- **Logaritmus** je opak exponenciely: $\log_a(a^x) = x$
- **Sigmoid**: $\sigma(x) = \frac{1}{1+e^{-x}}$, výstup mezi 0 a 1
- **ReLU**: $\max(0, x)$, nejpopulárnější aktivační funkce
- **Softmax** převádí čísla na pravděpodobnosti
:::
V další části se ponoříme do světa **vektorů a matic** -- matematického jazyka, kterým "mluví" neuronové sítě.