# Pokročilé optimalizátory {#sec-pokrocile-optimalizatory}
## Motivace: Proč nestačí vanilla SGD?
Základní gradient descent má několik problémů:
1. **Oscilace** v úzkých údolích
2. **Pomalá konvergence** na plochých oblastech
3. **Stejný learning rate** pro všechny parametry
4. **Citlivost** na volbu learning rate
Pokročilé optimalizátory tyto problémy řeší pomocí různých technik. V této kapitole se podíváme na nejdůležitější z nich.
```{python}
import numpy as np
import matplotlib.pyplot as plt
# Demonstrace problému SGD
def ill_conditioned(x, y):
return x**2 + 20*y**2
def grad_ill(pos):
return np.array([2*pos[0], 40*pos[1]])
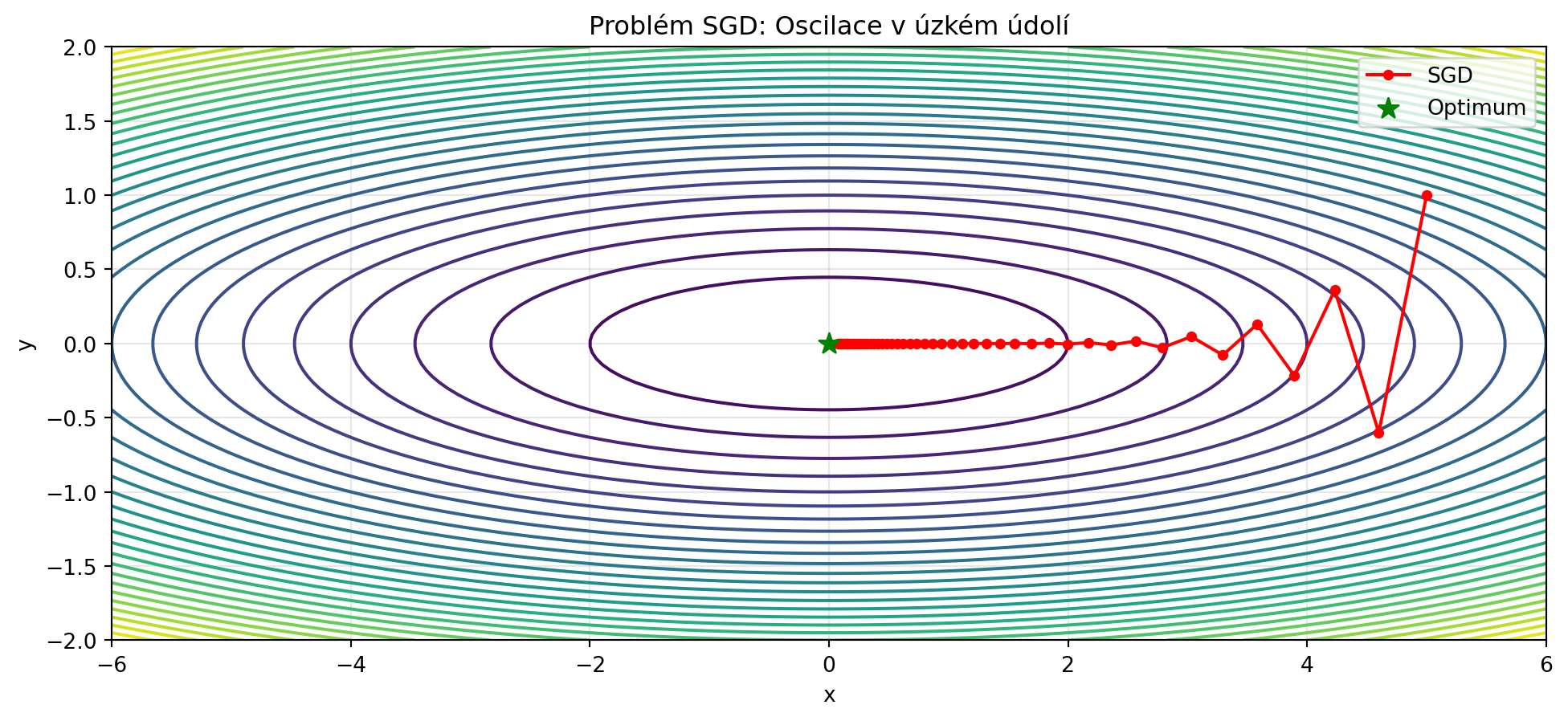
# SGD osciluje
pos = np.array([5.0, 1.0])
lr = 0.04
path_sgd = [pos.copy()]
for _ in range(50):
grad = grad_ill(pos)
pos = pos - lr * grad
path_sgd.append(pos.copy())
path_sgd = np.array(path_sgd)
# Vizualizace
x = np.linspace(-6, 6, 100)
y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x, y)
Z = ill_conditioned(X, Y)
plt.figure(figsize=(12, 5))
plt.contour(X, Y, Z, levels=30, cmap='viridis')
plt.plot(path_sgd[:, 0], path_sgd[:, 1], 'ro-', markersize=4, label='SGD')
plt.scatter([0], [0], color='green', s=100, marker='*', zorder=5, label='Optimum')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Problém SGD: Oscilace v úzkém údolí')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
print("SGD osciluje kolmo na směr k minimu!")
print("Potřebujeme chytřejší přístup...")
```
## Momentum
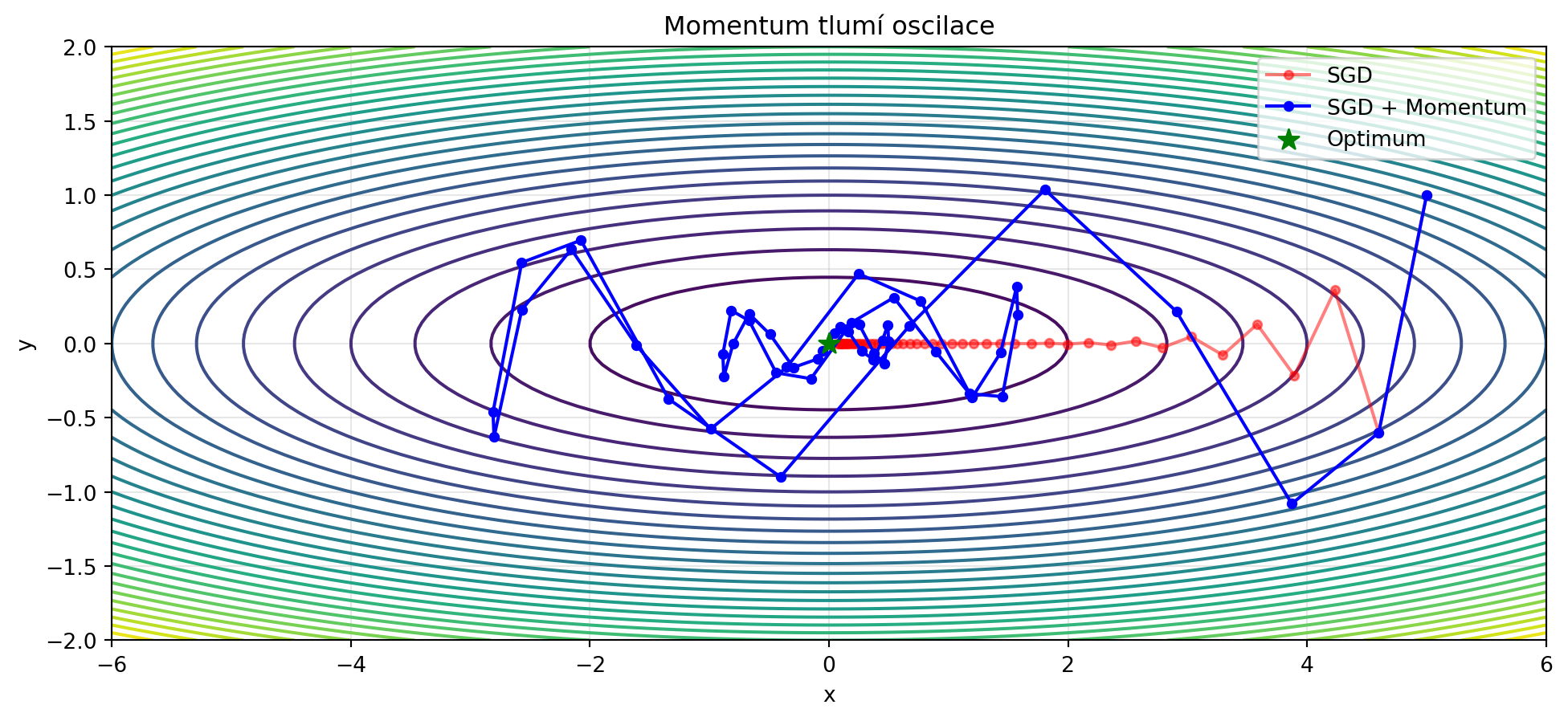
**Momentum** přidává "setrvačnost" - pamatuje si předchozí směr a pokračuje v něm:
::: {.callout-note}
## Algoritmus: SGD s Momentum
$$\mathbf{v}_{t+1} = \beta \mathbf{v}_t + \nabla f(\mathbf{w}_t)$$
$$\mathbf{w}_{t+1} = \mathbf{w}_t - \eta \mathbf{v}_{t+1}$$
kde $\beta \in [0, 1)$ je koeficient momentum (typicky 0.9).
:::
Momentum má dva efekty:
1. **Akcelerace** ve směru konzistentního gradientu
2. **Tlumení oscilací** v kolmém směru
```{python}
import numpy as np
import matplotlib.pyplot as plt
def sgd_momentum(grad_f, w0, lr=0.04, beta=0.9, n_iter=50):
"""SGD s momentum."""
w = np.array(w0, dtype=float)
v = np.zeros_like(w)
history = [w.copy()]
for _ in range(n_iter):
grad = grad_f(w)
v = beta * v + grad
w = w - lr * v
history.append(w.copy())
return np.array(history)
# Porovnání SGD a Momentum
path_momentum = sgd_momentum(grad_ill, [5.0, 1.0], lr=0.04, beta=0.9)
plt.figure(figsize=(12, 5))
plt.contour(X, Y, Z, levels=30, cmap='viridis')
plt.plot(path_sgd[:, 0], path_sgd[:, 1], 'ro-', markersize=4, alpha=0.5, label='SGD')
plt.plot(path_momentum[:, 0], path_momentum[:, 1], 'bo-', markersize=4, label='SGD + Momentum')
plt.scatter([0], [0], color='green', s=100, marker='*', zorder=5, label='Optimum')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Momentum tlumí oscilace')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
### Intuice: Míček valící se z kopce
```{python}
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 2, figsize=(14, 5))
# SGD - žádná paměť
ax1 = axes[0]
ax1.text(0.5, 0.8, 'SGD', transform=ax1.transAxes, fontsize=20, fontweight='bold', ha='center')
ax1.text(0.5, 0.5, 'Každý krok závisí\npouze na aktuálním gradientu\n\n"Jako robot bez paměti"',
transform=ax1.transAxes, fontsize=12, ha='center', va='center')
ax1.axis('off')
# Momentum - paměť
ax2 = axes[1]
ax2.text(0.5, 0.8, 'Momentum', transform=ax2.transAxes, fontsize=20, fontweight='bold', ha='center')
ax2.text(0.5, 0.5, 'Pamatuje si předchozí směr\na pokračuje v něm\n\n"Jako míček valící se z kopce"',
transform=ax2.transAxes, fontsize=12, ha='center', va='center')
ax2.axis('off')
plt.tight_layout()
plt.show()
```
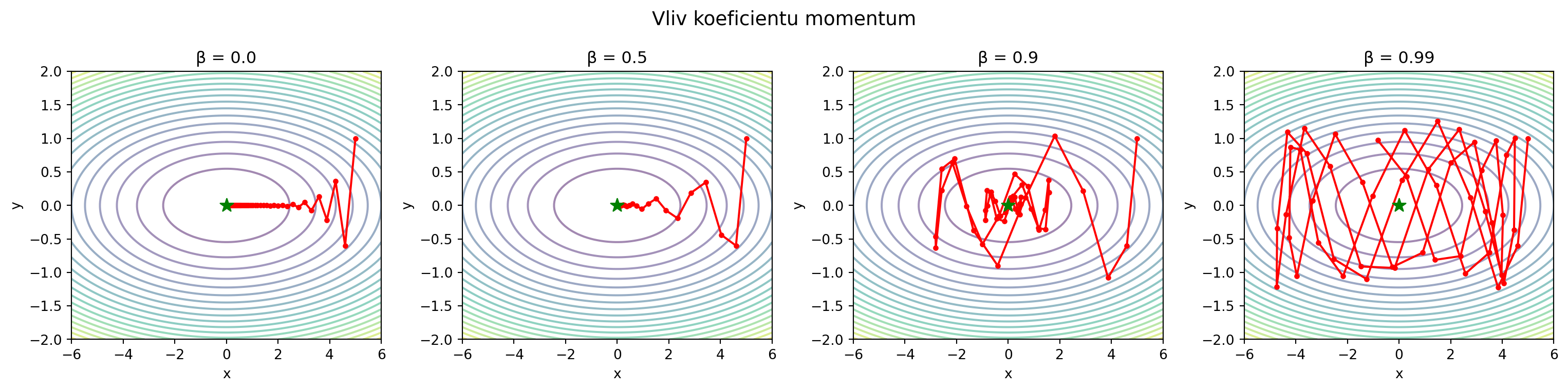
### Vliv parametru β
```{python}
import matplotlib.pyplot as plt
betas = [0.0, 0.5, 0.9, 0.99]
paths = {}
for beta in betas:
paths[beta] = sgd_momentum(grad_ill, [5.0, 1.0], lr=0.04, beta=beta, n_iter=50)
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
for ax, beta in zip(axes, betas):
ax.contour(X, Y, Z, levels=20, cmap='viridis', alpha=0.5)
ax.plot(paths[beta][:, 0], paths[beta][:, 1], 'ro-', markersize=3)
ax.scatter([0], [0], color='green', s=100, marker='*', zorder=5)
ax.set_title(f'β = {beta}')
ax.set_xlim(-6, 6)
ax.set_ylim(-2, 2)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.suptitle('Vliv koeficientu momentum', fontsize=14)
plt.tight_layout()
plt.show()
```
## Nesterov Accelerated Gradient (NAG)
Vylepšení momentum - nejprve se "podíváme dopředu", pak spočítáme gradient:
::: {.callout-note}
## Algoritmus: Nesterov Momentum
$$\mathbf{v}_{t+1} = \beta \mathbf{v}_t + \nabla f(\mathbf{w}_t - \eta \beta \mathbf{v}_t)$$
$$\mathbf{w}_{t+1} = \mathbf{w}_t - \eta \mathbf{v}_{t+1}$$
Rozdíl: Gradient počítáme v "budoucí" pozici.
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
def nesterov(grad_f, w0, lr=0.04, beta=0.9, n_iter=50):
"""Nesterov Accelerated Gradient."""
w = np.array(w0, dtype=float)
v = np.zeros_like(w)
history = [w.copy()]
for _ in range(n_iter):
# Pohled dopředu
w_lookahead = w - lr * beta * v
grad = grad_f(w_lookahead)
v = beta * v + grad
w = w - lr * v
history.append(w.copy())
return np.array(history)
path_nesterov = nesterov(grad_ill, [5.0, 1.0], lr=0.04, beta=0.9)
plt.figure(figsize=(12, 5))
plt.contour(X, Y, Z, levels=30, cmap='viridis')
plt.plot(path_sgd[:, 0], path_sgd[:, 1], 'ro-', markersize=3, alpha=0.3, label='SGD')
plt.plot(path_momentum[:, 0], path_momentum[:, 1], 'bo-', markersize=3, alpha=0.5, label='Momentum')
plt.plot(path_nesterov[:, 0], path_nesterov[:, 1], 'go-', markersize=4, label='Nesterov')
plt.scatter([0], [0], color='red', s=100, marker='*', zorder=5, label='Optimum')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Porovnání: SGD vs Momentum vs Nesterov')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
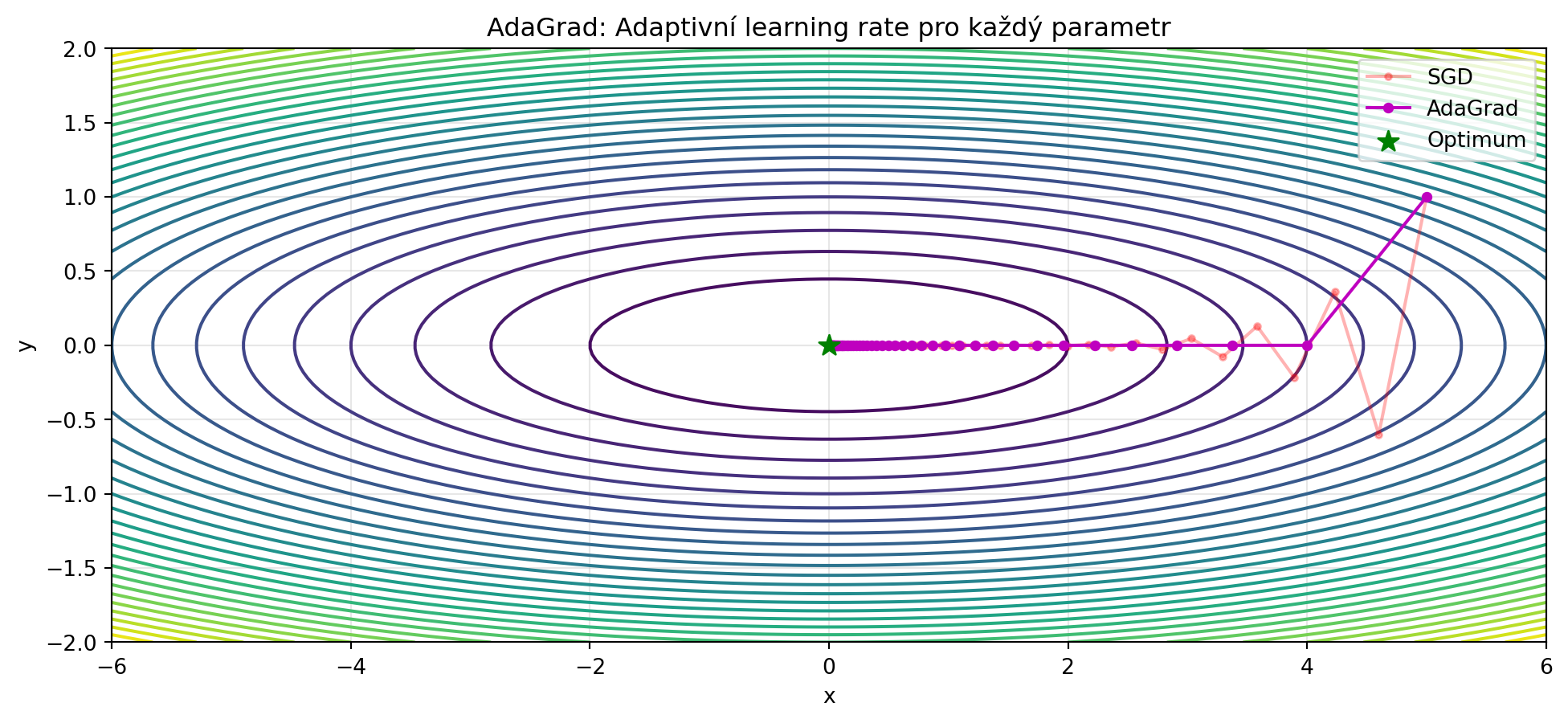
## AdaGrad: Adaptivní learning rate
**AdaGrad** přizpůsobuje learning rate pro každý parametr zvlášť - parametry s velkými gradienty mají menší learning rate:
::: {.callout-note}
## Algoritmus: AdaGrad
$$\mathbf{G}_{t+1} = \mathbf{G}_t + (\nabla f(\mathbf{w}_t))^2$$
$$\mathbf{w}_{t+1} = \mathbf{w}_t - \frac{\eta}{\sqrt{\mathbf{G}_{t+1}} + \epsilon} \nabla f(\mathbf{w}_t)$$
kde $\epsilon \approx 10^{-8}$ je pro numerickou stabilitu.
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
def adagrad(grad_f, w0, lr=0.5, eps=1e-8, n_iter=50):
"""AdaGrad optimalizátor."""
w = np.array(w0, dtype=float)
G = np.zeros_like(w)
history = [w.copy()]
for _ in range(n_iter):
grad = grad_f(w)
G = G + grad**2
w = w - lr * grad / (np.sqrt(G) + eps)
history.append(w.copy())
return np.array(history)
path_adagrad = adagrad(grad_ill, [5.0, 1.0], lr=1.0)
plt.figure(figsize=(12, 5))
plt.contour(X, Y, Z, levels=30, cmap='viridis')
plt.plot(path_sgd[:, 0], path_sgd[:, 1], 'ro-', markersize=3, alpha=0.3, label='SGD')
plt.plot(path_adagrad[:, 0], path_adagrad[:, 1], 'mo-', markersize=4, label='AdaGrad')
plt.scatter([0], [0], color='green', s=100, marker='*', zorder=5, label='Optimum')
plt.xlabel('x')
plt.ylabel('y')
plt.title('AdaGrad: Adaptivní learning rate pro každý parametr')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
print("AdaGrad automaticky upravuje learning rate!")
print("Parametry s většími gradienty mají menší learning rate.")
```
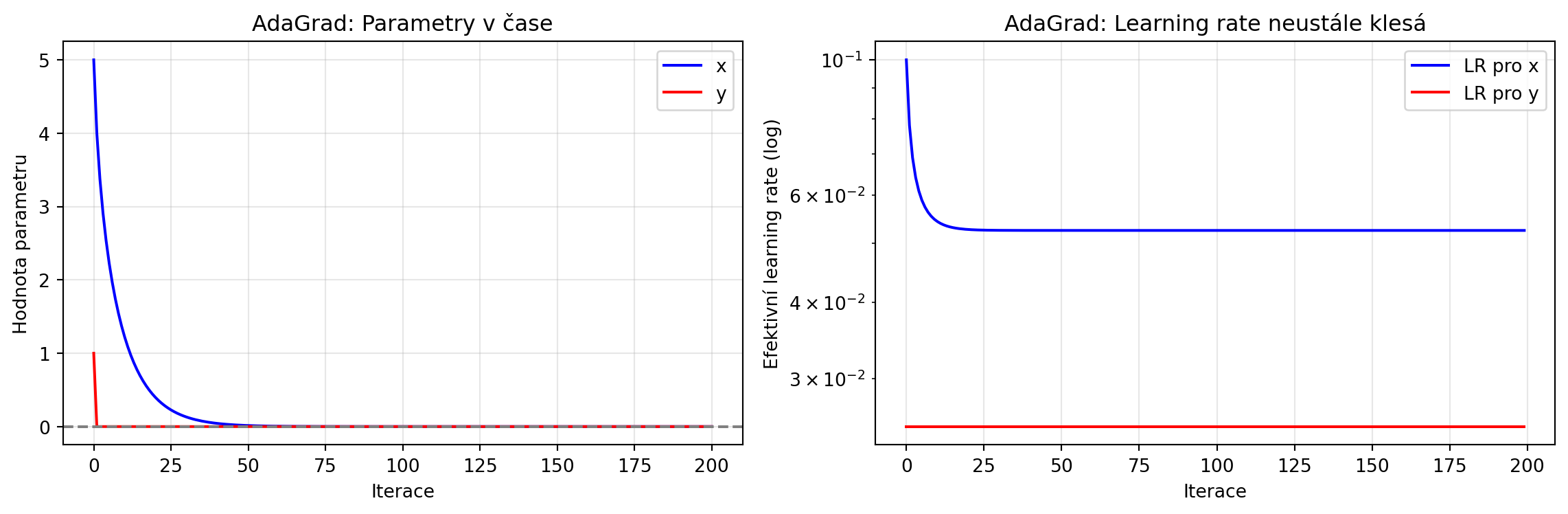
### Problém AdaGrad
AdaGrad akumuluje čtverce gradientů, takže learning rate neustále klesá a může předčasně "zmrznout":
```{python}
# Demonstrace problému
import numpy as np
import matplotlib.pyplot as plt
path_adagrad_long = adagrad(grad_ill, [5.0, 1.0], lr=1.0, n_iter=200)
# Efektivní learning rate v čase
effective_lrs = []
G = np.zeros(2)
w = np.array([5.0, 1.0])
for _ in range(200):
grad = grad_ill(w)
G = G + grad**2
eff_lr = 1.0 / (np.sqrt(G) + 1e-8)
effective_lrs.append(eff_lr.copy())
w = w - 1.0 * grad / (np.sqrt(G) + 1e-8)
effective_lrs = np.array(effective_lrs)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.plot(path_adagrad_long[:, 0], 'b-', label='x')
ax1.plot(path_adagrad_long[:, 1], 'r-', label='y')
ax1.axhline(y=0, color='gray', linestyle='--')
ax1.set_xlabel('Iterace')
ax1.set_ylabel('Hodnota parametru')
ax1.set_title('AdaGrad: Parametry v čase')
ax1.legend()
ax1.grid(True, alpha=0.3)
ax2.semilogy(effective_lrs[:, 0], 'b-', label='LR pro x')
ax2.semilogy(effective_lrs[:, 1], 'r-', label='LR pro y')
ax2.set_xlabel('Iterace')
ax2.set_ylabel('Efektivní learning rate (log)')
ax2.set_title('AdaGrad: Learning rate neustále klesá')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
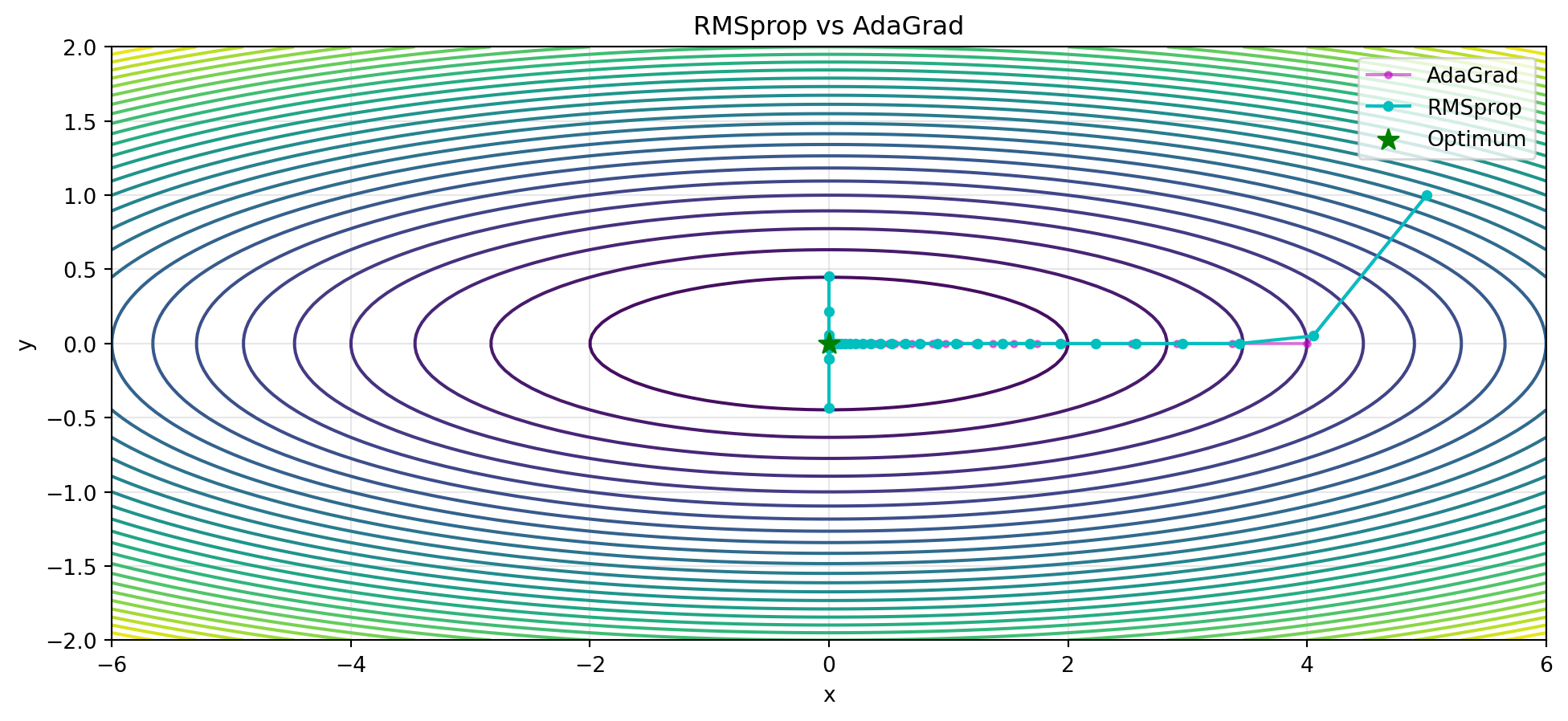
## RMSprop: Řešení problému AdaGrad
**RMSprop** používá exponenciální klouzavý průměr místo prosté akumulace:
::: {.callout-note}
## Algoritmus: RMSprop
$$\mathbf{G}_{t+1} = \beta \mathbf{G}_t + (1-\beta)(\nabla f(\mathbf{w}_t))^2$$
$$\mathbf{w}_{t+1} = \mathbf{w}_t - \frac{\eta}{\sqrt{\mathbf{G}_{t+1}} + \epsilon} \nabla f(\mathbf{w}_t)$$
Typicky $\beta = 0.9$.
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
def rmsprop(grad_f, w0, lr=0.1, beta=0.9, eps=1e-8, n_iter=50):
"""RMSprop optimalizátor."""
w = np.array(w0, dtype=float)
G = np.zeros_like(w)
history = [w.copy()]
for _ in range(n_iter):
grad = grad_f(w)
G = beta * G + (1 - beta) * grad**2
w = w - lr * grad / (np.sqrt(G) + eps)
history.append(w.copy())
return np.array(history)
path_rmsprop = rmsprop(grad_ill, [5.0, 1.0], lr=0.3, beta=0.9)
plt.figure(figsize=(12, 5))
plt.contour(X, Y, Z, levels=30, cmap='viridis')
plt.plot(path_adagrad[:, 0], path_adagrad[:, 1], 'mo-', markersize=3, alpha=0.5, label='AdaGrad')
plt.plot(path_rmsprop[:, 0], path_rmsprop[:, 1], 'co-', markersize=4, label='RMSprop')
plt.scatter([0], [0], color='green', s=100, marker='*', zorder=5, label='Optimum')
plt.xlabel('x')
plt.ylabel('y')
plt.title('RMSprop vs AdaGrad')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
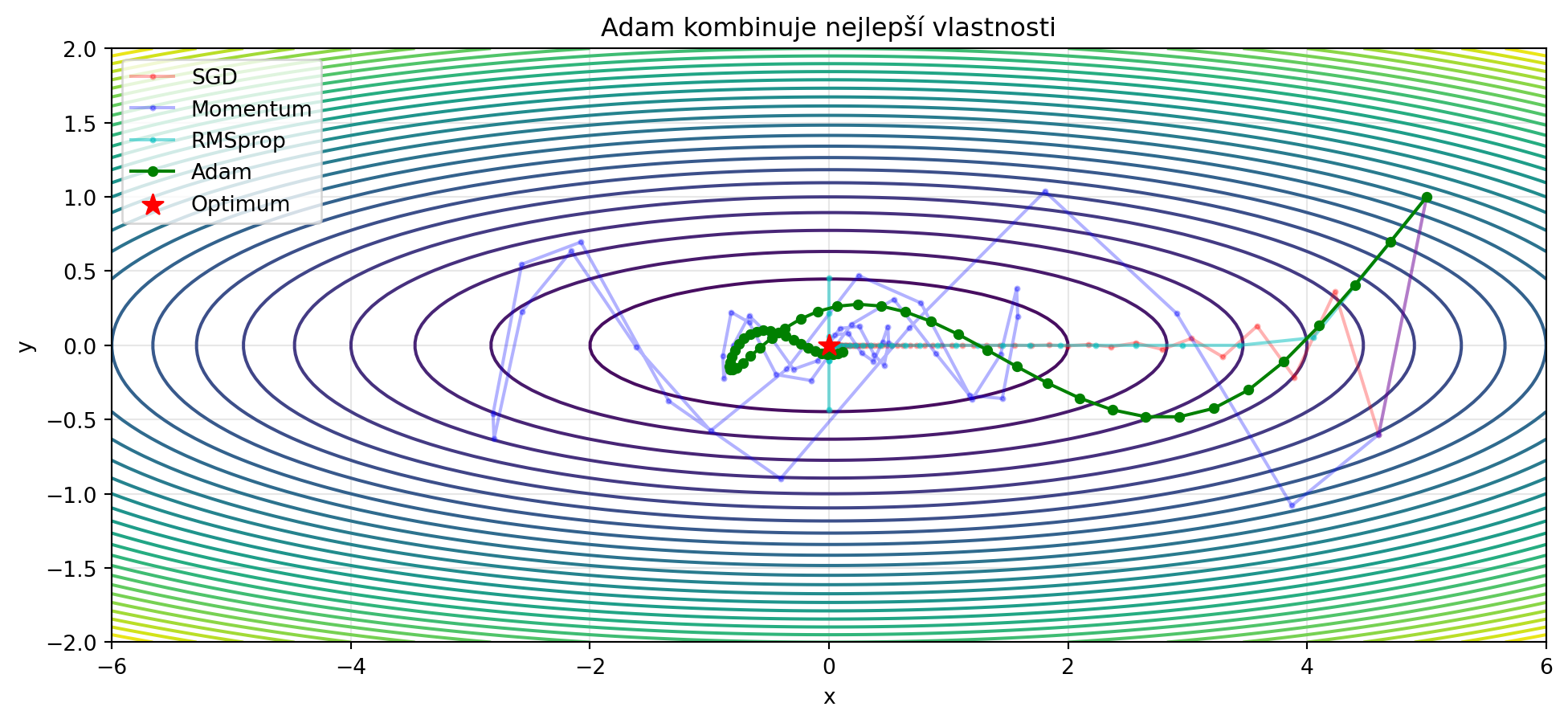
## Adam: Kombinace všeho nejlepšího
**Adam** (Adaptive Moment Estimation) kombinuje momentum a adaptivní learning rate:
::: {.callout-note}
## Algoritmus: Adam
**První moment** (momentum):
$$\mathbf{m}_{t+1} = \beta_1 \mathbf{m}_t + (1-\beta_1) \nabla f(\mathbf{w}_t)$$
**Druhý moment** (RMSprop):
$$\mathbf{v}_{t+1} = \beta_2 \mathbf{v}_t + (1-\beta_2) (\nabla f(\mathbf{w}_t))^2$$
**Korekce zkreslení**:
$$\hat{\mathbf{m}} = \frac{\mathbf{m}_{t+1}}{1 - \beta_1^{t+1}}, \quad \hat{\mathbf{v}} = \frac{\mathbf{v}_{t+1}}{1 - \beta_2^{t+1}}$$
**Update**:
$$\mathbf{w}_{t+1} = \mathbf{w}_t - \eta \frac{\hat{\mathbf{m}}}{\sqrt{\hat{\mathbf{v}}} + \epsilon}$$
Typicky: $\beta_1 = 0.9$, $\beta_2 = 0.999$, $\epsilon = 10^{-8}$
:::
```{python}
import numpy as np
import matplotlib.pyplot as plt
def adam(grad_f, w0, lr=0.1, beta1=0.9, beta2=0.999, eps=1e-8, n_iter=50):
"""Adam optimalizátor."""
w = np.array(w0, dtype=float)
m = np.zeros_like(w)
v = np.zeros_like(w)
history = [w.copy()]
for t in range(1, n_iter + 1):
grad = grad_f(w)
# Update momentů
m = beta1 * m + (1 - beta1) * grad
v = beta2 * v + (1 - beta2) * grad**2
# Korekce zkreslení
m_hat = m / (1 - beta1**t)
v_hat = v / (1 - beta2**t)
# Update parametrů
w = w - lr * m_hat / (np.sqrt(v_hat) + eps)
history.append(w.copy())
return np.array(history)
path_adam = adam(grad_ill, [5.0, 1.0], lr=0.3)
plt.figure(figsize=(12, 5))
plt.contour(X, Y, Z, levels=30, cmap='viridis')
plt.plot(path_sgd[:, 0], path_sgd[:, 1], 'ro-', markersize=2, alpha=0.3, label='SGD')
plt.plot(path_momentum[:, 0], path_momentum[:, 1], 'bo-', markersize=2, alpha=0.3, label='Momentum')
plt.plot(path_rmsprop[:, 0], path_rmsprop[:, 1], 'co-', markersize=2, alpha=0.5, label='RMSprop')
plt.plot(path_adam[:, 0], path_adam[:, 1], 'go-', markersize=4, label='Adam')
plt.scatter([0], [0], color='red', s=100, marker='*', zorder=5, label='Optimum')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Adam kombinuje nejlepší vlastnosti')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
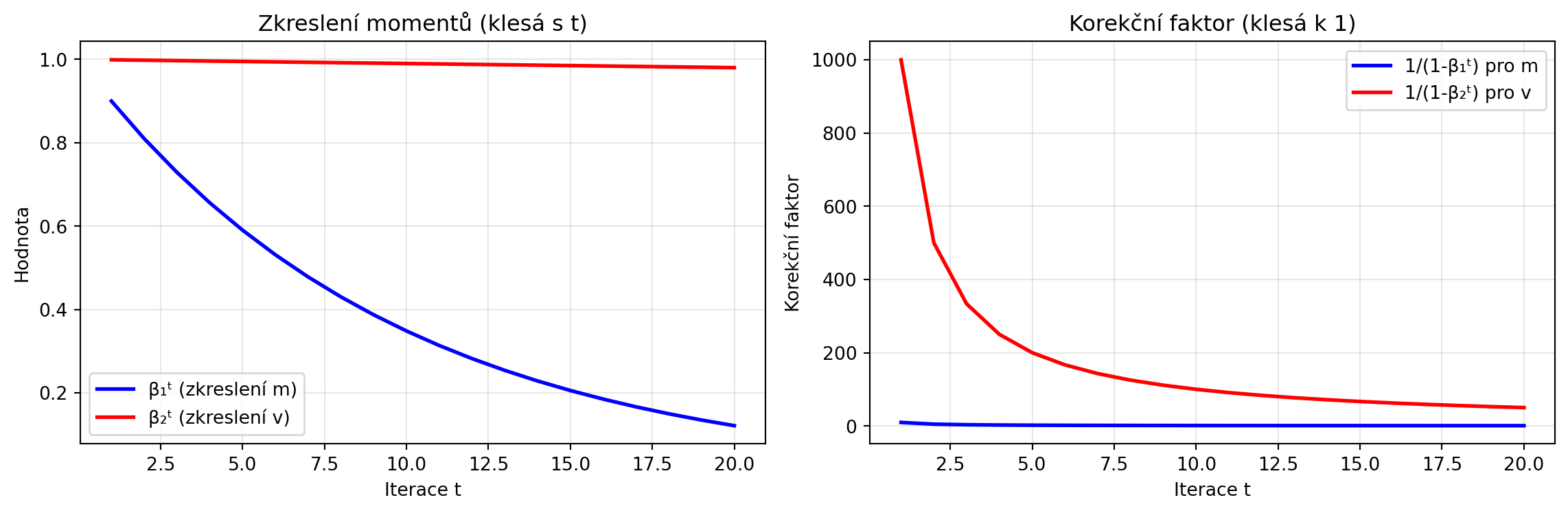
### Proč korekce zkreslení?
Na začátku jsou momenty inicializovány na nulu, což způsobuje zkreslení. Korekce to napravuje:
```{python}
# Demonstrace korekce zkreslení
import matplotlib.pyplot as plt
beta1, beta2 = 0.9, 0.999
steps = 20
# Bez korekce
bias_m = [beta1**t for t in range(1, steps+1)]
bias_v = [beta2**t for t in range(1, steps+1)]
# S korekcí (faktor, kterým se násobí)
correction_m = [1 / (1 - beta1**t) for t in range(1, steps+1)]
correction_v = [1 / (1 - beta2**t) for t in range(1, steps+1)]
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.plot(range(1, steps+1), bias_m, 'b-', label='β₁ᵗ (zkreslení m)', lw=2)
ax1.plot(range(1, steps+1), bias_v, 'r-', label='β₂ᵗ (zkreslení v)', lw=2)
ax1.set_xlabel('Iterace t')
ax1.set_ylabel('Hodnota')
ax1.set_title('Zkreslení momentů (klesá s t)')
ax1.legend()
ax1.grid(True, alpha=0.3)
ax2.plot(range(1, steps+1), correction_m, 'b-', label='1/(1-β₁ᵗ) pro m', lw=2)
ax2.plot(range(1, steps+1), correction_v, 'r-', label='1/(1-β₂ᵗ) pro v', lw=2)
ax2.set_xlabel('Iterace t')
ax2.set_ylabel('Korekční faktor')
ax2.set_title('Korekční faktor (klesá k 1)')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
## AdamW: Adam s Weight Decay
**AdamW** odděluje regularizaci od adaptivního learning rate:
::: {.callout-note}
## Adam vs AdamW
**Adam s L2 regularizací**:
$$\mathbf{w}_{t+1} = \mathbf{w}_t - \eta \frac{\hat{\mathbf{m}}}{\sqrt{\hat{\mathbf{v}}} + \epsilon}$$
kde gradient zahrnuje $\lambda \mathbf{w}$ (L2 regularizace)
**AdamW** (decoupled weight decay):
$$\mathbf{w}_{t+1} = \mathbf{w}_t - \eta \frac{\hat{\mathbf{m}}}{\sqrt{\hat{\mathbf{v}}} + \epsilon} - \eta \lambda \mathbf{w}_t$$
AdamW funguje lépe v praxi!
:::
```{python}
import numpy as np
def adamw(grad_f, w0, lr=0.1, beta1=0.9, beta2=0.999, eps=1e-8, weight_decay=0.01, n_iter=50):
"""AdamW optimalizátor."""
w = np.array(w0, dtype=float)
m = np.zeros_like(w)
v = np.zeros_like(w)
history = [w.copy()]
for t in range(1, n_iter + 1):
grad = grad_f(w)
# Update momentů
m = beta1 * m + (1 - beta1) * grad
v = beta2 * v + (1 - beta2) * grad**2
# Korekce zkreslení
m_hat = m / (1 - beta1**t)
v_hat = v / (1 - beta2**t)
# Update s weight decay
w = w - lr * m_hat / (np.sqrt(v_hat) + eps) - lr * weight_decay * w
history.append(w.copy())
return np.array(history)
print("AdamW je dnes standardní volba pro trénink transformerů!")
```
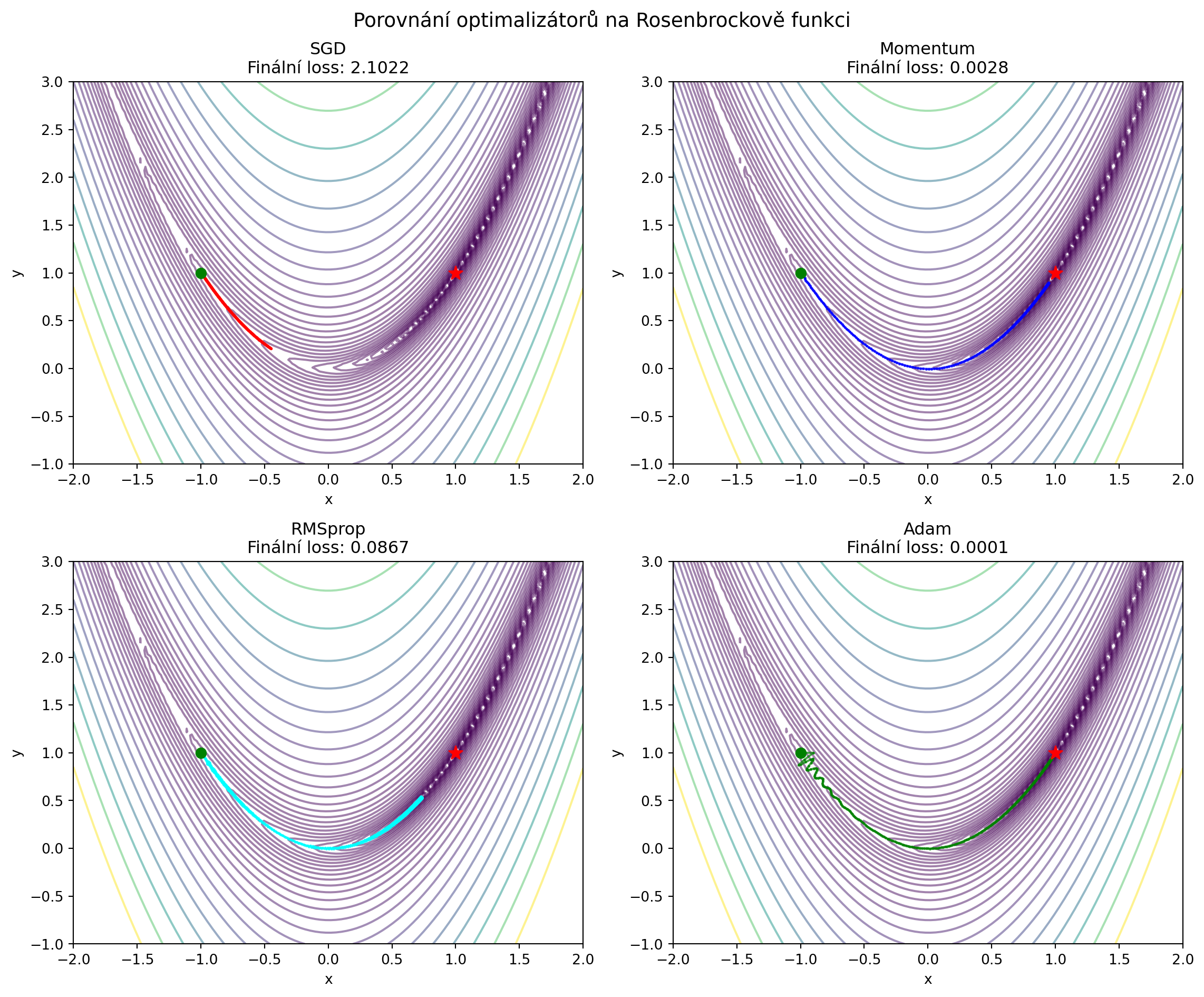
## Porovnání optimalizátorů
```{python}
# Rosenbrockova funkce - náročný test
import numpy as np
import matplotlib.pyplot as plt
def rosenbrock(pos):
x, y = pos
return (1 - x)**2 + 100 * (y - x**2)**2
def grad_rosenbrock(pos):
x, y = pos
dx = -2 * (1 - x) + 200 * (y - x**2) * (-2 * x)
dy = 200 * (y - x**2)
return np.array([dx, dy])
start = np.array([-1.0, 1.0])
n_iter = 500
paths = {
'SGD': [],
'Momentum': [],
'RMSprop': [],
'Adam': []
}
# SGD
w = start.copy()
for _ in range(n_iter):
paths['SGD'].append(w.copy())
w = w - 0.001 * grad_rosenbrock(w)
# Momentum
w = start.copy()
v = np.zeros(2)
for _ in range(n_iter):
paths['Momentum'].append(w.copy())
v = 0.9 * v + grad_rosenbrock(w)
w = w - 0.001 * v
# RMSprop
w = start.copy()
G = np.zeros(2)
for _ in range(n_iter):
paths['RMSprop'].append(w.copy())
grad = grad_rosenbrock(w)
G = 0.9 * G + 0.1 * grad**2
w = w - 0.01 * grad / (np.sqrt(G) + 1e-8)
# Adam
paths['Adam'] = adam(grad_rosenbrock, start, lr=0.1, n_iter=n_iter).tolist()
# Vizualizace
x = np.linspace(-2, 2, 100)
y = np.linspace(-1, 3, 100)
X, Y = np.meshgrid(x, y)
Z = rosenbrock([X, Y])
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
colors = {'SGD': 'red', 'Momentum': 'blue', 'RMSprop': 'cyan', 'Adam': 'green'}
for ax, (name, path) in zip(axes.flatten(), paths.items()):
path = np.array(path)
ax.contour(X, Y, Z, levels=np.logspace(-1, 3, 30), cmap='viridis', alpha=0.5)
ax.plot(path[:, 0], path[:, 1], 'o-', color=colors[name], markersize=1, alpha=0.7)
ax.scatter([1], [1], color='red', s=100, marker='*', zorder=5)
ax.scatter([path[0, 0]], [path[0, 1]], color='green', s=50, zorder=5)
final_loss = rosenbrock(path[-1])
ax.set_title(f'{name}\nFinální loss: {final_loss:.4f}')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(-2, 2)
ax.set_ylim(-1, 3)
plt.suptitle('Porovnání optimalizátorů na Rosenbrockově funkci', fontsize=14)
plt.tight_layout()
plt.show()
```
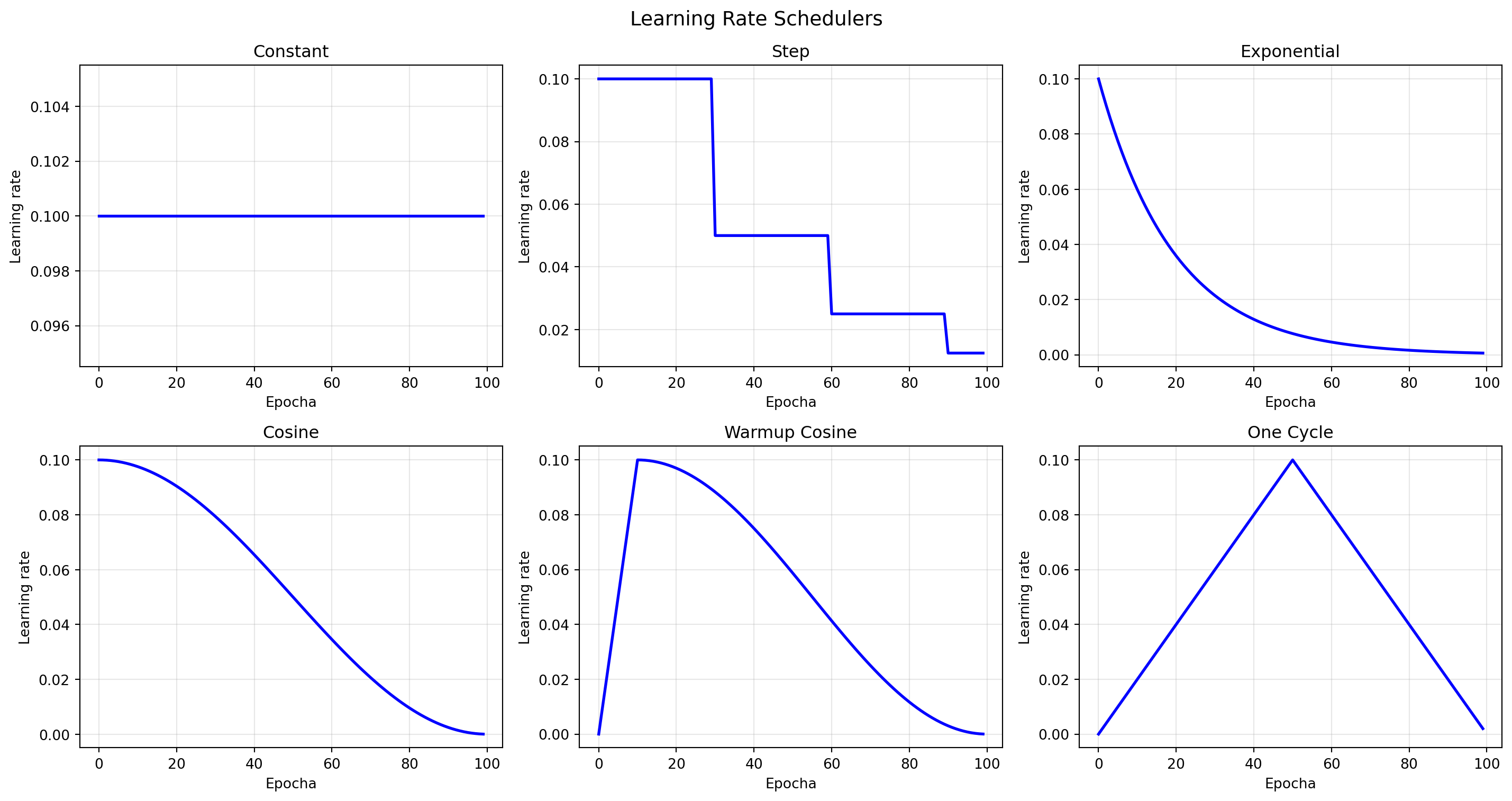
## Learning Rate Scheduling
Měnění learning rate během tréninku může výrazně zlepšit výsledky:
```{python}
import numpy as np
import matplotlib.pyplot as plt
def train_with_scheduler(scheduler_type, initial_lr=0.1, n_epochs=100):
"""Simulace tréninku s různými schedulery."""
lrs = []
for epoch in range(n_epochs):
if scheduler_type == 'constant':
lr = initial_lr
elif scheduler_type == 'step':
# Sníží LR na polovinu každých 30 epoch
lr = initial_lr * (0.5 ** (epoch // 30))
elif scheduler_type == 'exponential':
lr = initial_lr * (0.95 ** epoch)
elif scheduler_type == 'cosine':
lr = initial_lr * 0.5 * (1 + np.cos(np.pi * epoch / n_epochs))
elif scheduler_type == 'warmup_cosine':
warmup_epochs = 10
if epoch < warmup_epochs:
lr = initial_lr * epoch / warmup_epochs
else:
progress = (epoch - warmup_epochs) / (n_epochs - warmup_epochs)
lr = initial_lr * 0.5 * (1 + np.cos(np.pi * progress))
elif scheduler_type == 'one_cycle':
# Jednoduché one cycle
mid = n_epochs // 2
if epoch < mid:
lr = initial_lr * epoch / mid
else:
lr = initial_lr * (n_epochs - epoch) / mid
lrs.append(lr)
return lrs
schedulers = ['constant', 'step', 'exponential', 'cosine', 'warmup_cosine', 'one_cycle']
fig, axes = plt.subplots(2, 3, figsize=(15, 8))
for ax, sched in zip(axes.flatten(), schedulers):
lrs = train_with_scheduler(sched)
ax.plot(lrs, 'b-', lw=2)
ax.set_xlabel('Epocha')
ax.set_ylabel('Learning rate')
ax.set_title(sched.replace('_', ' ').title())
ax.grid(True, alpha=0.3)
plt.suptitle('Learning Rate Schedulers', fontsize=14)
plt.tight_layout()
plt.show()
```
## PyTorch optimalizátory
```{python}
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
# Vytvoření modelu
torch.manual_seed(42)
model = nn.Sequential(
nn.Linear(10, 32),
nn.ReLU(),
nn.Linear(32, 1)
)
# Data
X = torch.randn(100, 10)
y = torch.randn(100, 1)
# Různé optimalizátory
optimizers = {
'SGD': optim.SGD(model.parameters(), lr=0.01),
'SGD+Momentum': optim.SGD(model.parameters(), lr=0.01, momentum=0.9),
'RMSprop': optim.RMSprop(model.parameters(), lr=0.01),
'Adam': optim.Adam(model.parameters(), lr=0.01),
'AdamW': optim.AdamW(model.parameters(), lr=0.01, weight_decay=0.01),
}
print("PyTorch optimalizátory:")
for name, opt in optimizers.items():
print(f" {name}: {type(opt).__name__}")
# Příklad tréninku
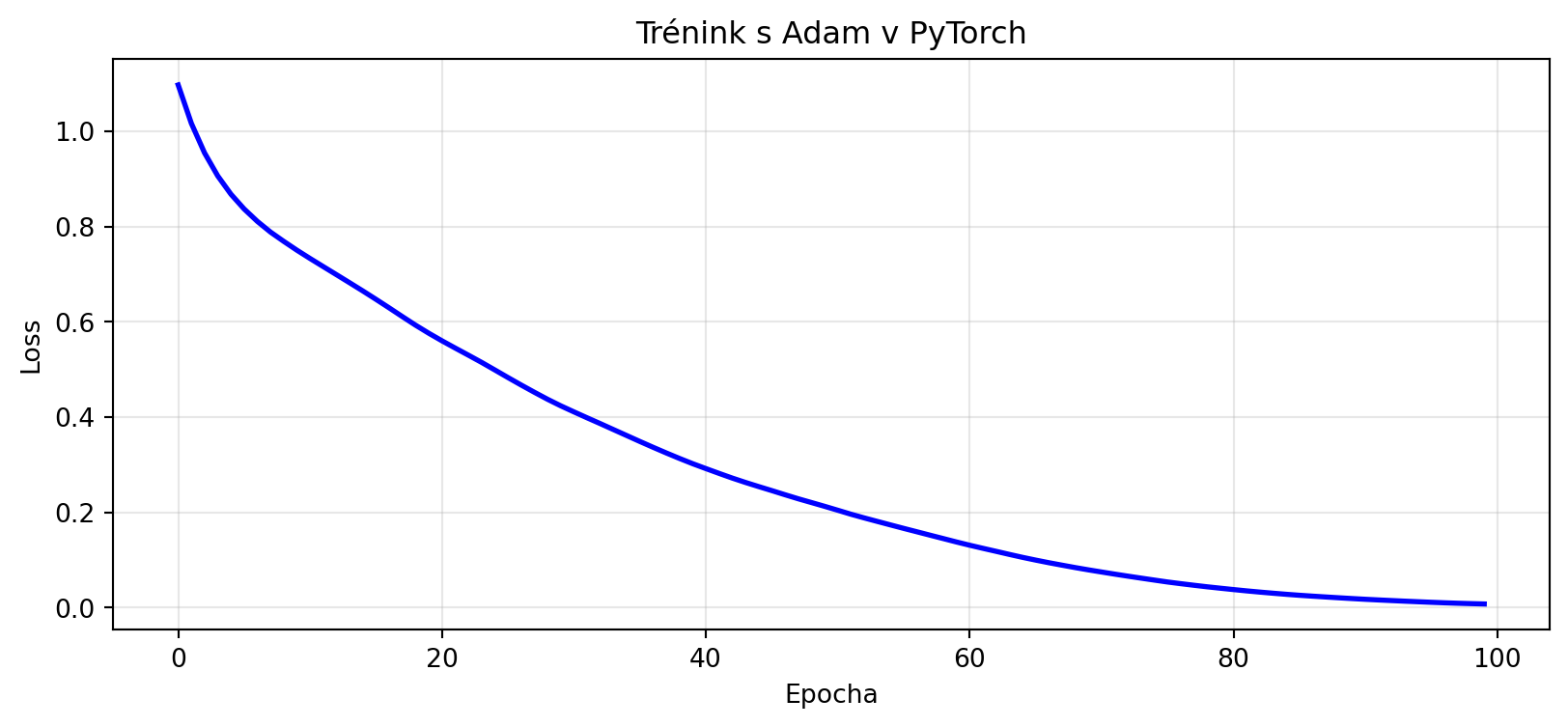
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
losses = []
for epoch in range(100):
optimizer.zero_grad()
output = model(X)
loss = criterion(output, y)
loss.backward()
optimizer.step()
losses.append(loss.item())
plt.figure(figsize=(10, 4))
plt.plot(losses, 'b-', lw=2)
plt.xlabel('Epocha')
plt.ylabel('Loss')
plt.title('Trénink s Adam v PyTorch')
plt.grid(True, alpha=0.3)
plt.show()
```
### Learning Rate Scheduler v PyTorch
```{python}
# Reset modelu
import matplotlib.pyplot as plt
for layer in model:
if hasattr(layer, 'reset_parameters'):
layer.reset_parameters()
optimizer = optim.Adam(model.parameters(), lr=0.1)
scheduler = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=100)
losses = []
lrs = []
for epoch in range(100):
lrs.append(optimizer.param_groups[0]['lr'])
optimizer.zero_grad()
output = model(X)
loss = criterion(output, y)
loss.backward()
optimizer.step()
scheduler.step()
losses.append(loss.item())
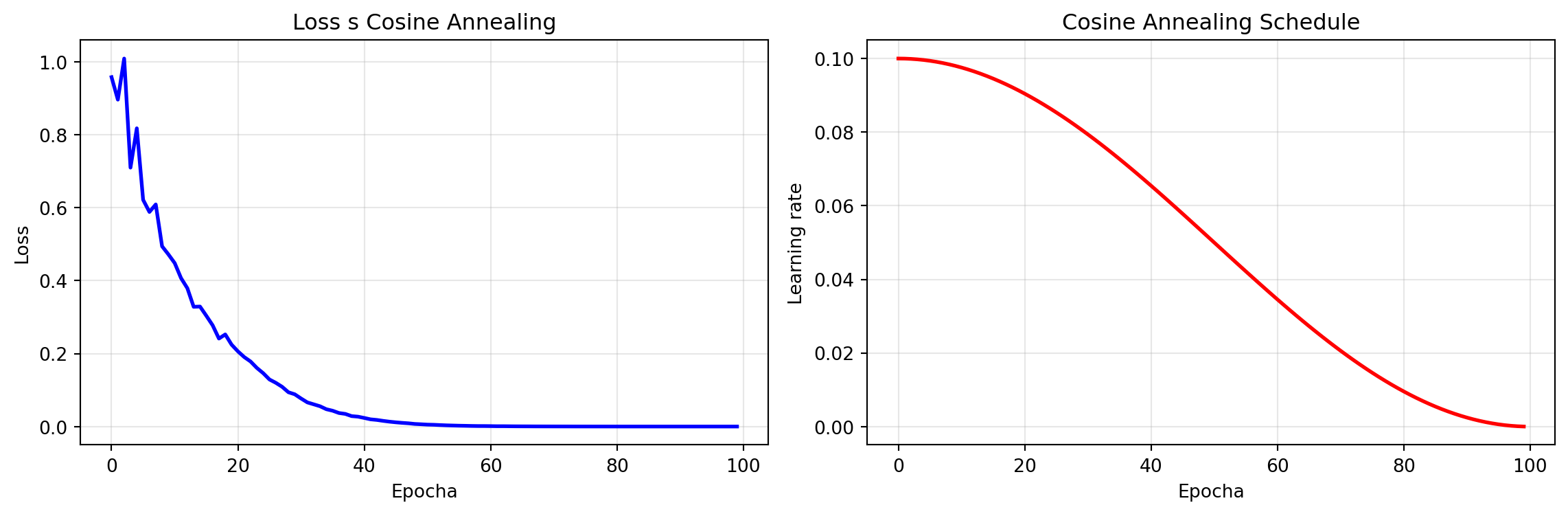
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.plot(losses, 'b-', lw=2)
ax1.set_xlabel('Epocha')
ax1.set_ylabel('Loss')
ax1.set_title('Loss s Cosine Annealing')
ax1.grid(True, alpha=0.3)
ax2.plot(lrs, 'r-', lw=2)
ax2.set_xlabel('Epocha')
ax2.set_ylabel('Learning rate')
ax2.set_title('Cosine Annealing Schedule')
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
```
## Řešené příklady
### Příklad 1: Porovnání konvergence
**Zadání**: Porovnejte rychlost konvergence různých optimalizátorů na jednoduché kvadratické funkci.
**Řešení**:
```{python}
import numpy as np
import matplotlib.pyplot as plt
def quadratic(pos):
return pos[0]**2 + 10*pos[1]**2
def grad_quadratic(pos):
return np.array([2*pos[0], 20*pos[1]])
start = np.array([5.0, 2.0])
n_iter = 100
results = {}
# SGD
w = start.copy()
losses = [quadratic(w)]
for _ in range(n_iter):
w = w - 0.05 * grad_quadratic(w)
losses.append(quadratic(w))
results['SGD'] = losses
# Momentum
w = start.copy()
v = np.zeros(2)
losses = [quadratic(w)]
for _ in range(n_iter):
v = 0.9 * v + grad_quadratic(w)
w = w - 0.05 * v
losses.append(quadratic(w))
results['Momentum'] = losses
# Adam
losses = [quadratic(start)]
path = adam(grad_quadratic, start, lr=0.5, n_iter=n_iter)
for p in path[1:]:
losses.append(quadratic(p))
results['Adam'] = losses
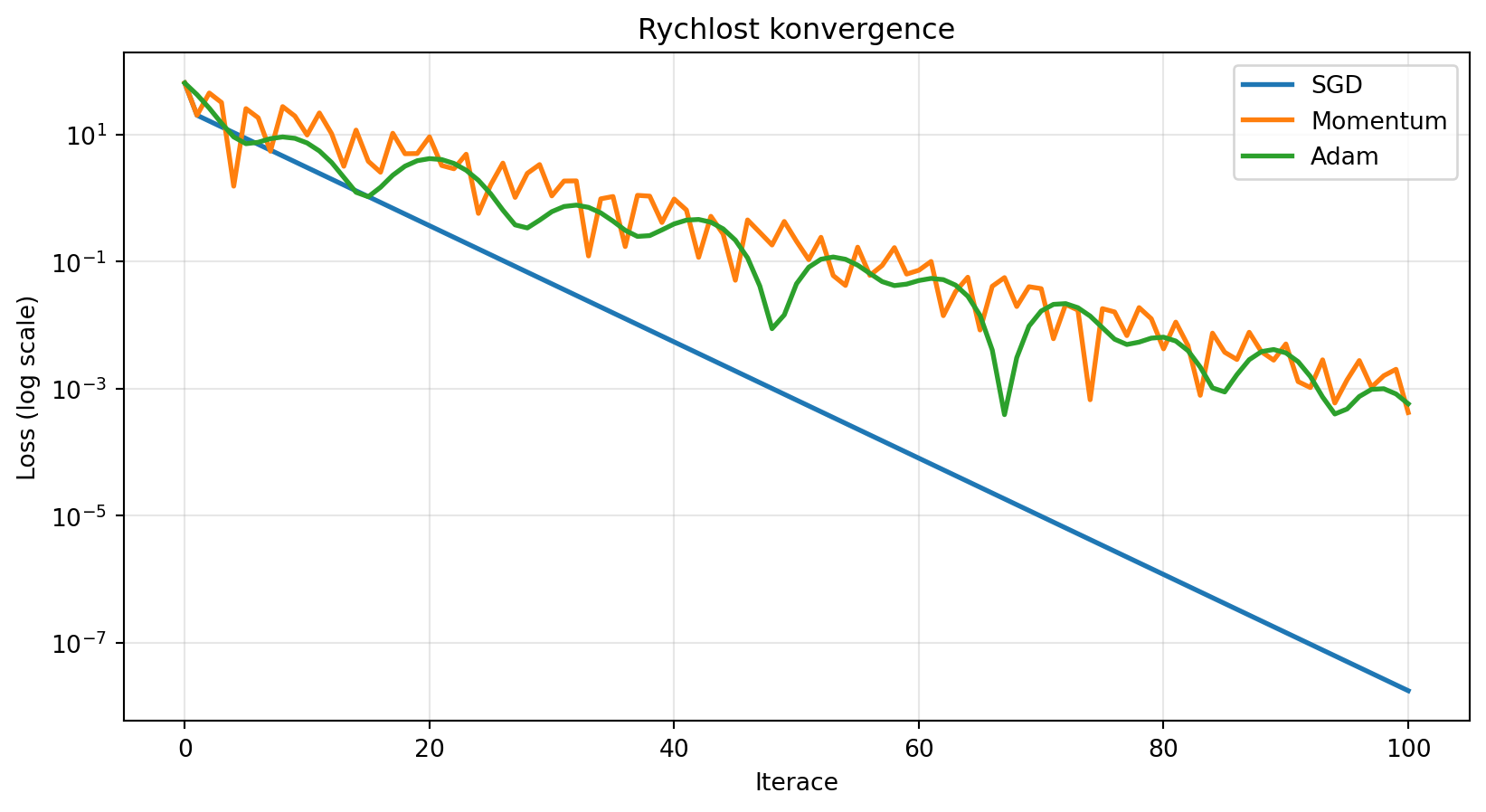
plt.figure(figsize=(10, 5))
for name, losses in results.items():
plt.semilogy(losses, label=name, lw=2)
plt.xlabel('Iterace')
plt.ylabel('Loss (log scale)')
plt.title('Rychlost konvergence')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
```
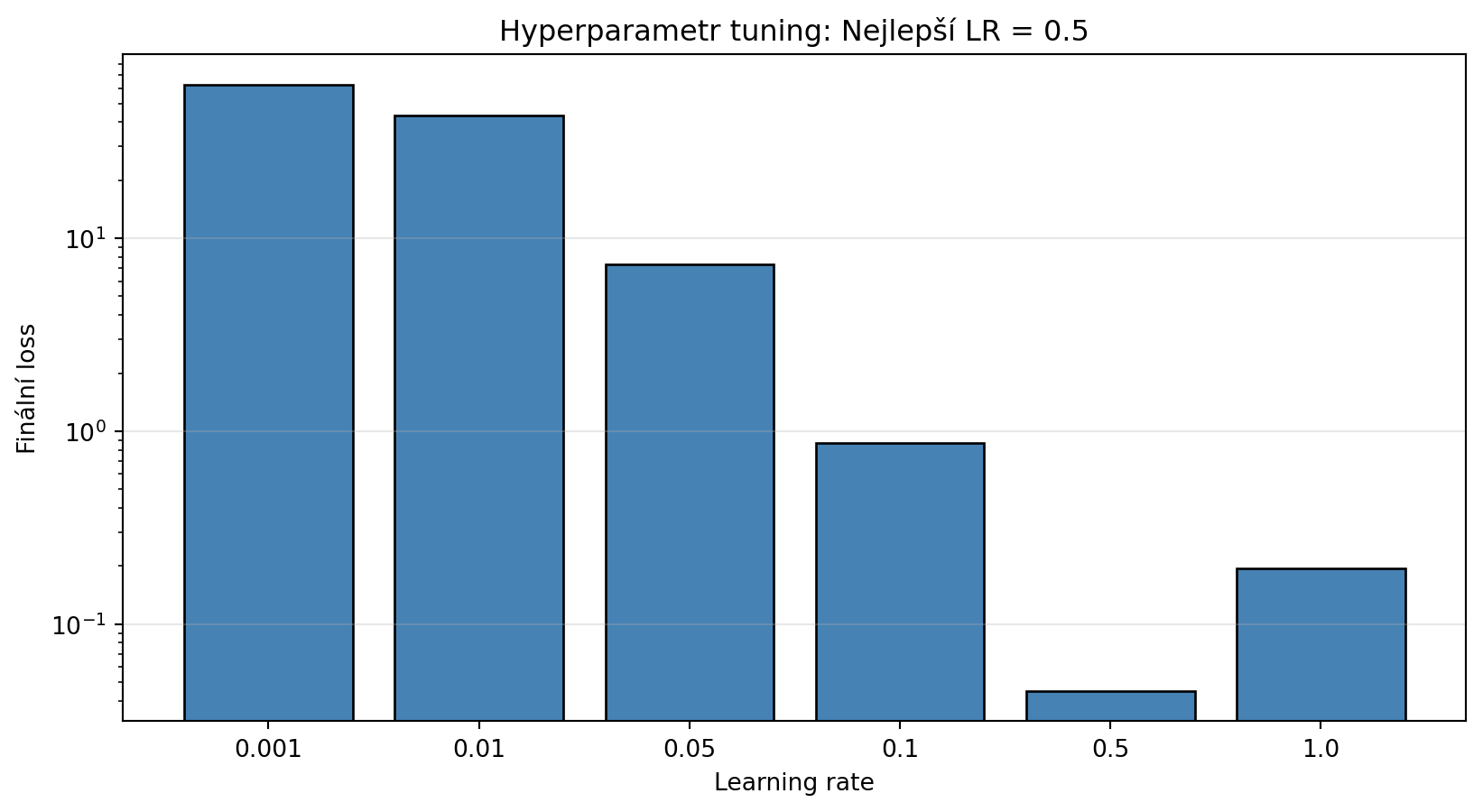
### Příklad 2: Hyperparametr tuning
**Zadání**: Najděte optimální learning rate pro Adam na dané úloze.
**Řešení**:
```{python}
import matplotlib.pyplot as plt
def find_best_lr(grad_f, start, lr_range, n_iter=50):
"""Najde nejlepší learning rate."""
best_lr = None
best_final_loss = float('inf')
results = {}
for lr in lr_range:
path = adam(grad_f, start, lr=lr, n_iter=n_iter)
final_loss = quadratic(path[-1])
results[lr] = final_loss
if final_loss < best_final_loss:
best_final_loss = final_loss
best_lr = lr
return best_lr, results
lr_range = [0.001, 0.01, 0.05, 0.1, 0.5, 1.0]
best_lr, results = find_best_lr(grad_quadratic, [5.0, 2.0], lr_range)
plt.figure(figsize=(10, 5))
plt.bar([str(lr) for lr in results.keys()], list(results.values()), color='steelblue', edgecolor='black')
plt.xlabel('Learning rate')
plt.ylabel('Finální loss')
plt.title(f'Hyperparametr tuning: Nejlepší LR = {best_lr}')
plt.yscale('log')
plt.grid(axis='y', alpha=0.3)
plt.show()
```
### Příklad 3: Implementace vlastního optimalizátoru v PyTorch
**Zadání**: Implementujte vlastní optimalizátor jako podtřídu `torch.optim.Optimizer`.
**Řešení**:
```{python}
class CustomSGDMomentum(optim.Optimizer):
"""Vlastní implementace SGD s momentum."""
def __init__(self, params, lr=0.01, momentum=0.9):
defaults = dict(lr=lr, momentum=momentum)
super().__init__(params, defaults)
def step(self):
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
d_p = p.grad.data
# Inicializace velocity
state = self.state[p]
if 'velocity' not in state:
state['velocity'] = torch.zeros_like(p.data)
v = state['velocity']
v.mul_(group['momentum']).add_(d_p)
p.data.add_(v, alpha=-group['lr'])
# Test
torch.manual_seed(42)
model = nn.Linear(10, 1)
X = torch.randn(100, 10)
y = torch.randn(100, 1)
optimizer = CustomSGDMomentum(model.parameters(), lr=0.01, momentum=0.9)
criterion = nn.MSELoss()
losses = []
for _ in range(50):
optimizer.zero_grad()
loss = criterion(model(X), y)
loss.backward()
optimizer.step()
losses.append(loss.item())
print(f"Finální loss s vlastním optimalizátorem: {losses[-1]:.4f}")
```
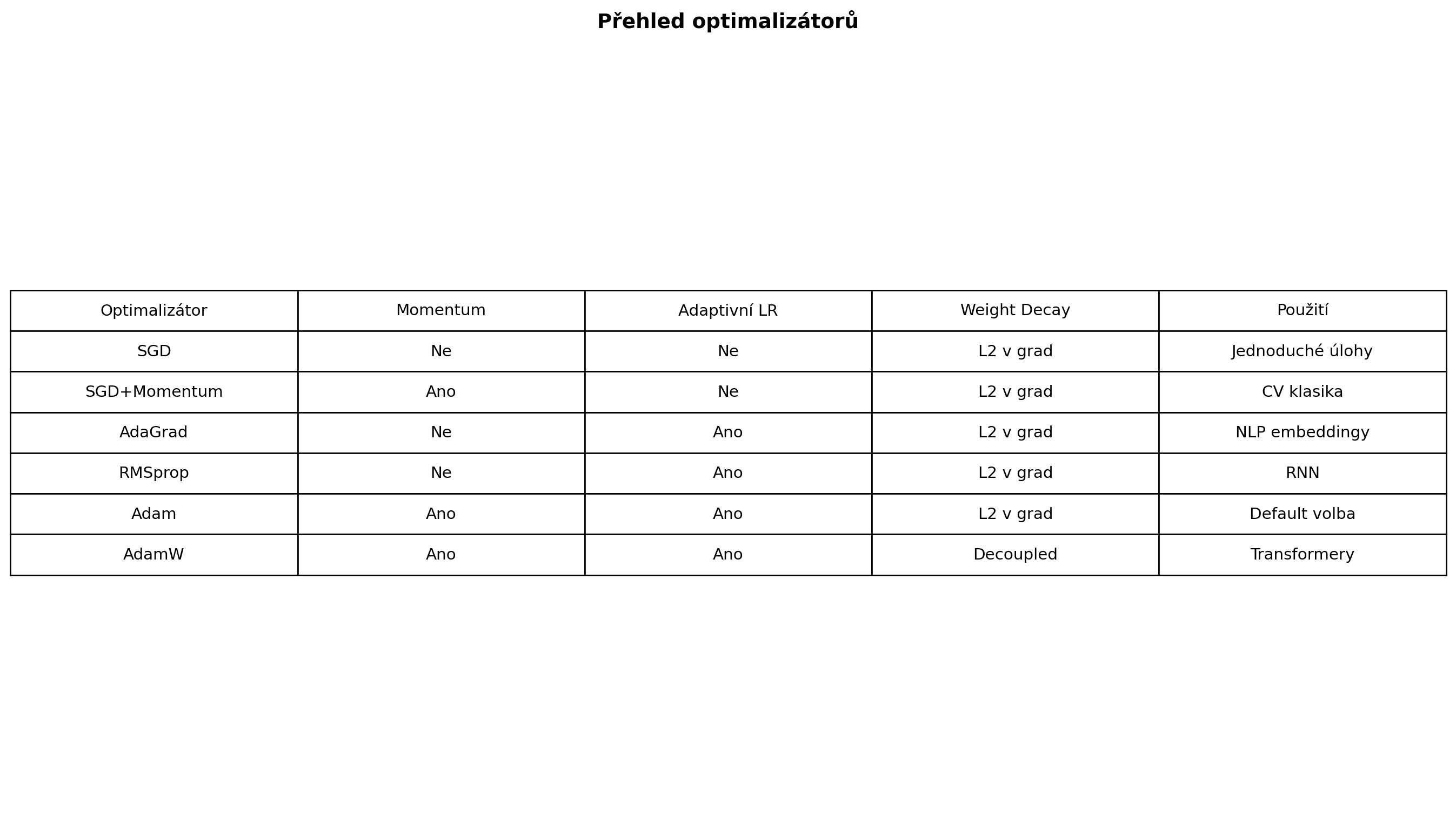
## Shrnutí optimalizátorů
```{python}
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(14, 8))
data = {
'Optimalizátor': ['SGD', 'SGD+Momentum', 'AdaGrad', 'RMSprop', 'Adam', 'AdamW'],
'Momentum': ['Ne', 'Ano', 'Ne', 'Ne', 'Ano', 'Ano'],
'Adaptivní LR': ['Ne', 'Ne', 'Ano', 'Ano', 'Ano', 'Ano'],
'Weight Decay': ['L2 v grad', 'L2 v grad', 'L2 v grad', 'L2 v grad', 'L2 v grad', 'Decoupled'],
'Použití': ['Jednoduché úlohy', 'CV klasika', 'NLP embeddingy', 'RNN', 'Default volba', 'Transformery']
}
# Tabulka jako text
ax.axis('off')
table = ax.table(
cellText=[list(row) for row in zip(*data.values())],
colLabels=list(data.keys()),
loc='center',
cellLoc='center'
)
table.auto_set_font_size(False)
table.set_fontsize(11)
table.scale(1.2, 2)
plt.title('Přehled optimalizátorů', fontsize=14, fontweight='bold', pad=20)
plt.tight_layout()
plt.show()
```
## Cvičení
::: {.callout-note icon=false}
## Cvičení 1: Implementace
Implementujte Nesterov Accelerated Gradient od nuly a porovnejte s klasickým momentum.
:::
::: {.callout-note icon=false}
## Cvičení 2: Hyperparametry Adam
Experimentujte s hyperparametry Adam ($\beta_1$, $\beta_2$) na Rosenbrockově funkci. Které hodnoty fungují nejlépe?
:::
::: {.callout-note icon=false}
## Cvičení 3: Warmup
Implementujte learning rate warmup pro Adam a ukažte, že pomáhá stabilitě na začátku tréninku.
:::
::: {.callout-note icon=false}
## Cvičení 4: MNIST
Natrénujte jednoduchou neuronovou síť na MNIST s různými optimalizátory. Porovnejte rychlost konvergence a finální přesnost.
:::
::: {.callout-note icon=false}
## Cvičení 5: Gradient accumulation
Implementujte gradient accumulation - techniku, která umožňuje efektivně zvětšit batch size bez zvýšení paměťových nároků.
:::
## Shrnutí
::: {.callout-tip}
## Co jsme se naučili
1. **Momentum** přidává setrvačnost a tlumí oscilace
2. **AdaGrad** adaptuje learning rate pro každý parametr
3. **RMSprop** řeší problém klesajícího LR v AdaGrad
4. **Adam** kombinuje momentum a adaptivní LR - nejpoužívanější optimalizátor
5. **AdamW** správně implementuje weight decay - standard pro transformery
6. **LR scheduling** mění learning rate během tréninku pro lepší výsledky
:::
::: {.callout-important}
## Praktická doporučení
1. **Výchozí volba**: Adam nebo AdamW s LR ~ 0.001
2. **Pro transformery**: AdamW s warmup + cosine decay
3. **Pro CNN**: SGD s momentum může dosáhnout lepších výsledků
4. **Vždy experimentujte** s learning rate - je to nejdůležitější hyperparametr
5. **Používejte LR scheduling** pro dosažení nejlepších výsledků
:::
Tímto končíme část o optimalizaci. V další části se konečně podíváme na praktické neuronové sítě a jak všechny tyto koncepty spojit dohromady.