# Vektory -- šipky v prostoru
::: {.callout-tip title="Co se naučíte"}
V této kapitole se naučíte:
- Co je vektor a jak ho reprezentovat
- Rozdíl mezi skalárem a vektorem
- Geometrickou interpretaci vektorů
- Jak vypočítat délku (normu) vektoru
- Pracovat s vektory v NumPy
:::
## Proč potřebujeme vektory?
V předchozích kapitolách jsme pracovali s jednotlivými čísly. Ale v reálném světě často potřebujeme popsat něco, co má více vlastností najednou:
- **Pozice** má souřadnice x a y (nebo x, y, z ve 3D)
- **Rychlost** má směr a velikost
- **Barva** na obrazovce má složky R, G, B
- **Slovo** v jazykovém modelu je reprezentováno stovkami čísel (embedding)
Pro všechny tyto případy používáme **vektory**.
::: {.callout-note title="Vektory v AI"}
V neuronových sítích a jazykových modelech jsou vektory všudypřítomné:
- Každé slovo je reprezentováno jako vektor (word embedding)
- Vstupy a výstupy neuronů jsou vektory
- Obrázky jsou reprezentovány jako vektory pixelů
:::
## Co je vektor?
**Vektor** je uspořádaná n-tice čísel. Můžeme si ho představit jako:
1. **Seznam čísel** -- matematicky
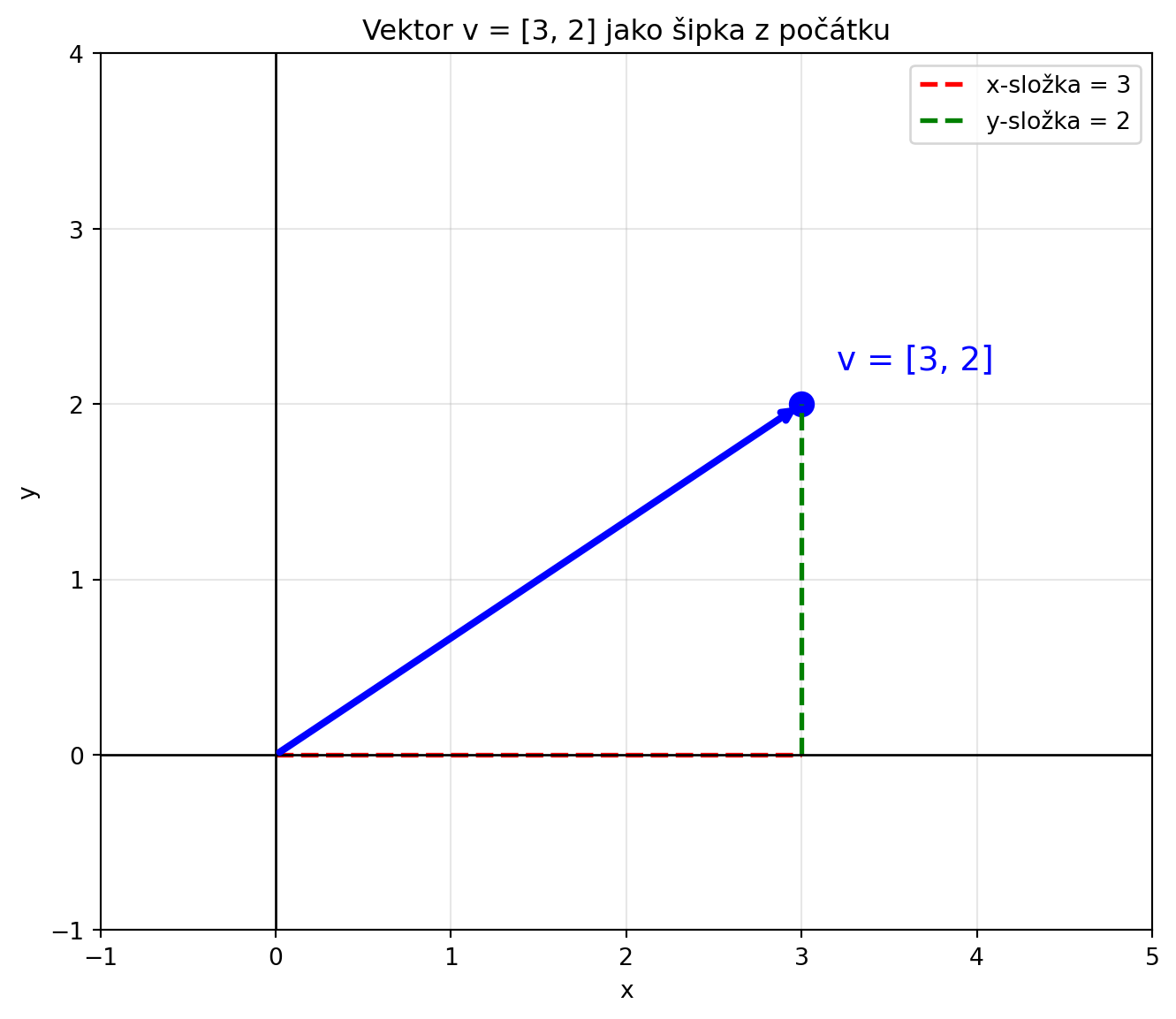
2. **Šipku v prostoru** -- geometricky
3. **Bod v prostoru** -- pozice
```{python}
#| fig-cap: "Vektor jako šipka"
#| code-fold: true
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 8))
# Vektor v = [3, 2]
ax.annotate('', xy=(3, 2), xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='blue', lw=3))
ax.plot(3, 2, 'bo', markersize=10)
ax.text(3.2, 2.2, 'v = [3, 2]', fontsize=14, color='blue')
# Složky vektoru
ax.plot([0, 3], [0, 0], 'r--', linewidth=2, label='x-složka = 3')
ax.plot([3, 3], [0, 2], 'g--', linewidth=2, label='y-složka = 2')
ax.axhline(y=0, color='k', linewidth=1)
ax.axvline(x=0, color='k', linewidth=1)
ax.grid(True, alpha=0.3)
ax.set_xlim(-1, 5)
ax.set_ylim(-1, 4)
ax.set_aspect('equal')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Vektor v = [3, 2] jako šipka z počátku')
ax.legend()
plt.show()
```
### Zápis vektorů
Vektory zapisujeme jako sloupec nebo řádek čísel:
$$\mathbf{v} = \begin{bmatrix} 3 \\ 2 \end{bmatrix} \quad \text{nebo} \quad \mathbf{v} = [3, 2]$$
::: {.callout-note title="Konvence"}
- Vektory značíme **tučně**: $\mathbf{v}$, $\mathbf{w}$, $\mathbf{x}$
- Nebo s šipkou: $\vec{v}$
- Jednotlivá čísla ve vektoru jsou **složky** (komponenty)
- Počet složek je **dimenze** vektoru
:::
```{python}
import numpy as np
# 2D vektor
v2 = np.array([3, 2])
print(f"2D vektor: {v2}")
print(f"Dimenze: {len(v2)}")
# 3D vektor
v3 = np.array([1, 2, 3])
print(f"\n3D vektor: {v3}")
print(f"Dimenze: {len(v3)}")
# Vektor s více dimenzemi (jako word embedding)
v100 = np.random.randn(100)
print(f"\n100D vektor (prvních 5 složek): {v100[:5].round(3)}...")
print(f"Dimenze: {len(v100)}")
```
## Skalár vs. vektor
| Skalár | Vektor |
|--------|--------|
| Jedno číslo | Více čísel |
| Např. teplota: 25°C | Např. pozice: [3, 2] |
| Pouze velikost | Velikost + směr |
| `x = 5` | `v = [3, 2]` |
```{python}
# Skalár
import numpy as np
teplota = 25.0
print(f"Skalár (teplota): {teplota}")
# Vektor
pozice = np.array([3.0, 2.0])
print(f"Vektor (pozice): {pozice}")
```
## Vektory v NumPy
NumPy je ideální nástroj pro práci s vektory.
### Vytváření vektorů
```{python}
# Ze seznamu
import numpy as np
v1 = np.array([1, 2, 3])
print("Ze seznamu:", v1)
# Nulový vektor
v_nuly = np.zeros(5)
print("Nulový vektor:", v_nuly)
# Vektor jedniček
v_jednicky = np.ones(4)
print("Vektor jedniček:", v_jednicky)
# Rovnoměrně rozložené hodnoty
v_linspace = np.linspace(0, 1, 5)
print("Linspace:", v_linspace)
# Náhodný vektor
np.random.seed(42)
v_nahodny = np.random.randn(4)
print("Náhodný:", v_nahodny.round(3))
```
### Přístup k složkám
```{python}
import numpy as np
v = np.array([10, 20, 30, 40, 50])
print(f"Celý vektor: {v}")
print(f"První složka (index 0): {v[0]}")
print(f"Třetí složka (index 2): {v[2]}")
print(f"Poslední složka: {v[-1]}")
print(f"Prvních 3 složky: {v[:3]}")
print(f"Od indexu 2 do konce: {v[2:]}")
```
## Délka (norma) vektoru
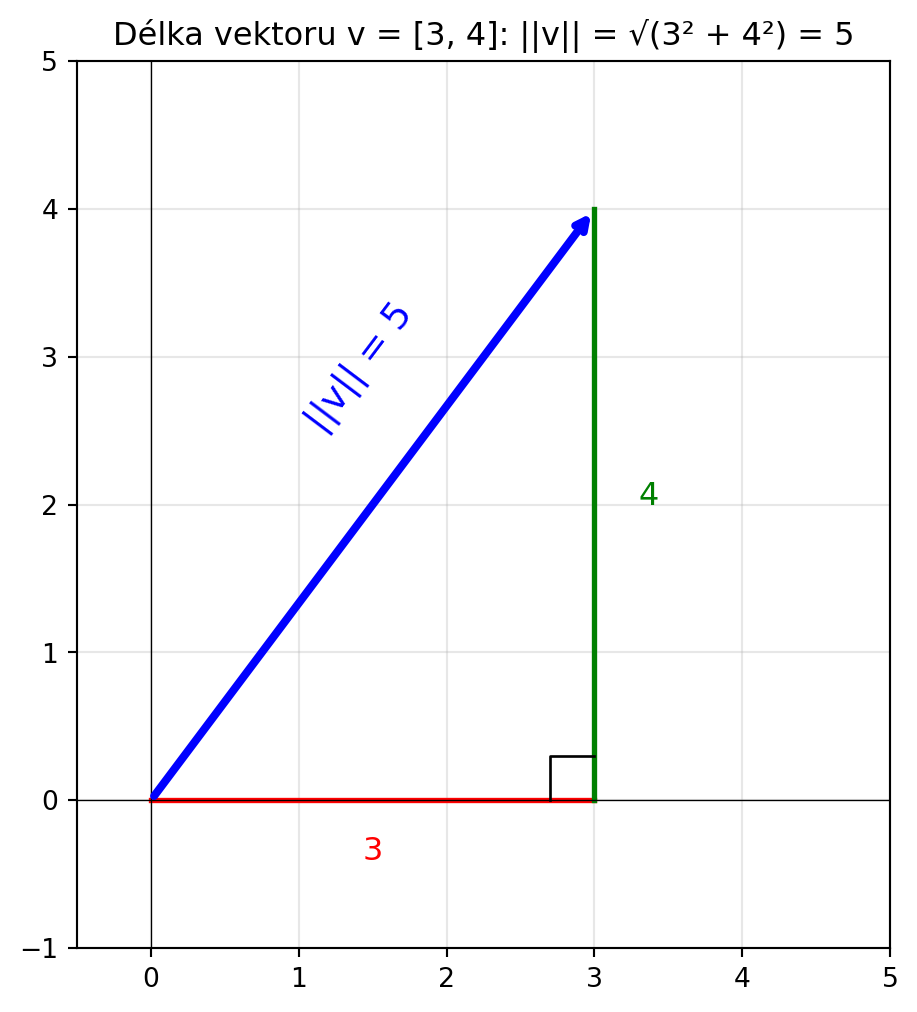
**Délka** neboli **norma** vektoru je jeho "velikost". Pro vektor $\mathbf{v} = [v_1, v_2, ..., v_n]$:
$$\|\mathbf{v}\| = \sqrt{v_1^2 + v_2^2 + ... + v_n^2}$$
Toto je **Euklidovská norma** (nebo L2 norma).
```{python}
#| fig-cap: "Délka vektoru"
#| code-fold: true
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 6))
v = np.array([3, 4])
# Vektor
ax.annotate('', xy=(3, 4), xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='blue', lw=3))
# Složky
ax.plot([0, 3], [0, 0], 'r-', linewidth=2)
ax.plot([3, 3], [0, 4], 'g-', linewidth=2)
# Popisky
ax.text(1.5, -0.4, '3', fontsize=12, color='red', ha='center')
ax.text(3.3, 2, '4', fontsize=12, color='green')
ax.text(1, 2.5, '||v|| = 5', fontsize=14, color='blue', rotation=53)
# Pravoúhlý trojúhelník
ax.plot([2.7, 2.7, 3], [0, 0.3, 0.3], 'k-', linewidth=1)
ax.set_xlim(-0.5, 5)
ax.set_ylim(-1, 5)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='k', linewidth=0.5)
ax.axvline(x=0, color='k', linewidth=0.5)
ax.set_title('Délka vektoru v = [3, 4]: ||v|| = √(3² + 4²) = 5')
plt.show()
```
```{python}
# Výpočet normy
import numpy as np
v = np.array([3, 4])
# Ručně
norma_rucne = np.sqrt(v[0]**2 + v[1]**2)
print(f"Norma (ručně): √({v[0]}² + {v[1]}²) = √{v[0]**2 + v[1]**2} = {norma_rucne}")
# Pomocí np.linalg.norm
norma = np.linalg.norm(v)
print(f"Norma (NumPy): {norma}")
# Pro vyšší dimenze
v_5d = np.array([1, 2, 3, 4, 5])
print(f"\nNorma 5D vektoru [1,2,3,4,5]: {np.linalg.norm(v_5d):.3f}")
```
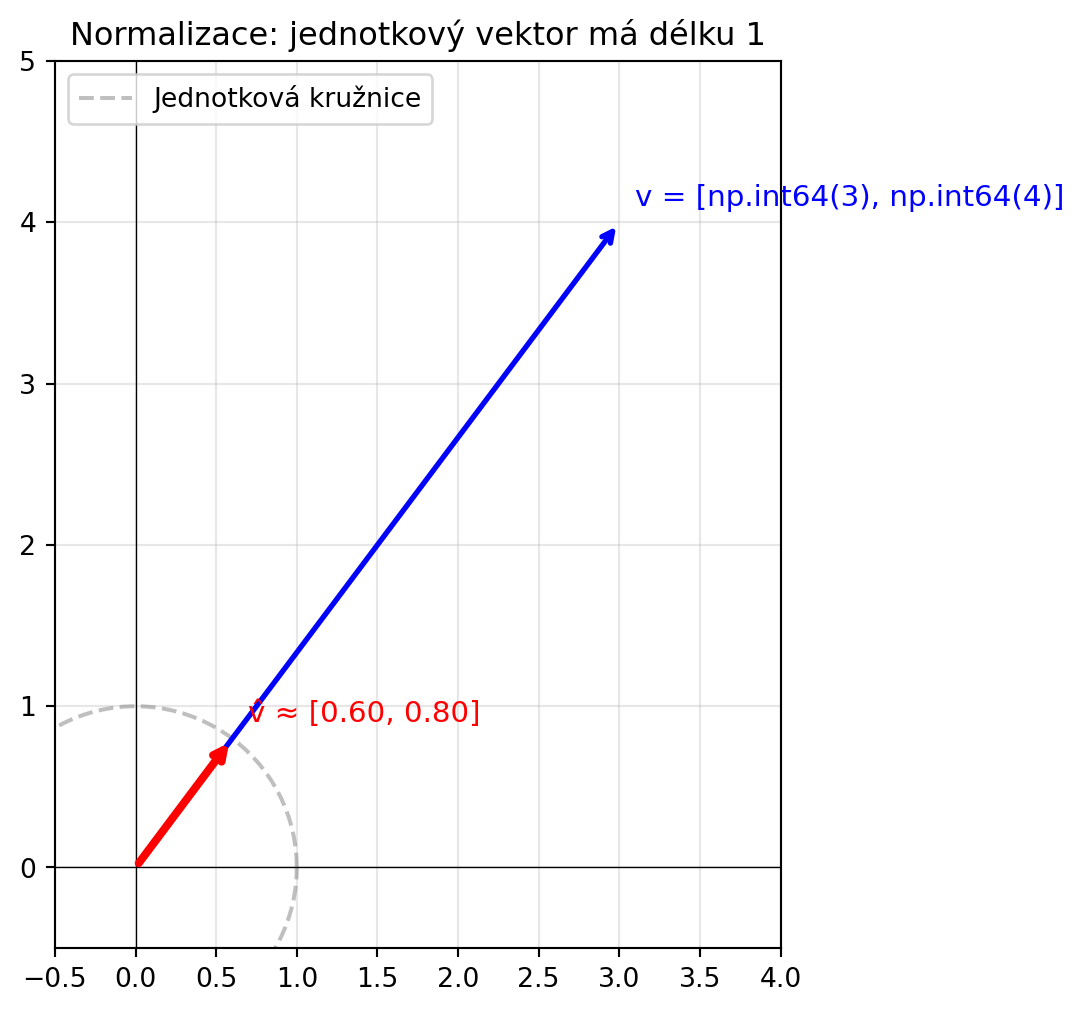
### Jednotkový vektor
**Jednotkový vektor** má délku 1. Vytvoříme ho **normalizací** -- dělením vektoru jeho normou:
$$\hat{\mathbf{v}} = \frac{\mathbf{v}}{\|\mathbf{v}\|}$$
```{python}
import numpy as np
v = np.array([3, 4])
# Normalizace
v_jednotkovy = v / np.linalg.norm(v)
print(f"Původní vektor: {v}")
print(f"Délka původního: {np.linalg.norm(v)}")
print(f"\nJednotkový vektor: {v_jednotkovy}")
print(f"Délka jednotkového: {np.linalg.norm(v_jednotkovy)}")
```
```{python}
#| fig-cap: "Původní vs. jednotkový vektor"
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 6))
v = np.array([3, 4])
v_norm = v / np.linalg.norm(v)
# Původní vektor
ax.annotate('', xy=v, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='blue', lw=2))
ax.text(v[0]+0.1, v[1]+0.1, f'v = {list(v)}', color='blue', fontsize=11)
# Jednotkový vektor
ax.annotate('', xy=v_norm, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color='red', lw=3))
ax.text(v_norm[0]+0.1, v_norm[1]+0.1, f'v̂ ≈ [{v_norm[0]:.2f}, {v_norm[1]:.2f}]',
color='red', fontsize=11)
# Jednotková kružnice
theta = np.linspace(0, 2*np.pi, 100)
ax.plot(np.cos(theta), np.sin(theta), 'gray', linestyle='--', alpha=0.5)
ax.set_xlim(-0.5, 4)
ax.set_ylim(-0.5, 5)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='k', linewidth=0.5)
ax.axvline(x=0, color='k', linewidth=0.5)
ax.set_title('Normalizace: jednotkový vektor má délku 1')
ax.legend(['Jednotková kružnice'], loc='upper left')
plt.show()
```
## Různé typy norem
Kromě Euklidovské normy (L2) existují i další:
| Norma | Vzorec | Význam |
|-------|--------|--------|
| L1 (Manhattan) | $\sum_i |v_i|$ | Součet absolutních hodnot |
| L2 (Euklidovská) | $\sqrt{\sum_i v_i^2}$ | "Vzdušná vzdálenost" |
| L∞ (Maximum) | $\max_i |v_i|$ | Největší složka |
```{python}
import numpy as np
v = np.array([3, -4, 2])
l1 = np.linalg.norm(v, ord=1)
l2 = np.linalg.norm(v, ord=2) # Výchozí
l_inf = np.linalg.norm(v, ord=np.inf)
print(f"Vektor: {v}")
print(f"L1 norma: |3| + |-4| + |2| = {l1}")
print(f"L2 norma: √(9 + 16 + 4) = {l2:.3f}")
print(f"L∞ norma: max(|3|, |-4|, |2|) = {l_inf}")
```
::: {.callout-tip title="Normy ve strojovém učení"}
- **L1 regularizace** podporuje řídké váhy (mnoho nul)
- **L2 regularizace** omezuje velikost vah (weight decay)
:::
---
## Geometrická interpretace
### Vektor jako posunutí
Vektor můžeme chápat jako instrukci "posuň se o tolik":
```{python}
#| fig-cap: "Vektor jako posunutí"
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 6))
# Několik vektorů z různých počátků
starts = [(0, 0), (2, 1), (1, 3)]
v = np.array([2, 1])
colors = ['blue', 'green', 'red']
for start, color in zip(starts, colors):
end = (start[0] + v[0], start[1] + v[1])
ax.annotate('', xy=end, xytext=start,
arrowprops=dict(arrowstyle='->', color=color, lw=2))
ax.plot(*start, 'o', color=color, markersize=8)
ax.text(4.5, 2, 'Všechny šipky reprezentují\nstejný vektor v = [2, 1]',
fontsize=11, bbox=dict(boxstyle='round', facecolor='wheat'))
ax.set_xlim(-1, 6)
ax.set_ylim(-1, 5)
ax.set_aspect('equal')
ax.grid(True, alpha=0.3)
ax.set_title('Stejný vektor z různých počátků')
plt.show()
```
### Polohový vektor
**Polohový vektor** má počátek v nule a určuje pozici bodu:
```{python}
#| fig-cap: "Polohové vektory bodů"
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 6))
body = {'A': [2, 3], 'B': [4, 1], 'C': [1, 4]}
barvy = ['blue', 'red', 'green']
for (nazev, bod), barva in zip(body.items(), barvy):
ax.annotate('', xy=bod, xytext=(0, 0),
arrowprops=dict(arrowstyle='->', color=barva, lw=2))
ax.plot(*bod, 'o', color=barva, markersize=10)
ax.text(bod[0]+0.15, bod[1]+0.15, f'{nazev}{bod}', fontsize=11, color=barva)
ax.axhline(y=0, color='k', linewidth=1)
ax.axvline(x=0, color='k', linewidth=1)
ax.grid(True, alpha=0.3)
ax.set_xlim(-0.5, 5)
ax.set_ylim(-0.5, 5)
ax.set_aspect('equal')
ax.set_title('Polohové vektory bodů A, B, C')
plt.show()
```
---
## Aplikace v praxi
### Word Embeddings
V jazykových modelech je každé slovo reprezentováno jako vektor (typicky 100-1000 dimenzí):
```{python}
# Simulace word embeddingů (zjednodušeno na 3D pro vizualizaci)
import numpy as np
np.random.seed(42)
# Podobná slova mají podobné vektory
slova = {
'král': np.array([0.5, 0.8, 0.2]),
'královna': np.array([0.6, 0.9, 0.3]),
'muž': np.array([0.4, 0.2, 0.1]),
'žena': np.array([0.5, 0.3, 0.2]),
'jablko': np.array([-0.5, 0.1, 0.8]),
'pomeranč': np.array([-0.4, 0.2, 0.7])
}
print("Word embeddings (3D zjednodušení):")
for slovo, vektor in slova.items():
print(f" {slovo:10}: {vektor}")
```
```{python}
#| fig-cap: "Word embeddings ve 3D prostoru"
#| code-fold: true
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
barvy = {'král': 'blue', 'královna': 'blue', 'muž': 'green',
'žena': 'green', 'jablko': 'red', 'pomeranč': 'red'}
for slovo, vektor in slova.items():
ax.scatter(*vektor, c=barvy[slovo], s=100)
ax.text(vektor[0], vektor[1], vektor[2], f' {slovo}', fontsize=10)
ax.set_xlabel('Dimenze 1')
ax.set_ylabel('Dimenze 2')
ax.set_zlabel('Dimenze 3')
ax.set_title('Word embeddings: podobná slova jsou blízko sebe')
plt.show()
```
### RGB barvy
Každá barva na obrazovce je vektor tří složek:
```{python}
#| fig-cap: "Barvy jako vektory"
# Barvy jako RGB vektory (0-255)
import numpy as np
import matplotlib.pyplot as plt
barvy = {
'Červená': np.array([255, 0, 0]),
'Zelená': np.array([0, 255, 0]),
'Modrá': np.array([0, 0, 255]),
'Žlutá': np.array([255, 255, 0]),
'Tyrkysová': np.array([0, 255, 255]),
'Fialová': np.array([255, 0, 255]),
'Oranžová': np.array([255, 165, 0]),
}
fig, ax = plt.subplots(figsize=(10, 3))
for i, (nazev, rgb) in enumerate(barvy.items()):
ax.add_patch(plt.Rectangle((i, 0), 1, 1, color=rgb/255))
ax.text(i+0.5, -0.15, nazev, ha='center', fontsize=9)
ax.text(i+0.5, 0.5, f'[{rgb[0]},{rgb[1]},{rgb[2]}]',
ha='center', va='center', fontsize=8, color='white' if sum(rgb) < 400 else 'black')
ax.set_xlim(0, len(barvy))
ax.set_ylim(-0.3, 1)
ax.axis('off')
ax.set_title('Barvy jako RGB vektory')
plt.show()
```
### Pozice ve hře
```{python}
# Pozice postav ve 2D hře
import numpy as np
hrac = np.array([5.0, 3.0])
nepritel = np.array([8.0, 7.0])
poklad = np.array([2.0, 6.0])
print(f"Hráč: {hrac}")
print(f"Nepřítel: {nepritel}")
print(f"Poklad: {poklad}")
# Vzdálenost k pokladu
vzdalenost = np.linalg.norm(poklad - hrac)
print(f"\nVzdálenost hráče k pokladu: {vzdalenost:.2f}")
```
---
## Řešené příklady
### Příklad 1: Vytvoření a norma
Vytvořte vektor $\mathbf{v} = [1, 2, 2]$ a vypočítejte jeho délku.
```{python}
import numpy as np
v = np.array([1, 2, 2])
norma = np.linalg.norm(v)
print(f"Vektor: {v}")
print(f"Norma: √(1² + 2² + 2²) = √(1 + 4 + 4) = √9 = {norma}")
```
### Příklad 2: Normalizace
Normalizujte vektor $\mathbf{u} = [4, 0, 3]$.
```{python}
import numpy as np
u = np.array([4, 0, 3])
norma_u = np.linalg.norm(u)
u_jednotkovy = u / norma_u
print(f"Původní: {u}")
print(f"Norma: √(16 + 0 + 9) = √25 = {norma_u}")
print(f"Jednotkový: {u_jednotkovy}")
print(f"Ověření délky: {np.linalg.norm(u_jednotkovy)}")
```
### Příklad 3: Různé normy
Vypočítejte L1, L2 a L∞ normu vektoru $\mathbf{w} = [-3, 4, 0, 2]$.
```{python}
import numpy as np
w = np.array([-3, 4, 0, 2])
print(f"Vektor: {w}")
print(f"L1: |-3| + |4| + |0| + |2| = {np.linalg.norm(w, 1)}")
print(f"L2: √(9 + 16 + 0 + 4) = √29 ≈ {np.linalg.norm(w, 2):.3f}")
print(f"L∞: max(3, 4, 0, 2) = {np.linalg.norm(w, np.inf)}")
```
### Příklad 4: Vzdálenost bodů
Vypočítejte vzdálenost mezi body A[1, 2, 3] a B[4, 6, 3].
```{python}
import numpy as np
A = np.array([1, 2, 3])
B = np.array([4, 6, 3])
# Vektor z A do B
AB = B - A
print(f"Vektor AB: {AB}")
# Vzdálenost = délka vektoru AB
vzdalenost = np.linalg.norm(AB)
print(f"Vzdálenost: √(3² + 4² + 0²) = √25 = {vzdalenost}")
```
### Příklad 5: Nejbližší slovo
Máme word embeddings. Které slovo je nejblíže slovu "král"?
```{python}
# Použijeme data z dřívějška
import numpy as np
kral = slova['král']
print("Vzdálenosti od slova 'král':")
for nazev, vektor in slova.items():
if nazev != 'král':
vzdalenost = np.linalg.norm(vektor - kral)
print(f" {nazev:10}: {vzdalenost:.3f}")
```
---
## Cvičení
::: {.callout-warning title="Cvičení 1: Vytvoření vektoru"}
Vytvořte vektor obsahující čísla 10, 20, 30, 40, 50 a zjistěte jeho dimenzi.
**Výsledek:** dimenze = 5
<details>
<summary>Řešení</summary>
```python
import numpy as np
v = np.array([10, 20, 30, 40, 50])
print(f"Vektor: {v}")
print(f"Dimenze: {len(v)}")
```
</details>
:::
::: {.callout-warning title="Cvičení 2: Norma vektoru"}
Vypočítejte délku vektoru $\mathbf{v} = [5, 12]$.
**Výsledek:** 13
<details>
<summary>Řešení</summary>
```python
import numpy as np
v = np.array([5, 12])
print(f"Norma: √(25 + 144) = √169 = {np.linalg.norm(v)}")
```
</details>
:::
::: {.callout-warning title="Cvičení 3: Jednotkový vektor"}
Najděte jednotkový vektor ve směru $\mathbf{u} = [0, 3, 4]$.
**Výsledek:** [0, 0.6, 0.8]
<details>
<summary>Řešení</summary>
```python
import numpy as np
u = np.array([0, 3, 4])
norma = np.linalg.norm(u) # = 5
u_hat = u / norma
print(f"Jednotkový: {u_hat}")
```
</details>
:::
::: {.callout-warning title="Cvičení 4: Vzdálenost"}
Jaká je vzdálenost mezi body P[1, 1, 1] a Q[4, 5, 1]?
**Výsledek:** 5
<details>
<summary>Řešení</summary>
```python
import numpy as np
P = np.array([1, 1, 1])
Q = np.array([4, 5, 1])
vzdalenost = np.linalg.norm(Q - P)
print(f"Vzdálenost: {vzdalenost}") # √(9 + 16 + 0) = 5
```
</details>
:::
::: {.callout-warning title="Cvičení 5: L1 norma"}
Vypočítejte L1 normu vektoru $\mathbf{w} = [2, -3, 1, -4]$.
**Výsledek:** 10
<details>
<summary>Řešení</summary>
```python
import numpy as np
w = np.array([2, -3, 1, -4])
l1 = np.linalg.norm(w, ord=1)
print(f"L1: |2| + |-3| + |1| + |-4| = {l1}")
```
</details>
:::
::: {.callout-warning title="Cvičení 6: RGB mix"}
Smícháním jaké barvy (RGB vektor) vznikne bílá?
**Výsledek:** [255, 255, 255]
<details>
<summary>Řešení</summary>
Bílá vznikne smícháním maximální intenzity všech složek:
```python
import numpy as np
bila = np.array([255, 255, 255])
print(f"Bílá: {bila}")
```
</details>
:::
---
## Shrnutí
::: {.callout-note title="Co si zapamatovat"}
- **Vektor** je uspořádaná n-tice čísel (seznam, pole)
- Vektor má **směr** a **velikost** (normu)
- **Norma** (délka): $\|\mathbf{v}\| = \sqrt{\sum v_i^2}$
- **Jednotkový vektor** má délku 1: $\hat{\mathbf{v}} = \frac{\mathbf{v}}{\|\mathbf{v}\|}$
- V NumPy: `np.array()`, `np.linalg.norm()`
- Vektory se používají všude: pozice, barvy, word embeddings
:::
V další kapitole se naučíme **operace s vektory** -- sčítání, násobení, a především skalární součin, který je základem pro měření podobnosti.