import numpy as np
import matplotlib.pyplot as plt
# Vytvoření matice v NumPy
A = np.array([
[1, 2, 3],
[4, 5, 6]
])
print("Matice A:")
print(A)
print(f"\nRozměr: {A.shape}") # (řádky, sloupce)Matice A:
[[1 2 3]
[4 5 6]]
Rozměr: (2, 3)V této kapitole se naučíte:
Matice je obdélníková tabulka čísel uspořádaná do řádků a sloupců.
\[\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}\]
Tato matice má 2 řádky a 3 sloupce – říkáme, že má rozměr 2×3 (čteme “dvě krát tři”).
import numpy as np
import matplotlib.pyplot as plt
# Vytvoření matice v NumPy
A = np.array([
[1, 2, 3],
[4, 5, 6]
])
print("Matice A:")
print(A)
print(f"\nRozměr: {A.shape}") # (řádky, sloupce)Matice A:
[[1 2 3]
[4 5 6]]
Rozměr: (2, 3)Matice jsou všudypřítomné v počítačích a strojovém učení:
# Jednoduchý obrázek jako matice (8x8 pixelů)
import numpy as np
import matplotlib.pyplot as plt
obrazek = np.array([
[0, 0, 1, 1, 1, 1, 0, 0],
[0, 1, 0, 0, 0, 0, 1, 0],
[1, 0, 1, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 1, 0, 0, 1],
[0, 1, 0, 0, 0, 0, 1, 0],
[0, 0, 1, 1, 1, 1, 0, 0]
])
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
# Jako obrázek
axes[0].imshow(obrazek, cmap='gray_r')
axes[0].set_title('Obrázek (vizualizace)')
axes[0].axis('off')
# Jako matice
axes[1].imshow(obrazek, cmap='gray_r')
axes[1].set_title('Matice (hodnoty pixelů)')
for i in range(8):
for j in range(8):
axes[1].text(j, i, str(obrazek[i, j]), ha='center', va='center',
color='white' if obrazek[i, j] == 1 else 'black', fontsize=10)
axes[1].set_xticks(range(8))
axes[1].set_yticks(range(8))
plt.tight_layout()
plt.show()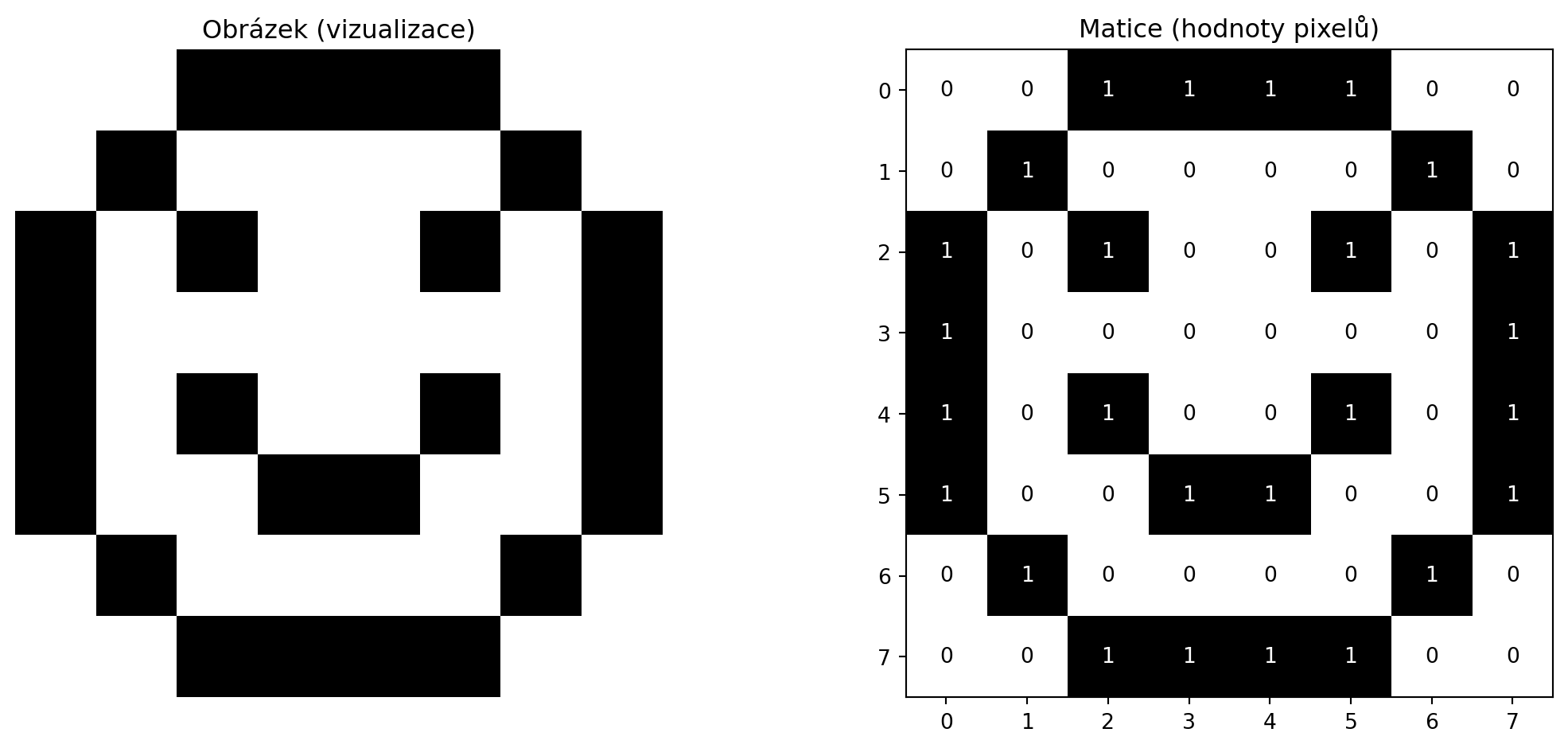
Matici o m řádcích a n sloupcích zapisujeme jako \(\mathbf{A} \in \mathbb{R}^{m \times n}\).
# Různé rozměry matic
import numpy as np
A = np.array([[1, 2], [3, 4], [5, 6]]) # 3×2
B = np.array([[1, 2, 3, 4]]) # 1×4 (řádkový vektor)
C = np.array([[1], [2], [3]]) # 3×1 (sloupcový vektor)
print(f"Matice A (3×2):\n{A}\n")
print(f"Řádkový vektor B (1×4):\n{B}\n")
print(f"Sloupcový vektor C (3×1):\n{C}")Matice A (3×2):
[[1 2]
[3 4]
[5 6]]
Řádkový vektor B (1×4):
[[1 2 3 4]]
Sloupcový vektor C (3×1):
[[1]
[2]
[3]]Prvek v řádku i a sloupci j značíme \(a_{ij}\) nebo \(A[i,j]\).
V Pythonu/NumPy indexujeme od 0, ne od 1!
import numpy as np
A = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
])
print("Matice A:")
print(A)
print(f"\nPrvek A[0,0] (1. řádek, 1. sloupec): {A[0, 0]}")
print(f"Prvek A[1,2] (2. řádek, 3. sloupec): {A[1, 2]}")
print(f"Prvek A[2,1] (3. řádek, 2. sloupec): {A[2, 1]}")Matice A:
[[1 2 3]
[4 5 6]
[7 8 9]]
Prvek A[0,0] (1. řádek, 1. sloupec): 1
Prvek A[1,2] (2. řádek, 3. sloupec): 6
Prvek A[2,1] (3. řádek, 2. sloupec): 8import numpy as np
A = np.array([
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
])
print("Matice A:")
print(A)
print(f"\n1. řádek: {A[0, :]}") # nebo A[0]
print(f"2. sloupec: {A[:, 1]}")
print(f"Podmatice (první 2 řádky, první 2 sloupce):")
print(A[:2, :2])Matice A:
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
1. řádek: [1 2 3 4]
2. sloupec: [ 2 6 10]
Podmatice (první 2 řádky, první 2 sloupce):
[[1 2]
[5 6]]Matice s stejným počtem řádků a sloupců (\(n \times n\)):
# Čtvercová matice 3×3
import numpy as np
M = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
])
print(f"Čtvercová matice {M.shape}:")
print(M)Čtvercová matice (3, 3):
[[1 2 3]
[4 5 6]
[7 8 9]]Jednotková matice \(\mathbf{I}\) má jedničky na diagonále a nuly jinde:
\[\mathbf{I}_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]
import numpy as np
I3 = np.eye(3) # Jednotková matice 3×3
print("Jednotková matice I₃:")
print(I3)
# Vlastnost: A × I = A
A = np.array([[1, 2], [3, 4]])
I2 = np.eye(2)
print(f"\nA × I = A:")
print(f"A =\n{A}")
print(f"A @ I =\n{A @ I2}")Jednotková matice I₃:
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
A × I = A:
A =
[[1 2]
[3 4]]
A @ I =
[[1. 2.]
[3. 4.]]Matice obsahující samé nuly:
import numpy as np
O = np.zeros((2, 3)) # 2×3 nulová matice
print("Nulová matice 2×3:")
print(O)Nulová matice 2×3:
[[0. 0. 0.]
[0. 0. 0.]]Matice s nenulovými prvky pouze na diagonále:
# Vytvoření z vektoru
import numpy as np
D = np.diag([1, 2, 3])
print("Diagonální matice:")
print(D)
# Získání diagonály z matice
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(f"\nDiagonála matice A: {np.diag(A)}")Diagonální matice:
[[1 0 0]
[0 2 0]
[0 0 3]]
Diagonála matice A: [1 5 9]Matice, která je stejná jako její transpozice (\(\mathbf{A} = \mathbf{A}^T\)):
import numpy as np
S = np.array([
[1, 2, 3],
[2, 4, 5],
[3, 5, 6]
])
print("Symetrická matice:")
print(S)
print(f"\nJe symetrická? {np.allclose(S, S.T)}")Symetrická matice:
[[1 2 3]
[2 4 5]
[3 5 6]]
Je symetrická? TrueTranspozice matice \(\mathbf{A}^T\) prohodí řádky a sloupce:
\[\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \quad \Rightarrow \quad \mathbf{A}^T = \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{bmatrix}\]
import numpy as np
A = np.array([
[1, 2, 3],
[4, 5, 6]
])
print("Původní matice A (2×3):")
print(A)
print(f"\nTransponovaná matice A^T (3×2):")
print(A.T)Původní matice A (2×3):
[[1 2 3]
[4 5 6]]
Transponovaná matice A^T (3×2):
[[1 4]
[2 5]
[3 6]]import numpy as np
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
A = np.array([[1, 2, 3], [4, 5, 6]])
for ax, (mat, title) in zip(axes, [(A, 'A (2×3)'), (A.T, 'Aᵀ (3×2)')]):
ax.imshow(np.zeros_like(mat), cmap='Blues', alpha=0.3)
for i in range(mat.shape[0]):
for j in range(mat.shape[1]):
ax.text(j, i, str(mat[i, j]), ha='center', va='center', fontsize=16)
ax.set_xticks(range(mat.shape[1]))
ax.set_yticks(range(mat.shape[0]))
ax.set_title(title, fontsize=14)
ax.set_xlim(-0.5, mat.shape[1]-0.5)
ax.set_ylim(mat.shape[0]-0.5, -0.5)
plt.tight_layout()
plt.show()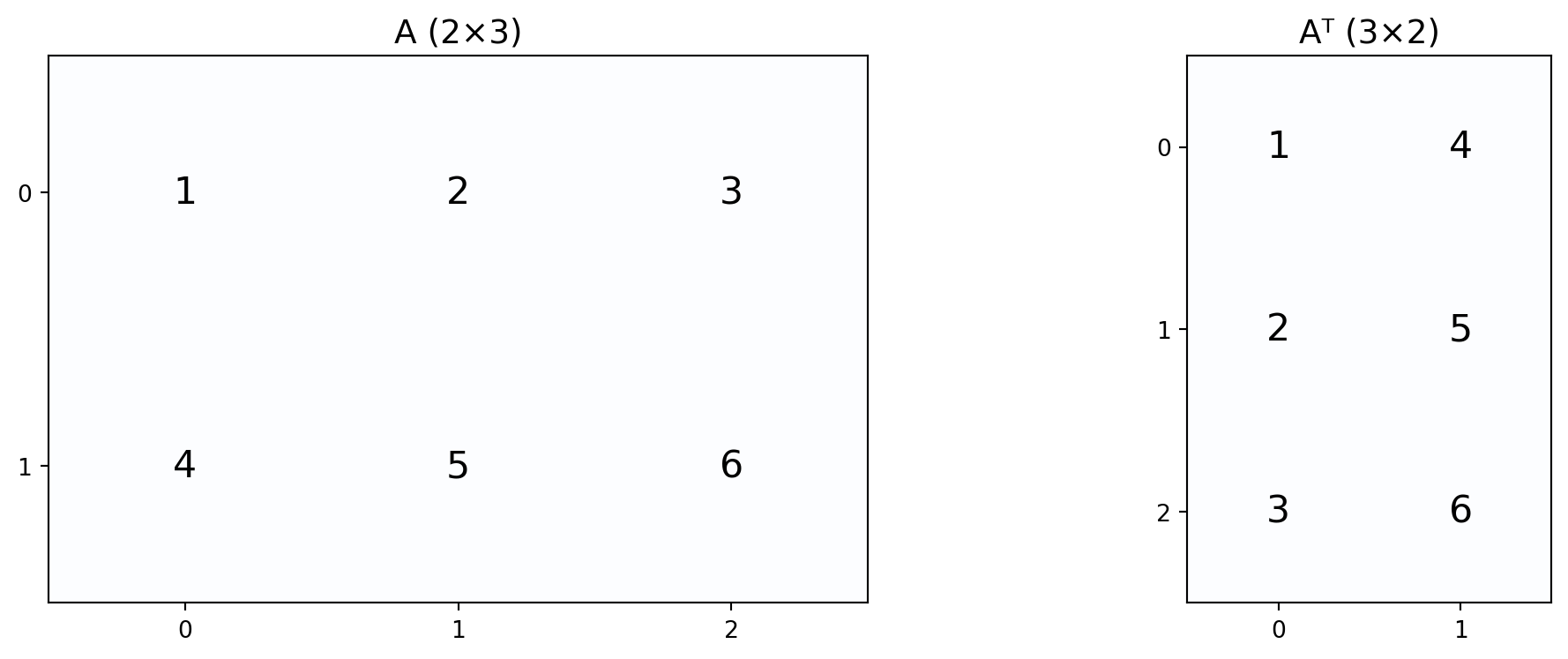
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
# (A^T)^T = A
print("(A^T)^T = A:")
print(f"A =\n{A}")
print(f"(A.T).T =\n{A.T.T}")
# (A + B)^T = A^T + B^T
print(f"\n(A + B)^T = A^T + B^T:")
print(f"(A + B).T =\n{(A + B).T}")
print(f"A.T + B.T =\n{A.T + B.T}")
# (AB)^T = B^T A^T (pozor na pořadí!)
print(f"\n(AB)^T = B^T A^T:")
print(f"(A @ B).T =\n{(A @ B).T}")
print(f"B.T @ A.T =\n{B.T @ A.T}")(A^T)^T = A:
A =
[[1 2]
[3 4]]
(A.T).T =
[[1 2]
[3 4]]
(A + B)^T = A^T + B^T:
(A + B).T =
[[ 6 10]
[ 8 12]]
A.T + B.T =
[[ 6 10]
[ 8 12]]
(AB)^T = B^T A^T:
(A @ B).T =
[[19 43]
[22 50]]
B.T @ A.T =
[[19 43]
[22 50]]# Ze seznamu
import numpy as np
A = np.array([[1, 2], [3, 4]])
print("Ze seznamu:")
print(A)
# Nulová matice
Z = np.zeros((2, 3))
print("\nNulová matice 2×3:")
print(Z)
# Matice jedniček
O = np.ones((3, 2))
print("\nMatice jedniček 3×2:")
print(O)
# Jednotková matice
I = np.eye(3)
print("\nJednotková matice 3×3:")
print(I)
# Náhodná matice
np.random.seed(42)
R = np.random.randn(2, 3) # Normální rozdělení
print("\nNáhodná matice 2×3:")
print(R.round(2))
# Matice s daným rozsahem
M = np.arange(1, 13).reshape(3, 4) # Čísla 1-12 do matice 3×4
print("\nMatice 3×4 s čísly 1-12:")
print(M)Ze seznamu:
[[1 2]
[3 4]]
Nulová matice 2×3:
[[0. 0. 0.]
[0. 0. 0.]]
Matice jedniček 3×2:
[[1. 1.]
[1. 1.]
[1. 1.]]
Jednotková matice 3×3:
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
Náhodná matice 2×3:
[[ 0.5 -0.14 0.65]
[ 1.52 -0.23 -0.23]]
Matice 3×4 s čísly 1-12:
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]Matice sčítáme po prvcích (musí mít stejné rozměry):
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
print("A + B (po prvcích):")
print(A + B)A + B (po prvcích):
[[ 6 8]
[10 12]]import numpy as np
A = np.array([[1, 2], [3, 4]])
print("3 * A:")
print(3 * A)3 * A:
[[ 3 6]
[ 9 12]]import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[2, 2], [2, 2]])
print("A * B (po prvcích, NE maticové násobení!):")
print(A * B)
print("\nA ** 2 (druhá mocnina po prvcích):")
print(A ** 2)A * B (po prvcích, NE maticové násobení!):
[[2 4]
[6 8]]
A ** 2 (druhá mocnina po prvcích):
[[ 1 4]
[ 9 16]]# Vytvoříme jednoduchý gradient
import numpy as np
import matplotlib.pyplot as plt
velikost = 100
obrazek = np.zeros((velikost, velikost))
# Vertikální gradient
for i in range(velikost):
obrazek[i, :] = i / velikost
fig, axes = plt.subplots(1, 4, figsize=(14, 3))
# Původní
axes[0].imshow(obrazek, cmap='gray')
axes[0].set_title('Původní')
axes[0].axis('off')
# Inverze
axes[1].imshow(1 - obrazek, cmap='gray')
axes[1].set_title('Inverze (1 - A)')
axes[1].axis('off')
# Zvýšení kontrastu
axes[2].imshow(obrazek ** 0.5, cmap='gray')
axes[2].set_title('Gamma korekce (A^0.5)')
axes[2].axis('off')
# Transpozice
axes[3].imshow(obrazek.T, cmap='gray')
axes[3].set_title('Transpozice (A^T)')
axes[3].axis('off')
plt.tight_layout()
plt.show()
Určete rozměr matice a najděte prvek \(a_{23}\):
\[\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{bmatrix}\]
import numpy as np
A = np.array([
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
])
print(f"Rozměr: {A.shape[0]}×{A.shape[1]}")
print(f"a₂₃ (2. řádek, 3. sloupec) = A[1,2] = {A[1, 2]}")Rozměr: 3×4
a₂₃ (2. řádek, 3. sloupec) = A[1,2] = 7Transponujte matici \(\mathbf{B} = \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{bmatrix}\)
import numpy as np
B = np.array([[1, 4], [2, 5], [3, 6]])
print("B (3×2):")
print(B)
print(f"\nB^T (2×3):")
print(B.T)B (3×2):
[[1 4]
[2 5]
[3 6]]
B^T (2×3):
[[1 2 3]
[4 5 6]]Sečtěte matice:
\[\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad \mathbf{B} = \begin{bmatrix} 5 & 1 \\ 0 & 2 \end{bmatrix}\]
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 1], [0, 2]])
print(f"A + B = ")
print(A + B)A + B =
[[6 3]
[3 6]]Stopa (trace) matice je součet prvků na diagonále.
import numpy as np
A = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
])
diagonala = np.diag(A)
stopa = np.trace(A)
print(f"Diagonála: {diagonala}")
print(f"Stopa (trace): {stopa}")
print(f"Ověření: 1 + 5 + 9 = {1 + 5 + 9}")Diagonála: [1 5 9]
Stopa (trace): 15
Ověření: 1 + 5 + 9 = 15Vytvořte matici 4×4, která má na diagonále čísla 1, 2, 3, 4.
import numpy as np
D = np.diag([1, 2, 3, 4])
print("Diagonální matice:")
print(D)Diagonální matice:
[[1 0 0 0]
[0 2 0 0]
[0 0 3 0]
[0 0 0 4]]Jaké rozměry má matice s 12 prvky uspořádanými do 3 řádků?
Výsledek: 3×4
V matice 5×5 s prvky 1 až 25 (po řádcích), jaká je hodnota prvku \(a_{34}\)?
Výsledek: 14
import numpy as np
A = np.arange(1, 26).reshape(5, 5)
print(A[2, 3]) # = 14Transponujte matici \(\begin{bmatrix} 1 & 2 & 3 \end{bmatrix}\). Jaký bude rozměr?
Výsledek: 3×1 (sloupcový vektor)
Vytvořte jednotkovou matici 5×5 pomocí NumPy.
import numpy as np
I5 = np.eye(5)
print(I5)Je matice \(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\) symetrická?
Výsledek: Ano
import numpy as np
A = np.array([[1, 2], [2, 1]])
print(f"Symetrická: {np.allclose(A, A.T)}")Jaká je stopa (trace) matice \(\begin{bmatrix} 3 & 1 & 4 \\ 1 & 5 & 9 \\ 2 & 6 & 5 \end{bmatrix}\)?
Výsledek: 13
A[i, j]np.array(), .shape, .T, np.eye(), np.zeros(), np.diag()V další kapitole se naučíme násobení matic – klíčovou operaci pro neuronové sítě a transformace dat.