# Co je funkce
::: {.callout-tip title="Co se naučíte"}
V této kapitole se naučíte:
- Co je matematická funkce
- Co je definiční obor a obor hodnot
- Jak vypadá graf funkce
- Rozlišovat rostoucí a klesající funkce
- Pracovat s funkcemi v Pythonu
:::
## Funkce jako stroj
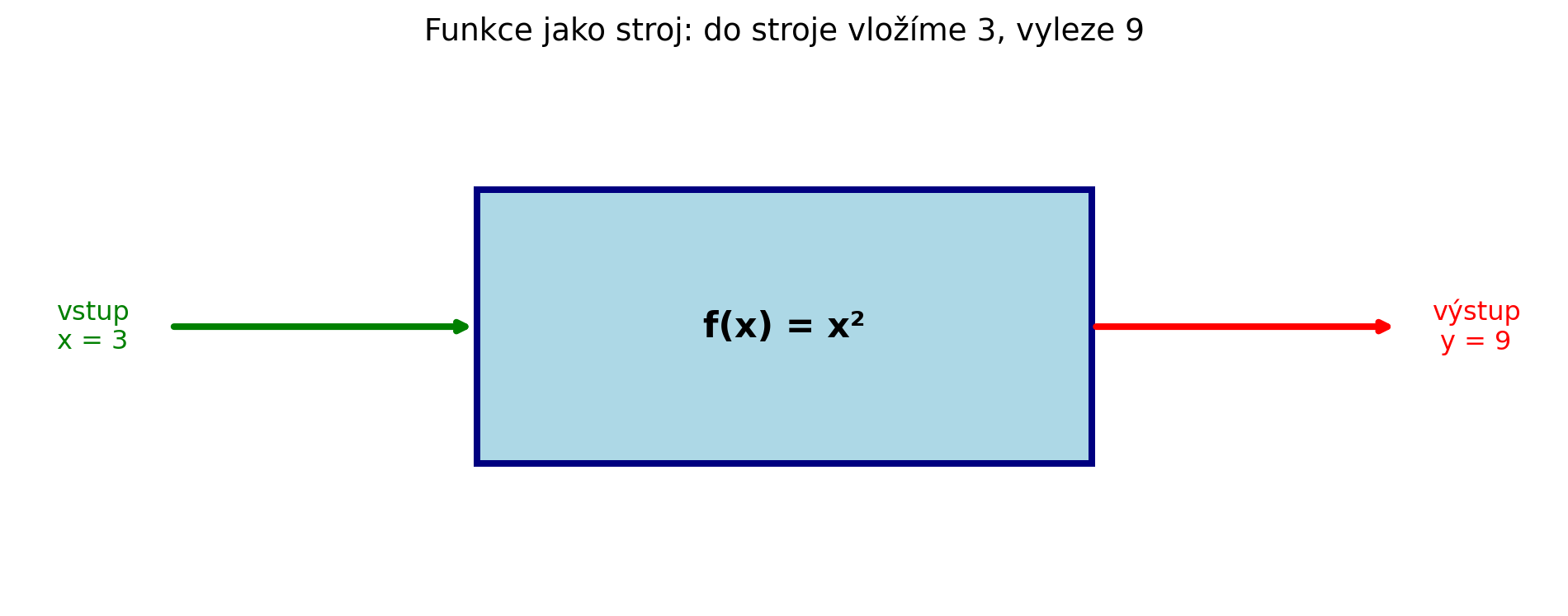
Představte si **funkci** jako stroj nebo továrnu:
1. Vložíte **vstup** (číslo, hodnotu)
2. Stroj provede nějakou operaci
3. Vyleze **výstup** (výsledek)
```{python}
#| fig-cap: "Funkce jako stroj"
#| code-fold: true
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
fig, ax = plt.subplots(figsize=(10, 4))
# Stroj (obdélník)
ax.add_patch(plt.Rectangle((3, 1), 4, 2, fill=True, facecolor='lightblue',
edgecolor='navy', linewidth=3))
ax.text(5, 2, 'f(x) = x²', fontsize=16, ha='center', va='center', fontweight='bold')
# Vstup
ax.annotate('', xy=(3, 2), xytext=(1, 2),
arrowprops=dict(arrowstyle='->', color='green', lw=3))
ax.text(0.5, 2, 'vstup\nx = 3', fontsize=12, ha='center', va='center', color='green')
# Výstup
ax.annotate('', xy=(9, 2), xytext=(7, 2),
arrowprops=dict(arrowstyle='->', color='red', lw=3))
ax.text(9.5, 2, 'výstup\ny = 9', fontsize=12, ha='center', va='center', color='red')
ax.set_xlim(0, 10)
ax.set_ylim(0, 4)
ax.axis('off')
ax.set_title('Funkce jako stroj: do stroje vložíme 3, vyleze 9', fontsize=14)
plt.tight_layout()
plt.show()
```
::: {.callout-note title="Definice"}
**Funkce** je předpis, který každému číslu z určité množiny přiřadí právě jedno číslo.
Zapisujeme: $f(x) = \text{předpis}$
Například: $f(x) = x^2$ znamená "vezmi číslo x a umocni ho na druhou"
:::
## Vstup a výstup
- **Vstup** (nezávisle proměnná) značíme obvykle **x**
- **Výstup** (závisle proměnná) značíme **y** nebo **f(x)**
Čteme: "f od x" nebo "funkční hodnota v bodě x"
```{python}
# Definujeme funkci v Pythonu
def f(x):
return x ** 2
# Vypočítáme několik hodnot
print(f"f(0) = {f(0)}")
print(f"f(1) = {f(1)}")
print(f"f(2) = {f(2)}")
print(f"f(3) = {f(3)}")
print(f"f(-2) = {f(-2)}") # Funguje i pro záporná čísla!
```
::: {.callout-tip title="Důležitý princip"}
Pro **stejný vstup** funkce vrátí vždy **stejný výstup**. Funkce je předvídatelná!
$f(3) = 9$ vždy, bez ohledu na to, kolikrát funkci zavoláme.
:::
## Definiční obor a obor hodnot
### Definiční obor
**Definiční obor** ($D_f$) je množina všech povolených vstupů.
```{python}
import numpy as np
# Funkce f(x) = √x -- nelze použít záporná čísla!
def g(x):
return np.sqrt(x)
print(f"√4 = {g(4)}")
print(f"√0 = {g(0)}")
# print(f"√(-1) = {g(-1)}") # Toto by způsobilo chybu nebo NaN!
```
::: {.callout-warning title="Typická omezení definičního oboru"}
- **Odmocnina**: pod odmocninou nesmí být záporné číslo
- **Dělení**: dělitel nesmí být nula
- **Logaritmus**: argument musí být kladný
:::
### Obor hodnot
**Obor hodnot** ($H_f$) je množina všech možných výstupů.
```{python}
# Funkce f(x) = x² může vrátit pouze nezáporná čísla
def f(x):
return x ** 2
# I pro záporný vstup je výstup kladný
print(f"f(-5) = {f(-5)}") # 25 (kladné!)
print(f"f(0) = {f(0)}") # 0
print(f"f(5) = {f(5)}") # 25
# Obor hodnot je [0, ∞) -- všechna nezáporná čísla
```
## Graf funkce
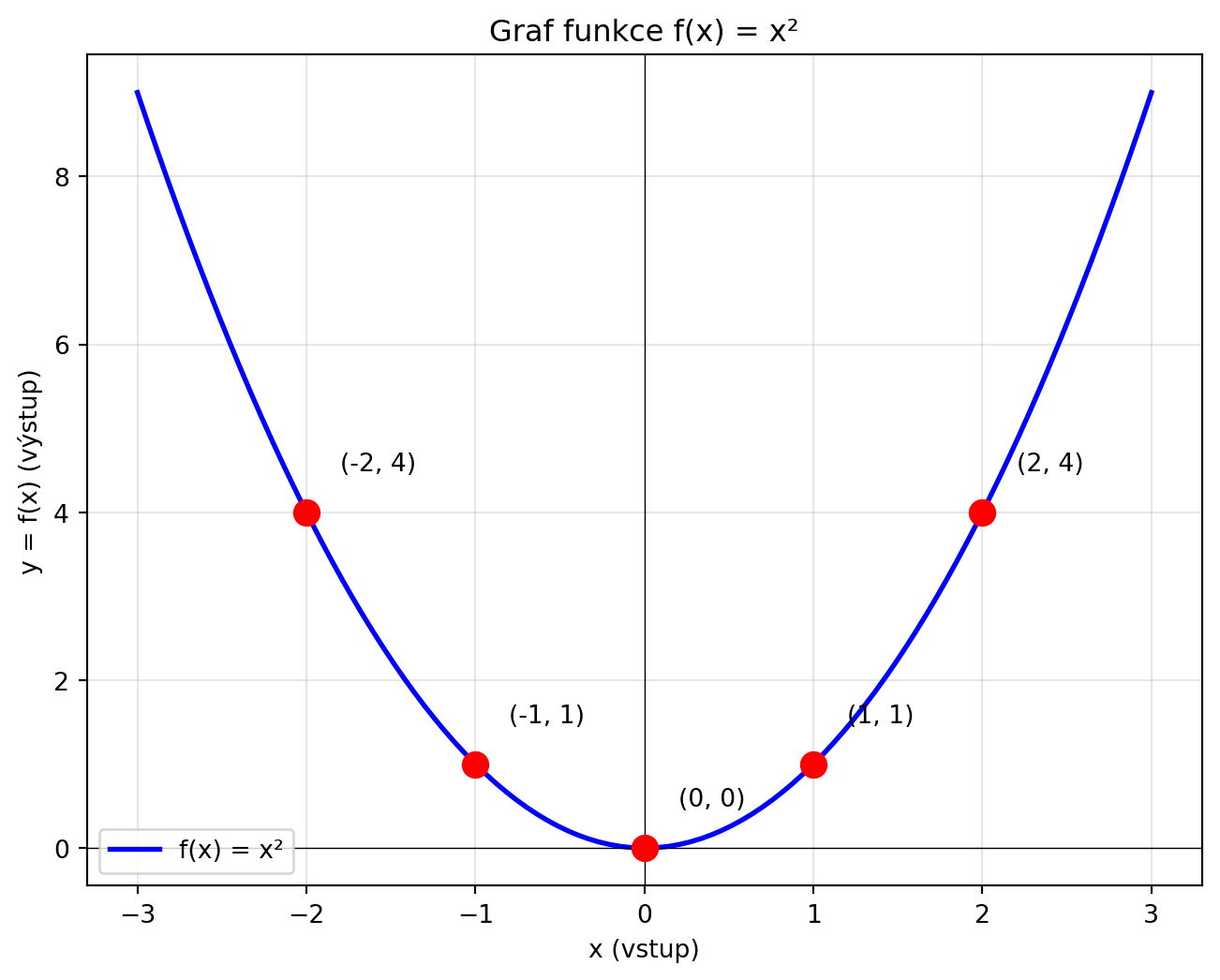
**Graf funkce** je vizuální zobrazení všech dvojic (vstup, výstup) v souřadnicovém systému.
```{python}
#| fig-cap: "Graf funkce f(x) = x²"
import numpy as np
import matplotlib.pyplot as plt
# Vytvoříme hodnoty x
x = np.linspace(-3, 3, 100)
# Vypočítáme hodnoty y
y = x ** 2
# Nakreslíme graf
plt.figure(figsize=(8, 6))
plt.plot(x, y, 'b-', linewidth=2, label='f(x) = x²')
# Označíme několik bodů
body_x = [-2, -1, 0, 1, 2]
body_y = [x**2 for x in body_x]
plt.scatter(body_x, body_y, color='red', s=100, zorder=5)
for bx, by in zip(body_x, body_y):
plt.annotate(f'({bx}, {by})', xy=(bx, by), xytext=(bx+0.2, by+0.5),
fontsize=10)
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x (vstup)')
plt.ylabel('y = f(x) (výstup)')
plt.title('Graf funkce f(x) = x²')
plt.legend()
plt.show()
```
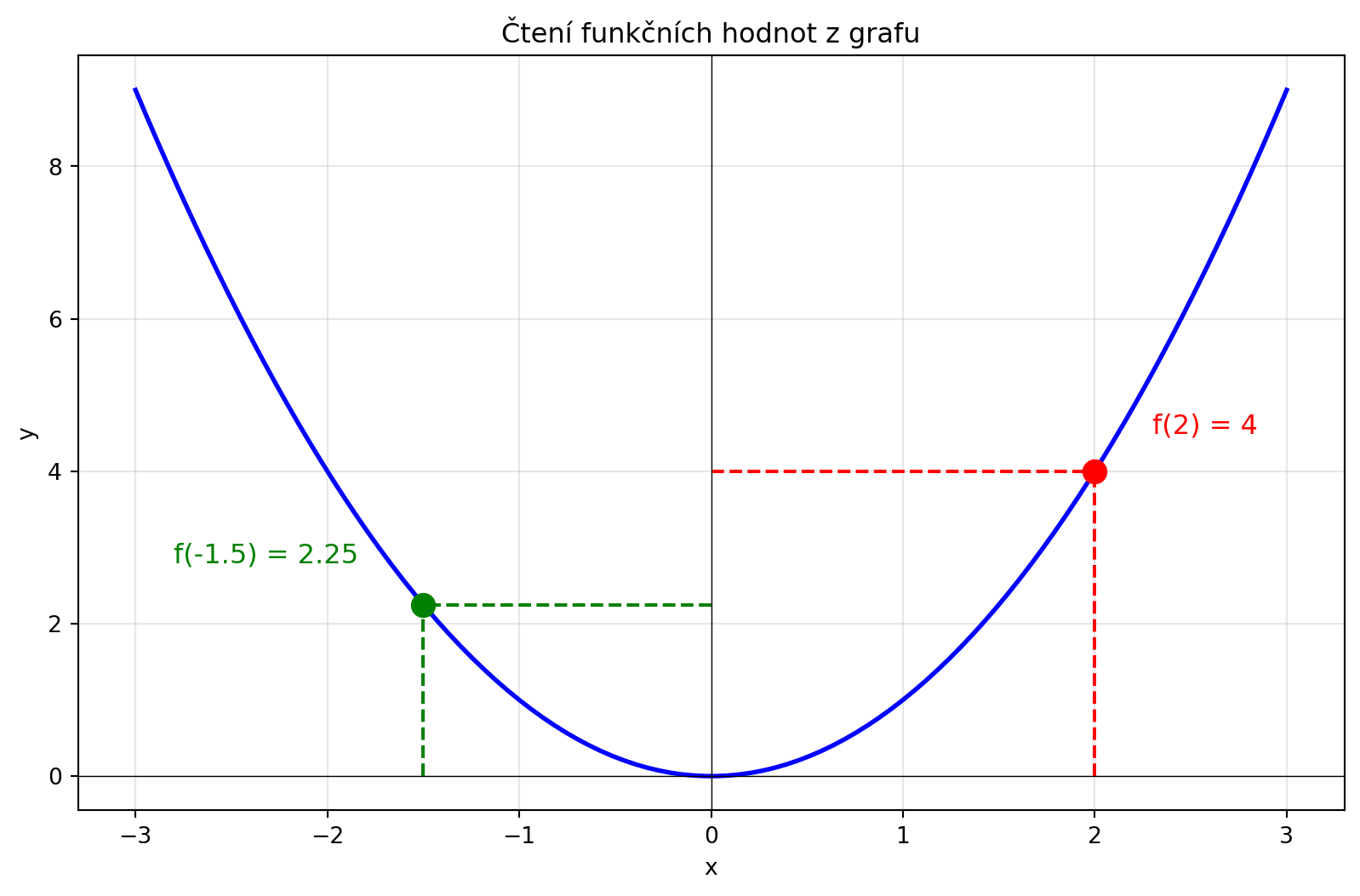
### Jak číst graf
Z grafu můžeme vyčíst:
1. **Funkční hodnotu** -- pro dané x najdeme odpovídající y
2. **Kde je funkce kladná/záporná** -- kde je graf nad/pod osou x
3. **Kde funkce roste/klesá** -- směr křivky
```{python}
#| fig-cap: "Čtení z grafu"
#| code-fold: true
import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10, 6))
x = np.linspace(-3, 3, 100)
y = x ** 2
ax.plot(x, y, 'b-', linewidth=2)
# Ukázka čtení: f(2) = 4
ax.plot([2, 2], [0, 4], 'r--', linewidth=1.5)
ax.plot([0, 2], [4, 4], 'r--', linewidth=1.5)
ax.plot(2, 4, 'ro', markersize=10)
ax.annotate('f(2) = 4', xy=(2, 4), xytext=(2.3, 4.5), fontsize=12, color='red')
# Ukázka: f(-1.5) = 2.25
ax.plot([-1.5, -1.5], [0, 2.25], 'g--', linewidth=1.5)
ax.plot([0, -1.5], [2.25, 2.25], 'g--', linewidth=1.5)
ax.plot(-1.5, 2.25, 'go', markersize=10)
ax.annotate('f(-1.5) = 2.25', xy=(-1.5, 2.25), xytext=(-2.8, 2.8), fontsize=12, color='green')
ax.axhline(y=0, color='k', linewidth=0.5)
ax.axvline(x=0, color='k', linewidth=0.5)
ax.grid(True, alpha=0.3)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Čtení funkčních hodnot z grafu')
plt.show()
```
## Rostoucí a klesající funkce
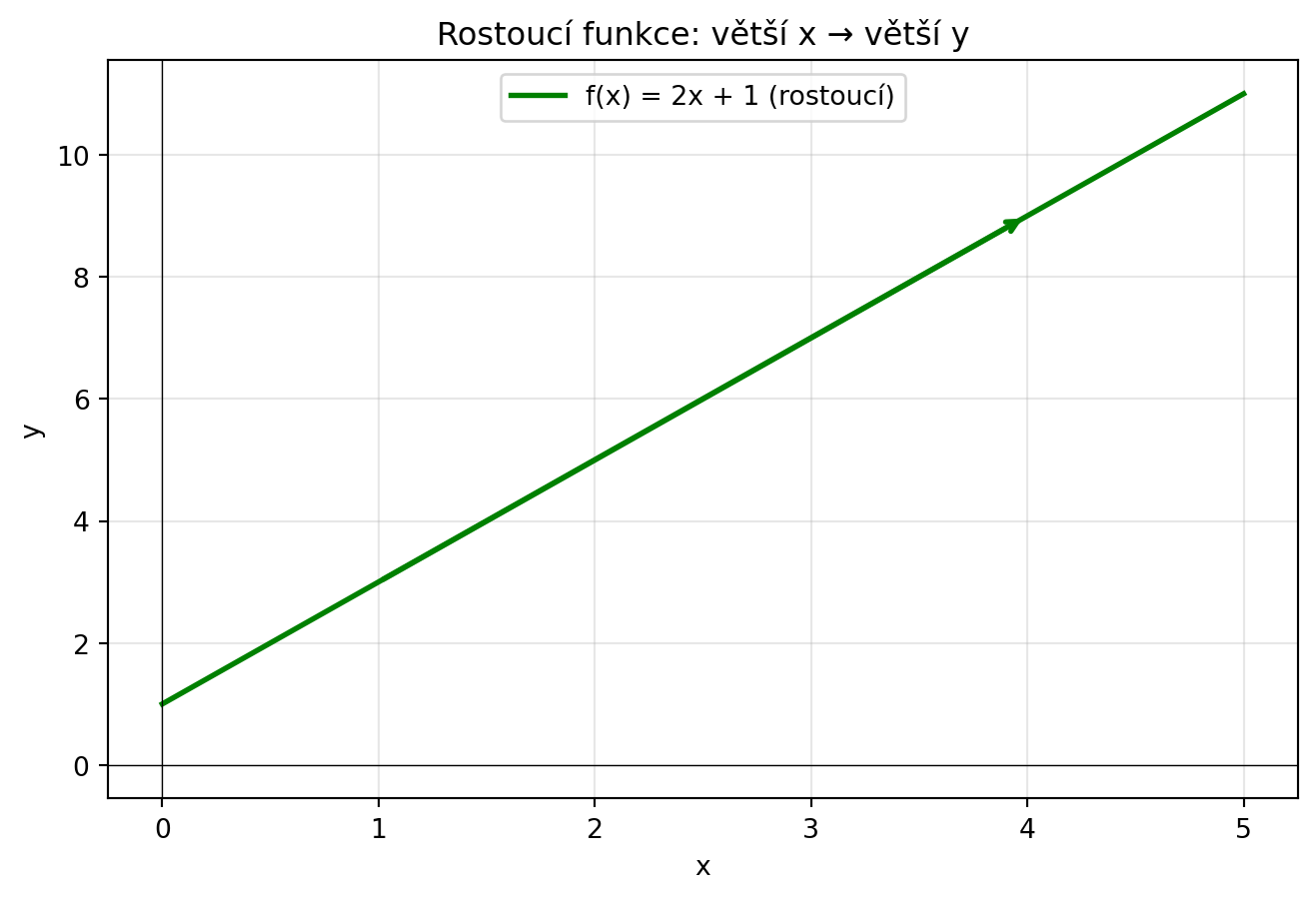
### Rostoucí funkce
Funkce je **rostoucí**, když větší vstup dává větší výstup.
$$\text{Pokud } x_1 < x_2, \text{ pak } f(x_1) < f(x_2)$$
```{python}
#| fig-cap: "Rostoucí funkce"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 5, 100)
y = 2 * x + 1
plt.figure(figsize=(8, 5))
plt.plot(x, y, 'g-', linewidth=2, label='f(x) = 2x + 1 (rostoucí)')
# Šipky ukazující růst
plt.annotate('', xy=(4, 9), xytext=(1, 3),
arrowprops=dict(arrowstyle='->', color='green', lw=2))
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Rostoucí funkce: větší x → větší y')
plt.legend()
plt.show()
```
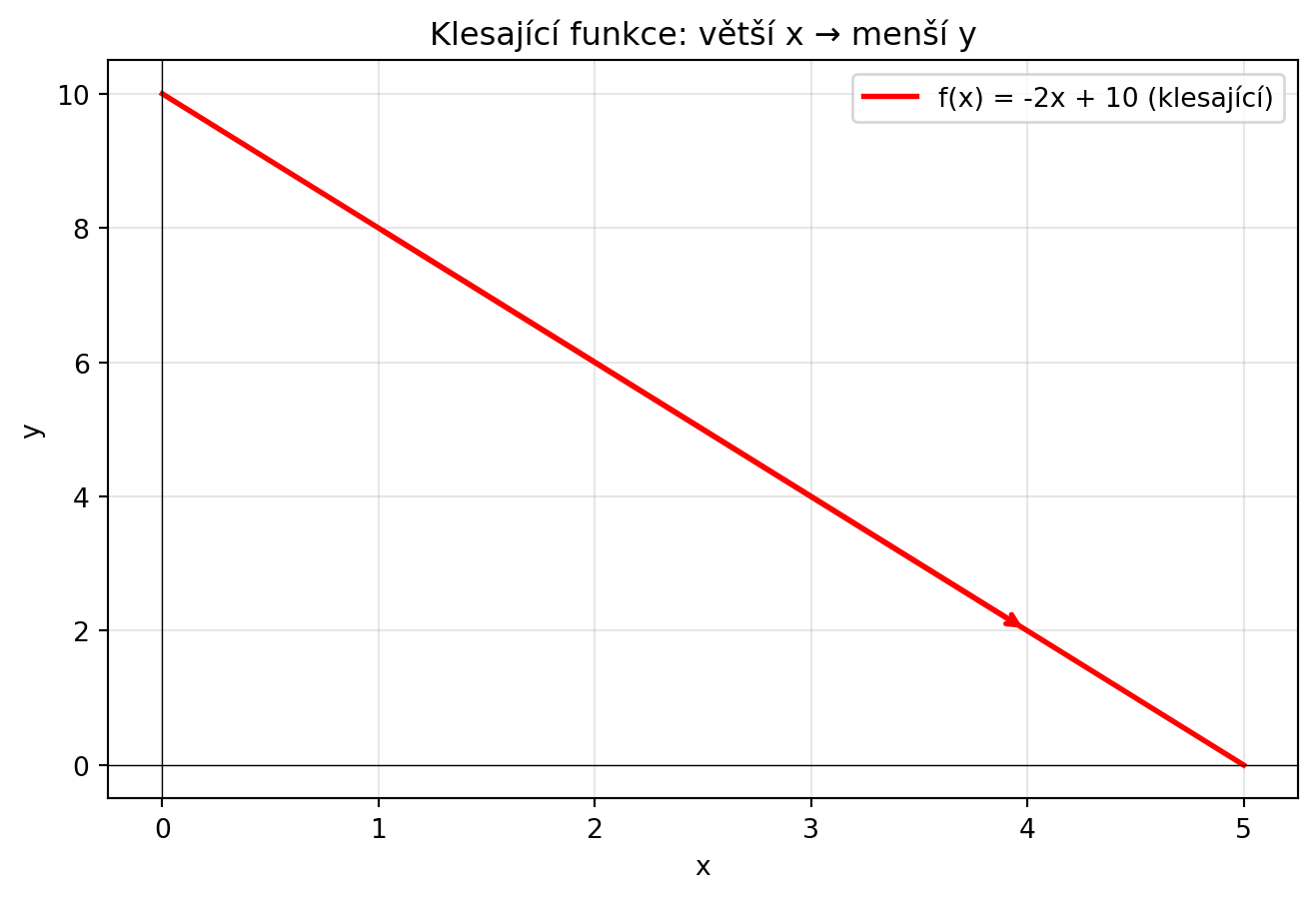
### Klesající funkce
Funkce je **klesající**, když větší vstup dává menší výstup.
$$\text{Pokud } x_1 < x_2, \text{ pak } f(x_1) > f(x_2)$$
```{python}
#| fig-cap: "Klesající funkce"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 5, 100)
y = -2 * x + 10
plt.figure(figsize=(8, 5))
plt.plot(x, y, 'r-', linewidth=2, label='f(x) = -2x + 10 (klesající)')
plt.annotate('', xy=(4, 2), xytext=(1, 8),
arrowprops=dict(arrowstyle='->', color='red', lw=2))
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Klesající funkce: větší x → menší y')
plt.legend()
plt.show()
```
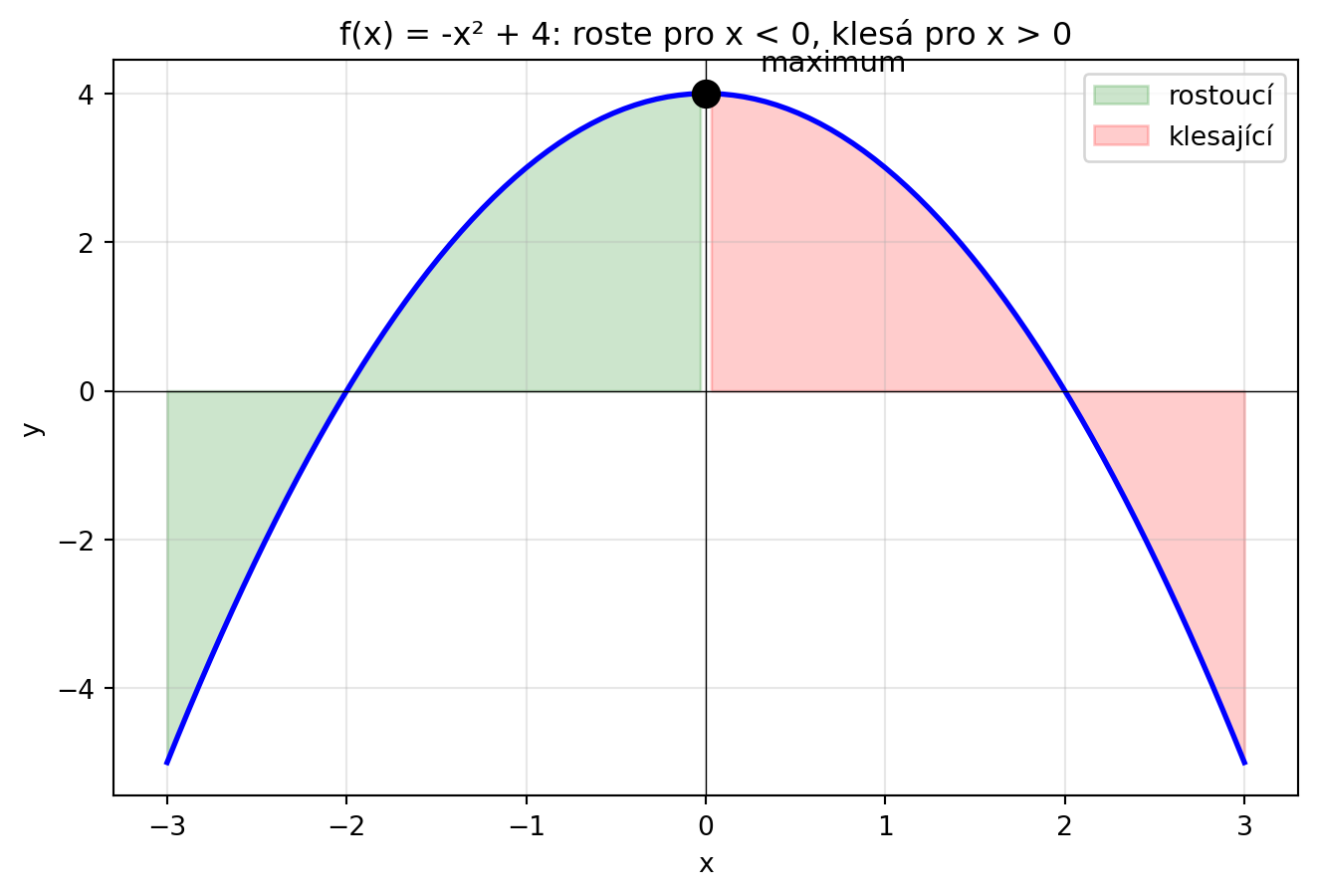
### Funkce může být obojí
Některé funkce rostou v jedné části a klesají v jiné:
```{python}
#| fig-cap: "Funkce, která roste i klesá"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3, 3, 100)
y = -x**2 + 4
plt.figure(figsize=(8, 5))
plt.plot(x, y, 'b-', linewidth=2)
# Označíme oblasti
plt.fill_between(x[x < 0], y[x < 0], alpha=0.2, color='green', label='rostoucí')
plt.fill_between(x[x > 0], y[x > 0], alpha=0.2, color='red', label='klesající')
plt.plot(0, 4, 'ko', markersize=10)
plt.annotate('maximum', xy=(0, 4), xytext=(0.3, 4.3), fontsize=11)
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('f(x) = -x² + 4: roste pro x < 0, klesá pro x > 0')
plt.legend()
plt.show()
```
## Funkce v programování
V Pythonu jsme už funkce používali! Matematické funkce a programátorské funkce mají mnoho společného:
```{python}
# Matematická funkce f(x) = 2x + 3
def linearni(x):
return 2 * x + 3
# Funkce s více vstupy (matematicky: funkce dvou proměnných)
def soucet(a, b):
return a + b
# Funkce pro výpočet obsahu kruhu
def obsah_kruhu(r):
return 3.14159 * r ** 2
print(f"f(5) = {linearni(5)}")
print(f"soucet(3, 4) = {soucet(3, 4)}")
print(f"obsah_kruhu(2) = {obsah_kruhu(2):.2f}")
```
### Tabulka hodnot
Užitečný způsob, jak prozkoumat funkci:
```{python}
def f(x):
return x**2 - 2*x
print("Tabulka hodnot pro f(x) = x² - 2x:")
print("-" * 20)
print(f"{'x':>5} | {'f(x)':>8}")
print("-" * 20)
for x in range(-3, 5):
print(f"{x:>5} | {f(x):>8}")
```
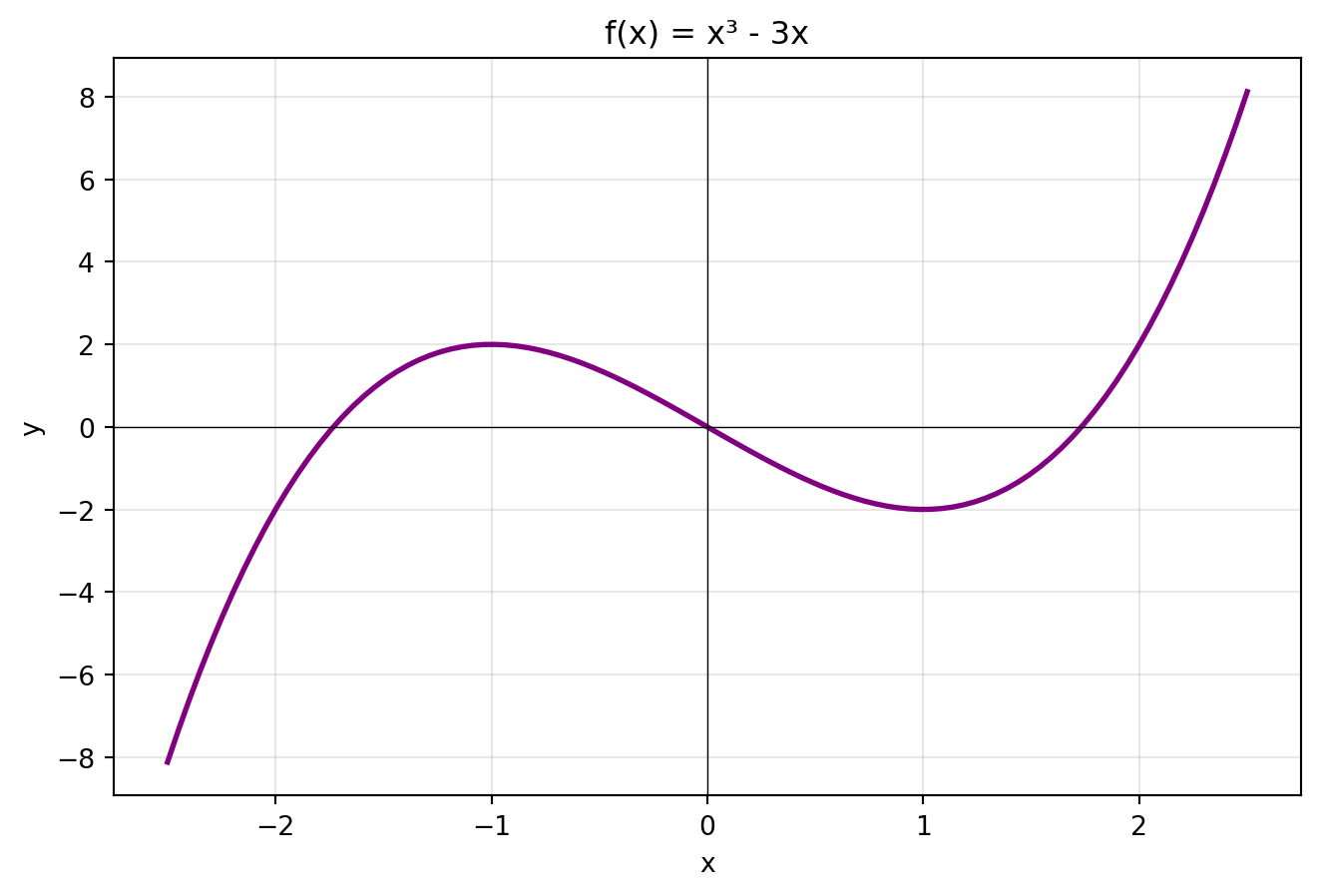
### Vykreslení libovolné funkce
```{python}
#| fig-cap: "Vlastní funkce"
import numpy as np
import matplotlib.pyplot as plt
def moje_funkce(x):
return x**3 - 3*x
x = np.linspace(-2.5, 2.5, 100)
y = moje_funkce(x)
plt.figure(figsize=(8, 5))
plt.plot(x, y, 'purple', linewidth=2)
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('f(x) = x³ - 3x')
plt.show()
```
---
## Aplikace v praxi
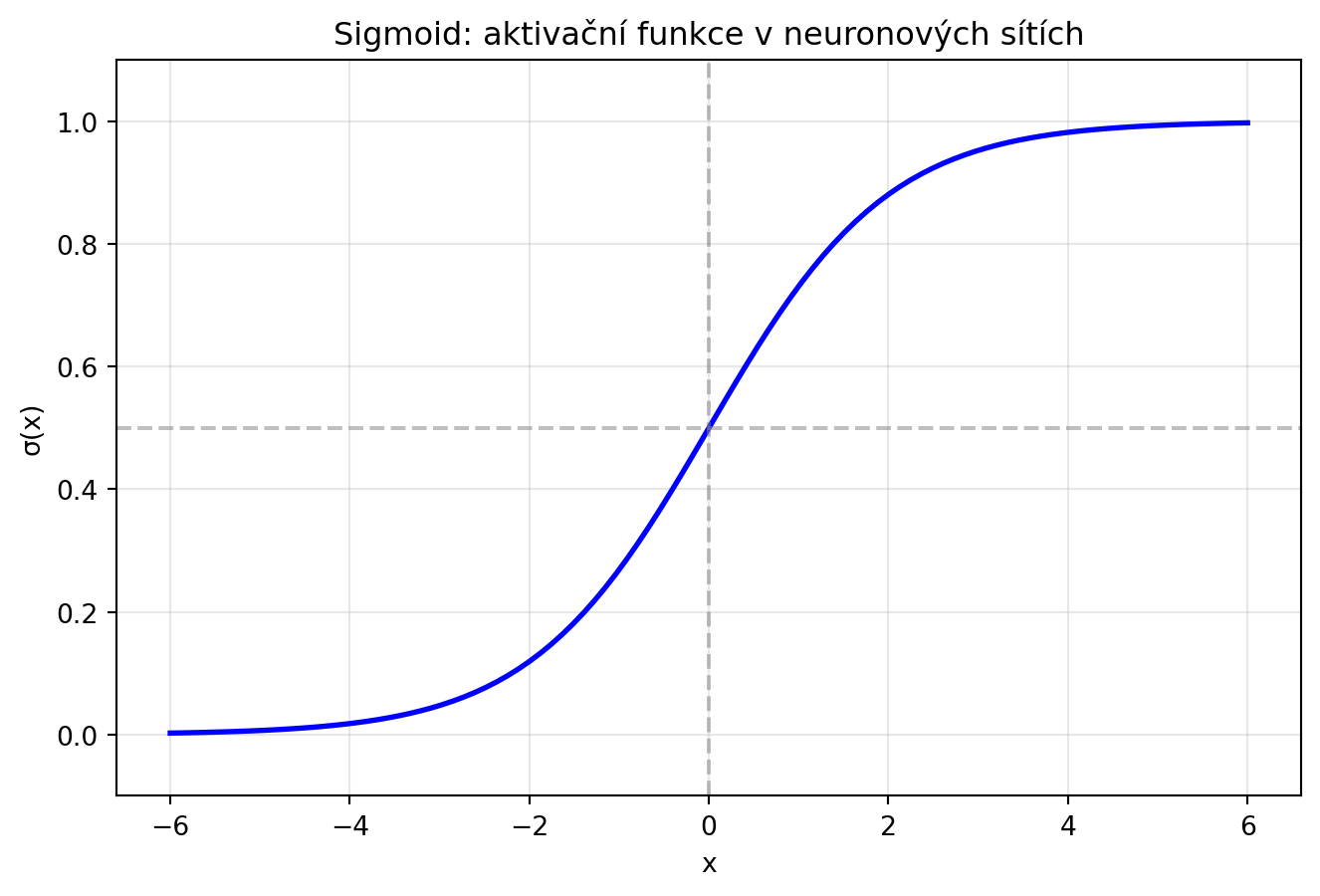
### Funkce v neuronových sítích
Neuronové sítě jsou složeny z funkcí! Každý **neuron** je jednoduchá funkce:
$$y = f(w_1 x_1 + w_2 x_2 + ... + b)$$
kde $f$ je tzv. **aktivační funkce**.
```{python}
#| fig-cap: "Aktivační funkce sigmoid"
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
"""Aktivační funkce používaná v neuronových sítích."""
return 1 / (1 + np.exp(-x))
x = np.linspace(-6, 6, 100)
y = sigmoid(x)
plt.figure(figsize=(8, 5))
plt.plot(x, y, 'b-', linewidth=2)
plt.axhline(y=0.5, color='gray', linestyle='--', alpha=0.5)
plt.axvline(x=0, color='gray', linestyle='--', alpha=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('σ(x)')
plt.title('Sigmoid: aktivační funkce v neuronových sítích')
plt.ylim(-0.1, 1.1)
plt.show()
```
### Převodní funkce
Mnoho praktických situací lze popsat funkcí:
```{python}
# Převod Celsius na Fahrenheit
def celsius_na_fahrenheit(c):
return c * 9/5 + 32
# Cena jízdy taxíkem
def cena_taxi(km):
nastupne = 40 # Kč
za_km = 28 # Kč/km
return nastupne + za_km * km
print("Teplota 20°C =", celsius_na_fahrenheit(20), "°F")
print("Taxi na 5 km stojí", cena_taxi(5), "Kč")
print("Taxi na 10 km stojí", cena_taxi(10), "Kč")
```
---
## Řešené příklady
### Příklad 1: Funkční hodnoty
Pro funkci $f(x) = 3x - 5$ vypočítejte $f(0)$, $f(2)$, $f(-1)$.
```{python}
def f(x):
return 3*x - 5
print(f"f(0) = 3·0 - 5 = {f(0)}")
print(f"f(2) = 3·2 - 5 = {f(2)}")
print(f"f(-1) = 3·(-1) - 5 = {f(-1)}")
```
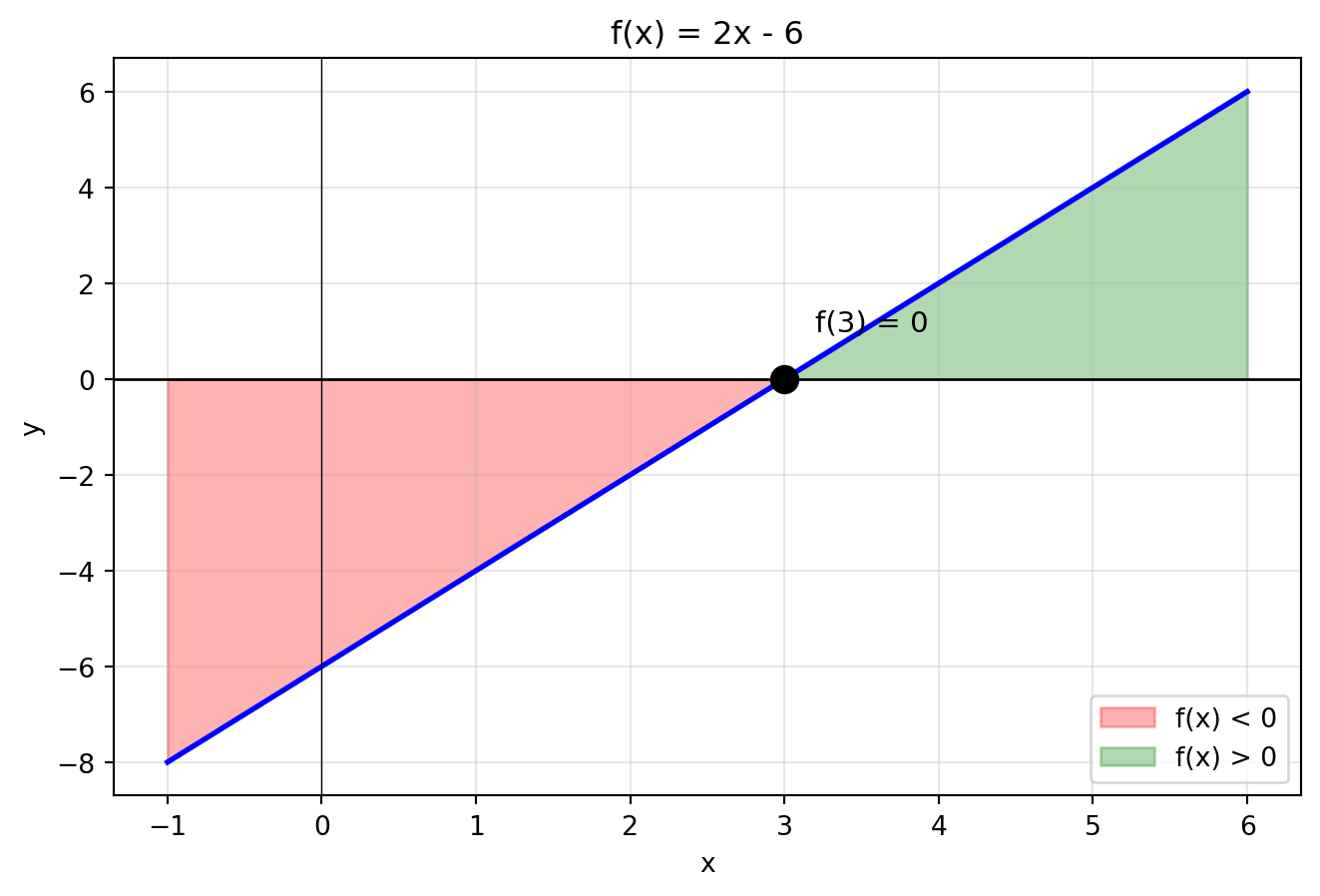
### Příklad 2: Kdy je funkce kladná?
Pro kterou hodnotu x je funkce $f(x) = 2x - 6$ rovna nule? Kdy je kladná?
**Řešení:**
$f(x) = 0$: $2x - 6 = 0 \Rightarrow x = 3$
$f(x) > 0$: $2x - 6 > 0 \Rightarrow x > 3$
```{python}
#| fig-cap: "Kde je funkce kladná/záporná"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1, 6, 100)
y = 2*x - 6
plt.figure(figsize=(8, 5))
plt.plot(x, y, 'b-', linewidth=2)
# Barevné oblasti
plt.fill_between(x[x < 3], y[x < 3], 0, alpha=0.3, color='red', label='f(x) < 0')
plt.fill_between(x[x > 3], y[x > 3], 0, alpha=0.3, color='green', label='f(x) > 0')
plt.plot(3, 0, 'ko', markersize=10)
plt.annotate('f(3) = 0', xy=(3, 0), xytext=(3.2, 1), fontsize=11)
plt.axhline(y=0, color='k', linewidth=1)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('f(x) = 2x - 6')
plt.legend()
plt.show()
```
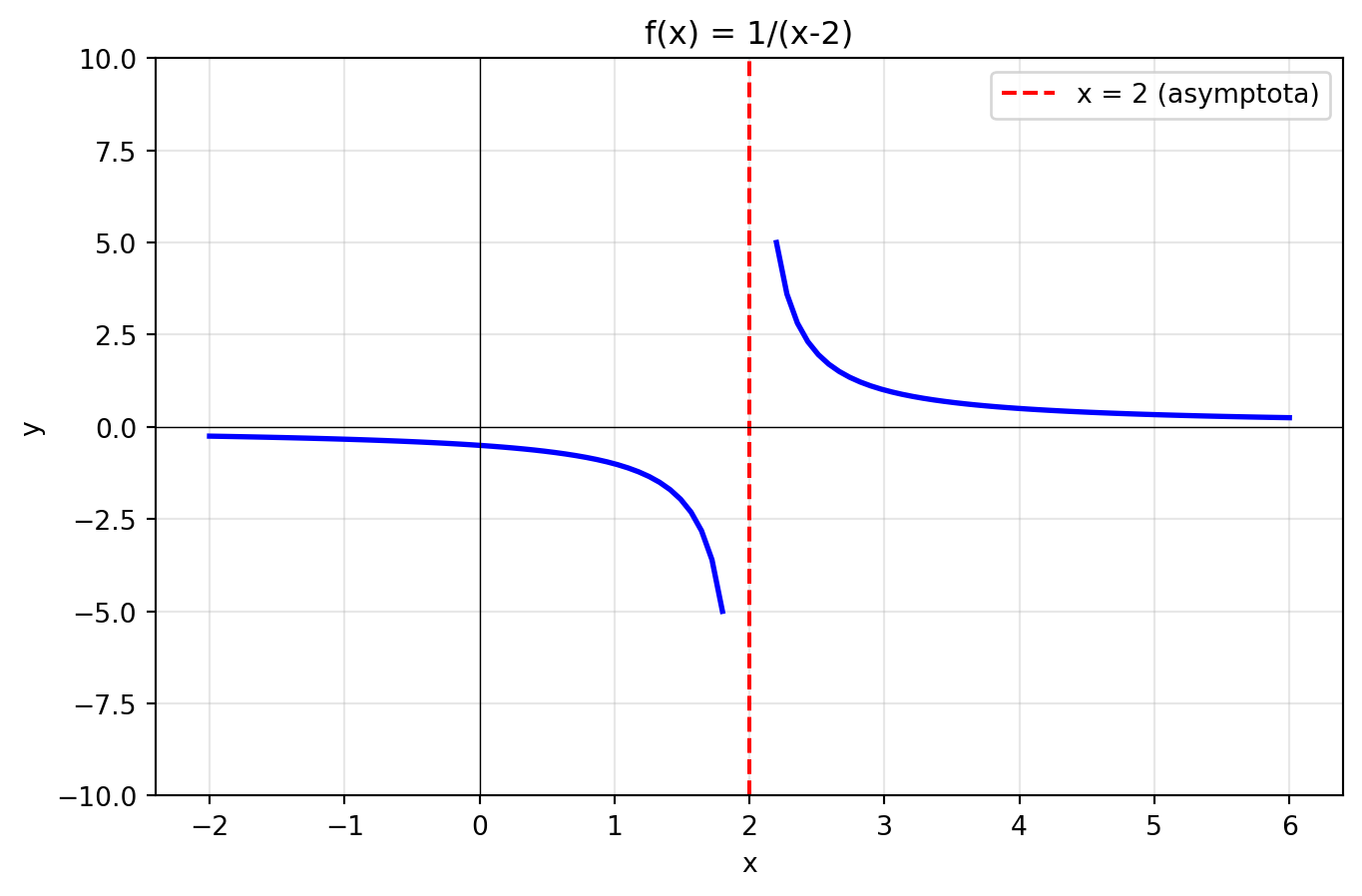
### Příklad 3: Definiční obor
Určete definiční obor funkce $f(x) = \frac{1}{x-2}$.
**Řešení:**
Jmenovatel nesmí být nula: $x - 2 \neq 0 \Rightarrow x \neq 2$
Definiční obor: $D_f = \mathbb{R} \setminus \{2\}$ (všechna reálná čísla kromě 2)
```{python}
#| fig-cap: "Funkce s omezeným definičním oborem"
# Musíme nakreslit dvě větve (před a za x=2)
import numpy as np
import matplotlib.pyplot as plt
x1 = np.linspace(-2, 1.8, 50)
x2 = np.linspace(2.2, 6, 50)
y1 = 1 / (x1 - 2)
y2 = 1 / (x2 - 2)
plt.figure(figsize=(8, 5))
plt.plot(x1, y1, 'b-', linewidth=2)
plt.plot(x2, y2, 'b-', linewidth=2)
# Svislá asymptota
plt.axvline(x=2, color='red', linestyle='--', label='x = 2 (asymptota)')
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('f(x) = 1/(x-2)')
plt.ylim(-10, 10)
plt.legend()
plt.show()
```
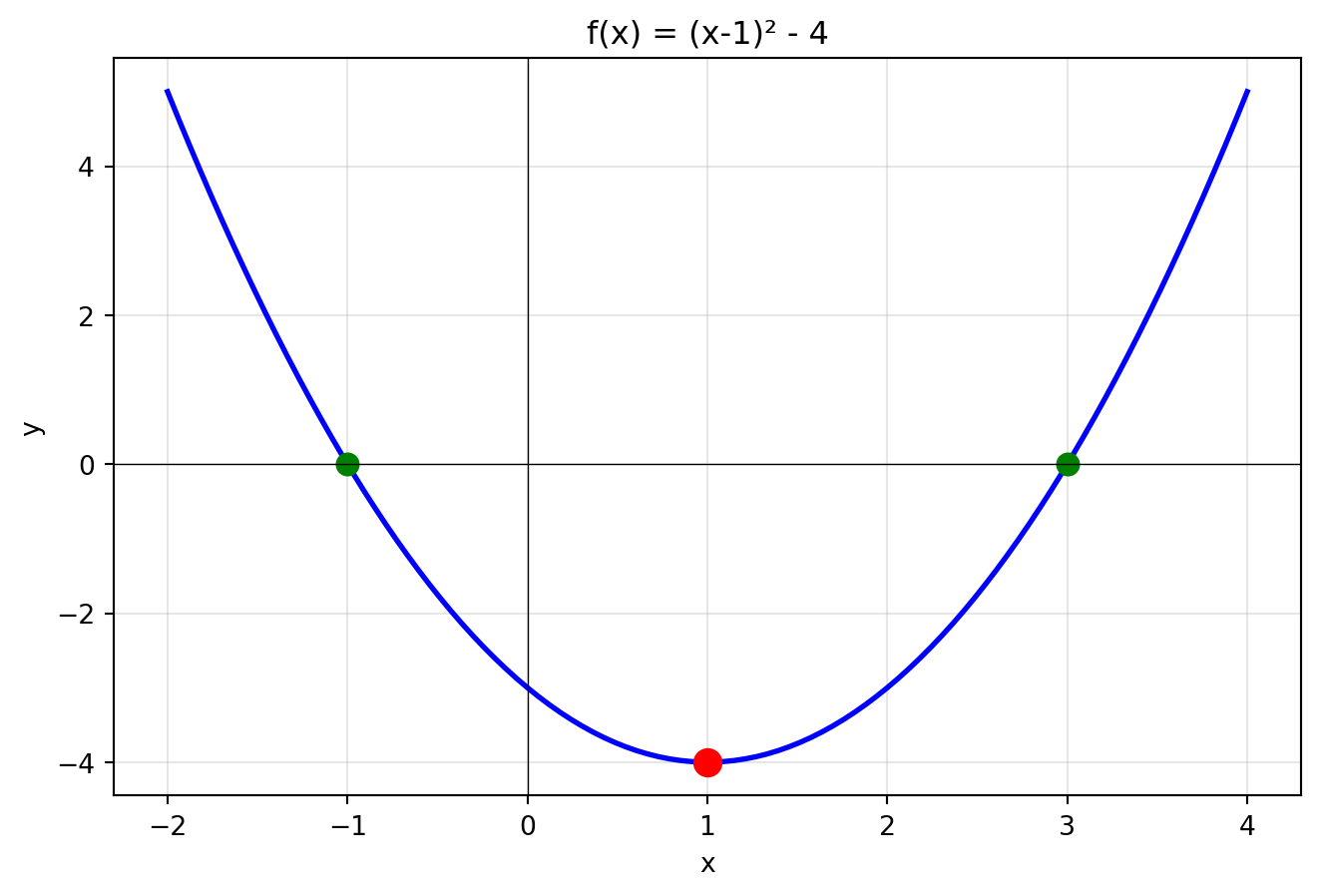
### Příklad 4: Z grafu určete vlastnosti
```{python}
#| fig-cap: "Analyzujte tuto funkci"
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 4, 100)
y = (x - 1)**2 - 4
plt.figure(figsize=(8, 5))
plt.plot(x, y, 'b-', linewidth=2)
plt.plot(1, -4, 'ro', markersize=10) # Minimum
plt.plot([-1, 3], [0, 0], 'go', markersize=8) # Průsečíky s osou x
plt.axhline(y=0, color='k', linewidth=0.5)
plt.axvline(x=0, color='k', linewidth=0.5)
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('y')
plt.title('f(x) = (x-1)² - 4')
plt.show()
```
**Z grafu vyčteme:**
- Minimum je v bodě [1, -4]
- Funkce protíná osu x v bodech x = -1 a x = 3
- Funkce klesá pro x < 1, roste pro x > 1
### Příklad 5: Složená funkce
Máme $f(x) = x^2$ a $g(x) = x + 1$. Vypočítejte $f(g(2))$ a $g(f(2))$.
```{python}
def f(x):
return x ** 2
def g(x):
return x + 1
# f(g(2)) = f(3) = 9
print(f"g(2) = {g(2)}")
print(f"f(g(2)) = f({g(2)}) = {f(g(2))}")
# g(f(2)) = g(4) = 5
print(f"\nf(2) = {f(2)}")
print(f"g(f(2)) = g({f(2)}) = {g(f(2))}")
print("\nPozor: f(g(x)) ≠ g(f(x))!")
```
---
## Cvičení
::: {.callout-warning title="Cvičení 1: Funkční hodnoty"}
Pro funkci $f(x) = x^2 + 2x - 3$ vypočítejte $f(-2)$, $f(0)$, $f(1)$, $f(3)$.
**Výsledky:** -3, -3, 0, 12
<details>
<summary>Řešení</summary>
```python
def f(x):
return x**2 + 2*x - 3
print(f"f(-2) = {f(-2)}") # (-2)² + 2·(-2) - 3 = 4 - 4 - 3 = -3
print(f"f(0) = {f(0)}") # 0 + 0 - 3 = -3
print(f"f(1) = {f(1)}") # 1 + 2 - 3 = 0
print(f"f(3) = {f(3)}") # 9 + 6 - 3 = 12
```
</details>
:::
::: {.callout-warning title="Cvičení 2: Graf funkce"}
Nakreslete graf funkce $f(x) = -x + 3$ pro $x \in [-2, 5]$.
<details>
<summary>Řešení</summary>
```python
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 5, 100)
y = -x + 3
plt.plot(x, y)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('y')
plt.title('f(x) = -x + 3')
plt.show()
```
</details>
:::
::: {.callout-warning title="Cvičení 3: Definiční obor"}
Určete definiční obor funkcí:
a) $f(x) = \sqrt{x - 4}$
b) $g(x) = \frac{1}{x^2 - 1}$
<details>
<summary>Řešení</summary>
a) $x - 4 \geq 0 \Rightarrow x \geq 4$, tedy $D_f = [4, \infty)$
b) $x^2 - 1 \neq 0 \Rightarrow x \neq \pm 1$, tedy $D_g = \mathbb{R} \setminus \{-1, 1\}$
</details>
:::
::: {.callout-warning title="Cvičení 4: Rostoucí nebo klesající?"}
Určete, zda jsou následující funkce rostoucí nebo klesající:
a) $f(x) = 5x + 2$
b) $g(x) = -3x + 7$
c) $h(x) = x^2$
<details>
<summary>Řešení</summary>
a) Rostoucí (koeficient u x je kladný)
b) Klesající (koeficient u x je záporný)
c) Klesající pro x < 0, rostoucí pro x > 0
</details>
:::
::: {.callout-warning title="Cvičení 5: Praktická úloha"}
Měsíční paušál za telefon je 199 Kč + 2 Kč za každou SMS. Napište funkci `cena(pocet_sms)` a vypočítejte cenu za 50 SMS.
**Výsledek:** 299 Kč
<details>
<summary>Řešení</summary>
```python
def cena(pocet_sms):
pausal = 199
cena_sms = 2
return pausal + cena_sms * pocet_sms
print(f"Cena za 50 SMS: {cena(50)} Kč")
```
</details>
:::
::: {.callout-warning title="Cvičení 6: Tabulka hodnot"}
Vytvořte tabulku hodnot pro funkci $f(x) = |x| - 2$ pro x od -4 do 4.
<details>
<summary>Řešení</summary>
```python
def f(x):
return abs(x) - 2
for x in range(-4, 5):
print(f"f({x:2}) = {f(x):2}")
```
</details>
:::
---
## Shrnutí
::: {.callout-note title="Co si zapamatovat"}
- **Funkce** přiřazuje každému vstupu právě jeden výstup
- Zapisujeme $f(x)$ nebo $y = f(x)$
- **Definiční obor** $D_f$ = množina povolených vstupů
- **Obor hodnot** $H_f$ = množina možných výstupů
- **Graf funkce** zobrazuje všechny dvojice (vstup, výstup)
- Funkce je **rostoucí**, když větší x dává větší y
- Funkce je **klesající**, když větší x dává menší y
- V Pythonu definujeme funkce pomocí `def nazev(parametry):`
:::
V další kapitole se podíváme na nejjednodušší typ funkce -- **lineární funkce**, která má přímku jako graf.